含缺陷结构疲劳性能分析方法研究*
2022-07-25赵军峰
赵军峰
(中国直升机设计研究所,江西 景德镇 333001)
0 引 言
随着铸造技术的不断发展进步,新技术条件下的铸造结构兼具高强度、高韧性、高耐磨性等多种优点,铝合金铸件在直升机主减速器、发动机外壳等复杂结构上得到了广泛应用[1-3]。在铸造技术为工程制造带来极大方便的同时,铸造缺陷对结构的使用带来了巨大挑战。铸件的凝固过程通常表现出糊状凝固特性,且共晶凝固温度范围宽,凝固时间长,共晶团数多,铸型壁刚度不足,凝固过程中铸件的膨胀压力大,膨胀力易导致铸型的型壁变形且产生膨胀位移[4]。凝固过程中,早期凝固的固态铸铁容易将合金液分割成许多小的封闭区域,进而使铸件中形成固液共存的不连续熔池[5]。另外,铸件结构多为复杂结构,液态金属在凝固过程中形成较大的温度梯度[6]。多种因素综合作用导致铸件中常常产生铸造缺陷。
铸造缺陷常常存在于复杂铸件结构中液态金属难以补缩的区域及内部最后凝固区域,只有通过先进的探伤技术才能发现,且修复困难。铸造缺陷通常形状不规则,组织不均匀,内含有多个大大小小的不连续缩孔,局部区域的材料组织形态疏松,并且在缺陷铸件表面中所占据的比例(即缺陷率)较大。铸造缺陷对铸件力学性能的影响主要表现在缺陷周边应力分布的不均匀以及应力集中,同时缺陷抗裂性能差,缩短了裂纹的形核寿命,是结构抗疲劳性能的主要威胁之一。
直升机主减速器等复杂结构的加工过程凝聚了非常高的劳动价值,如果不能准确评估缺陷对结构力学性能的影响并对寿命进行预测,将影响设备的使用安全;反之,若过于保守地评估,则会造成巨大的经济损失。因此,研究铸造缺陷对结构力学性能的影响,形成准确的判定依据,既能保证铸造结构设计的安全性和可靠性,又能确保资源的合理有效利用。
笔者从缺陷的形状、尺寸、位置、缺陷类型等特征参数出发,探究缺陷对结构应力分布特性的影响,进一步结合经典Paris- Erdogon公式,基于应力强度因子,反推得到了含缺陷结构的疲劳寿命预测公式,为常用铸造结构疲劳性能的评估提供参考。
1 缺陷对疲劳裂纹萌生特性的影响
在交变载荷的作用下,即使应力幅值远小于材料的屈服强度,在缺陷部位也会产生严重的应力集中。应力集中的直接后果是导致缺陷部位材料出现滑移带,进而形成微观切口[7]。微观缺口的形成进一步加大了铸造缺陷引起的应力集中程度,在某种程度上,微观缺口直接发展为裂纹萌生的缺口,使材料在较小应力水平下发生局部塑性变形,形成裂纹源,而后在循环载荷下进一步扩展。
关于铸造缺陷引起的应力集中情况已有研究,Gao Y X等[8]对铸造铝合金 A356-T6 二维孔洞周围应力集中情况进行了有限元分析。通常认为,缺陷周围的应力集中程度与缺陷的形状、位置等密切相关。
1.1 缺陷形状的影响
缺陷的形状包含了多种不规则形状,然而对于应力集中的影响都可归结到曲率半径上来,曲率半径越小其引起的应力集中越严重。以椭圆形缺陷为例,可以根据其应力的分布解析解式(1)计算得到其椭圆长轴顶端的应力集中程度[9]。
(1)
以椭圆的长/短半轴的比作为椭圆长半轴尖端曲率大小的代表,缺陷的曲率半径对应力集中因子的影响如图1所示。

图1 缺陷长/短半轴比例对应力强度因子的影响
从图1可以看出,随着缺陷曲率半径的减小,缺陷形状更加趋近于裂纹尖端,应力集中程度也急剧增大。
从图2可以看出,MgSO4的加入缩短了固化时间,但粘结强度随之降低。这可能是因为胶黏剂中引入Mg2+,Mg2+会将磷酸二氢铝中部分的Al3+置换形成磷酸二氢镁,在加热过程磷酸二氢镁脱水形成磷酸氢镁,较磷酸二氢铝脱水固化更为容易,故固化速度加快,抗拉强度降低。
1.2 缺陷位置的影响
以半径r圆形缺陷为例,分析孔洞圆心与结构表面间距离对应力集中因子的影响规律,如图2所示。

图2 圆孔对应力分布影响计算模型
以缺陷圆心与表面之间距离D和缺陷半径r的比值D/r来表示缺陷在结构中的相对位置。将其分为几个等级:①D/r≤-1,无缺陷情形;②-1
通过有限元软件建立包含圆形缺陷的无限大薄板模型,提取缺陷外围的最大应力值,与情形①下的平均应力值对比,求得与结构表面之间不同距离所对应的不同应力集中因子,统计分析得到D/r对应力集中因子的影响关系,如图3所示。
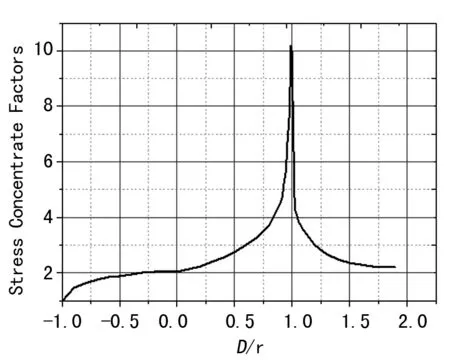
图3 缺陷与表面之间距离对应力集中因子的影响
从图3中可以看出,随着缺陷在结构中所处位置的不同,对应力分布的扰动不同。在缺陷与结构表面距离0.5 关于铸造缺陷的应力强度因子的计算学者们付出了很多的努力,探索出了多种计算缺陷应力强度因子的方法,如引入“等效椭圆”计算缺陷应力强度因子等。众多学者的研究结果表明,缺陷尺寸和位置是影响含缺陷结构疲劳性能的重要参数,计算应力强度因子时需要综合考虑缺陷面积、位置、载荷等多种因素的综合影响。其中,Y. Murakami 的应力强度因子计算模型应用广泛[10],如式(2)所示: ΔK=Kmax-Kmin (2) 式中:α为缺陷位置系数,对于内部缺陷α=0.5,对于表面缺陷α=0.65;Ad为缺陷面积。 对于常用铝合金材料,裂纹扩展寿命与裂纹形核(萌生)寿命分别占整个疲劳寿命的30%~70%左右。然而,对于含缺陷结构,由于应力集中的影响,在疲劳载荷的作用下,裂纹迅速在缺陷敏感部位形核并发生扩展,当疲劳裂纹萌生于缺陷部位且缺陷尺寸较大时,缺陷快速形成一定长度和一定数量的裂纹。并且裂纹形核寿命只占疲劳总寿命中很小的一部分,可以忽略不计, 疲劳寿命主要为裂纹扩展的寿命[11]。 当裂纹形核后,裂纹扩展很快进入长裂纹扩展阶段,裂纹扩展驱动力可以用裂纹扩展速率(da/dN) 来描述, 对于长裂纹扩展, 通常运用线弹性断裂力学的方法与应力强度因子K建立联系, 有著名的Paris- Erdogon 公式[12]: (3) 式中:a是裂纹长度;N是循环周次数;C和m均为材料常数。 根据断裂力学,裂纹顶端附近区域内某一点的位置一旦确定,则应力强度因子KI为该点处的应力、位移以及应变的唯一控制参量,裂纹尖端的应力状态完全由该点处的应力强度因子决定。因此,可以根据应力强度因子及断裂韧性建立材料的断裂判据,即KΙ 在循环载荷作用下,应力强度因子KI通常会随着载荷的变化而变化,其最大值与最小值之间的差值称为应力强度因子变程,用ΔKI表示。随着裂纹尺寸的扩展,应力强度因子不断增大。对同一材料而言,在不同的应力状态下,其断裂韧性是确定的,断裂的发生由断裂条件控制,因为ΔKI=(1-R)KImax,故也可以将ΔKIC=(1-R)KIC作为裂纹失稳扩展的判据[13]。 对于铸造缺陷,由于缺陷为二维或三维特征,而裂纹的长度为一维特征,因此无法从缺陷断口中准确地测量出缺陷尺寸所对应的裂纹长度,需要建立缺陷尺寸与裂纹长度之间的等效关系。假设垂直于载荷方向的面积为Adi的缺陷在铸件疲劳过程中的作用与长度为ai的初始裂纹缺陷相当(即裂纹长度ai为面积Adi的当量初始裂纹长度),那么长度为ai的裂纹与面积为Adi的裂纹应力强度因子值相同。由于已知基于裂纹长度的应力强度因子计算方法,如式(4),因此可以以应力强度因子为中间变量,等效得到缺陷面积Ai对应的等效初始裂纹长度ai。 (4) 式中:Y为形状修正因子;σ为最大应力;a为当量初始裂纹长度;ΔKI为当量裂纹a所对应的应力强度因子。 Paris公式中裂纹的扩展速率通过单个循环裂纹的扩展量da/dN描述,当经过一个应力循环时裂纹从ai扩展到ai+1,则裂纹的扩展速率为ai+1-ai,两个裂纹长度所对应的应力强度因子变程值也分别从KI(i)增长到KI(i+1)。因此,这一过程的裂纹扩展速率同样可用应力强度因子等效地表述为KI(i+1)-KI(i),即以应力强度因子为参量的裂纹扩展速率。基于裂纹长度的裂纹扩展速率和基于应力强度因子的裂纹扩展速率之间的对应关系可通过对式(4)等式两边同时进行微分得到,如式(5)所示: (5) 将其代入到Paris公式中,得到基于应力强度因子的裂纹扩展速率描述公式的表达式: (6) 式中:C为裂纹扩展系数;m为裂纹扩展指数;C和m可通过裂纹扩展试验测得。 当材料在循环应力作用下,裂纹从初始裂纹长度a0扩展到临界裂纹长度ac时,应力强度因子从初始状态下的KI0增长到临界应力强度因子(断裂韧性)KIC。对含缺陷铸件而言,KI0对应的缺陷面积的初始状态Ad0,KIC对应的缺陷面积的断裂临界状态AdC。最后这一过程所经历的循环次数可通过对裂纹扩展公式的积分得到。 KI0(1-m)] (7) 对于已知应力强度因子变程ΔKI的情形,根据ΔKI=(1-R)KI,可将式(7)改写为: ΔKI0(1-m)] (8) 含缺陷结构的疲劳力学性能受到多重因素的影响,其中,缺陷的形状与位置是主要影响因素。建立含缺陷结构疲劳寿命的预测方法需要综合考虑缺陷多个因素的影响。文中所建立的疲劳寿命预测方法考虑了缺陷的位置和尺寸的影响,能够客观反映缺陷关键特征参数对疲劳性能的影响,但在工程使用时仍需经过试验验证和修正。2 应力强度因子
3 缺陷对疲劳裂纹扩展的影响
4 裂纹扩展寿命预测
5 结 语
