借助几何直观解高中解析几何选择填空题的研究

◎赵晓玲

(吉林省实验中学本部高中数学组，吉林 长春 130022)

平面解析几何部分一直是高中数学的难点,学生在解决相关问题时往往会感到困难.平面解析几何的基本思想是通过代数方法研究几何问题.但对于某些小题来说,如果单纯利用代数方法去研究,那么解题过程往往会比较繁杂,容易造成“小题大做”.

直观想象是高中学生数学学习中应培养的六大数学核心素养之一.

直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.

直观想象是发现、提出、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础.

直观想象主要表现为:建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物.

平面解析几何题也是几何题，其自身优势是几何直观，它是培养学生直观想象核心素养的一个很好的载体.学生在解题时如果适当借助几何直观，将会使抽象问题直观化，减少运算量,问题的解决自然会十分便捷.

图1

解法1(代数方法)

设∠AOB=θ，△AOB的面积为S，

设直线l的斜率为k(k<0)，

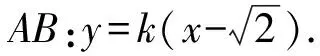
再设A(x1,y1),B(x2,y2)，

∵OA⊥OB，

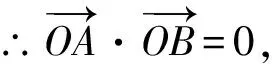
即x1x2+y1y2=0,

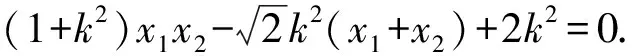
消去y，

解法2(几何方法)

设∠AOB=θ，△AOB的面积为S，

如图2，取弦AB的中点D，连接OD.

图2

由题意得OA=OB=1,

∴∠OCA=30°,

【案例分析】通过两种解法的对比，不难发现，解决圆的有关问题时，适当借助几何直观，不仅方便快捷，减少了运算量，而且更容易理解.此题解法2用到平面几何的两个知识点,它们分别是：(1)圆的垂径定理：垂直于弦的直径平分弦,而且平分弦所对的弧；(2)直角三角形的性质定理：在直角三角形中，如果一条直角边是斜边的一半，那么这条直角边所对的锐角等于30°.

解法1(代数方法)

如图3,设抛物线的准线与x轴交于点K,AB的中点为M,分别过A,B,M向准线作垂线,垂足依次为点C,D,N.

图3

由题意得2p=4,

设A(x1,y1),B(x2,y2)，

∴y1=-3y2, ①

由题意得F(1,0),

设AB:y=k(x-1),k≠0，

消去x,得ky2+4y-4k=0，

y1y2=-4.③

由①②③,得k2=3.

解法2(几何方法)

如图4,设抛物线的准线与x轴交于点K,AB的中点为M,分别过A,B,M向准线作垂线,垂足依次为点C,D,N.

图4

∴|AF|=3|FB|.

设|FB|=a,则|BD|=a,|AF|=3a,

∴|AC|=3a,

由题意得|KF|=2,

【案例分析】通过两种解法的对比，不难发现，解决抛物线的有关问题时，适当借助几何直观，不仅方便快捷，减少了运算量，而且更容易理解.此题解法2用到抛物线的定义和平面几何中的中位线定理.

案例3已知双曲线mx2-y2=1(m>0)的右顶点为A,若该双曲线右支上存在B,C两点使得△ABC为等腰直角三角形,则实数m的值可能是( ).

C.2 D.3

分析双曲线关于x轴对称,若存在B,C两点符合题意,则B,C两点关于x轴对称,故该问题可以转化为过点A且倾斜角为45°的直线与双曲线右支有两个交点.

解法1(代数方法)

此方程有两个不等实根.

①当m=1时,不合题意；

②当m≠1时,

∴0

故选A.

解法2(几何方法)

过点A且倾斜角为45°的直线的斜率为1,

故选A.

【案例分析】通过两种解法的对比，不难发现，该问题可转化为直线与双曲线位置关系的问题.对于直线与双曲线的位置关系的问题,适当借助几何直观,更便于理解,同时也减少了运算量.解法2重点应用了直线与双曲线的位置关系.直线与双曲线的位置关系可以通过比较直线的斜率与双曲线的渐近线的斜率的大小来判断.

通过以上三个案例的解法,不难发现,对于平面解析几何的选择题和填空题的求解,借助几何直观的优势是明显的.因此,教师在平面解析几何的解题教学中要有这样的意识.通过这样的解题教学,学生既能提升数形结合的能力,发展几何直观和空间想象的能力,又能增强运用几何直观和空间想象思考问题的意识，还能形成数学直观思想,进而在具体的情境中感悟事物的本质.对于如何借助几何直观解题,这就需要解题者掌握平面解析几何的基础知识和相关知识,以此为依托,直观想象,数形结合,进而解题.另外,借助几何直观解题也有助于培养学生的直观想象的核心素养.