基于STEM教育理念的高中数学教学实践探索
——以“解三角形”为例
2022-07-25何定彦
◎何定彦
(中山市华侨中学,广东 中山 528400)
STEM是科学、技术、工程和数学四门学科的简称,是美国于20世纪80年代率先提出的教育理念.我国关于STEM教育的研究成果从2003年开始出现,在2016年之后快速增长.STEM教育理念强调多个学科之间的交叉融合,注重跨学科解决实际问题,旨在培养适应现代社会发展的综合型人才.数学是STEM教育的基础工具,STEM教育提供了一个全新的数学教学的视角.在具体的高中数学教学中,它要求数学教师尽量营造一种积极的、活跃的教学氛围,设计真实的问题情境,多提出一些具有挑战性的问题,以此来激发学生的兴趣和探究欲.同时它也要求数学教师应该改变固化的教学经验,把应试教育下的碎片化教学设计整合更新为STEM教育理念下的综合研究型项目式学习.下面以“解三角形”为例,探索如何在高中数学教学中实施STEM教育.

一、授课背景
在新高考的“3+1+2”选科体制下,高中学生的数学水平和能力分层更加明显,尤其是选择物理、化学和生物这种传统理科组合的学生,他们的数学基础相对较好,思维活跃,动手能力和自主学习能力较强,喜欢思考问题和探讨问题,也喜欢利用项目式小组合作的方式解决一些中高难度的综合性问题.在日常教学中,教师要充分考虑学生的性别、性格、兴趣和学习能力等各个方面的不同,将学生分为多个学习小组.项目式小组合作可以培养学生的合作意识,每个学习小组的组员通过不断的磨合,配合得越来越默契,组员之间的指导和督促更加及时和精准,这体现了团队作战的力量.每个学习小组之间以竞争为主,竞争与合作相辅相成,这可以充分激发学生的好胜心和集体荣誉感,使得课堂气氛既紧张又愉快,也让师生关系更加民主.
因为“解三角形”是历年高考的基础考点,是高中数学函数内容的一个重要组成部分,难度系数维持在中低等水平,以选择题、填空题和解答题的形式进行考查,常与平面向量、三角函数、基本不等式等知识点整合,全面考查学生的阅读理解能力、分析问题的能力以及运算能力.对于大部分学生来说,解三角形的题若做得不好或者解题过程中被卡住做得不顺利,不仅仅是这个题目得不到理想的分数,还会在很大程度上影响自己的心态,从而导致后面的题目也做得不好,所以做好解三角形的题非常重要.
在高二数学教学过程中,教师在进行解三角形的章节模块复习时,应该创设综合性较强且有趣的问题情境,以此来激发学生参与探究活动的兴趣,让学生体验发现问题和创造新问题情境的乐趣,进而构建合理高效的课堂教学,培养和提升学生的核心素养和数学思维品质,从而契合STEM教育理念.
二、问题呈现和结果展示
传统的小组合作探究教学模式是教师提出问题后,学习小组开启讨论交流模式,这会导致学习成绩优异的学生或是性格外向的学生主导了整个讨论过程,部分小组成员没有积极地参与整个讨论过程,变成了被动接受者,甚至是附和者,这也是“热热闹闹”的传统小组合作探究教学模式的最大弊端.
为了尽量减少这种情况的出现,教师在课堂上引入例题后,应该限时10分钟,作为每个同学的独立思考演算时间,学生只有经过了充分的自主探究和积极思考,才有可能进入高质量的合作交流.项目式小组合作教学一定要建立在自主探究的基础之上,只有这样,才能为学生提供思想交流、观点碰撞、成果分享的平台.然后再限时10分钟,作为学习小组的交流讨论时间,通过之前的独立思考演算,学生对要研讨的问题有了深入的了解,可以快速地交流各自的思路和想法,进而起到互补和拓宽思路的作用.讨论结束之后限时15分钟,作为结果分享展示时间,每个小组确定第一发言人和第二发言人上台板书或投影讲解本小组的解题思路,这样不仅可以汇报正确的结果和结论,也可以分享错误,或者展示汇报学习感悟.分享展示是检验学生研讨效果的过程,也是学生自我总结提升的过程.最后限时5分钟,由教师进行总结归纳,教师及时中肯的学习评价对学生的发展有积极的导向作用,甚至可能会影响学生的终身发展.积极正面的评价会使学生愿意融入项目式小组合作教学,乐于与其他组员合作,从而变得善于与其他组员合作.
项目式小组合作教学让学生成为课堂的主体,只有让学生充分有效地参与课堂活动,才能有效地实践STEM教育理念.另外,学生十分喜欢这种学习方式,非常积极主动地参与课堂的探究活动.下面是两道例题和小组研讨结果展示.
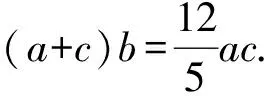
(1)若a,b,c成等差数列,求cosB的值.
(2)是否存在△ABC满足B为直角?若存在,求sinA的值;若不存在,请说明理由.
对于第(1)问,学习小组主要从下面两种思维视角来解答:
1.余弦定理视角
解析因为a,b,c成等差数列,所以2b=a+c.


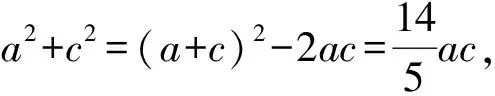
2.等差数列视角
解析由于a,b,c成等差数列,
故设a,c分别为b-d,b+d.


第(2)问是相对较难的存在性问题,学习小组的思维视角更多,下面是归纳整合后的三种主要思维视角:
1.三角函数和正弦定理视角

所以sinC=cosA.


所以(9sin 2A+5)(4sin 2A-5)=0.(*)
又0 所以9sin 2A+5>0,4sin 2A-5<0, 则(9sin 2A+5)(4sin 2A-5)<0,与(*)矛盾, 所以不存在△ABC满足B为直角. 所以sinC=cosA. 所以不存在△ABC满足B为直角. 2.基本不等式视角 所以不存在△ABC满足B为直角. 3.二次方程视角 解析若B为直角,则b2=a2+c2. 即25(a2+c2)2+50(a2+c2)ac-144(ac)2=0 [5(a2+c2)-8ac][5(a2+c2)+18ac]=0, 由于Δ<0,所以方程无解, 所以不存在△ABC满足B为直角. 近年来,随着素质教育的不断深入,人们渐渐认识到数学开放性问题的重要性,数学开放性问题主要有:(1)答案不固定,或者条件不完备的问题;(2)条件多余需选择、条件不足需补充,或者答案不固定的问题.开放性问题可以测试学生的创造能力和水平,不仅能考查学生的素质水平,体现高中数学的灵活性,也能对开放性教学起到良好的导向和推动作用. (1)求B的大小; 请在①AD=DC;②∠DBC=∠DBA;③BD⊥AC这三个条件中选择一个,补充在上面的横线上,并完成解答(如选多个条件作答,按排在最前的解法评分). 对于第(1)问,学习小组的解题方法基本固定,即利用正弦定理边化角,但要注意书写规范,详解如下: 所以sinA>0, 对于第(2)问,学习小组的解题方法各不相同,三个不同的条件从三个角度分别考查了中线、角平分线和高的三种典型解法,都需要先由余弦定理得到: 若选①,BD为△ABC的中线,学习小组呈现出来的三种解题视角: 若选②,BD为△ABC的角平分线. 由S△ABD+S△BCD=S△ABC, 若选③,BD为△ABC的高. 虽然本节数学课只研究讨论了两个例题,但是这两个例题是严格按照高中数学新课程标准的规定来设置的,它们立足于教材和考纲本身,又非常注重考查学生对于基础知识的理解和掌握,也考查学生解决实际应用问题的基本能力和基本方法. 例1的知识点覆盖面比较广,既考查了解三角形中正、余弦定理的综合应用和等差数列中等差中项的性质,又考查了二倍角公式以及诱导公式等知识点.本题可以从多个角度去解答,一题多解.例如从基本不等式、换元思想和二次方程等方向去解答.本题的(1)(2)两个问题的难度设计得有层次也有梯度,第(1)问注重对基础知识的考查和数学思想方法的简单应用,第(2)问对学生的数学思维能力和实际应用能力要求较高,综合性较强,体现了STEM教育理念的整合思想.其中第(1)问难度合理,大部分学生都可以解决,第(2)问难度较大,比较适合项目式小组学习讨论,从而集思广益.从不同的角度去思考和探索问题的规律,是理解知识、解决问题的关键,也是STEM教育的本质. 例2是多条件开放性解答题,与其称其为开放题,不如称其为选做题,因为三个条件一旦选择一个之后就与传统题目一样.当然,有时也会变为三个条件中选择其中两个作为条件,另一个作为结论,进行求解或者证明.这种开放题只是一种试题的呈现形式,它不是难题,要求学生认真审题,理清条件和结论.本题的三个条件从三个角度分别考查了中线、角平分线和高的三种典型解法,是一个不可多得的典型开放式例题,问题涉及的知识面比较广,要求学生能够快速对各类信息进行整合,且不存在唯一的标准答案.这类问题需要学生共同讨论完成,适合项目式小组学习,体现了STEM教育的整合思想. 总体来说,STEM教育的实践探索应注重以下三点:(1)课程设计应该趋于融合,兼顾趣味性和实用性;(2)教学方法应该立足于探究性、自主性和合作性;(3)教育目标应该重视学生的创新性和发展性.这就要求数学教师在平时的教学过程中尽力营造积极、创新、活跃的教学氛围,设计真实的问题情境,多提出一些具有挑战性的问题,以此来激发学生的兴趣和探究欲,同时也要全方位调控,因为在项目式小组学习的过程中,每个小组的学生都有自己的闪光点,学生需要彼此帮助,取长补短,进而确立和培养和谐竞争、合作共赢的意识.

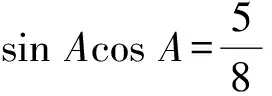
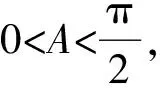
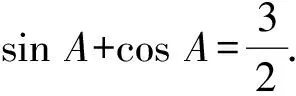
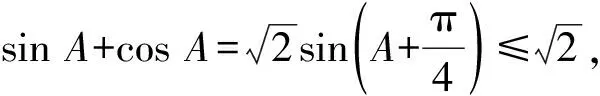



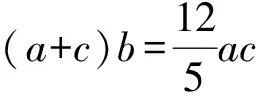





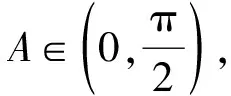






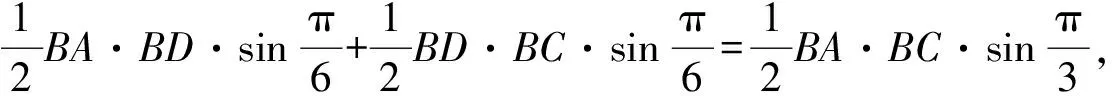

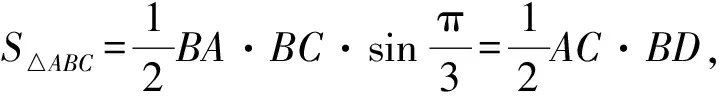

三、总结反思
