两量子比特系统中相互作用对高阶奇异点的影响*

施婷婷 张露丹 张帅宁2)† 张威2)

1) (中国人民大学物理系，北京 100872)

2) (北京量子科学研究院，北京 100193)

1 引言

在具有增益或耗散的开放系统中的简并点，即奇异点(exceptional point，EP)[1]，与厄米体系中的简并点(diabolic point，DP)[2]具有截然不同的性质[3-5]，会产生一系列新奇的现象，如灵敏度增强测量[6-10]、耗散诱导透明或激光[11，12]等，并在量子信息与量子通信、精密测量、光学等多个领域引起了广泛关注.在EP 点处，通常会有两个或者更多的本征值发生简并，同时伴随着本征态的聚合[5，13，14]，使得希尔伯特空间维度降低.而在DP 点，只存在能量的简并，本征态依然可以通过选取合适的幺正变换变成相互正交的，不存在空间维度的损失.当一个量子体系处于简并点时，通常可以通过施加微扰ε破除简并.在DP 点附近，原本简并的本征值发生劈裂，本征值的改变量 Δε正比于微扰的强度，即 与ε呈线性依赖.而 在EP 点附近，Δε正比于ε1/n，其中n是EP 点的阶数，代表有n个本征态聚合于该点.随着阶数n的增大，能量的改变量越显著，即微扰诱导的n阶响应[7，15].因此，在非厄米体系中，EP 点可以实现对微扰更高阶、更灵敏的测量，可用于制作高灵敏度的传感器.高阶EP 点的这一性质可以通过三个相互耦合的光学微腔中的经典光场模式进行模拟演示[7]，而在量子体系中尚未实现.

具有宇称-时间反演(parity-time reversal，PT)对称性的非厄米系统在参数空间中可以实现从全部为实数的本征值到具有互为复共轭的复数本征值的连续调节[16]，即PT 对称性保持相到破缺相的相变，相变点即为体系EP 点.因此，PT 对称的非厄米系统天然具有研究EP 点性质的优势[17].此外，具有PT 对称性的系统已在很多经典体系，如微腔[18，19]、波导[20，21]、电子电路[22，23]等，以及部分量子体系，如超导电路[24]、耗散单光子[25]、冷原子[26]、离子阱[10，27]等体系中得到实现.为了测量EP 点的增强响应，需要精确测量出体系的本征值.在经典体系中，EP 点对微扰响应的强度可以直接通过测量吸收谱的共振峰得到.但在量子体系中，本征值一般无法被直接测量，使得EP 点增强响应的测量具有挑战性.近期，Ding 等[10]在离子阱体系中提出并实现了一种无需拟合任何参数就能直接测定体系的本征值和EP 点位置的方法，且这种方法不依赖于所在的相.这一方案为在量子体系中实现高阶EP 点，并验证其高阶响应提供了新的思路.本文研究了一个具有PT 对称性的全同两量子比特系统，证明了其中存在三阶EP点.通过观测体系的本征值，演示了两量子比特之间的伊辛相互作用可以诱导体系在三阶EP 点出现高阶响应.通过研究体系的本征态，展示了EP 点处态聚合的性质.其次，探究了该体系在PT 对称性破缺相的密度矩阵的性质，并提出利用长时间演化后稳态的密度矩阵验证EP 点处态聚合的方法.此外，根据该体系的三阶EP 点对微扰的响应，基于171Yb+囚禁离子系统中设计了实现和调控EP 点，进而验证三阶响应的实验方案.

2 高阶EP 点处本征值和本征态的特征

考虑一个由两个全同量子比特构成的非厄米体系.每一个量子比特(标记为s=1，2)均由一个具有PT 对称性的二能级哈密顿量描述.其中，J和Γ分别为自旋上下态之间的耦合强度和耗散带来的非厄米项.因此，体系的总哈密顿量同样具有PT 对称性，可写为

这里为2 × 2 的单位矩阵.该哈密顿量满足，其中T=K为复共轭算符，P=σx，1⊗σx，2为宇称算符[10，27].在不考虑扰动的情况下，上述两量子比特体系的PT 哈密顿量的4 个本征值可以通过直接求解久期方程得到，分别为，对应的本征态记为|φ1，2，3，4〉 (见附录A1).当调节参数J和Γ，可以实现前两个本征值从纯实数到互为复共轭的连续变化，即实现了从PT 对称性保持相到破缺相的连续调节.特别地，当J=Γ时，体系对应出现三阶EP 点.此时，所有的本征值聚合到0.其中前三个本征态聚合在一起，如果选择两个量子比特的直积态 {|↑1↑2〉，|↑1↓2〉，|↓1↑2〉，|↓1↓2〉}作为基矢，可以表示 为|φ1〉=|φ2〉=|φ3〉=(-1，-i，-i，1)T.另 外一个与之正交的态为|φ4〉=(0，-1，1，0)T.需要说明的是，这里并未对态进行归一化.在EP 点处，原本为四维的希尔伯特空间塌缩为二维，体系哈密顿量无法被对角化.且在EP 点附近，能量具有更高阶的响应[6，7].

为了研究高阶EP 点处微扰引起的体系能量响应，在体系中引入伊辛型相互作用.其中，Jx为两个量子比特之间的相互作用强度，且满足 0 ≤Jx ≪J.此时，体系的哈密顿量为

图1 微扰作用下高阶EP 点处本征值和本征态的特征 (a)，(b)在高阶EP 点处存在微扰时，体系本征值的实部((a))和虚部((b))随微扰 J x/J 的变化曲线.其中，实线对应本征值的数值结果，虚线代表对 J x/J 做微扰处理后，仅保留最低阶的结果.同一种颜色的曲线对应同一个本征值.(c)本征态|ψ1〉 分别和|ψ2〉 (红色)，|ψ3〉 (黄色)，|ψ4〉 (紫色)的区分度 D1，nFig.1.Eigenvalues and eigenstates near a high-order exceptional point:(a) The real part and (b) imaginary part of the eigenvalues of Hamiltonian Hˆ versus the perturbation J x/J .Here，solid lines are numerical results obtained by direct diagonalization，and dashed lines are those from perturbation.(c) Trace distance between|ψ1〉 and|ψ2〉 (red)，|ψ3〉 (yellow)，|ψ4〉 (purple).

接下来讨论该体系的本征态特征.在量子系统中，迹距离是用来衡量两个量子态距离的物理量，定义为[28]

3 高阶EP 点附近微扰诱导的高阶响应及态聚合的验证

为了展示高阶EP 点对微扰的高阶响应，需要刻画体系的本征值随微扰Jx的变化规律.在由少数量子比特组成的量子体系中，直接测量体系的本征值(本征能量)通常比较困难.此外，在具有相互作用的两比特系统中，对任意初态的演化将和多个本征值有关，其结果将是不同本征值和时间的非线性组合，因此很难像单比特体系中一样通过恰当地选择初态直接测量本征值和EP 点.因此在实验中，一般通过测量某个特定态上占据数的时间演化来间接拟合和本征值相关的参数.为了使实验数据的拟合具有更高的可信度，我们希望尽量准确地确定体系本征值和本征态表达式.但是对于一般的具有相互作用的两量子比特体系，通常无法解析求解本征值，只能通过微扰理论对其进行处理.

在三阶EP 点附近，体系的一个已知本征值为ε4=-Jx，对应的本征态为|ψ4〉=(0，-1，1，0)T.另外3 个本征值满足特征方程

上述本征值的近似结果如图1(a)和图1(b)中虚线所示.可以看出，在Jx很小的情况下，近似结果和数值对角化的结果符合得很好，可以看作是微扰情况下对体系真实能量的较好描述.

同样地，将体系的本征态展开到Jx1/3的二阶，得到本征态的近似表达式为

在这里，下标m的取值范围为m=1，2，3 .由此得到t时刻|↓1↓2〉 上的占据数为

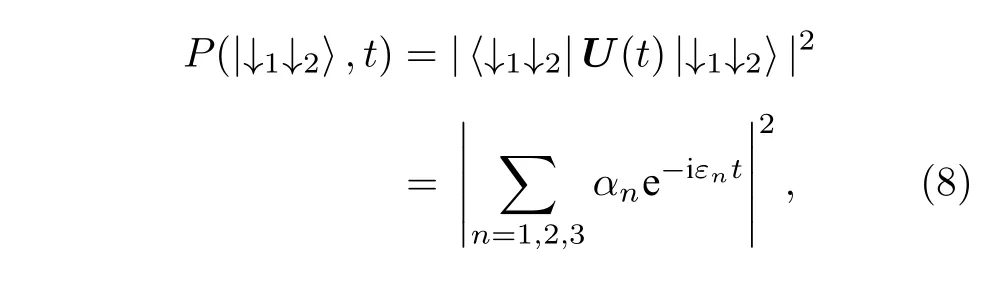
非常重要的是，我们注意到P(|↓1↓2〉，t) 的近似表达式只与J以及前3 个本征值ε1，2，3有关.因此，可以通过占据数的时间演化测量提取出体系的本征值.首先，可以将系统制备在初态|↓1↓2〉 上，在具有伊辛型相互作用的两量子比特哈密顿量的作用下进行演化，并通过荧光探测t时刻该态上占据数.最后通过在|↓1↓2〉 上粒子数随时间变化的表达式拟合出J和本征值ε1，2，3.考虑到3 个本征值之间的关系，在实际处理中可以把本征值的实部和虚部作为独立的参数分开拟合，则只需要拟合4 个实数参数 {J，a，b，c}.通过这一方法，可以测定本征值的实部和虚部对Jx的依赖关系，从而验证EP 点的三阶响应.

此外，EP 的态聚合现象也可以通过测量系统的长时间演化来验证.在非厄米体系中，态的演化通常用密度矩阵来描述[33]，密度矩阵定义为

作为例子，图2(b)—(d)给出了当Jx/J=0.1时，系统从初态|↓1↓2〉 出发演化的结果.图2(b)的子图 分别展示了4 个直积 态|σ1σ2〉 的占据数P(|σ1σ2〉，t) 随时间的变化.其中蓝色点划线和紫色点线分别是|↑1↑2〉和|↓1↓2〉 的占据数演化，红色实线和黄色虚线分别对应|↑1↓2〉和|↓1↑2〉 .这4 个态上的占据数均随时间指数增长，从tJ～5 开始，4 个态上的占据数曲线在对数坐标下斜率相同，但高度不同，说明不同直积态上的占据数比例固定，系统演化到了一个长时间的稳态.图2(b)主图为每个态上归一化的粒子数(|σ1σ2〉，t)=P(|σ1σ2〉，t)/P(t)，其中粒子数.可以清 晰地看出，(|σ1σ2〉，t) 在时间，t) 为t时刻体系的总tJ～5 之后趋于一个常数，说明态演化到了一个不随时间变化的态，即哈密顿量的一个本征态.这是由于在非厄米体系中，系统和环境耦合必然带来信息的交换.在PT 破缺的相中，信息不停地从系统流向环境，因此长时间演化过后，体系会丢失关于初态的全部信息，最终演化到体系的一个本征态上[34].图2(c)和图2(d)给出了演化时间为tJ=10 时密度矩阵的实部和虚部.密度矩阵中的对角项即为4 个直积态上的归一化占据数，与图2(b)主图对应.同时，密度矩阵在演化一段时间后，各矩阵元的大小不再发生变化，也说明了体系处在PT 对称性破缺的相，信息会从体系流向环境，直至丧失初态的全部信息.

图2 系统从初态|↓1↓2〉 演化的量子态布据数结果 (a)从上到下红色和黑色的实线分别代表 J x/J=0.1 和 J x/J=0.01 时，初态|↓1↓2〉 的占据数随时间演化的结果.两条几乎重合的灰色虚线为相应参数下的微扰近似值.(b)主图和子图分别展示了4 个直积态|σ1σ2〉 的归一化占据数和未归一化的占据数随时间的变化.蓝色点划线和紫色点线分别代表|↑1↑2〉 和|↓1↓2〉 的演化，红色实线和 黄色虚线分别对应|↑1↓2〉 和|↓1↑2〉 .(c)，(d)演化时间为 t J=10 时密度 矩阵的实部((c))和虚部((d)).这里选取Jx/J=0.1Fig.2.(a) The evolution of|↓1↓2〉 state population with J x/J=0.1 (red，top) and J x/J=0.01 (black，bottom).The gray lines on the top are the approximate results up to the second order.(b) The evolution of normalized spin product state population|σ1σ2〉 and the corresponding unnormalized populations (inset) with initial state|↓1↓2〉 .From top to bottom，the four lines represent results for states|↓1↓2〉 (purple dotted)，|↑1↓2〉 (red solid)，|↓1↑2〉 (yellow dashed)，and|↑1↑2〉 (blue dot-dashed)，respectively.(c) The real part and (d) the imaginary part of all density matrix elements at t J=10 .For panels (a)—(d)，the coupling strength of Ising interaction is J x/J=0.1 .

4 实验方案设计

实验中利用囚禁在保罗型阱中的171Yb+离子的超精细结构能级来编码量子比特.如图3(a)所示，对于每一个比特，其自旋上下态分别对应171Yb+的2S1/2中的两个超精细态，即|↑〉=|F=1，mF=0〉，|↓〉=|F=0，mF=0〉，它们之间的超精细劈裂能量为ω0=12.6 GHz .此自旋比特系统可以通过多普勒冷却和光泵浦过程实现态的初始化，利用依赖自旋状态的荧光收集来进行量子态的探测和区分.可以将PT 对称的哈密顿量映射到一个纯耗散的两离子系统:首先使用谐振的微波操作耦合每个比特的能级来实现哈密顿量中的自旋翻转部分，其耦合强度J可通过拟合拉比频率测定，并可由通过施加的微波功率来调节大小;然后利用一束370 nm的耗散光实现哈密顿量中的耗散部分，该激光将处于|↑〉 的离子激发到2P1/2态上，处于2P1/2的离子可以自发辐射到2S1/2的3 个塞曼态，并分别放出σ±或π 偏振的光子(图3(a)中的3 个自发跃迁曲线)，最终导致|↑〉态的耗散[34]，其耗散率Γ可以通过耗散光的功率调节.实验系统等效的哈密顿量和(1)式中的两比特PT 对称哈密顿量只相差了一个单位矩阵，即，因此实验上占据数的测量只需乘上一个指数因子 e4Γt即可映射到的结果.

图3 实验方案设计 (a) 171Yb+ 的能级结构及耗散过程;(b) 伊辛相互作用的实现过程;(c)两离子系统中PT 对称的哈密顿量与伊辛相互作用的实现.可以利用微波(黄色)实现自旋态的翻转;利用370 nm 激光(蓝色)实现自旋上态的耗散;利用基于拉曼激光(紫色)操作的MS 门实现伊辛相互作用Fig.3.Experimental scheme:(a) The energy level of 171Yb+ and dissipation process;(b) realization of Ising interaction;(c) realization of P T symmetric Hamiltonian and Ising interaction in a two-ion system:we can use microwave (yellow color) to achieve spin state inversion，shine a 370 nm laser (blue color) to realize dissipation of the spin-up state，and apply Raman laser (purple color)operation for MS gates to implement Ising interaction.

为了实验测量高阶EP 点附近微扰诱导的高阶响应，可以利用离子阱平台中的Mølmer-Sørensen(MS)方案[35]实现两比特操作的伊辛相互作用来施加微扰.该方案基于双光子受激拉曼跃迁过程，利用略微失谐的红蓝边带操作耦合两个离子的自旋比特和声子系统，整个门操作的最小时间和失谐量成倒数关系.同时由于失谐的存在，离子自旋不会向红蓝边带的声子能级跃迁，只会积累一个和自旋初态相关的几何相位.在门操作结束时，自旋系统和声子能够完全解耦，相空间积累的几何相位会产生自旋比特的纠缠，从而实现伊辛相互作用.如图3(b)所示，伊辛相互作用可以通过图中的跃迁路径实现自旋|↓↓〉与|↑↑〉的纠缠，其中n为离子振动的声子能级，红色和蓝色箭头分别为其与相邻声子能级(n-1 和n+1)失谐的红边带和蓝边带跃迁，并且由于失谐的存在，n-1 和n+1 的声子能级在门操作结束时并不会有布居，系统仍处于和初态相同的声子数n，即自旋态和声子态实现解耦.此方案理论上不要求声子初态处于基态上(n=0)，对声子振动能级有很强的鲁棒性.而实际实验过程中，为了对声子有更好的控制，还是可以通过成熟的边带冷却过程将声子初态制备在基态上.另外，|↓↑〉与|↑↓〉的纠缠实现是一样的，只需制备相关的自旋初态即可.实验中可以通过皮秒脉冲激光器产生的双色拉曼光束驱动横向x方向的运动模式，将失谐量设为两个简正运动模式频率的正中间，并实现速度最快的伊辛相互作用操作，其强度Jx可以通过所加红蓝边带激光的强度来调节.

整个实验过程如下:首先通过多普勒冷却，光泵浦过程以及边带冷却将两个离子制备到自旋基态|↓1↓2〉 和声子基态上;然后施加两离子PT 对称的哈密顿量和伊辛相互作用的小扰动，如图3(c)所示，通过调节对应微波和激光的强度来分别控制自旋耦合强度J，耗散率Γ以及扰动大小Jx，使J=Γ和Jx/J=0.1 ;最后通过电子倍增电荷耦合设备(EMCCD)来探测每个离子的荧光，进而得到两个离子的4 个直积态的概率分布.可以记录基态在|↓1↓2〉 随时间演化的占据数，通过在|↓1↓2〉 上粒子数随时间变化的表达式拟合出体系本征值来实验上验证EP 点的三阶响应.同时也可以将系统演化足够长的时间，直至系统处于PT 对称破缺的本征态时，通过单比特门操作改变测量基，实现对两个离子比特的态层析测量，从而得到其对应的密度矩阵，验证本征态的聚合现象.

5 结论

理论模拟并验证了具有PT 对称性的两量子比特系统中存在三阶EP 点，并且两个量子比特间的伊辛相互作用可以诱导三阶EP 点附近能量的三阶响应.其次，探究了该体系在PT 对称性破缺相的密度矩阵的相关性质，发现体系本征态在EP 点存在聚合现象.此外，利用微扰理论研究了该体系的三阶EP 点处能量对微扰的响应，提出了利用基态占据数拟合体系本征值的方法;并利用PT 对称性破缺相的态在长时间演化后会演化到体系的一个本征态上的特性，提出了利用密度矩阵的演化判断EP 点处态聚合的方法.最后，将理论的两量子比特的哈密顿量映射到两离子实验系统中，并基于171Yb+囚禁离子系统设计实现和调控EP 点，验证三阶响应的实验方案.

附录A1 无相互作用两量子比特系统本征值的测量

无相互作用的具有PT 对称性的两量子比特系统可以由正文中(1)式的哈密顿量描述，其本征值的实部和虚部分别如图A1(a)和图A1(b)所示.在该系统中，态的时间演化由演化算符来描述.引入两个物理量PJ和PΓ，它们的时间演化分别为

图A1 无相互作用两量子比特系统的本征值的(a)实部和(b)虚部随耦合强度 J/Γ 的变化Fig.A1.(a) The real and (b) imaginary parts of eigenvalues of a non-interacting two-qubit system as functions of coupling strength J/Γ .

这两个物理量的差值为

当体系处于PT 对称的区域时，ΔP ＞0 ;处于PT 对称性破 缺的区域时，ΔP ＜0 ;在EP点处，ΔP=0 .

附录A2 具有伊辛型相互作用的两量子比特系统中EP 点附近的微扰处理

这部分把两量子比特之间的伊辛相互作用当作微扰，在无相互作用的两量子比特的哈密顿量的三阶EP 点上做微扰展开，保留低阶项，从而得到有相互作用的两量子比特体系的本征值和本征态的近似表达式[7，14].具有伊辛相互作用的两量子比特体系满足的定态本征方程为=ε|ψ〉.哈密顿量Hˆ 本征值所满足的特征方程为

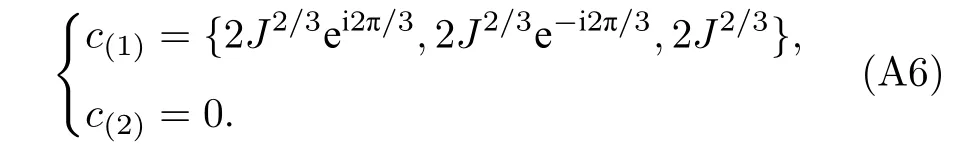
于是，三阶EP 点附近的本征能量的近似表达式为

对于上述提到的本征值满足的三次方程，也可以通过求根公式得到其解析表达式，再对Jx进行展开，保留低阶项.但是对于更高阶的EP 点，高次特征方程的解无法解析得到，因此，这里使用了更为普适的近似方法.图A2(a)和A2(b)分别给出了在对数坐标下本征值的实部和虚部随微扰强度的变化，这里的颜色和线型均与正文图1(a)和图1(b)对应.其中，ε1和ε2的实部和虚部以及ε3的实部对应的曲线的斜率为1/3，说明与Jx呈现三次方根的依赖关系.同时，在图A2(c)和图A2(d)中给出了更大相互作用强度范围Jx/J ∈[0，5] 内，体系本征值的实部和虚部的数值结果.可以看到，在Jx/J更大的区域存在一个二阶EP 点，体系发生从PT 对称性破缺到对称性保持的相变.

图A2 对数坐标系下具有伊辛相互作用的两量子比特体系本征值的(a)实部和(b)虚部的绝对值随相互作用强度 J x/J 的变化.以及在更大的相互作用强度范围内，该体系的本征值的(c)实部和(d)虚部随相互作用强度的变化Fig.A2.The absolute values of (a) the real and (b) imaginary parts of eigenvalues of a two-qubit system with Ising interaction versus the interaction strength J x/J .(c) The real and (d) the imaginary parts of eigenvalues of such a system versus J x/J in an extended range of the interaction strength.

对于该体系的4 个本征态，可以注意到其中一个本征态不随微扰Jx变化，即|ψ4〉=(0，-1，1，0)T.另外3 个本征态满足如下形式

附录A3 PT 对称性破缺相中密度矩阵的含时演化

考虑处于PT 对称性破缺区域的初态|ψ〉，其可被正文中(2)式的哈密顿量的本征态线性展开，即|ψ〉=α1|ψ1〉+α2|ψ2〉+α3|ψ3〉+α4|ψ4〉 .其中|ψ1〉 和|ψ2〉对应的 本征值互为复共轭，记为ε1=a+bi 和ε2=a-bi，并假设b＞0 .另外两个本征值 均为实 数，记为ε3=c和ε4=d.则态|ψ〉的时间演化为

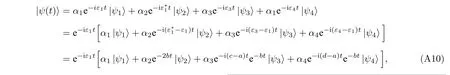
式中后三项均含有随时间衰减的指数因子，在t→+∞时均趋向于零，使得

而初态为ρ(0)=|ψ〉〈ψ|的密度矩阵的长时间演化为

因此，PT 对称性破缺区域的态演化在长时间之后会演化到体系能量虚部为正数的本征态上.