关于氦原子基态能量一级微扰的研究
2022-03-31刘荣
广西物理 2022年3期
刘荣
(广西医科大学玉林校区,广西 玉林 537406)
0 引言
量子力学是研究描述微观粒子结构及其运动规律的学科。物质的电子分布可由它的状态来描述,此状态函数由薛定谔方程决定。对于具有两个以上电子的原子,如氦原子,其状态函数必须同时描述这些的运动规律,要从其对应的薛定谔方程式直接解出,几乎是不可能的事。为此用来处理多电子原子的方法,其中之一就是微扰理论法。多电子体系在一级微扰计算下往往跟实验值相比误差不算特别大,对于求解相应的体系的能量或其他相关参数会取得相对可以接受的结果。
1 微扰理论和计算方法
1.1 非简并定态微扰理论
比较方程两边λ的同次幂项,可得各级近似的方程:
1.2 氦原子基态能量计算
氦原子核外有两个电子。氦原子的哈密顿算符是:
不难看出,电子的能量以及波函数符合:
由以上各式得,C1,C2满足的方程是:
式中决定微扰能量一级修正的久期方程是:
这是单态而非简并。用非简并微扰直接计算能量的一级修正。结果是:
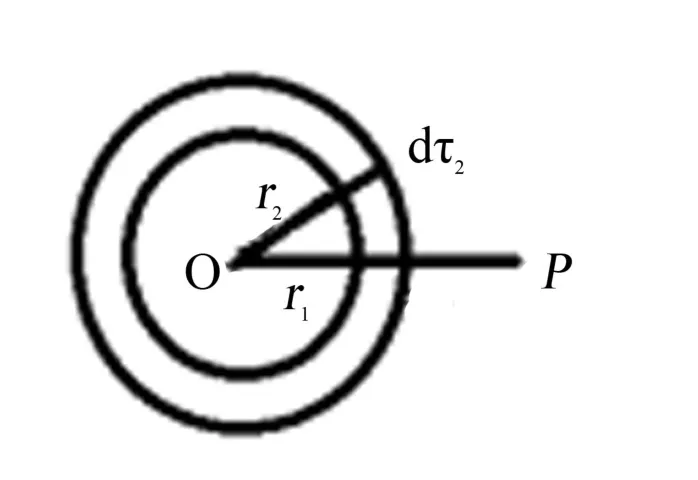
图1 辅助求解的静电势球
代入(14)式中,得到基态能量的一级修正:
于是可以求得一级微扰下的基态能量为:
2 结果和结论
通过上面的一系列的理论推导,我们已经求的一级微扰下的氦原子基态能量为 -74.83eV,而相关研究证实,二级微扰下的氦原子基态能量为-76.1eV,而氦原子基态能量的实际测量值为-78.98eV,为此,通过一级微扰理论所得的计算值的相对误差为:×100%=5.3%。通过本文对氦原子基态能量的一级微扰计算,我们可以推广对于其他多原子基态能量以及激发态能量的计算我们只要计算到一级微扰还是接近实际数值了,二级、三级微扰误差不是很大了,而且三级以上微扰的计算非常复杂,对此我们采取一级微扰基本可以达到解决问题。
