基于类电磁诱导透明的双频段太赫兹超材料的传感和慢光特性*

孙占硕 王鑫 王俊林 樊勃 张宇 冯瑶

(内蒙古大学电子信息工程学院，呼和浩特 010021)

1 引言

电磁诱导透明(electromagnetically induced transparency，EIT)是三能级原子系统中的一种量子干涉现象.量子干涉效应的产生显著降低了被强吸收的特定频率光的吸收率，并在共振吸收区域内产生了一个尖锐的“透射窗口”[1].EIT 现象的产生通常伴随着光的强色散，这显著降低了光速，增强了非线性[2，3].EIT 的早期理论是由Harris 和他的研究团队在1989 年提出，1990 年，该团队首次观察到这种现象[4].自此以后，EIT 效应引起了广泛关注，并被尝试应用于多个领域，如传感器和慢光器件[5-8].然而，原子系统的EIT 现象通常需要在极低温度或高强度的激光下才可实现[9]，这对EIT技术的应用是一个非常严峻的挑战.为了突破这些限制，人们尝试在各种经典系统中实现EIT 现象，如光学微腔[10，11]、滴滤腔波导系统[12]、超材料[13-15].在这个研究过程中，Zhang 和他的团队[16]在2008年使用电磁超材料实现了类电磁诱导透明(electromagnetically induced transparency-like，EITlike).此后，利用超材料获得EIT-like 效应的方法呈现出蓬勃发展的趋势.

目前，利用超材料的各部分结构之间的相互作用来实现EIT-like 效应的方法有两种.一种是超材料中的每一部分都可以被入射的电磁辐射直接激发，并且每部分的共振频率相同或相近.该结构的每个部分称为明模，通过明模之间的耦合，产生EIT-like 窗口[17-21].第二种是在相同的偏振条件下，明模由入射辐射直接激发，暗模由明模的近场耦合激发.EIT-like 效应由暗模和明模之间的耦合产生[22-25].经过对上述两种方法的探索，研究人员通过引入明模或准暗模设计了双频段和多频段的EIT-like 超材料[26-28].这对于超材料在多波段传感器和多波段慢光器件中的应用具有重要意义[29，30].

本文提出了一种新的具有EIT-like 效应的太赫兹超材料.它使用三个明模耦合来产生双频段的EIT-like 效应.通过仿真曲线和电场分布，详细分析了EIT-like 的形成机理.分析了不同折射率和不同厚度的待测物对EIT-like 窗口的影响，研究了超材料的传感特性，确定了被测物质的最佳厚度.对超材料表面覆盖6 种石油产品的情况进行了仿真，仿真结果证明该超材料能进行高灵敏度的物质检测，并进行了待测物的介电常数匹配.显然，双频段超材料的计算结果比单频段超材料的计算结果更接近待测物的介电常数.最后，通过对仿真数据的计算和分析，证明了所设计的太赫兹超材料在慢光效应下也具有良好的性能.

2 结构模型和谐振机理

2.1 结构模型

超材料的谐振层是由周期性沉积在电介质衬底上的图案化金属层组成的.所设计的超材料的金属层包括三组不同形状的结构:双T 型结构(double T-type，DT)、4 个L 型结构(four L-type，FL)和双矩形结构(double rectangles，DR).金属层材料为铜，电导率σ=5.8 × 107S/m，底层介质材料为聚四氟乙烯(polytetrafluoroethylene，PTFE)，介电常数ε=2.1，介电损耗角正切值为0.002.铜层的厚度为2 μm，介质层的厚度为16 μm.该超材料的结构参数如下:l1=120 μm，l2=31 μm，l3=40 μm，l4=49 μm，l5=112 μm，g1=15 μm，g2=5 μm，g3=98 μm，g4=40 μm，w1=10 μm，w2=20 μm.采用三维全波电磁场仿真软件CST Studio Suite 2020 对超材料进行仿真.x轴和y轴方向均设置周期边界条件，在z轴方向设置为开放边界以此来模拟无限周期阵列.将入射光(波矢量k)设置为沿z轴传播的平面波，入射光的电场和磁场分别沿x轴和y轴偏振，如图1 所示.

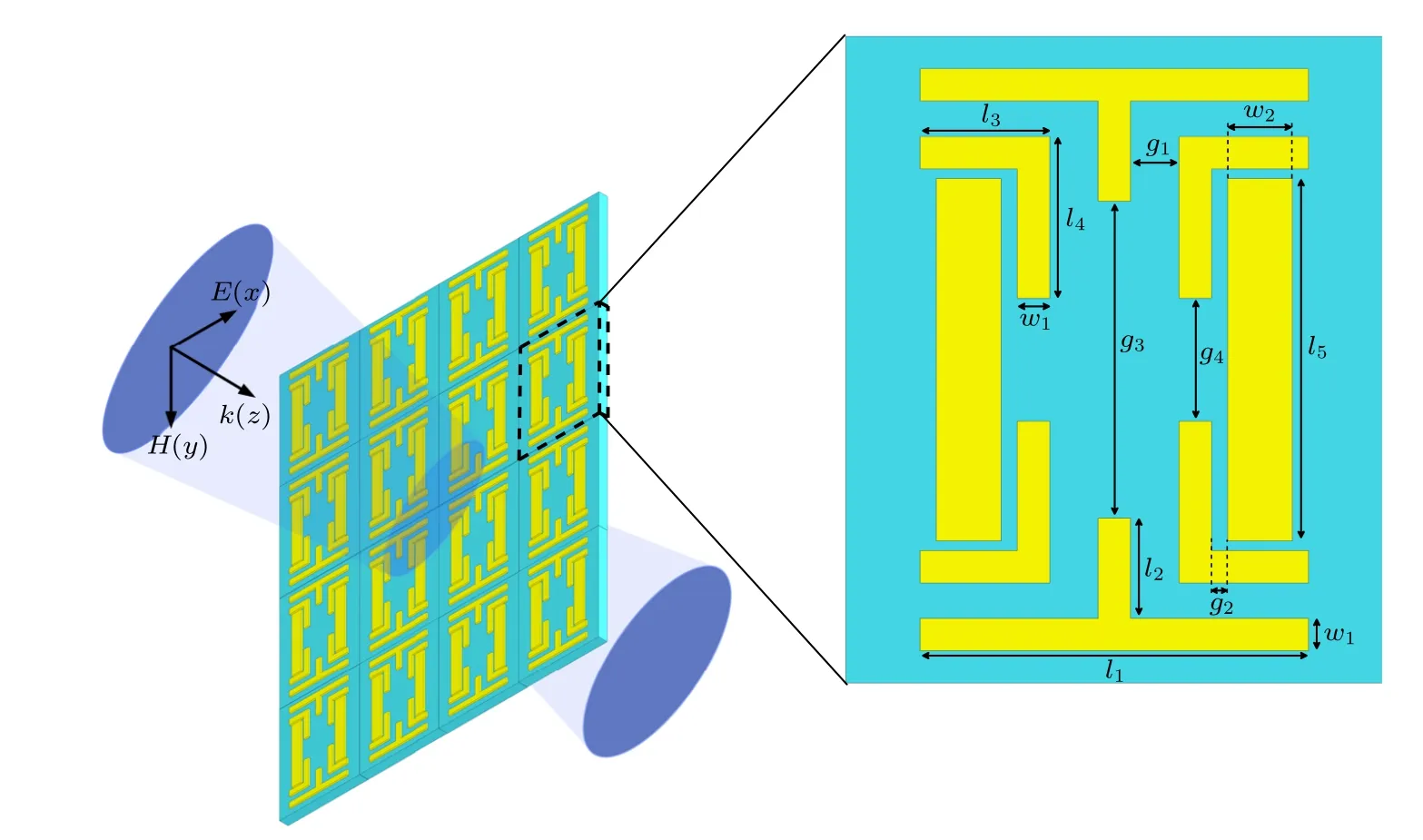
图1 提出的超材料的几何结构和单元结构图Fig.1.Geometry of the proposed metamaterial structure and the unit structure diagram.

2.2 谐振机理分析

一个单频段的EIT-like 超材料(single-band EITlike MM)由DR 和DT 组成，结构参数同上.分别对DR、DT 和single-band EIT-like MM 进行仿真，透射幅值曲线如图2(a)所示.在相同的极化条件下，DR 和DT 分别在1.311 THz 和1.379 THz处产生谐振.两组明模的谐振频率相似，谐振窗口的品质因数明显不同，满足EIT-like 效应产生的必要条件.两组明模的传输幅值曲线相干叠加形成单频段超材料的传输幅值曲线.在1.294 和1.439 THz之间形成EIT-like 透射窗口.峰值频率为1.356 THz，传输峰值振幅为0.785.

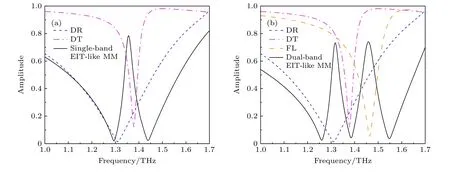
图2 (a) 单波段超材料、DR 和DT 的透射幅值曲线;(b) 双波段超材料、DR、DT 和FL 的透射幅值曲线Fig.2.(a) Transmission amplitude curves of the single-band metamaterial，DR and DT;(b) transmission amplitude curves of the dual-band metamaterial，DR，DT and FL.

EIT-like 透射窗口的物理机理可以利用原子能级系统进行解释，如图3 所示.量子态|0〉 表示原子的基态，|1〉 和|2〉 表示原子的激发态，|3〉 为稳态.入射波可以直接激发单频段超材料的DR 和DT.这个过程对应于原子系统中原子从基态到激发态的转变，可以定义为|0〉-|1〉 和|0〉-|2〉 .由于DR和DT 的结构形式不同，原子系统中原子从基态跃迁到激发态所需的能量也就不同，对应于不同的谐振频率点.在透射窗口的频率点，能量在两个明模之间来回振荡.当振荡能量达到稳定点时，原子系统达到稳定状态，可以定义为|1〉-|2〉-|3〉 或|2〉-|1〉-|3〉 .|1〉 和|2〉 在这个过程中相当于一组相干叠加态(coherent superposition state).通过两条路径到达稳态的原子将产生破坏性干扰，并抑制原子的跃迁.使得原子系统在一定频率下对光的透射率显著增加，出现EIT-like 透射窗口.

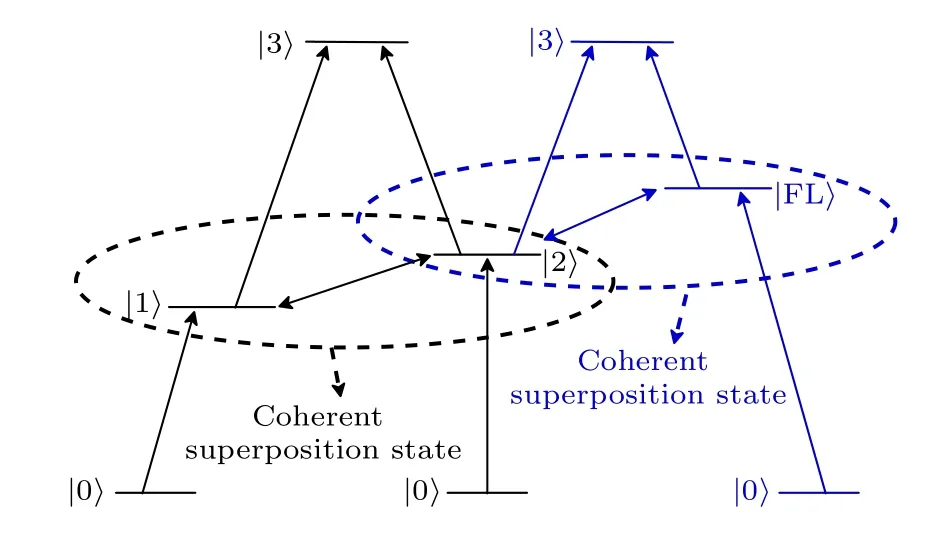
图3 EIT-like 的等效原子能级示意图Fig.3.Schematic diagram of EIT-like equivalent atomic energy level.

通过对原子系统的分析，发现当引入一个新的且合适的激发态|FL〉 后，其与相邻能级的激发态将组合出一组新的相干叠加态，这将大大降低原子系统在另一个频率范围内的光的吸收率，并产生一个新的EIT-like 透射窗口.因此，将谐振频率为1.464 THz 的明模FL 引入到初始的单频段超材料结构中进行仿真，传输幅值曲线如图2(b)所示.各明模透射曲线的相干叠加形成了具有双频段EITlike 的超材料(dual-band EIT-like MM)的透射曲线.两个EIT-like 窗口的峰值频率分别为1.318 和1.459 THz，透射峰的振幅分别为0.733 和0.741.由于各明模之间的谐振差异，EIT-like 窗口的对称性被破坏，透射窗口的波谷频率与每个明模分别仿真的谐振频率略有不同[31].

为进一步揭示双频段超材料的EIT-like 产生机理，详细分析了三个波谷频率与两个透射峰值频率的电场.三个波谷频率的电场分布如图4(a)所示.在波谷频率为1.259 THz 时，入射太赫兹波激发三个明模，但每组明模产生不同强度的电场.此时，电场主要集中在DR 上，其他两组明模激发的电场强度相对较弱.DR 产生电偶极子谐振，DR 与FL 之间的弱耦合使FL 的电偶极子在原电场的力矩作用下旋转，使其电偶极矩转向外电场的方向.因此，FL 上的电场不会集中在L 形结构的两端.在1.385 THz 时，DT 产生电偶极子谐振，DT 的电场在结构中起主导作用.同样，在1.547 THz 时，结构中的FL 激发一个强电场，DT 的电场强度最弱.在图4(b)中透射峰值频率为1.318 THz 的情况下，两个相邻波谷频率处起主导作用的明模之间的弱杂化使得结构的电场强度显著减弱，并导致明显的EIT-like 传输窗口.在透射峰值频率为1.459 THz时，结构的电场强度也显著降低.在靠近透射峰的两个波谷频率处，分别起主导作用的DT 和FL 之间的破坏性干扰产生EIT-like 效应.

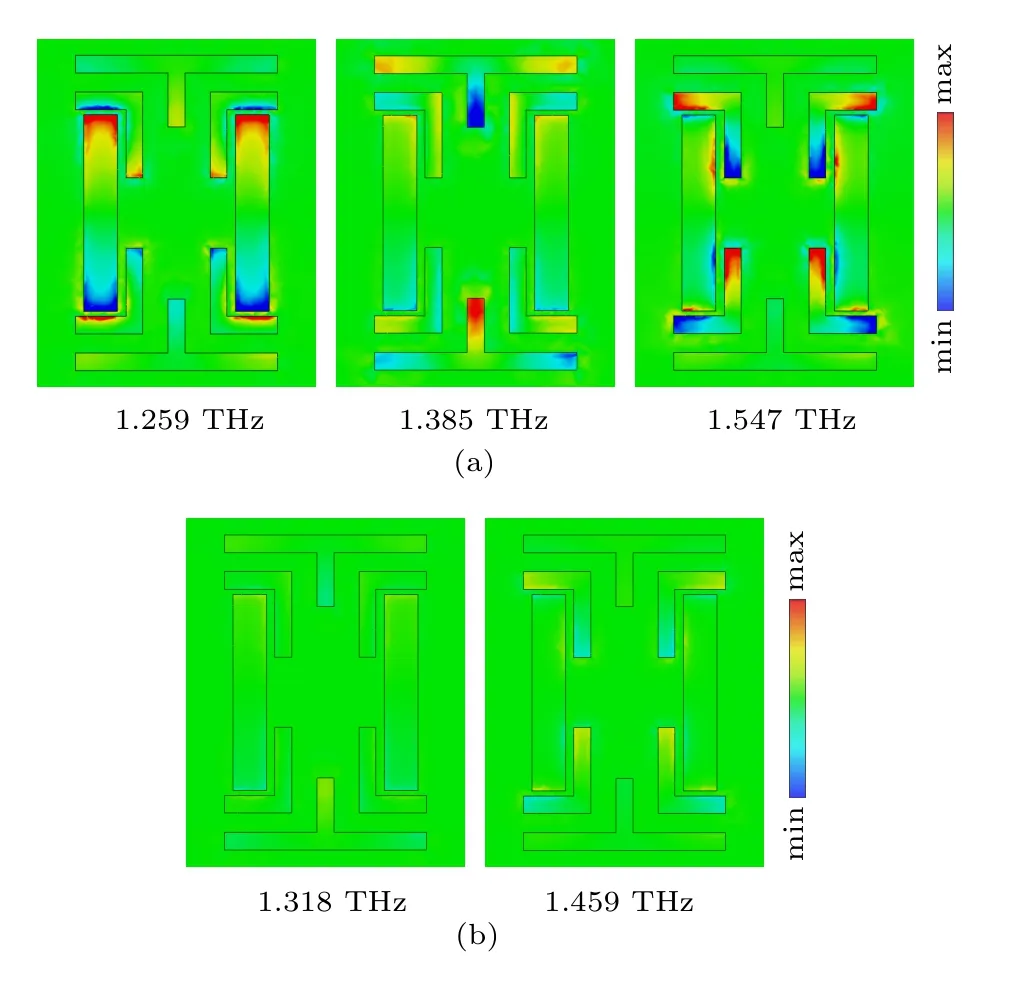
图4 (a) 三个波谷频率的电场分布;(b) 两个透射峰值频率的电场分布Fig.4.(a) Electric field distribution of the three trough frequencies;(b) electric field distribution of two transmission peak frequencies.

3 传感特性

超材料在高频段的共振可等效为等离子体共振[32]，其谐振频率ωp的表达式如下:

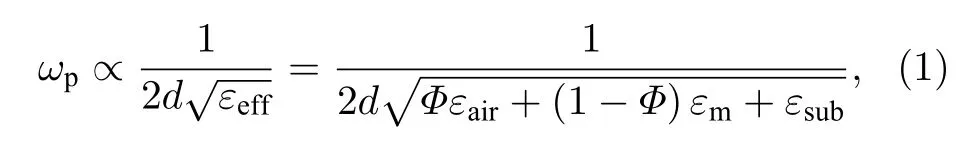
其中，d为超材料单元结构边界尺寸，εeff为超材料周围环境的等效介电常数，εair，εm，εsub分别为空气、超材料表面待测物、基底的介电常数，Φ代表空气在超材料周围环境中所占的比例.当待检测的物质覆盖在超材料的表面，超材料周围环境的空气占比下降，使得周围环境的等效介电常数εeff增大.谐振频率ωp与周围环境的等效介电常数的算数平方根成反比，因此谐振频率向低频偏移.超材料将周围环境的等效介电常数的变化转化为电磁信号的频谱变化，反映在谐振峰位置的移动和超材料谐振特性(品质因数(quality factor，Q)、灵敏度(sensitivity，S)、FOM 值(figure of merit，FOM)等)上，实现待测物质的传感.Q可通过以下公式计算:

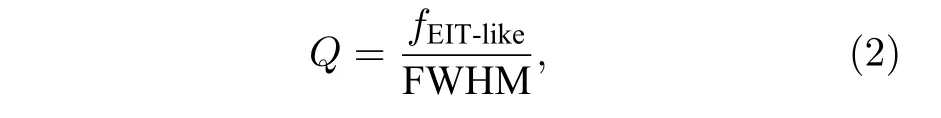
其中，fEIT-like是EIT-like 透射窗口的最大 峰值频率，FWHM 是EIT-like 透射窗口的半高宽.Q反映了传感器的谐振强度和分辨率.S可通过以下公式计算:

其中，Δf为超材料透射幅值曲线的频移量，Δn是超材料表面待测物的折射率变化量.S是单位折射率下的频移变化，即单位折射率下的频移越大，灵敏度越高，传感器对待测物的检测能力就越强.FOM 可通过以下公式计算:

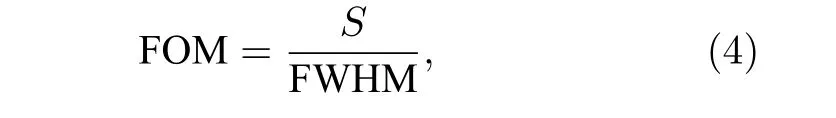
其中，FOM 反映了传感器的整体性能指标.当两传感器的Q和S相近时，更高的FOM 意味着传感器具有更高的整体性能.

对超材料表面覆盖4 μm 厚的不同折射率待测物进行仿真，透射幅值曲线如图5 所示.当覆盖折射率n=1—1.5 的材料时，所有的透射曲线形式不发生改变.随着折射率的增加，EIT-like 峰值频率减小，透射峰的振幅变化不大.两个EIT-like窗口均出现红移，半高宽减小.不同折射率的物质对应不同的透射曲线.因此，所设计的基于EITlike 的太赫兹超材料可以实现物质的传感检测.根据(2)式，未覆盖被测物质的传感器的Q值分别为26.63 和19.46.覆盖4 μm 厚不同折射率的物质后，第一个EIT-like 窗口的Q值在25.29—27.14 之间变化，第二个EIT-like 窗口的Q值在20.15—23.56之间变化.可见，相同厚度被测物质的折射率变化对超材料传感器的Q值影响不大.仿真结果清晰地显示出第二个EIT-like 窗口的频移大于第一个EIT-like 窗口的频移.根据灵敏度的定义，第二个EIT-like 窗口应具有更高的灵敏度.

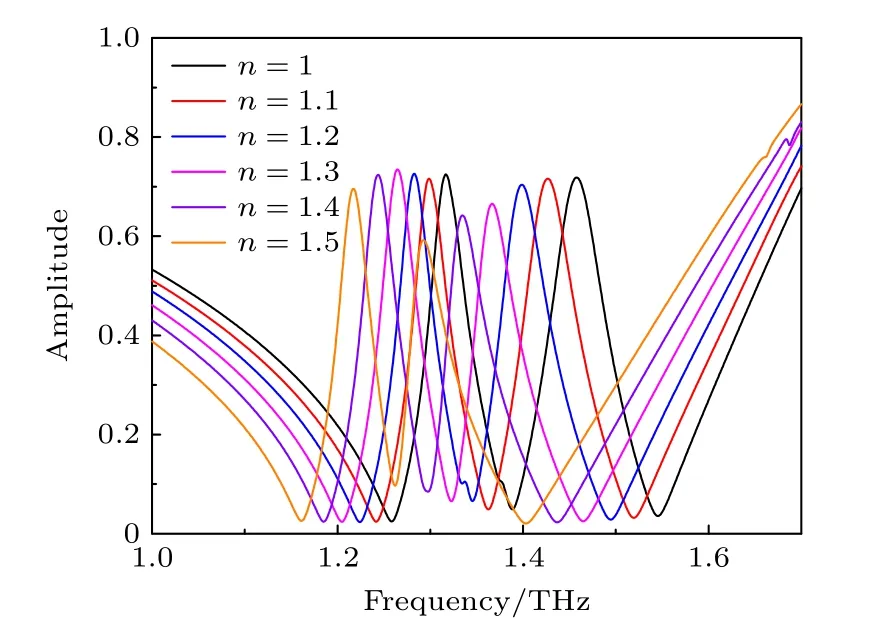
图5 超材料覆盖厚度为4 μm 且折射率不同的被测物的仿真曲线Fig.5.Simulation curves of the metamaterial covered with the measured substances with thickness 4 μm and different refractive indices.

为了研究超材料传感器的折射率灵敏度，根据(3)式确定频移与折射率变化之间的线性关系，即频移量与相应的折射率的线性拟合，拟合直线的斜率为折射率灵敏度.通过上述方法计算传感器的灵敏度.当物质厚度为4 μm 时，两个EIT-like 窗口的灵敏度分别为205.8 和335.6 GHz/RIU.由(4)式可知，随着折射率的增加，第一个EIT-like 窗口的FOM 值在4.05—4.59 之间逐渐增大，第二个EITlike 窗口的FOM 值在4.64—5.93 之间逐渐增大.

基于超材料传感器检测物质的实质，根据麦克斯韦方程组得到频移量与谐振频率之间的关系如下[33]:

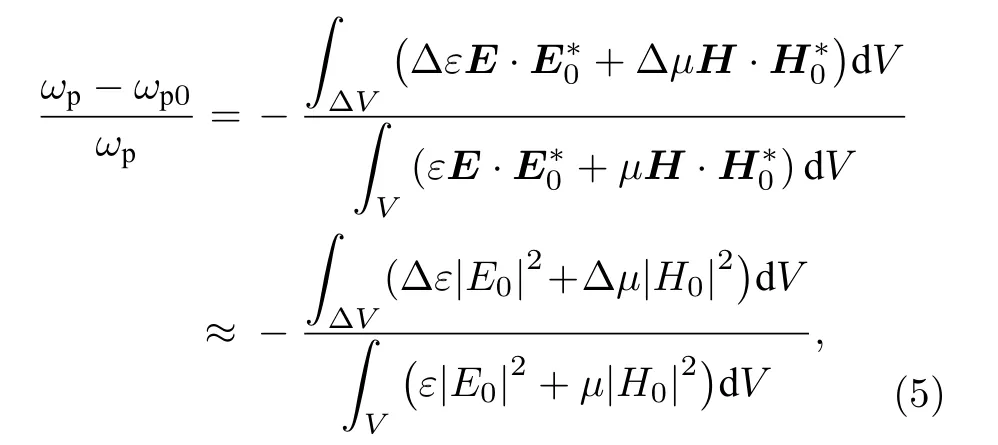
其中，ωp0为未覆盖待测物时的谐振频率，E0和H0为初始场量，ΔV为待测物质体积的变化量，Δε和Δμ分别为介电常数和磁导率的变化量.待测物质改变，Δε和 Δμ改变，产生不同程度的频移，能够实现物质的检测.待测物的体积改变，使得对同一待测物产生不同程度的频移，频移越大，传感器对物质越敏感.而对于覆盖在超材料表面的待测物，底面积一定，待测物体积的变化由待测物的厚度决定.因此，待测物的厚度会影响传感器的折射率灵敏度.将折射率n=1—1.5 且不同厚度的待测物质覆盖在超材料的表面上进行仿真，拟合得到的折射率灵敏度值如图6(a)和图6(b)所示.可以明显看出，被测物质的厚度从2 μm 逐渐增加，拟合线的斜率也逐渐增大.但是，受物质厚度影响的灵敏度增加并不是没有限制.厚度达到30 μm 后，灵敏度的变化趋于减小，如图6(c)所示.厚度为30 μm时的直线拟合程度优于相邻两种厚度时的拟合程度.因此，当物质的厚度为30 μm 时，传感器的灵敏度达到最佳，分别为451.92 和545.31 GHz/RIU，FOM 值分别为4.75 和6.21.综上所述，所设计的基于EIT-like 的太赫兹超材料可以作为物质检测的高灵敏度传感器使用.

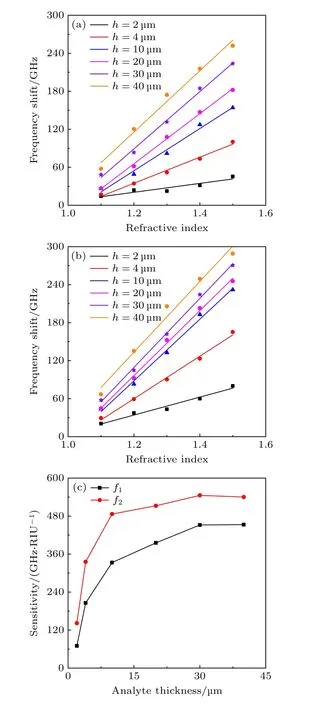
图6 (a) 超材料表面覆盖不同被测物厚度对应的第一个EIT-like 窗口的拟合灵敏度;(b) 超材料表面覆盖不同被测物厚度对应的第二个EIT-like 窗口的拟合灵敏度;(c) 被测物质的厚度对灵敏度的影响Fig.6.(a) Fitting sensitivity of the first EIT-like window corresponding to different measured substances thickness covered on the surface of metamaterial;(b) fitting sensitivity of the second EIT-like window corresponding to different measured substances thickness covered on the surface of metamaterial;(c) influence of thickness of the measured substances on sensitivity.

为进一步验证超材料的传感性能，在超材料表面覆盖介电常数ε 互不相同的喷射推进剂(JP-4)、石油醚(petroleum ether)、传动油(transmission oil)和90 号(90#)、93 号(93#)、97 号(97#)汽油进行仿真.覆盖的石油产品均以最佳厚度进行仿真，以便获得清晰的频率偏移.超材料传感器可以利用峰值频率的偏移来实现物质介电常数的匹配.在不考虑色散的情况下，ε 可通过以下公式估算:

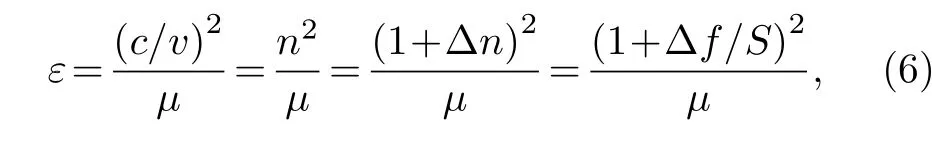
其中，c是真空中的光速，v是光在介质中的传播速度，μ是介质的磁导率(物质为无机材料，μ=1).表1中清晰地显示出，覆盖不同介电常数的待测物对应不同的峰值频率.通过对两个EIT-like 峰值频率的对照，能够在实际传感应用中更加准确地进行物质的检测.有效地解决了单个谐振峰的超材料在应用一个谐振峰值点对物质进行检测时，因受到外界干扰而出现误差，导致物质检测准确性降低这一弊端.利用(6)式对各种石油产品的介电常数进行计算，结果如表1 所列.灵敏度的拟合程度会使得计算的介电常数(calculatedε)与实际的介电常数之间存在误差.利用一个EIT-like 峰的偏移进行物质的介电常数匹配，计算的介电常数与实际存在一些差异.但是，使用双透射峰值频移计算的平均介电常数(calculated averageε)的匹配度要高于基于单峰计算结果的匹配度，使得在物质介电常数的求解中获得更加准确的结果.

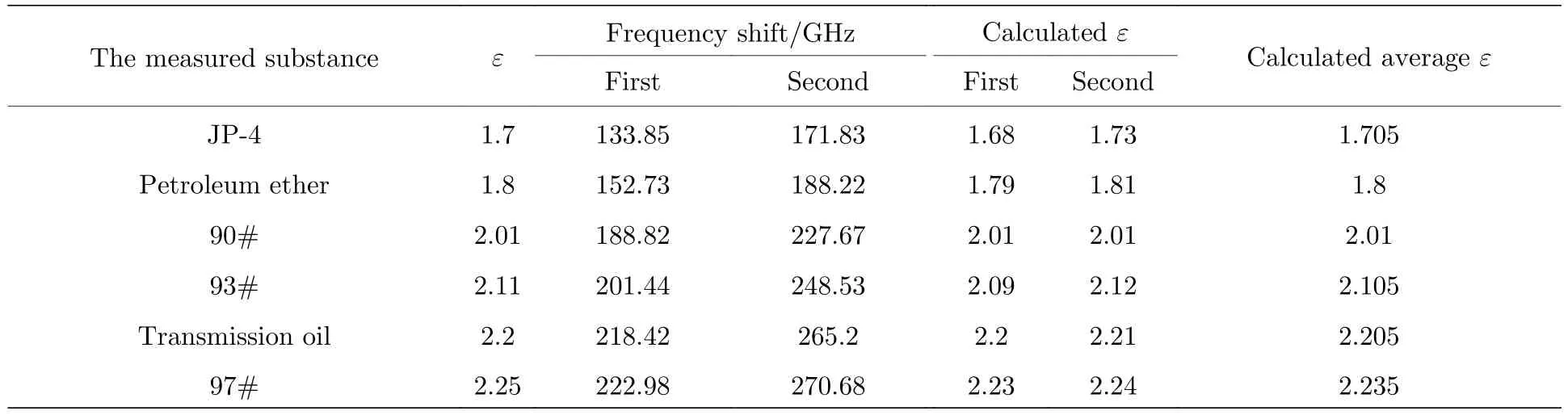
表1 超材料覆盖待测物的仿真和计算结果Table 1.Simulation and calculation results of metamaterial covering the measured substances.

4 慢光特性

EIT-like 的产生通常伴随着慢光效应.群折射率(ng)和群时延(τg)是描述慢光效应的重要性能指标.群时延可通过如下公式进行计算:

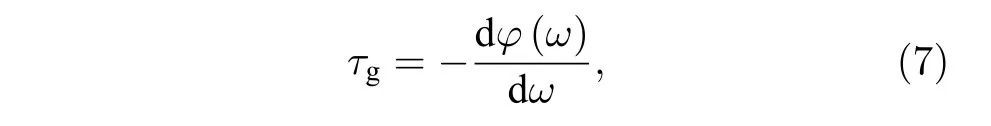
其中，φ(ω) 是太赫兹透射谱中透射相位的相移，ω是相应的频率.群时延代表慢光能力的强度.群折射率计算如下:

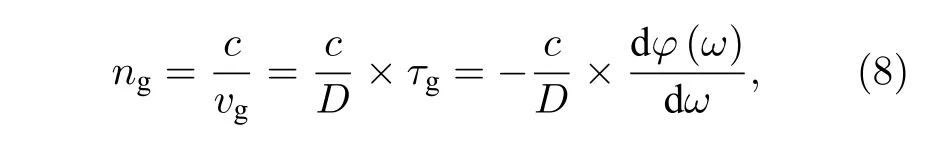
其中，c是真空中的光速，vg是通过超材料的太赫兹波的群速度，τg是群时延，D是超材料的厚度.

从图7(a)中的阴影部分可以看出，EIT-like窗口中的传输相移急剧变化，因此导致透射窗口中的强色散，这与典型的EIT-like 传输特性一致.利用(7)式和(8)式计算群时延和群折射率，结果如图7(b)所示.EIT-like 传输窗口的群时延大于0，具有明显的慢光效应，两个窗口的最大群时延分别达到9.98 和6.23 ps.群时延在透射窗口外为负值，最小值达到—35.87 ps.这并不表示太赫兹波的速度超过光速，导致负延迟区域的传输时间提前，而是振幅包络线无延时通过超材料的现象.本文的群折射率计算方法表明，群折射率与群时延成正比.EIT-like 窗口峰值频率处的群折射率分别达到166.21 和103.75，即太赫兹波通过设计的超材料的传播速度将降低到光速的1/166.21 和1/103.75.综上所述，所设计的EIT-like 超材料在慢光领域具有一定的应用前景.

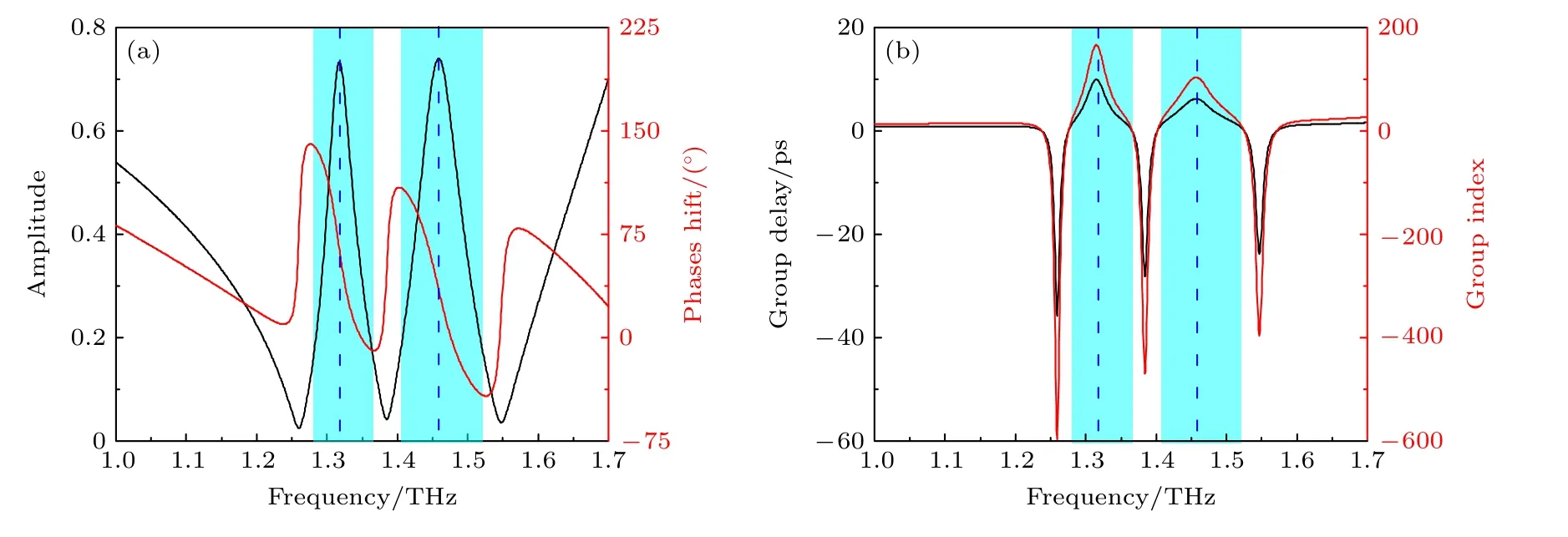
图7 (a) 超材料的传输曲线和相移曲线;(b) 计算的超材料的群时延和群折射率Fig.7.(a) Simulated transmission curve and phase shift curve of the metamaterial;(b) calculated group delay and group index of the metamaterial.

表2 列出了本文设计超材料与当前现有超材料结构的性能比较.在传感方面，所设计的超材料的两个EIT-like 窗口均具有较高的灵敏度，因此，能够实现介电常数相近的物质之间的高灵敏度检测.在慢光方面，实现双频段的慢光效应，群时延最大达到9.98 ps.该结构在传感和慢光领域具有一定的应用价值.

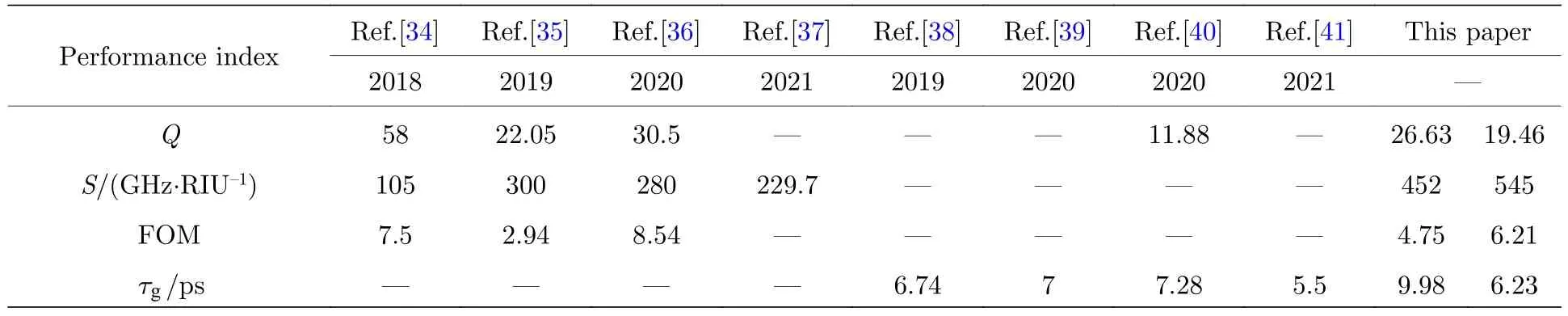
表2 各种超材料在传感和慢光方面性能的比较Table 2.Comparison of sensing and slow light properties of various metamaterials.

5 总结

本文提出了一种具有EIT-like 的双频段太赫兹超材料.超材料单元由三组不同形状的明模组成.仿真得到三个明模透射曲线的相干叠加产生两个EIT-like 透射窗口.结合电场强度的分布解释了超材料的EIT-like 产生机理.根据太赫兹超材料的结构特点和谐振优点，设计的太赫兹超材料可以用作传感器和慢光器件.通过对覆盖不同折射率被测物质的超材料进行仿真，确定了传感器在被测物的最佳厚度下，两透射窗口的灵敏度均超过450 GHz/RIU，实现了低频太赫兹波段内的高灵敏度传感.此外，还利用平均求解的方法解释了双波段超材料与单波段超材料相比在介电常数匹配方面的优势.同时，EIT-like 效应的产生导致在透射窗口中观察到明显的慢光效应，各透射窗口的群时延均大于5 ps，群折射率均大于100，具有良好的慢光特性.提出的太赫兹超材料为实现EITlike 提供了一种策略，对超材料在传感器和慢光器件中的应用具有一定的参考价值.