惩罚策略辅助的快速非支配排序遗传算法Ⅱ研究
2022-07-22王俊艳
王俊艳
(太原科技大学 计算机科学与技术学院, 太原 030024)
0 引言
多目标优化问题是指具有2~3个相互冲突的优化问题。多目标进化算法是一种在解决多目标优化问题方面具有突出表现的一类算法。典型的多目标算法包括快速非支配排序遗传算法(NSGA-Ⅱ)[1],多目标微粒群算法(MOPSO)[2]等。 快速非支配排序遗传算法Ⅱ由于其在解决多目标优化问题上的出色性能,在实际应用中被广泛采用。然而,其采用的锦标赛策略由于存在重复选择具有较高优先级个体的缺陷而导致其多样性交叉以及在某些多目标优化问题上性能表现一般。
针对此问题,许多学者做出了有效地改进。张茂清等[3]提出了基于维度扰动的快速非支配排序遗传算法Ⅱ,即将采用锦标赛策略选择出的个体进行局部扰动操作,以此消除重复个体的现象。汪镭等[4]提出引入多个交叉父代个体的策略,以降低重复选择同一个父代个体的概率。吕琳[5]通过将正态分布引入交叉算子的方式设计了自适应交叉算法,有效消除了重复选择父代个体的现象。王青松等[6]提出混合交叉算子的方法扩展搜索空间和减少重复选择父代个体的概率。赵一霞[7]通过设计循环拥挤度距离的方式有效减少了重复父代的现象。田旭杨等[8]提出引入自适应选择与混合交叉算子,并进一步应用于列车运行多目标优化问题中。赵珍珍等[9]则尝试了将粒子群优化算法的速度更新机制引入算法适应值评价并将种群平均分为多个子种群,并从多个子种群中选择代交叉个体,以此避免重复个体选择问题。Li等[10]则设计了正态分布交叉算子和自适应变异算子的方法消除重复个体,保证算法的多样性。Yang等[11]则综合了正态分布算子、自适应变异算子,以及基于方差的拥挤度距离计算方法进一步提升了算法多样性。Kong等[12]提出3个交叉父代的策略以降低重复选择父代的概率。
不同于上述讨论的方法,本文通过设计一种惩罚机制,将每次通过锦标赛策略选择的个体以优先级自适应降低的方式降低个体下一轮中被选择的概率。基于惩罚策略提出了惩罚策略辅助的快速非支配排序遗传算法Ⅱ (fast non-dominated sorting genetic algorithm Ⅱ assisted by penalty strategy,PNSGA-Ⅱ)。
1 基本概念
1.1 多目标优化问题定义
不失一般性,本文中所解决的多目标优化问题在数学上可表达如下[13]:
minF(X)=min(f1(X),f2(X),…,fm(X))
X=(x1,x2,…,xn)∈Rn
(1)
式中:fm(X)是第m个目标函数,X是具有n维变量的解向量;Rn为决策变量空间。
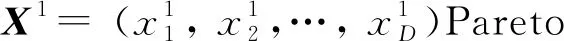
1.2 基本NSGA-Ⅱ介绍
基本NSGA-Ⅱ算法主要包括锦标赛策略、交叉操作、变异操作以及种群更新操作。主要运行过程如图1所示。

图1 NSGA-Ⅱ算法说明
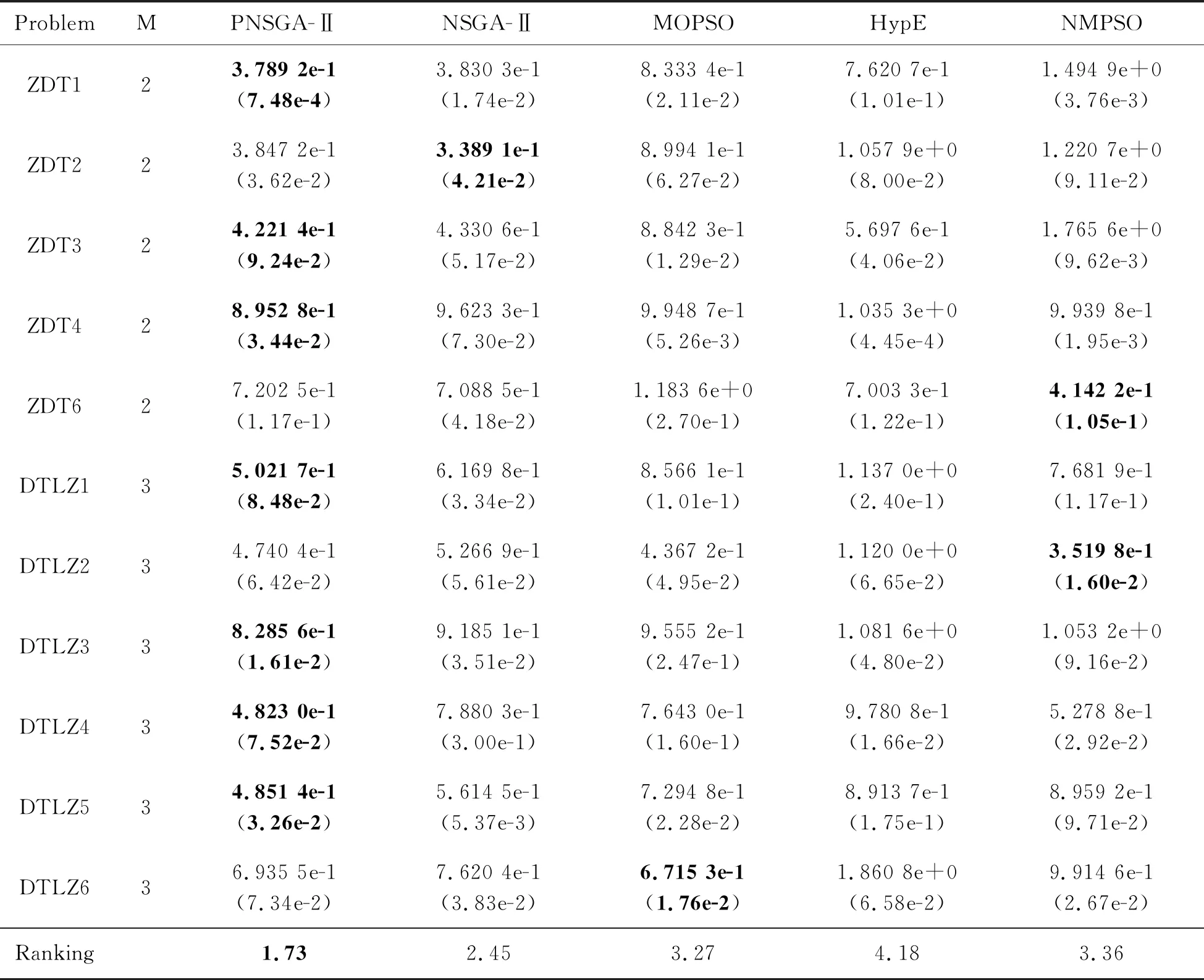
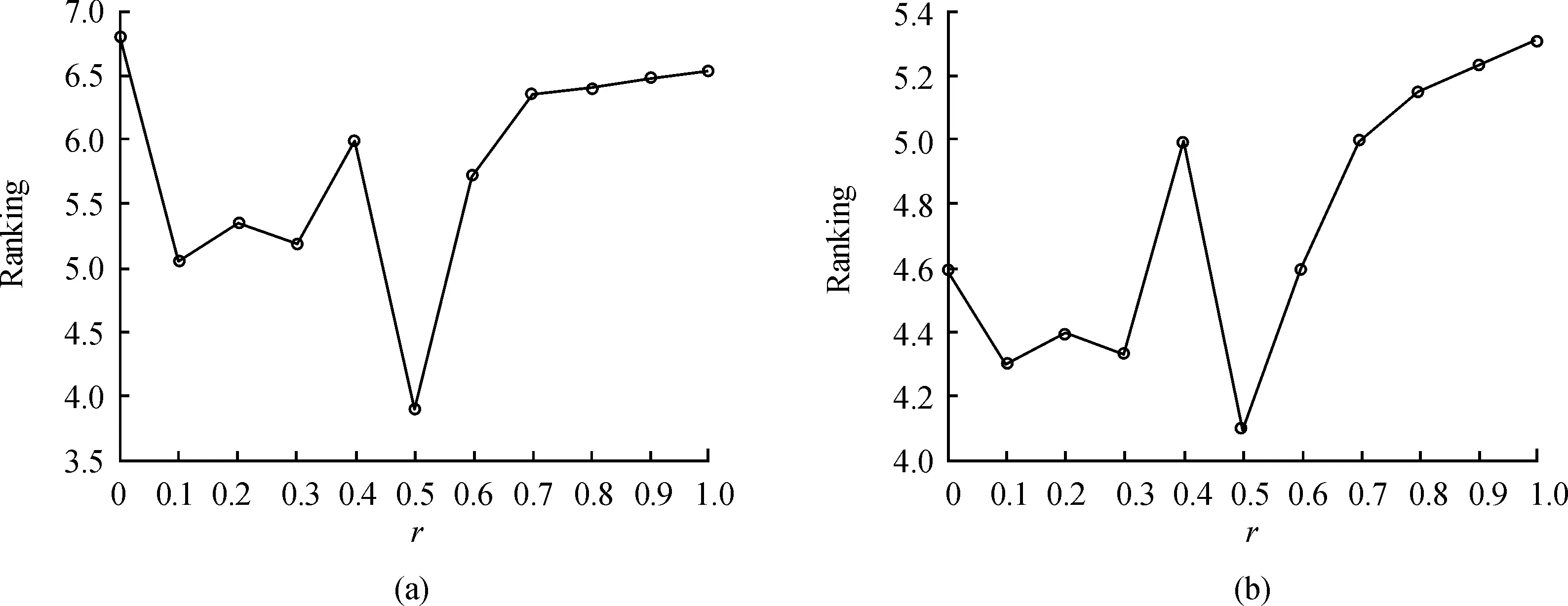
对于第t代具有N个个体的父代种群Pt, 通过锦标赛策略确定待交叉父代个体,然后通过模拟二进制交叉和多项式变异操作产生子代种群Qt;接着,采用快速非支配排序策略对合并的种群Pt∪Qt进行支配分级F1,F2,…。然后,将第1级到第l级内的个体归入子代种群Pt+1=F1∪F2…∪Fl;若此时|Pt+1|=N,则进入下一代循环;若存在|F1∪F2…Fl∪Fl+1|>N和|F1∪F2…Fl| NSGA-Ⅱ中锦标赛策略可表述如下: 1) 确定选择对比个体数,文献[1]中设置为2,交叉池规模为N; 2) 对比选择的2个父代个体所在非支配等级,具有较优前沿面的个体进入交叉池;若两父代个体具有相同非支配等级,对比两个体拥挤度距离,选择拥挤度距离较大的个体进入交叉池; 3) 重复上述1)和2),直到满足交叉池规模。 从锦标赛执行过程可以看出,在第一层非支配前沿面中具有较大拥挤度距离的个体具有更高的优先级。在多次重复执行的过程中,此类个体会被多次选中进入交叉池。虽然这样选择策略有利于保留较优个体的基因,但是不可避免导致后代多样性受到影响。图2统计了锦标赛策略在ZDT1函数上运行一次后个体被重复选择的统计信息,种群个体数为100,实验其他参数设置见实验部分。从图2可以看出,有些个体被多次重复选择3次,5次甚至6次,有6个个体最多被重复选择了6次,说明重复选择同一个个体的现象非常普遍。 图2 重复个体频次统计 针对锦标赛策略存在的重复个体多次被选择缺陷,提出惩罚策略辅助的个体选择机制。主要思想如下:对于父代种群Pt,根据快速非支配排序方法生成多个非支配等级F1,F2,…,Fn。对于个体S∈Fl,其优先级定义为: Os=l+rs/rmax (2) 式中:l为个体S所处非支配等级顺序;rs为Fl中个体拥挤度距离按照降序排列的顺序;rmax为最大顺序。 在锦标赛选择过程中,若个体S被选中一次,则其优先级更新为: Os=Os×er (3) 式中:r为参数,具体设置将在后续实验中讨论。 通过此方式可有效降低个体S在下一轮中被选中的概率。注意,此处个体优先级值越大说明其优先级越低。为清楚表示上述过程,惩罚策略辅助的锦标赛选择策略伪代码如算法1所示,优先级越小的个体对应的Qs越小。 算法1:惩罚策略辅助的锦标赛选择策略伪代码 输入:非支配等级F1,F2,…,Fn,每个个体拥挤度距离 输出:交叉池L 1: ForFi∈{F1,F2,…,Fn} 2: 对Fi中个体按照拥挤度距离大小降序排列 3: 按照式(1)计算每个个体优先级 4: end 5: while |L| 6: 随机选择2个个体S1,S2 7: ifOS1 8:L←L∪{S1} 9:OS1←OS1×er 10: elseOS1≥OS2 11:L←L∪{S2} 12:OS2←OS2×er 13: end 14: end 为了算法完整性,仍然将完整惩罚策略辅助的快速非支配排序遗传算法Ⅱ伪代码呈现,如算法2所示。 算法2:惩罚策略辅助的快速非支配排序遗传算法Ⅱ伪代码 输入:种群规模N 输出:最终种群P 1:P←初始化种群 2: {F1,F2,…,Fn}←执行快速非支配排序策略 3: 计算每个个体拥挤度距离 4: while(满足结束条件?) 5:L←惩罚策略辅助的锦标赛选择方法%如算法1所示 6: 模拟二进制交叉和多项式变异 7: {F1,F2,…,Fn}←执行快速非支配排序策略 8: 计算每个个体拥挤度距离 9:P←环境更新 10: end 为测试PNSGA-Ⅱ的综合性能,采用ZDT和DTLZ[14]测试函数集作为测试用例。所用ZDT测试函数集包括ZDT1、ZDT2、ZDT3、ZDT4和ZDT6。DTLZ测试函数集包括DTLZ1,DTLZ2,DTLZ3,DTLZ4,DTLZ5以及DTLZ6。ZDT测试函数集合中所有函数目标均为2个,DTLZ测试函数集合中所有目标均为3个。ZDT1—ZDT3函数对应的决策变量数目为30,ZDT4以及ZDT6对应决策变量数目为10。DTLZ1函数有7个决策变量,DTLZ2—DTLZ6有12个决策变量。性能指标采用IGD和Spread[15]指标。IGD指标为一类综合指标,不仅可以衡量收敛性,而且可以衡量解集多样性。IGD指标值越小,表明相应算法越优秀。Spread指标用于衡量所求种群多样性。对比算法采用NSGA-Ⅱ[1]、MOPSO[16]、HypE[17]以及NMPSO[18]。对于PNSGA-Ⅱ以及NSGA-Ⅱ,交叉概率设置为1,变异概率设置为1/D,D为决策变量维度。对于MOPSO,每个目标分割数为10。其他参数按照开发者建议设置。PNSGA-Ⅱ中的参数r设置为0.5,具体参数敏感性分析将在实验部分验证。以上所有算法评价次数为10 000次,种群规模为100,每个算法运行20次,并采用Friedman检验方法统计对比实验结果。 表1和表2列出了算法在测试函数上的IGD和Spread指标数据,其中最优值用黑体显示,M表示目标函数维度。最后一行为采用Friedman方法统计出的算法对比结果。从表1可以看出,在所有测试函数上,PNSGA-Ⅱ在8个函数上表现最优。在ZDT4和ZDT6函数上,PNSGA-Ⅱ比NSGA-Ⅱ略差; 在DTLZ3上,PNSGA-Ⅱ整体性能比HypE差。对比标准NSGA-Ⅱ,可以看出PNSGA-Ⅱ在综合性能提升方面较为明显。从表1最后一行Friedman检验结果可以看出,PNSGA-Ⅱ在统计意义上具有最优表现。从表2数据可以看出,PNSGA-Ⅱ在所有算法中仍然表现最优,在7个函数上获得最优值。在ZDT2和ZDT6上,PNSGA-Ⅱ多样性比NSGA-Ⅱ差; 在ZDT6上,NMPSO多样性表现优于PNSGA-Ⅱ;在DTLZ6上,MOPSO多样性表现最好,但是PNSGA-Ⅱ 仍然优于NSGA-Ⅱ。从表2最后一行Friedman统计结果可以看出,在所有对比算法中,PNSGA-Ⅱ整体表现最优。 表1 算法在测试集上的IGD值 表2 算法在测试函数上的Spread值 图3列出了所有算法在DTLZ2上的帕累托前沿面,其中实线表示真实帕累托前沿面,灰色圆点表示算法所求帕累托最优解。从图3可看出,PNSGA-Ⅱ所求帕累托前沿面比较接近真实前沿面,而且分布相对均匀。和PNSGA-Ⅱ相比,NSGA-Ⅱ所求前沿面均匀性较差。如前面分析,从所获得的解集分布性而言,MOPSO表现仍比PNSGA-Ⅱ差。从HypE所求帕累托前沿可以看出,HypE维持种群多样性能力明显比PNSGA-Ⅱ差。NMPSO在收敛性和多样性方面超过了MOPSO和HypE,但是多样性明显比PNSGA-Ⅱ差。从以上分析可以看出,所提PNSGA-Ⅱ整体表现突出。相比于原始锦标赛选择策略,基于惩罚的锦标赛选择策略表现较优。 图3 算法在DTLZ2函数上所求前沿面 为对参数r敏感性做进一步分析,将r分别设置为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7,并在DTLZ和ZDT函数集上对比不同r值对应的Friedman值。算法参数设置如3.1小节所示,结果如图4所示。从图4(a)可以看出,参数r为0~0.3时,有明显下降趋势;r=0.4时,算法性能逐步变差;当r=0.5时,对应算法取得最好性能;当r为0.6~1.0时,对应算法性能逐渐变差。从图4(b)可以看出,当r为0~0.1时,算法性能逐渐变好;当r为0.1~0.3时,算法性能出现波动;当r=0.4时,算法性能明显变差;当r=0.5时,算法取得最好性能;然后随着r增加,算法性能再次变差。从上述2个测试集上的参数r对算法性能影响可以看出,r=0.5时为最优参数,因此选取0.5为最优参数设置。 图4 参数r敏感性分析曲线 锦标赛选择策略是一种在进化算法中被普遍接受的一种选择策略。然而,由于其存在多次重复选择某些优势个体的缺陷,导致算法分布性以及整体性能下降。为解决此问题,提出了惩罚策略辅助的锦标赛选择策略,即将每次所选的个体优先级不断地降低,以此保证在下一轮选择中以较低的概率选择。通过将惩罚策略辅助的锦标赛方法融入NSGA-Ⅱ,提出了惩罚策略辅助的快速非支配排序遗传算法Ⅱ。在ZDT和DTLZ经典测试问题上,实验分析表明了本文中所提惩罚策略的有效性。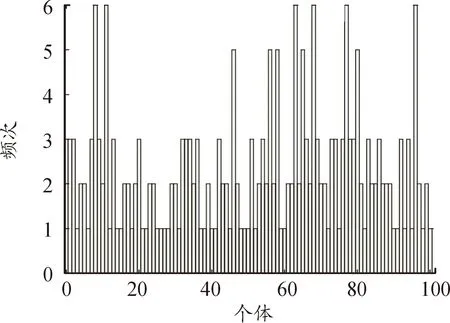
2 惩罚策略辅助的快速非支配排序遗传算法Ⅱ
3 实验结果以及分析
3.1 实验设置
3.2 算法分析


3.3 参数r分析
4 结论
