一种多层经验小波变换与多指标交叉融合的列车轮对轴承故障诊断研究

王大鹏，李 忞，邓飞跃

(1.中车大连机车车辆有限公司， 辽宁 大连 116000；2.石家庄铁道大学 机械工程学院，石家庄 050043)

0 引言

铁路运输是我国交通运输的一个重要组成部分，对保障国家经济发展、人民生活需求具有十分重要的意义。轮对轴承是列车转向架的核心部件之一，其健康状态直接影响车辆的安全运营。由于恶劣的运行工况，列车轮对轴承极易产生各类故障。相对于列车车体、控制系统、轮轨等大型部件运行安全的高度重视，列车轴承的关注度较少，目前仍缺乏较为有效的故障诊断方法[1]。为了降低车辆故障性停机率，避免事故发生，亟待开展有效的列车轮对轴承故障诊断研究。

滚动轴承故障振动信号具有典型的非平稳特征，传统的时域、频域方法无法同时兼顾信号在时频域内的局部化特征。为此，基于时频分解的信号处理方法取得了很大发展[2]，但目前仍存在一些问题有待解决：如短时傅里叶变换(short fourier transform,STFT)只适合分析缓变信号[3]；Wigner-Ville(WVD)分布易产生交叉项干扰[4]；小波变换(wavelet transform,WT)使用固定的基函数，自适应性欠缺[5]；经验模态分解(empirical mode decomposition,EMD)方法可以自适应分解信号获取模态分量，但缺乏完备的数学理论基础，存在模态混叠、端点效应等缺点[6]。

经验小波变换(empirical wavelet transform,EWT)是近年来出现的一种新的时频分解方法[7]，它基于EMD自适应性和小波理论框架，克服了EMD存在的不足，得到了国内外学者广泛应用，李志农等[8]通过EWT分析转子故障信号，识别出了不同程度的碰磨故障；Cao等[9]利用EWT分别提取出滚动轴承单一故障与复合故障特征频率；Kedadouche等[10]则证实EWT方法要优于EMD、EEMD方法，分解模态分量更为准确，效率也更高。

虽然EWT方法具有较好性能，但在实际应用过程中依然存在一些问题：① 传统EWT方法根据频谱局部极值点来划分频谱区间，易受杂频成分干扰，导致信号频谱边界分割并不准确；② 划分信号频谱区间，需要确定故障稀疏度最优的频带范围，虽然已有的峭度、平滑因子、峰度系数等多个统计量指标可以定量评价故障稀疏度的大小，但每个单一指标均存在一定程度的应用局限性[11]。

为解决上述问题，提出了一种基于多层经验小波变换(multi-layer EWT,MLEWT)与多指标交叉融合的列车轮对轴承故障诊断方法。该方法在划分频谱边界过程中，不再以局部极值点作为频谱区间分割的依据，而是通过设定频谱区间个数来对信号频谱进行更为细致的多层分解，同时提出了一种多个统计量指标交叉融合方法来评价、确定信号中故障稀疏度最优的模态分量信号。所提方法可以对信号进行多层次分解，并自适应寻找最优的模态分量信号提取轴承故障特征，通过仿真信号与实验分析，证实了所提方法的有效性。

1 多层经验小波变换(MLEWT)

1.1 传统经验小波变换

给定信号x(t)，其Fourier谱X(f)表示为：

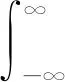
(1)

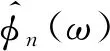
(2)

(3)

原信号可重构为：

(4)

(5)

有关EWT方法的详细过程可参考文献[7]，不再赘述。根据上述过程，可以发现EWT方法中，信号频谱划分区间的个数等于分解后模态分量信号的个数，并且频谱分割后不同区间范围对应以不同紧支撑频率为中心的模态函数。因此，如何分割信号频谱边界直接影响EWT分解的结果。

1.2 MLEWT

受Antoni等[12]所提谱峭度方法的启示，所提的MLEWT方法不再以信号频谱中局部极值点作为频谱区间分割的边界，而是通过设定分解层数，来实现对信号频谱更为细致的多层分解。具体分解过程如下：

1) 设定划分信号频谱的区间个数为k，则整个信号频谱区间[0,π]平均分割为k个连续区间(如图1所示)，表达式如下：

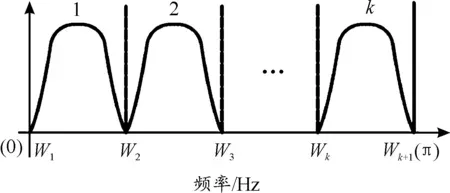
图1 信号频谱划分

(6)

2) 频谱区间划分后，每个区间的频谱带宽表示如下：

B=fs/(2k), (k=2,4,…,N)

(7)

式中：fs为所分析信号的采样频率。通过设置k值大小，能够实现对频谱区间范围的调节，k值越大，信号频谱分割后区间个数越多，对信号频带划分就越细致，最终实现对信号频谱区间的多层划分，如图2所示。

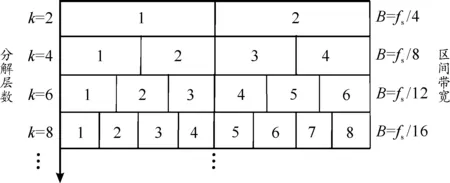
图2 信号频谱多层划分

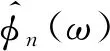
MLEWT方法克服了传统EWT方法根据频谱局部极值点划分频谱区间存在的缺陷，不再受频谱中强背景噪声所引起的大幅值杂频成分的干扰，通过设置k值大小，可以对信号整个频谱区间进行更为灵活、细致的划分。该方法在继承传统EWT方法优势基础上，通过多层分解可以得到多个模态分量信号，进而获取包含故障稀疏度特征最为明显的分量信号。

2 多指标交叉融合

MLEWT方法分解信号后，将会得到多个子分量信号，每个信号对应的频谱区间范围各不相同，因此如何确定区间个数k以及如何选取最优模态分量信号，将是本节所要解决的问题。

2.1 不同统计量评价指标

当滚动轴承出现故障，损伤点与其他元件表面接触时，振动信号会出现瞬态冲击成分，造成信号某些统计量指标发生较为明显的变化。当前应用较为广泛的统计量指标有峭度、平滑因子、稀疏值和峰值系数等。

峭度是描述信号波形尖峰度的一个无量纲参数[13]，数学表达式为：

(8)

式中：u为信号x(t)的均值；σ为信号x(t)的指标值。峭度指标对冲击信号较为敏感，当信号中冲击成分所占比重较多时，峭度值会明显增大，但同时峭度对信号中局部极值点也非常敏感，因此仅采用峭度指标，难免会出现判断失误。

平滑因子表达式为：

(9)

式中：GM(·)为信号x(t)的几何均值；AM(·)为信号x(t)的算术均值。与峭度指标相反，信号中冲击成分越多时，平滑因子越小，并且平滑因子对信号中局部极值不敏感。但是，信号中噪声成分对平滑因子影响较大，导致其可能会无法区分真实的冲击分量和噪声分量[11]。

稀疏值和峰度系数也是常用于评价信号故障稀疏度的统计量指标，它们分别定义如下：

(10)

(11)

式中：RMS(x(t))为根均方函数。

当信号分量中出现故障冲击成分时，稀疏值会明显增大，但文献[14]指出采用稀疏值定量描述信号的冲击性效果欠佳。峰度系数与峭度相似，其数值越大，表明信号中冲击分量越大，但它对冲击成分的敏感度较低，只有出现较为明显的冲击信号时才较为有效。虽然上述每个统计量指标都能在一定程度上评价滚动轴承信号中故障稀疏度的大小，但均存在一定的局限性。

2.2 多指标交叉融合

多指标交叉融合的基本思想是通过选取多个表征信号中故障稀疏度大小的统计量指标，将其融合在一起，综合考虑它们的整体变化情况，克服单一指标存在的缺陷，进而形成一个最终指标，以此确定蕴含故障稀疏度最优的经验模态分量。本文中所提出的融合上述4种指标的多指标交叉融合方法具体步骤如下：

1) 信号经过MLEWT处理后，针对每个固定的k值得到k个模态分量信号，分别计算每个模态分量信号的峭度、平滑因子、稀疏值、峰值系数指标。其中，因为平滑因子数值大小与信号故障稀疏程度成反比，所以取其倒数。将每一类指标作为行向量，构建指标矩阵如下：

(12)

式中：i=k(k=2,3,…,N)。

2) 分别对矩阵中每一类指标进行归一化处理：

(13)

3) 计算矩阵A中每个行向量的Shannon熵值：

(14)

Shannon熵可以较好地评价某一序列的复杂程度，其值大小反映了各个模态分量在同一统计量指标下的概率分布情况。Shannon熵值越小，各分量信号所对应的统计量指标数值彼此越接近，分布越均匀，彼此差别不大；反之，则说明彼此差别较大，出现了个别较为突出的指标值，这代表了某个模态分量信号具有较好的故障稀疏度特征。

4) 计算不同类型指标下总熵值和：

(15)

计算每一类指标对应的权重系数为：

sj=Ej/H(j=1,2,3,4)

(16)

如果通过某一类指标识别出表征故障稀疏度大小最优的模态分量信号，则该类指标的Shannon熵值会较大，相应的权重系数也会较大；如果在该类指标下未找到最优分量，则Shannon熵值较小，权重系数也相对较小。虽然某个统计量指标可能会因为误判导致数值较大，但所选的4个评价指标彼此补充平衡，只有故障稀疏度最优的分量信号所对应的权重系数才能达到整体数值最大。

5) 计算多指标交叉融合后各个模态分量的最终评价指标为：

(17)

取maxC(i),(i=1,2,…,k)对应的分量信号作为信号MLEWT处理后故障稀疏度大小最优的模态分量。上述建立的多指标交叉融合评价方法，综合考虑了4种统计量指标所表征的故障稀疏度大小，避免了单一指标可能造成的误判，有效提高了识别最优模态分量信号的可靠性。所提方法的算法流程如图3所示。

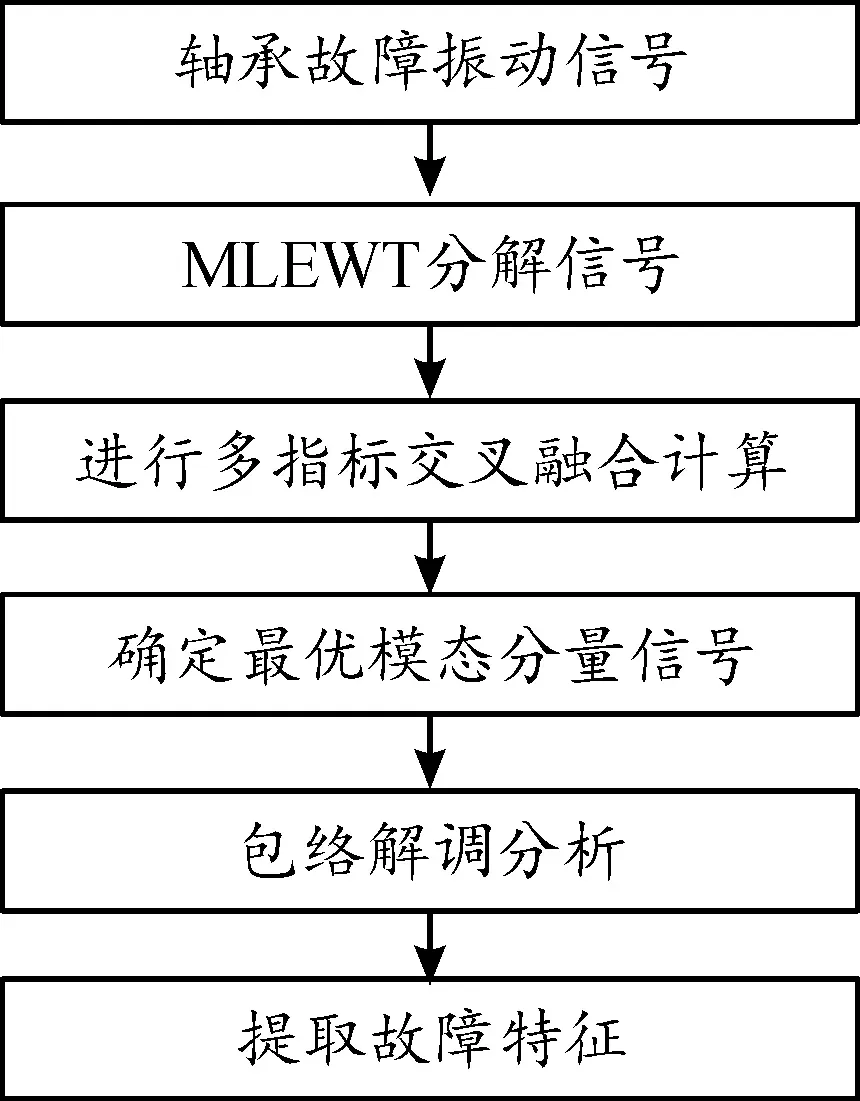
图3 算法流程框图

3 仿真分析

滚动轴承故障仿真信号x(t)包含故障脉冲成分、机械系统其他部件产生的频率成分和高斯白噪声组成的背景噪声成分，数学表达式如下：

x(t)=exp(-1 300t0)(cos(2πf1t))+

0.1sin(2πf2t)+0.15cos(2πf3t)+

xn(t)

(18)

式中：t0=mod(n/fs,fm)，n=0,1,2,…,8 191，采样点长度为8 192，采样频率fs=12 000 Hz，故障特征频率fm=100 Hz。系统载波频率f1=3 500 Hz，其他部件产生的振动频率为f2=130 Hz、f3=430 Hz，xn(t)是添加信噪比为-3 dB的高斯白噪声。

仿真信号的时域波形、频谱及包络谱如图4所示，从时域波形中很难识别周期性的故障脉冲成分；从频谱图中可以看出低频周期性频率成分，但无法识别轴承故障特征频率；包络谱中也无法提取出轴承故障特征频率。根据所提方法，对仿真信号进行MLEWT处理后，对每个分量信号进行多指标交叉融合计算，结果如图5所示。

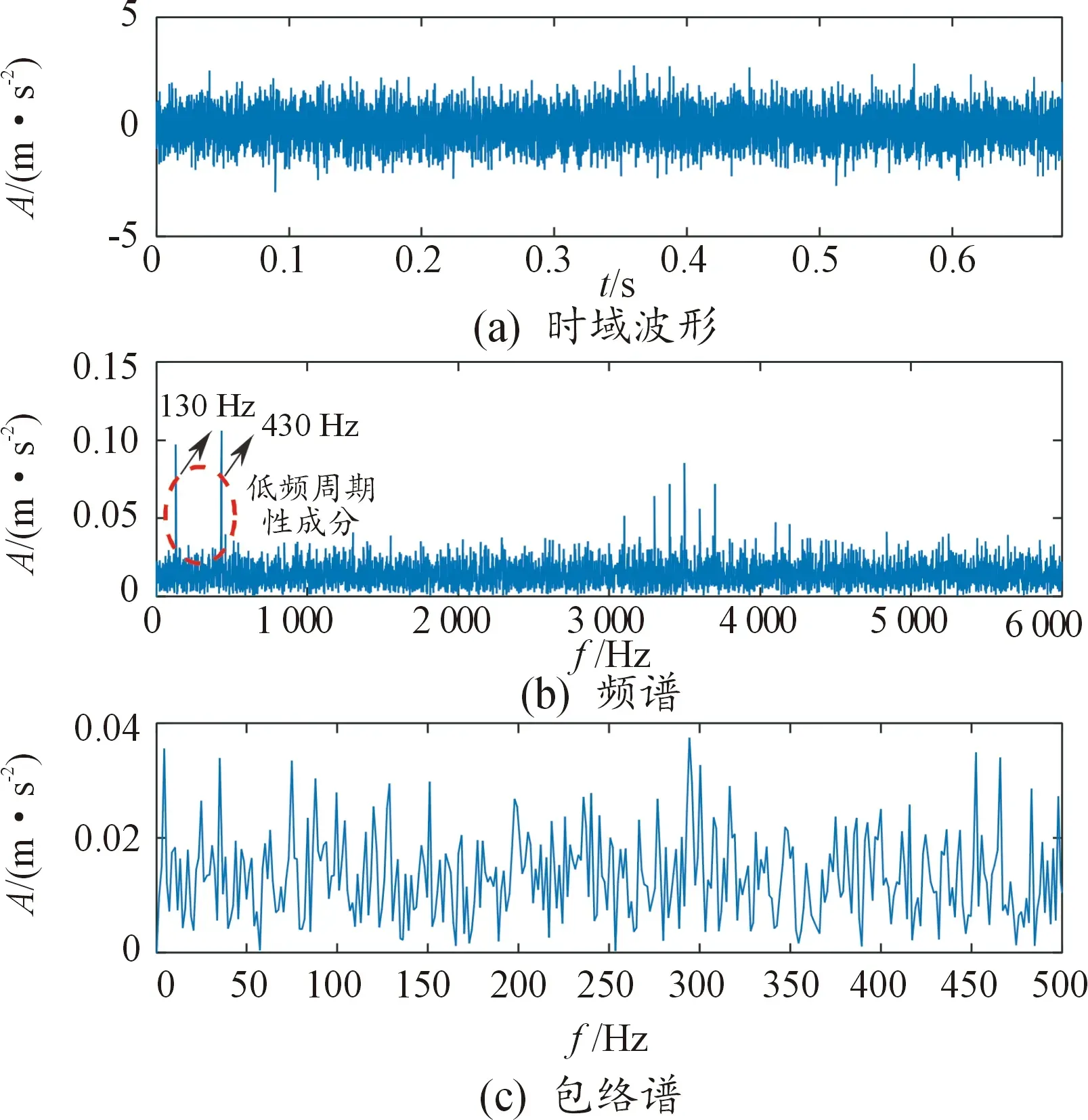
图4 轴承故障仿真信号

从图5中可知，利用所提方法对仿真信号进行了累加的多层分解，通过计算得到的多指标交叉融合最大值对应的区间个数为k=8，选取第4个子信号(红色虚线框内)为最优的模态分量信号。该信号的时域波形及包络解调分析结果如图6所示。从图6中可以清晰地提取出故障特征频率100 Hz及其多倍频成分，这说明通过所提方法，轴承故障特征信息被准确提取出来。

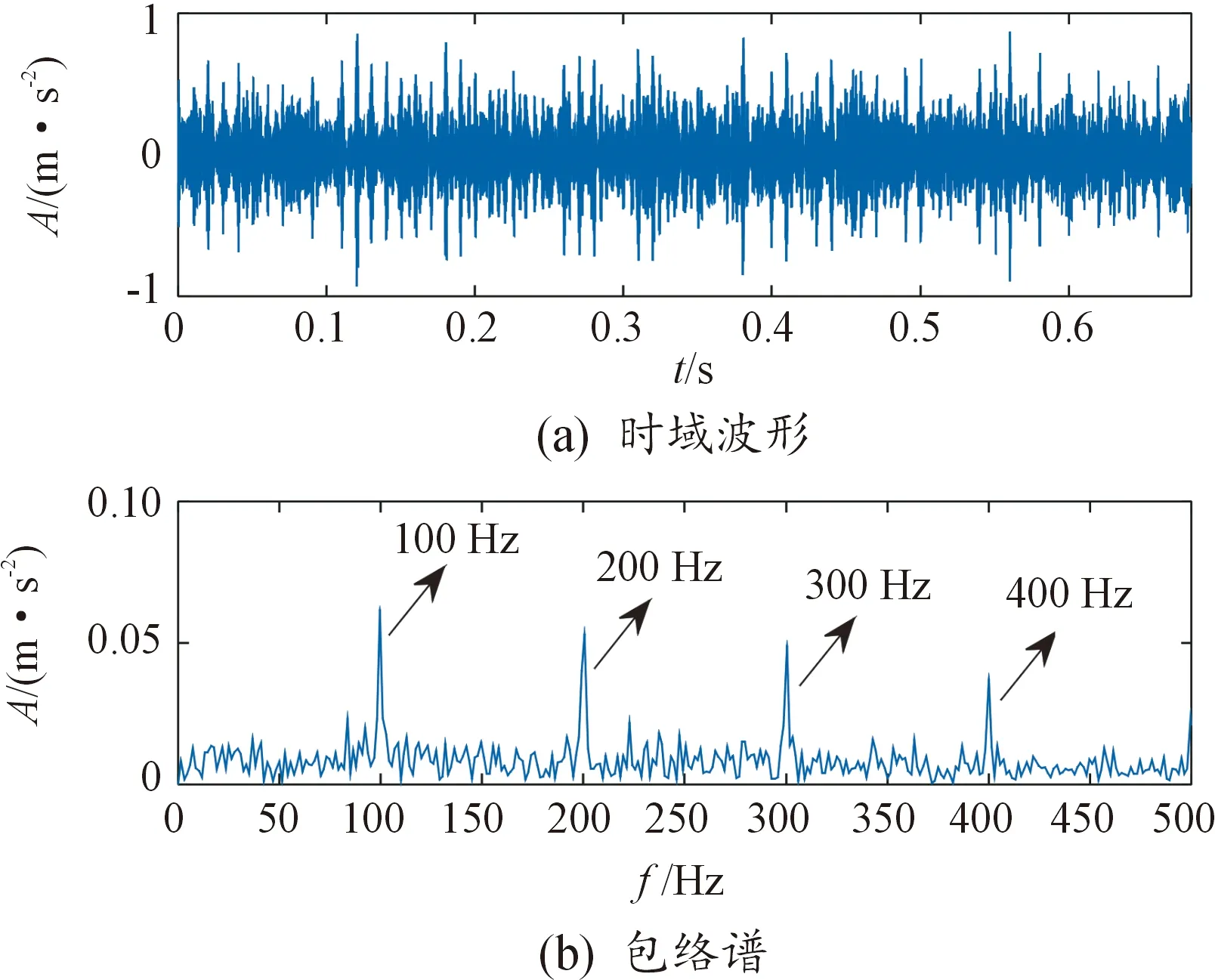
图6 仿真信号故障诊断结果

4 实验分析

实验是在铁道车辆轮对轴承跑合实验台上完成的，测试轴承为双列圆锥滚子轴承，轴承的具体几何参数如表1所示。需要说明的是，测试轴承是从某一型号列车拆卸下来的，轴承在长期使用过程中外圈出现了剥落故障(如图7所示)，此故障为真实的轴承故障形式，并非人为加工。实验过程中，轴承转速为465 r/min，采样频率为12 800 Hz。通过计算，轴承外圈故障特征频率为66.75 Hz。

表1 测试轴承几何参数

图7 测试轴承故障

轮对轴承故障振动信号的时域波形、频谱及其包络谱如图8所示。时域波形中没有发现明显的故障冲击成分，包络谱中也未提取出较为明显的外圈故障特征频率，因此难以诊断该测试轴承出现故障。采用本文方法对该信号进行分析，结果如图9所示，从图9中可知，当划分区间k=12时，最大多指标交叉融合值对应的模态分量信号为第11个(红色虚线框内)。提取该信号进行包络解调分析，结果如图10所示，包络谱中测试轴承外圈缺陷频率及其2、3倍频被清晰地提取了出来，通过该方法可以准确诊断出测试轴承的外圈故障。

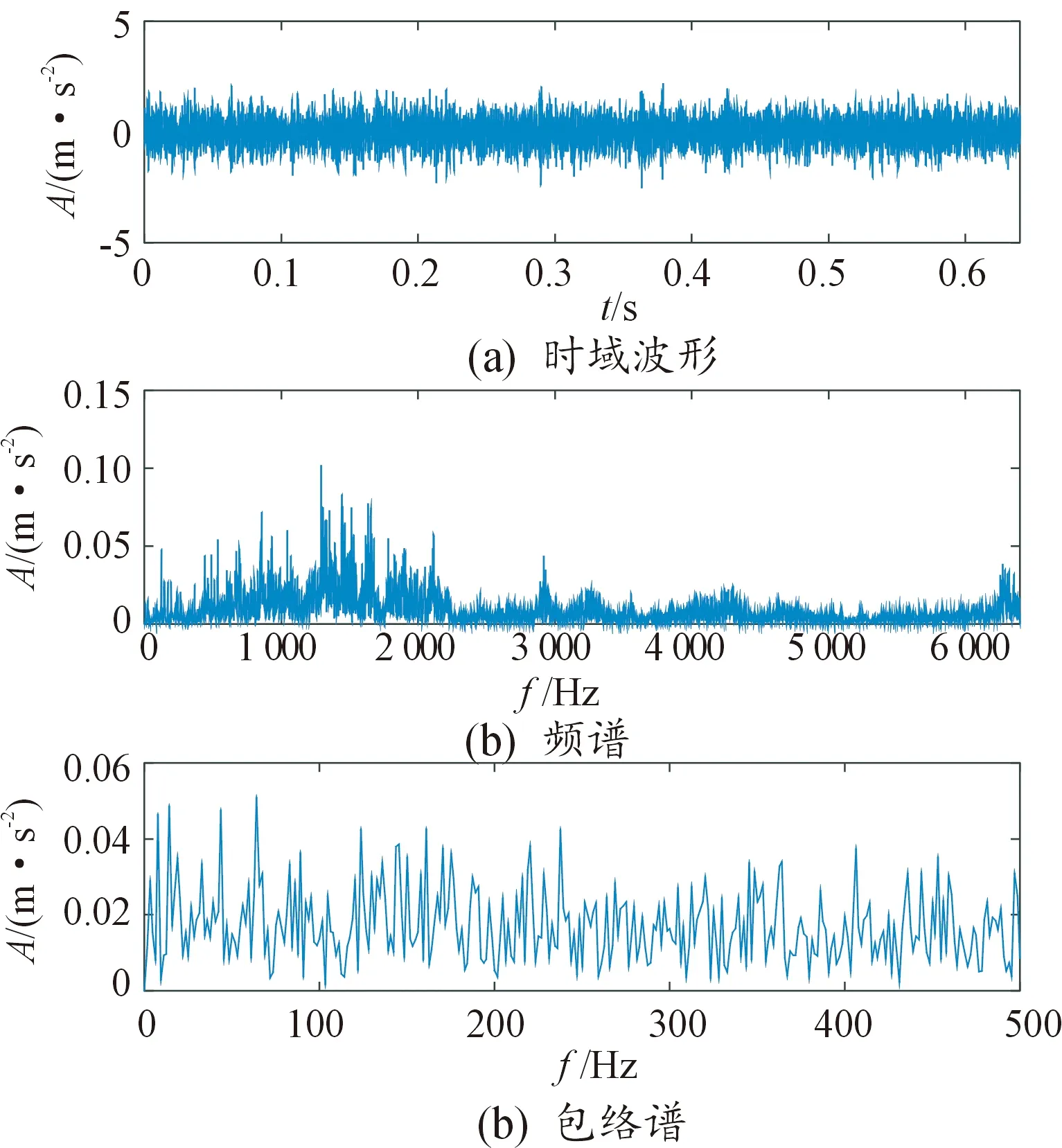
图8 测试轴承信号

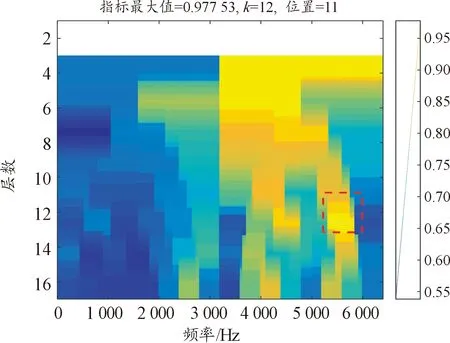
图9 内圈故障信号频谱的分割

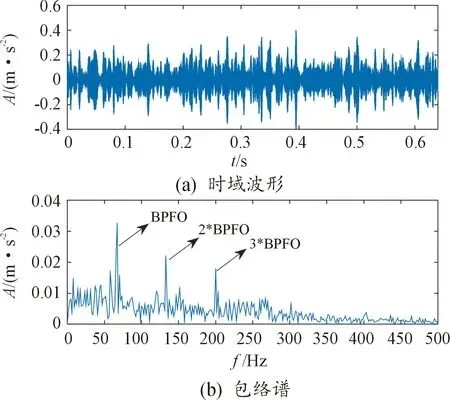
图10 测试轴承故障诊断结果

为了进一步证明所提方法的有效性，采用快速谱峭度方法和传统EWT方法分别分析轮对轴承故障信号与所提方法。快速谱峭度结果如图11所示，最大峭度值对应的中心频率为fc=5 600 Hz，带宽为Bw=1 600 Hz。根据这些参数构建带通滤波器，滤波后信号及其包络谱如图12所示。

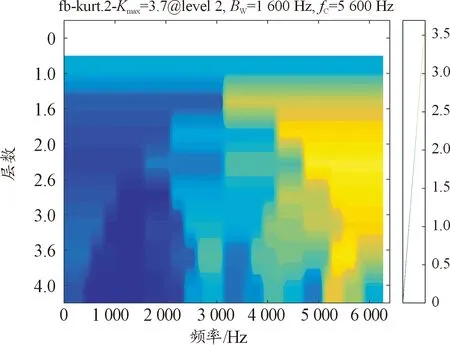
图11 测试轴承快速谱峭度图

图12 测试轴承快速谱峭度诊断结果

从图12中可以发现外圈缺陷频率，但无法提取出故障频率的倍频成分。传统EWT方法中，信号频谱区间分割采用locmaxmin方法，分割的个数为6，结果如图13所示。从图13中可知，由于频谱中杂频的干扰，信号频谱区间的划分主要集中在低频段内，信号的中高频段并未进行有效的分割。选取其中最优模态分量信号进行包络解调分析，结果如图14所示，从图14中可以提取出轴承外圈故障频率，没有明显的倍频成分。通过与图10结果进行对比，可以清楚发现本文中所提方法可以准确提取出轴承故障特征频率及多倍频成分，诊断结果更为可靠，提取轴承故障特征效果更好。

图13 测试轴承EWT结果

图14 测试轴承EWT诊断结果

5 结论

1) MLEWT方法不再以传统EWT方法中根据频谱局部极值点来划分频谱区间，而是通过设定区间个数k，对信号整个频谱区间进行更为灵活的分割。该方法在继承传统EWT方法优势基础上，通过多层分解可以得到多个模态分量信号。

2) 多指标交叉融合方法综合考虑峭度、平滑因子、稀疏值和峰值系数4个统计量指标，通过交叉融合后的最终指标来评价信号中故障稀疏度的大小，克服了采用单一指标引起的误判，并以此自适应搜寻MLEWT后包含故障稀疏特征最明显的模态分量信号。

3) 通过对仿真信号和实测列车轴承故障信号进行分析，证实所提方法能够有效提取轴承故障特征信号，诊断效果优于谱峭度和传统EWT方法，具有一定的工程应用价值。