一种面向智能汽车的工况自适应路径跟踪控制方法

2022-07-22江浩斌韦奇志李傲雪耿国庆

重庆理工大学学报(自然科学) 2022年6期

江浩斌，韦奇志，李傲雪，唐斌，耿国庆

(1.江苏大学汽车与交通工程学院，江苏镇江 212013； 2.江苏大学汽车工程研究院，江苏镇江 212013)

0 引言

智能汽车是一种集环境感知、规划决策、跟踪控制等功能于一体的复杂系统，被视作解决道路安全事故、交通拥堵等问题的理想方案，近年来一直是各国政府、高校以及相关企业的重点研究对象[1]。作为智能汽车的三大核心技术之一，路径跟踪系统的主要功能是根据环境感知以及规划决策模块提供的信息，通过控制车辆转向与速度，沿规划好的参考路径行驶，并保持路径跟踪的精确性和稳定性[2]。目前，针对智能汽车路径跟踪的理论主要有预瞄-跟随理论，比例积分微分(PID)理论、线性最优二次型(LQR)理论、滑膜控制理论、模糊自适应控制理论和模型预测控制(MPC)理论等[3-7]。其中，MPC是基于模型反馈和优化的控制理论，主要由预测模型、滚动优化和反馈校正等部分组成。MPC控制器加入了被控对象的动力学约束条件，是求解复杂系统多目标优化问题的理想方法[8]，近年来被广泛应用于智能汽车路径跟踪控制的研究。

虽然现有的MPC路径跟踪控制器已经能够在很多工况下完成自动驾驶任务，但其在恶劣路面下的路径跟踪控制效果依然不理想。何杰等[9]通过ADAMS/Car实验表明，路面附着系数对行车安全性具有明显影响，车辆在雨雪天和结冰路面条件下，容易失去控制，偏离车道，发生碰撞危险。杨博等[10]提出考虑防碰撞与防侧翻的避障路径规划与跟踪控制，基于MPC理论设计出避障路径跟踪控制器，仿真结果表明，极限工况下车辆LTR值明显增大，跟踪控制效果不佳。辛喆等[11]搭建了基于Carsim/Simulink的联合仿真试验平台，利用YALMIP和GUROBI构建求解MPC问题，在低附着路面工况下，MPC 控制器牺牲了部分路径跟踪的性能以保持车辆的横向稳定性。现有针对智能汽车路径跟踪控制的研究主要是在单一工况的条件下进行的，对于低附着路面、复杂突变道路工况的控制方法研究较少。

为优化MPC控制器在复杂路面条件下的路径跟踪控制效果，笔者提出了一种面向智能汽车的工况自适应路径跟踪控制方法，首先建立三自由度车辆动力学模型，基于模型预测控制原理，设计了智能汽车路径跟踪控制器；然后求取了不同路面附着系数下的路径跟踪最优车速。根据《中国公路路线设计规范》划分了88种典型工况，在传统模型预测控制理论的基础上，利用遗传算法优化得到不同工况下最优时域参数。将纵向车速和道路曲率反馈引入MPC控制器实时匹配最优控制参数，从而实现工况自适应的路径跟踪控制，最后通过Carsim/Simulink平台联合仿真对该方法进行验证。

1 车辆动力学模型的建立

本文主要研究不同道路工况对前轮转向车辆路径跟踪的影响，三自由度车辆动力学模型能够较为准确地反映车辆路径跟踪过程中的横向、纵向、横摆动力学特性，因此，建立简化的三自由度车辆动力学模型作为MPC的预测模型。首先做出如下假设：①车辆行驶于水平路面，忽略侧倾和垂向运动；②将车辆前、后轴简化为单轨，忽略载荷左右转移；③ 轮胎纵向滑移率和侧偏角较小，轮胎力处于线性区。

据此建立的三自由度车辆动力学模型如图1所示。

图1 车辆三自由度动力学模型

图1中，OXY为大地惯性坐标系；oxy为车辆坐标系；a、b为车辆前、后轴到质心的距离；Fx,f、Fx,r为前、后轮沿x轴方向的受力；Fy,f、Fy,r为前、后轮沿y轴方向的受力。

根据牛顿第二定律，将该模型转化为受力平衡方程形式，可得：

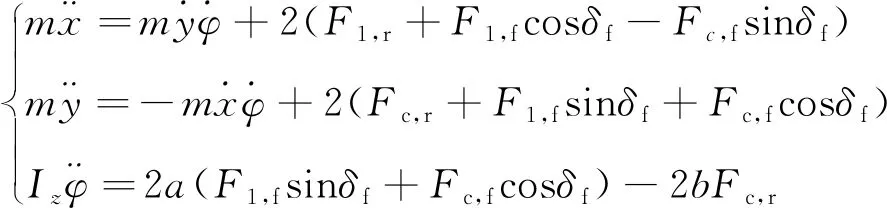
(1)

根据前文假设，车辆前、后轮所受纵向力可简化表示为：

F1,f=Cl,fSf，F1,r=Cl,rSr

(2)

式中：Cl,f、Cl,r为前、后轮纵向刚度，Sf、Sr为前、后轮滑移率。

前、后轮所受侧向力可简化表示为：

(3)

式中：Cc,f、Cc,r为前、后轮侧偏刚度。

将大地惯性坐标系与车辆坐标系之间的关系进行转换，可得：

(4)

联立式(1)—(4)，可得简化后的三自由度车辆动力学模型表达式：

(5)

2 基于MPC的路径跟踪控制器设计

2.1 线性时变模型

车辆在高速行驶时对控制器的实时性要求高，前文所推导的非线性模型难以满足要求，因此将式(5)线性化，得到线性时变状态方程：

(6)

将式(6)采用一阶差商法进行离散化处理，可得：

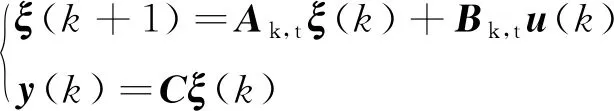
(7)

引入增量模型后的状态空间表达式为：

(8)

式中：Ak,t=I+TAdyn(t)，Bk,t=TBdyn(t)，I为单位矩阵，T为采样周期。

2.2 预测方程

预测方程是MPC控制器的重要组成部分，能根据已有信息和当前输入来预测系统未来的输出。将式(7)转换为：

x(k|t)=[ξ(k|t)u(k-1|t)]T

(9)

得到新的状态空间表达式：

(10)

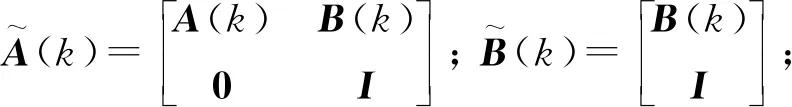
定义k时刻系统输出和输入分别为：

Y(k+1|k)=[y(k+1|k),

y(k+2|k),…,y(k+Np|k)]T

ΔU(k)=[Δu(k|k),Δu(k+1|k),…,

Δu(k+Nc|k)]T

(11)

式中：Np、Nc为系统的时域参数，Np>Nc。

可得系统未来预测方程的表达式：

Y(k+1|k)=ψkξ(k)+ΘΔU(k)

(12)

2.3 约束条件

为了保证基于动力学模型的MPC控制器路径跟踪的稳定性和精确性，需要在控制器的设计中添加车辆动力学约束条件。

1) 质心侧偏角约束

高附着路面约束条件为-10°≤β≤10°；低附着路面约束条件为-2°≤β≤2°。

2) 轮胎侧偏角约束

当轮胎侧偏角≤5°时，为使车辆在低附着路面有良好的行驶稳定性，将轮胎侧偏角限定为-2.5°≤af≤2.5°。

3) 路面附着条件约束

车辆行驶时，侧向加速度与路面附着系数的关系可近似为ay≤μg。为防止系统求解时出现无可行解的情况，将路面附着系数设定为软约束条件ay,min-ε≤ay≤ay,max+ε。

2.4 优化求解及反馈矫正

由于使用了车辆动力学模型，同时也加入了较多约束条件，为减小计算复杂度，提高系统运行效率，故在MPC控制器的目标函数中加入松弛因子，其表达式为：

(13)

式中：Δy(t+i|t)为参考路径和系统输出的差值；Δu(t+i|t)为系统控制增量；Q和R分别为系统输出量和控制增量的权重矩阵；ρ为权重系数，ε为松弛因子。

根据以上目标函数和约束条件，路径跟踪控制器在每个周期内要进行以下优化问题的求解：

(14)

系统在每个控制时域内求解得到控制增量序列：

(15)

将其中的第一个元素作为实际控制增量输入系统，可得：

系统进入下一个控制时域后，不断重复以上过程，以此实现对参考路径的跟踪。至此建立了基于MPC理论的智能汽车路径跟踪控制器。

2.5 车速对MPC跟踪效果的影响

基于MPC原理搭建了Carsim/Simulink联合仿真平台，分析单一路面附着系数下，不同车速对MPC控制器双移线路径跟踪效果的影响。部分车辆参数如表1所示，路面附着系数为0.8。MPC控制器中的预测时域Np和控制时域Nc为固定值，分别设为20、3。

表1 仿真车辆参数

在μ=0.8的双移线仿真工况下，几组不同车速的路径跟踪仿真结果如图2所示。在高附着工况下，MPC控制器对于车速变化具有一定的鲁棒性，速度增加并不会导致车辆稳定性能的明显下降，但单一参数的MPC控制器路径跟踪误差会逐渐增大。这是因为在固定控制参数下，当车速增加时，在相同控制时域内车辆的行驶距离增加，使车辆在各个控制周期内的预测距离增大，从而导致车辆的动态响应性能降低；当道路曲率半径减小时，由于预测时域不变，车辆的路径跟踪精度也会随之降低。

图2 不同车速下路径跟踪仿真效果

3 路面附着系数与最优跟踪车速的关系

3.1 路径跟踪综合评价指标

本文研究的重点是不同路面附着系数下智能汽车自适应路径跟踪控制，因此需要确定车辆在不同路面附着系数下的最优车速。车辆本身是一个复杂的多自由度非线性时变系统，为了更加客观合理地评价车辆路径跟踪中的动态特性，需建立综合评价指标分析不同仿真工况下的智能汽车路径跟踪效果。

郭孔辉教授提出了利用“总方差法”对汽车操纵性能进行有效的评价[12]，本文在该方法的基础上建立了基于操纵稳定性、跟踪精确性、行驶最速性3个方面的路径跟踪综合评价指标。

1) 操纵稳定性评价指标

包括横摆角速度指标:

(16)

侧向加速度指标：

(17)

侧滑危险性指标：

Jl=max(Jl1,Jl2)

(18)

其中，包括前轴侧滑危险性指标：

(19)

后轴侧滑危险性指标：

(20)

取上3项加权平均，得到操纵稳定性评价指标：

(21)

式中：wr1、wr2、wl分别为Jr1、Jr2、Jl对应加权值。

2) 跟踪精确性评价指标

包括侧向偏差指标：

(22)

方向偏差指标：

(23)

取上2项加权平均，得到跟踪精确性评价指标：

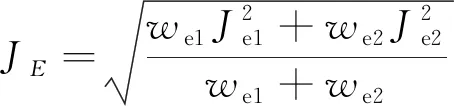
(24)

式中：we1、we2分别为Je1、Je2对应加权值。

3) 行驶最速性评价指标

(25)

4) 路径跟踪综合评价指标

将以上3项指标作加权平方根处理，得到路径跟踪综合评价指标：

(26)

式中：w1、w2、w3分别为JS、JE、JU对应加权值，JC值越小，路径跟踪效果越好。

各项指标的动力学参数阈值和权值的选取参考文献[13]，动力学参数阈值如表2所示。

表2 各项动力学参数阈值

3.2 求解不同路面附着系数下的最优跟踪车速

将路面附着系数从1.0～0.1分成10组进行双移线仿真实验，统计不同车速下，每一组工况仿真过程中的侧向偏差、质心侧偏角、横摆角速度等动力学参数，并计算路径跟踪综合评价指标。

依据路径跟踪综合评价指标JC，计算得到不同μ下评分最优的试验车速集合Vi，如表3所示。可以发现，随着路面附着系数的降低，综合评价最优车速不断减小，这也符合人类在现实道路条件下的驾驶习惯。

表3 综合评价最优车速 km/h

通过5次多项式拟合，得到不同的μ与综合评价最优车速的关系，如图3所示。

图3 路面附着系数与最优车速的拟合关系曲线

4 时域参数自适应路径跟踪控制器

4.1 划分典型弯道工况

传统MPC控制器中的时域参数通常离线确定，且在优化过程中保持恒定，影响了其针对不同工况的鲁棒性，为了提高MPC算法在不同车速以及不同曲率工况下的跟踪精度，需要在MPC控制器中引入纵向车速和道路曲率半径反馈，分析匹配最优控制参数，实现控制参数自适应，从而更加准确地反映智能汽车行驶过程中的动态特性，实现复杂工况下的路径跟踪。

根据《国家公路路线设计规范 JTG D20—2017》，各级公路在设计弯道最小半径时，应与其设计速度相适应。表4为不同设计车速所对应的最小道路曲率半径。

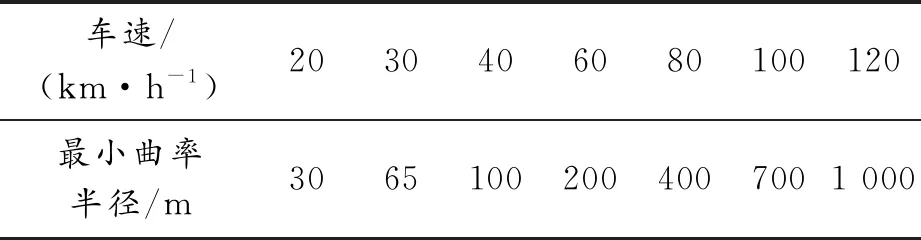
表4 弯道工况设计规范

依据表4可知，车辆行驶在实际道路上时，其转弯半径应大于等于该路段设计车速下对应的最小道路曲率半径。依据表3定义智能汽车路径跟踪车速取值范围为10～80 km/h。利用均匀性设计思想，以设计车速所规定的最小道路曲率半径为基准，划分如表5所示的88组不同的典型弯道工况。

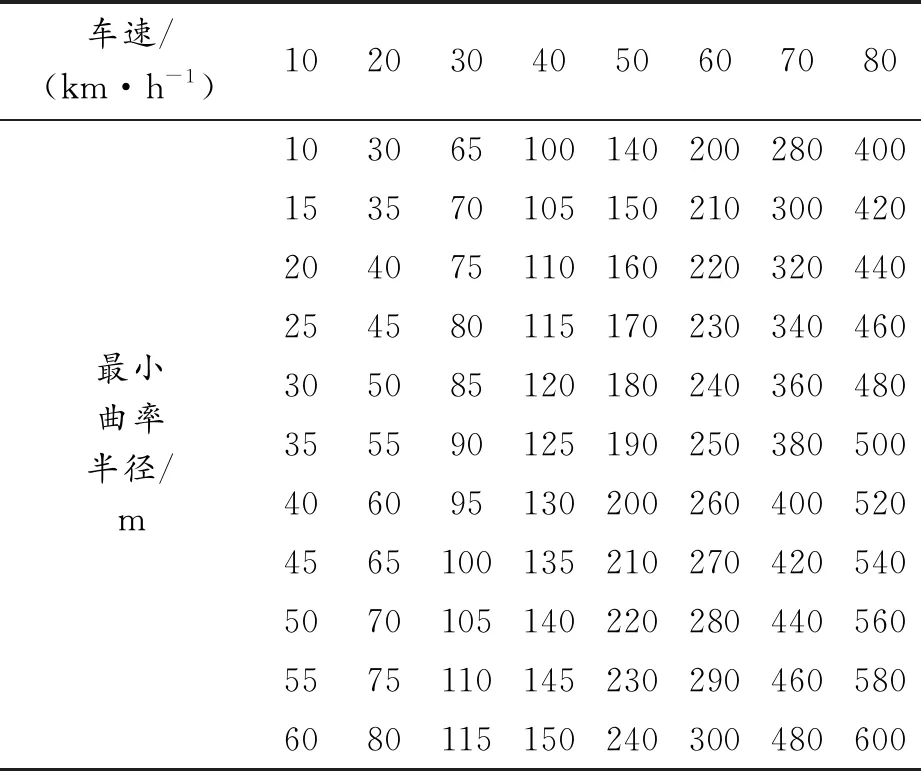
表5 典型弯道工况

4.2 基于遗传算法求解各工况下的最优时域参数

根据已有的研究可知，MPC控制器中的最优时域控制参数Np和Nc会受到纵向车速变化的影响[14]。如果取值过小，且速度较快时，车辆无法及时跟踪期望转角，最终导致路径跟踪控制失败；如果取值过大，则会增加系统的计算量，导致当前位置附近的跟踪误差增大，不利于路径跟踪控制器的实时性。因此，需要确定MPC控制器在不同弯道工况下的最优时域参数组合。但考虑到划分的典型弯道工况较多(88组)，用枚举法很难求出最优解。

遗传算法拥有强大的全局搜索能力、收敛速度快和搜索效率高等优点[15]，故选择利用Matlab中的Genetic Algorithm Toolbox工具箱调用遗传算法对时域参数进行优化。

确定优化目标为MPC控制器的时域参数矩阵K1=(NpNc)。为提升优化效率，预测时域取值范围Np∈(0，40]，控制时域取值范围Nc∈(0，20]。适应度函数为第3节所求得的不同仿真工况所对应的路径跟踪综合评价指标：

具体优化步骤如下：

1) 初始化时域参数矩阵，生成N个个体的种群；

2) 运行路径跟踪模型，计算相应个体的适应度函数；

3) 选取评分高的个体进行迭代优化，生成新的个体；

4) 为避免局部最优，随机选择少量进行变异操作。

设置遗传算法的初始种群数量为50，优化代数为20，交叉概率为0.5，变异概率为 0.1，算法优化流程如图4所示。

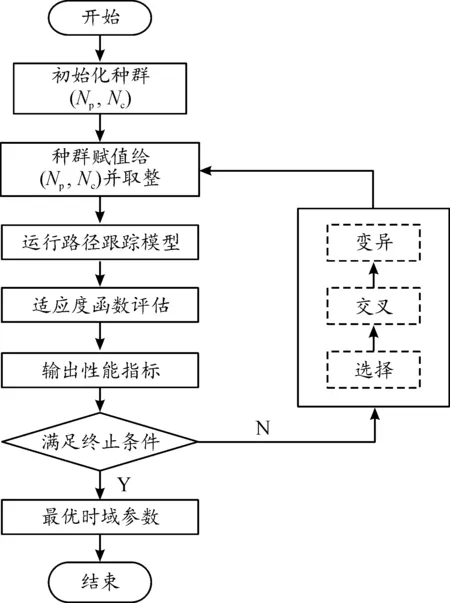
图4 遗传算法优化流程框图

将各组迭代优化后所对应的预测时域与控制时域作为对应工况下的最优时域参数组合，优化后结果如表6所示。

可以发现，在不同车速与道路曲率半径工况下，为使智能汽车具有最佳的路径跟踪精度及行驶稳定性，MPC控制器应选取不同的预测时域、控制时域。

4.3 建立时域参数自适应的MPC控制器

基于Simulink/Carsim联合仿真平台，在原有模型的基础上建立了时域参数自适应的MPC控制器。车辆在路径跟踪时，根据当前路面附着系数进行最优车速跟踪，系统实时输入当前车速和道路曲率半径，并根据表6将所求得的最优预测时域与控制时域组合(NpNc)输入模型预测控制器，以此得到时域参数自适应的智能汽车路径跟踪控制器，其系统整体结构如图5所示。

图5 自适应路径跟踪控制器系统整体结构

5 仿真试验

为了验证本文提出的考虑路面附着系数的自适应路径跟踪模型在对接路面工况的有效性，仿真试验设置了3种控制器对比控制效果，分别是：时域参数自适应MPC、仅加入最优车速约束的MPC和传统MPC。在Carsim中设定路面附着系数条件，仿真时通过设置Carsim中Target speed vs.station模块完成对期望速度的跟踪。图6为路面附着系数变化情况，路面附着系数在60 m处由0.8变为0.3。

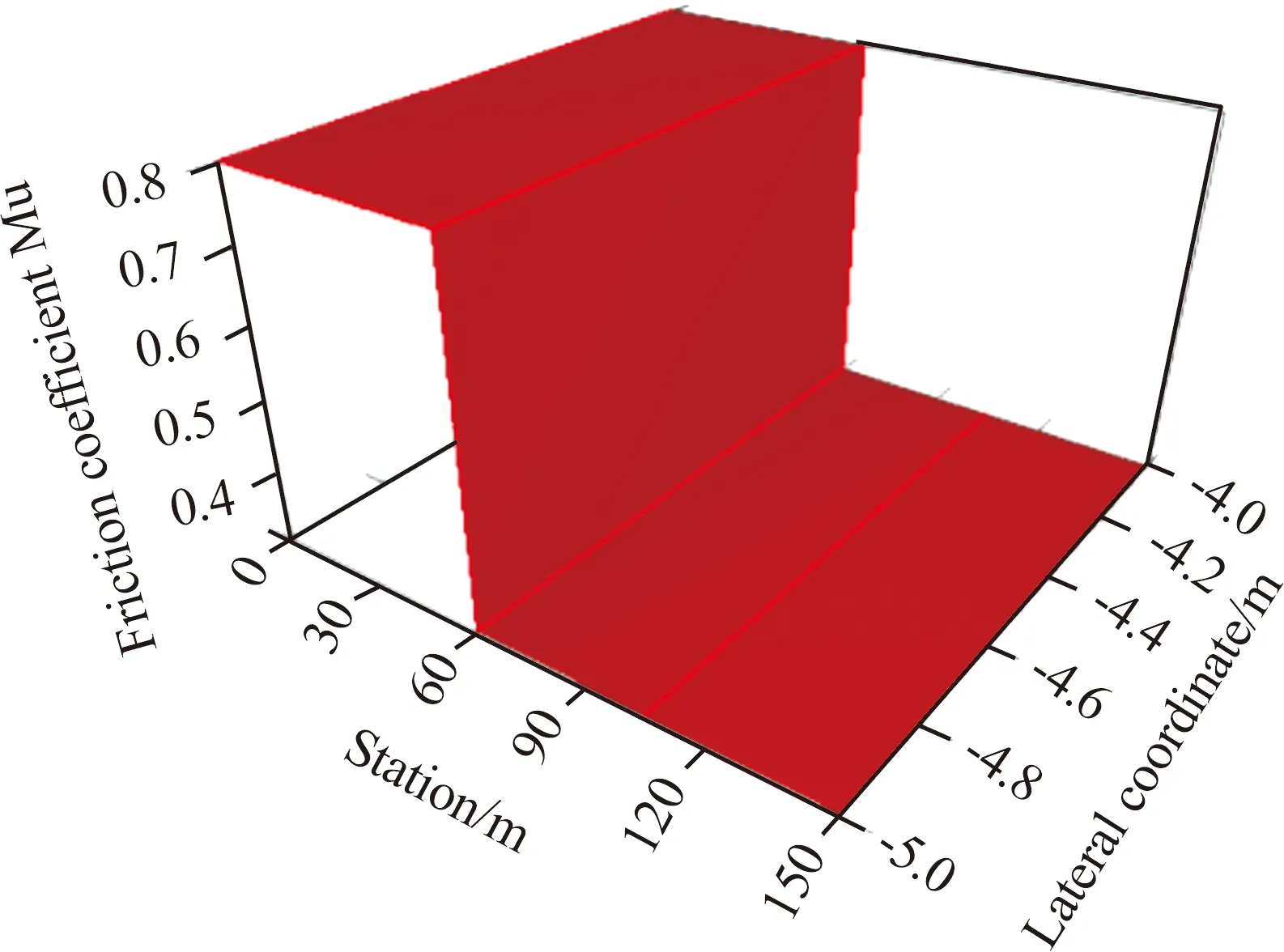
图6 路面附着条件变化

图7为路面附着系数由高到低的对接路面双移线仿真结果。图7(a)为车辆的期望最优车速与实际跟随车速变化，传统MPC的跟踪车速为定值60 km/h；图7(b)-图7(d)为车辆在不同控制器下的跟踪路径、侧向偏差、横摆角速度变化。由图7可知，在仿真开始时，3种控制器在高附着路面均有较好的控制效果。在车辆行驶至60 m后，路面附着条件发生变化，传统MPC控制器仍然以定速在低附着路面进行路径跟踪，侧向偏差与横摆角速度明显增大；加入最优车速约束的MPC控制器能应对路面附着系数突变的工况，但由于采用固定的时域控制参数，导致在低附着路面下跟踪误差较大；自适应MPC控制器根据工况变化采用合适的车速和时域控制参数进行路径跟踪，跟踪精度与稳定性最佳。

图7 对接路面仿真结果

为了验证该模型针对不同曲率工况的有效性，在Carsim中设置变曲率弯道工况并进行仿真试验。参考路径由一段蛇形、一段左转、一段移线工况拼接而成，路面附着系数为0.8，仿真车速均为60 km/h，对比时域参数自适应MPC控制器和传统MPC控制器跟踪效果。仿真结果如图8(a)-图8(d)所示。由图8可知，在单一路面附着系数的变曲率工况下，2种控制器均能完成路径跟踪，相比于传统MPC控制器，本文提出的时域参数自适应MPC在确保行驶稳定性的前提下，能有效提高跟踪精度。

图8 变曲率弯道仿真结果

不同控制器的路径跟踪仿真结果统计对比如表7所示。统计结果显示，本文所提出的自适应路径跟踪模型在对接路面双移线仿真试验中的最大侧向偏差为0.33 m，横摆角速度峰值为8.81(°)/s；在变曲率弯道仿真试验中的最大侧向偏差为 0.36 m，横摆角速度峰值为8.47(°)/s。相比于传统MPC路径跟踪模型，能够有效提高车辆在不同路面附着系数和道路曲率下路径跟踪的精确性和稳定性。