激励机制下保兑仓的道德风险研究——基于银行与第三方物流的博弈

黄鸿逸

(广东工业大学，广东 广州 510520)

1 引言

在供应链中,下游零售商多为中小型企业,信用较低,因此常处于资金紧张状态。这既不利于自身发展,又影响供应链整体的稳定性。为解决这一问题,保兑仓融资模式应运而生。该模式是依托于预付账款的融资手段,通过供应链中核心企业的帮助，使得下游中小企业因缺乏信用而导致融资难的问题得以解决。

保兑仓指的是以供应链金融中的生产商、经销商、三方物流企业以及银行等金融机构,联合签署的业务合作协议为基础运作的融资模式。在收缴保证金后，银行会为生产商放款，并为其开具承兑汇票。生产商在完成商品生产后将有关货物转交到第三方物流企业,物流企业负责仓储监管,并将仓单发给银行,经销商最后来物流企业仓库进行提货。保兑仓模式既缓解了供应链中部分中小企业的短期融资问题，还能有助于银行分散风险。

在整个供应链中,物流企业作为银行和融资企业间的桥梁,脱离于上下游关系,为融资企业保存货品，同时代替银行行使监管货物的权力。但第三方物流企业的监管费用由上下游偿付,银行与其只是存在较弱的契约关系,缺乏严格的监管责任。这一情况在徐绪松(2013)的研究中有所提及，其通过引入多局域世界复杂网络的思想深入推导了供应链中道德风险的演化规律。同时，彭路(2018)通过计量方法实证出农业供应链金融中道德风险的确存在放大效应。为了防范第三方物流企业的道德风险，早在20世纪90年代Yuk-Shee Chan(1990)等多位学者已提出通过在契约中添加激励机制能有效防控道德风险问题。为此，国内多项研究分别从完全信息与非完全信息、静态与动态、纯战略与混合战略等多角度探讨了引入监督激励机制后，供应链中的博弈结构模型的有效均衡点。基于均衡点的稳定条件所制定的供应链金融契约将对第三方物流企业形成有效约束，从而大大降低系统内的道德风险并且保证收益。

但是，过往的研究主要集中在针对核心企业与第三方物流企业的博弈讨论上。而事实上，银行正是为了寻求独立于供应链关系网络的第三方来行使自身监控权而与物流企业构成最紧密的联盟阵营。因此，如何在银行和物流企业之间形成有效契约，防止其中道德风险问题的产生以防范双方效益受到损害，这将是本文研究的重点。通过引入契约激励机制，本文采用演化博弈理论，通过构建银行企业与第三方物流企业在机制下的得益矩阵，探讨了双方风险分担以及有效均衡的稳定条件问题，并运用Matlab软件对结果进行仿真模拟，为银行与物流企业间的契约制定提供了建设性意见。

2 模型建立的基本假设和机制过程

2.1 基本假设

作为有限理性群体，银行企业和第三方物流企业都会以追求自身利益的最大化为目标。任何一方都会在博弈的过程中不断地调整自己的战略选择。

银行的策略分为抽查与无抽查，表示银行在单位时间内采取抽查策略的概率，第三方物流企业的策略分为审核与无审核，表示第三方物流企业对仓储情况采取审核策略的概率。同时，假设参数符号为：为供应链该项目订单；为项目中每件产品的平均生产成本；为项目需要支付给物流企业每件产品的库存监管费用；为物流企业存储每件产品所耗费的仓储费用；为生产商获得银行资金的贷款利率；为审核策略下物流企业需要花费的额外审核费用；为银行每次对物流企业进行抽查策略下的检查成本；为银行在抽查策略下，物流企业无审核情况所面临的罚金；Α为在实施奖罚激励机制下，物流企业被抽查到且自身有审核时，根据每件仓储货品可从银行处得到的额外补贴收益值。(=1,2,3,4)为银行在对应双方行动选择下所收到的风险损失期望。其中，<<<;>>。

2.2 模型构建

基于以上假设构建出银行与第三方物流博弈的得益矩阵，如表 1所示。

表1 博弈参与方的得益矩阵

2.3 演化均衡点及其稳定性分析

结合得益矩阵与Malthusian方程，银行的复制动态方程为：

()=dd=(1-)[(-+-+)+(-Α--++-)]

同理，第三方库存公司的复制动态方程为：

()=dd=(1-)[(Α+)-]

根据以上银行与第三方库存公司的复制动态方程，当()=dd=0,()=dd=0时，得出(0，0)、(0，1)、(1，0)、(1，1)、(，)为系统的5个不同均衡点，其中，

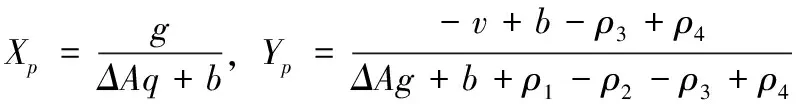
随后依次对、求偏导，可得雅克比矩阵()为：

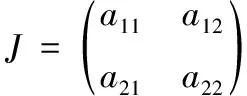
其中，

=(1-2)[(-+-+)+(Α--++-)]

=(1-)[(-Α--++-)]=(1-)(Α+)

=(1-2)[(Α+)-]

根据Friedman提出的雅克比矩阵(记为)的稳定性判定准则，当且仅当同时满足det>0和<0条件，均衡点才是演化稳定策略(ESS)。

通过求解，可得出系统局部均衡稳定时的主要参数取值,其中在点(，)处有+=0，不满足<0的条件，故该点肯定不是ESS而只是鞍点。因此，在已知且各参数均大于零的条件下，结合所有参数的不同取值来分析不同情况下4个均衡点的稳定性，如表2所示。

表2 均衡点的稳定条件及判别结果

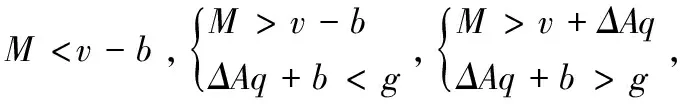
当满足条件<-，即银行抽查成本与抽中第三方物流企业没有审核所获得的罚金之差大于银行的抽查行为对未来风险损失期望的控制优化程度时，均衡点(0，0)为演化博弈的ESS，代表着“银行无抽查”“第三方库存无审核”的双方消极状态。假设参数集为：

=5000,=18,=35,=2,=008,=5000,=4000,=2000,Α=05,=48300,=50200,=52100,=54000

则(0，0)点稳定情况的相位变化如图1所示。

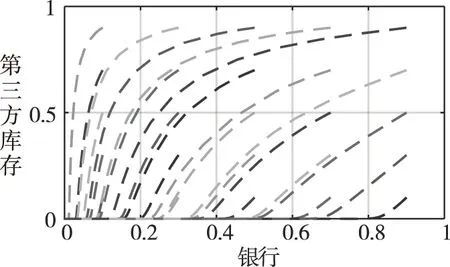
图1 (0，0)稳定情况的相位变化

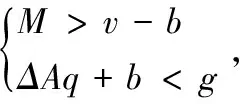
=5000,=18,=35,=2,=008,=5000,=4000,=2000,Α=05,=34800,=41200,=47600,=54000

则(1，0)点稳定情况的相位变化如图2所示。

图2 (1，0)稳定情况的相位变化

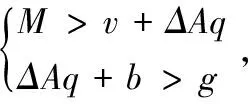
假设参数集为：

=5000,=18,=35,=2,=008,=5000,=4000,=3000,Α=05,=34503,=41002,=47501,=54000

则(1，1)点稳定情况的相位变化如图3所示。

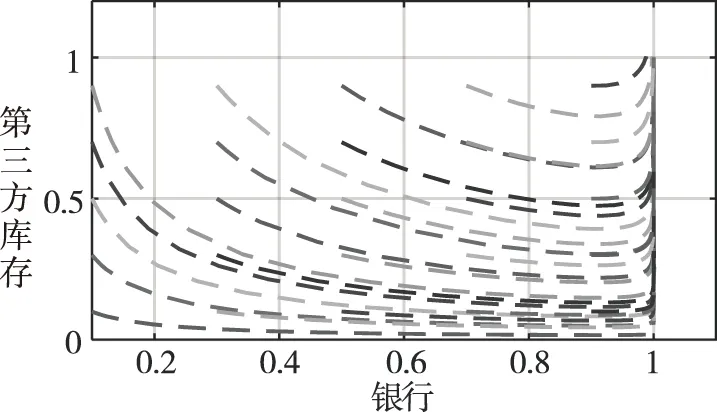
图3 (1，1)稳定情况的相位变化

3 激励机制下保兑仓的道德风险监管建议

通过上文的研究与分析，参考供应链金融中奖励机制的关键参数值。这可以使保兑仓中的银行与第三方物流企业的博弈，最终稳定在“银行抽查”“第三方库存审核”的双方主动的最理想状态。

其一，降低银行抽查成本。银行的抽查成本是银行是否愿意采取抽查策略的最关键所在。若能有效降低银行抽查，尤其是单次抽查成本，将极大提高银行在保兑仓的双方博弈中的积极性。就目前供应链金融的发展来看，最适合的方法莫过于利用区块链技术。区块链技术由于自身所具有的可追溯和不可篡改性，能够提高供应链金融的透明程度，在防止单点数据被轻易篡改的同时，信息得到同步更新，降低了抽查成本。其二，奖励机制中奖、罚的适当性。从博弈稳定条件可发现，若想稳定在最理想的“银行抽查”“第三方库存审核”双方主动状态，补贴总收益不宜太高，这会增加银行负担；罚款金额不宜太低，不然难以对第三方物流企业形成约束。而两者的关键平衡点即为稳定条件中的不等式，该不等式很好地为将来需要通过奖励机制来管控保兑仓中道德风险的相关条款设置提供了良好的参考意义。