融入信息技术的HPM教学研究

周佳豪，代可可，薛鉴伟

（江苏大学，江苏镇江 212013）

近年来，信息技术与不同学科的结合逐渐获得各科教师的认可，而数学史视角下的课堂教学也日益受到广大教育工作者们的关注。在现代数学教学中，信息技术与数学史的融合的趋势必不可挡。例如，中学教师在讲解球的体积时，若想将刘徽的“牟合方盖”和“祖暅原理”很好地融入其中，仅靠口头讲解和板书是无法做到的，这时若教师通过信息技术，例如，GeoGebra动态地展示牟合方盖的构成和祖暅的“缘幂势既同，则积不容异”的定理，既有助于学生的理解，又培养了学生空间观念与几何直观能力。可以说信息技术是数学史与数学教育联结的一条纽带。

一、传统HPM教学的优点与不足

法国数学家庞加莱曾说过预测数学未来的适当途径就是研究数学的历史，这句话是我们为什么要学习数学史的一个有力解释。同时，数学史揭示了数学的概念，定理的产生和逐步发展的过程，以及在发展过程中对数学思维和方法的运用。HPM视角下的数学教学，就如同弗赖登塔尔的“再创造”理论所描述的那样，是在有意识地调节教材中知识结构与顺序，模仿历史上知识产生和发展的过程进行教学。这样在一定程度上回答了学生问：“为什么要学习这个知识，怎样想到要这样处理这个问题？”这一类的问题。此外，通过数学史的学习，学生得以感受到并且理解数学的美。数学的美体现在它的普适性，和谐性，例如，《几何原本》中所提及的黄金分割，被认为是最能引起美感的比例，这一发现不仅在数学上有着广泛应用，也在建筑和艺术方面有所显现，在帕特农神庙和《蒙娜丽莎》中都能找到它的影子。斐波那契数列，对数螺线也极具美感，在课堂上普及这些内容增长的不仅仅是学生的知识，还有学生学习数学的兴趣。

HPM视角下的教学有明显的优点，这使得广大一线教师在教学中有意地融入数学史知识，但是在融入的过程中又出现了一系列问题。比如融入方式的刻板性，汪晓勤教授曾提出了四种将数学史融入数学教学的方式，分别为：附加式、复制式、重构式以及顺应式。目前，大部分教师都局限在这几种融入方式中，对于融入方式没有独到的创新。当代教师对信息技术的不灵活，也是数学史在数学课堂的整合更加僵化的重要因素。大多数老师仅仅通过讲数学家的鼓舞人心的故事，将数学史整合到课堂教学中，或通过PPT展示数学家的图片，这样很难将数学史中特别是几何发展史中所蕴含的数学思想方法传授给学生。这使得一些应当融入数学课堂的数学史知识却难以融入数学课堂。

二、信息技术环境下的HPM教学

融入于信息技术的HPM教学就是在教学中以信息技术为媒介，将数学史中蕴含的，难以口头表述的知识的内涵和本质以动态的，可视化的方式展现出来。数学史内容如烟波般浩渺，而数学知识极具逻辑性与抽象性，信息技术此时如同两者之间的纽带，在感性的数学历史文化和理性的数学逻辑体系之间建立联系，使数学史中抽象的理念变成可见的图形。这打破了传统数学史教学中某些繁杂知识特别是几何中“只可意会，不可言传”的阻碍。

信息技术环境下的HPM教学并非只是简单的PPT制作，“HPM”微课，它真正的优势凸显在课堂上使知识的传授具有可操作性、灵活性和主动性。

以GeoGebra为例，GeoGebra可动态地展示数学史中那些晦涩难懂的，难以用语言表述的内容。HPM教学中讲解圆的体积必会提及牟合方盖，若通过口头讲解“取立方棋八枚，皆令立方一寸……”必会让学生觉得教师不知所云，但教师又难以绘图，唯一能做的只是找几张图片而已。但GeoGebra中，通过指令输入等一步步操作，可以动态地展示牟合方盖的构造过程，让学生知其然知其所以然。信息技术使HPM教学更加倾向于数学实验课，让学生在信息技术所创设的问题情景中感知数学，在概念的形成中理解数学。

预设和生成是新课程所倡导的一个重要的教育理念，一些教师难以把握预设和生成的关系，使得HPM教学要么完全以教师为主导，一个人自顾自地讲准备好的故事，死气沉沉，要么让学生激起兴趣却脱离教师控制，无法收场。若教师以GeoGebra为载体，利用软件独特的优越性，可即时地更改问题数据，使图形产生动态变化，让学生在图形运动变化过程中寻找不变量或比例关系，发现图形隐藏的数学原理。或者更改条件，对数学史中的方法进行适当调整，让学生在巨人的肩膀上继续探究，获取新知，增长才干。信息技术环境下的HPM教学以一种极具灵活性的方式，激发学生兴趣，让学生在教师的引导下自主探究，可以算作启发式教学的一个有效途径。

社会经济快速发展，一些发达地区基本可以实现在课堂上人手一机。在HPM教学中，若学生人手一机，让学生对教学内容和相关史料进行自由探索，利用计算机软件进行绘图以开拓思路，发现结论，必将对学生的自主学习能力，动手能力，细心品质的培养具有很大益处。此时，学生真正地成为了课堂的主人，而教师则是充当一个引导者，监督者的角色。这样的方式与布鲁姆的发现学习理论不谋而合。

三、数学史内容的可视化呈现——以利用祖暅原理求球体体积为例

《九章算术》的“少广”章中记录了一个已知球的体积求直径的问题，文中给出的方法为“开立圆术”，得出球的体积与直径的关系。我国魏晋时期数学家刘徽在为《九章算术》作注时对这个关系提出疑问，他创造了一个称之为“牟合方盖”的立体几何图形，他希望借助“牟合方盖”得出球的体积，但他失败了。直到两百多年后，祖氏父子利用“牟合方盖”得出了球体的体积公式。祖暅之《缀术》有云：“缘幂势既同，则积不容异”。意思是说：介于两个平行平面之间的两个立体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个立体的体积相等。这就是“祖暅原理”。而在西方，这个定理由意大利的数学家卡瓦列里提在1635年出版的《连续不可分几何》中才提出，祖暅发现定理的时间要比他早1100多年。

这是中国数学史中典型的空间几何体问题，在各式各样的教学软件中，GeoGebra具有其他软件难以比拟的3D绘图功能。它的3D绘图区的优势在立体几何教学过程中的应用最为显著，它可以完美地显示三维空间中空间几何的特定特征，同时代数区域和3D绘图区域可以同步更改，这对中学生数形结合思想的培养具有很好的促进作用。下面，我们来说明利用GeoGebra进行利用祖暅求球体积教学材料的设计。

第一部分，探究祖 原理。第一步，在空间内构造两个平行平面，并在下平面上构造多个面积相等的多边形。第二步，利用GeoGebra的棱锥工具，以第一步构造的多边形为底面，在另一个平面取点为顶点，构造平面间高度相等但棱长不等的棱锥。第三步，在两个平面之间再构造一个可滑动的平行平面，并且制作一个滑动杆以控制这个平面上下平移，构造滑动平面与两个平面的截面。第四步，利用工具栏中面积，体积的度量工具度量棱锥的体积与截面的面积，探究其比例关系和大小关系。第五步，通过改变棱锥顶点位置改变棱锥倾角和改变两平面距离改变棱锥高度，从棱锥体积与面积的变化中寻找不变量，总结出“缘幂势既同，则积不容异”的规律。

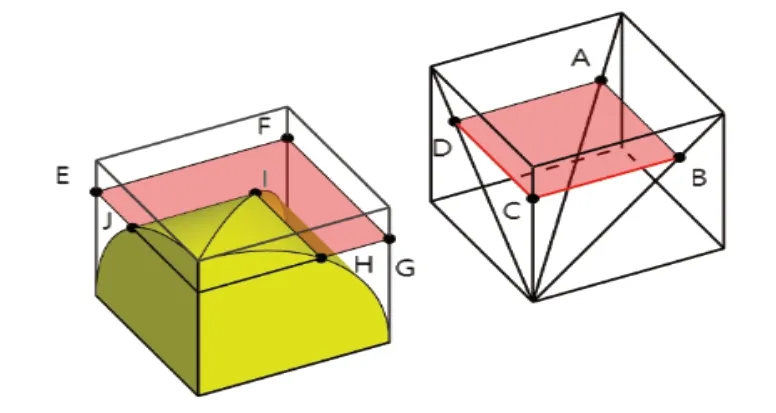
第二部分，构造牟合方盖。第一步，“取立方棋八枚，皆令立方一寸，积之为立方二寸“，就是构造一个由八个棱长为r的小正方体组成的大正方体，这里可以先作一个大正方体，再作虚线将大正方体分成八份可以产生同样的效果。第二步，“规之为圆囷，径二寸，高二寸。又复横规之”，就是在水平方向作一个正方体的内切圆柱，再在竖直方向做一个正方体的内切圆柱。“则其形有似牟合方盖矣”，这时两圆柱相交，只保留圆柱相交的部分，将正方体和圆柱的其他部分隐去，得到的就是牟合方盖。

第三部分，构造八分之一个牟合方盖和“外棋”。第一步，作三个相互垂直的平面，将牟合方盖平分为八份，取其中之一，将其余部分隐去。若第二部分构造正方体时，以原点为中心，这里可以设置只显示某一个象限即可。第二步，“外棋”的形状比较复杂，祖氏父子便利用“缘幂势既同，则积不容异”的原理构造了一个方锥，在等高处方锥的横截面积和三个“外棋”的横截面积之和相等，方锥的高与“外棋”的高相等，这样方锥的体积便和“外棋”的体积相等。这里构造一个底面与八分之一个牟合方盖底面面积相等且在同一平面内的正方体，在正方体中以正方体的上底面为底，下底面的一个顶点为顶点，构造出方锥，方锥的体积即为正方体体积的三分之一。

四、具体实施过程

将信息技术与HPM教学相结合形成了一个相对复杂的教学结构，各个结构之间的关系决定了如何将信息技术、数学史和数学教学整合在一起的方式。在信息技术环境下的HPM教学中，数学史是数学知识，数学理念的载体，而信息技术仅是展示的一种媒介。因此在具体实施过程中，应以数学史的融入为主，而不是过分执着于信息技术的表现方式，要避免华而不实。笔者将实施过程分为了三部分。首先，课程内容与数学史的整合，课程中涉及的数学史知识要么以《几何原本》等古代著作为蓝本，要么是典型的定理、命题，如尺规作图，赵爽弦图；或者以生活实例为载体，如泰勒斯测金字塔等，将其整合到课程中的重点就是抓住数学史与数学知识的内在联系。其次，通过信息技术，将课程中的数学史以可视化、多元化的方式呈现，让教学资源更加直观化、高效化。最后，利用制作的资源进行教学设计，合理设置各个环节。在教学中，利用信息技术自然地将数学史中蕴含的精髓展示给学生，充分发挥数学史的育人作用。

五、不足与建议

在HPM教学中使用信息技术尽管对于传统的HPM教学优势十足，但在具体实施过程中仍有许多问题。第一，教师本身对数学史知识的缺乏，或者缺乏应用意识，这是难以具体实施的一个关键因素。第二，就是一线教师的信息技术水平有限，且缺乏时间或精力学习可视化软件的使用，教师缺乏终身学习的意识。第三，信息技术的使用使数学史以可视化的方式呈现，但这更适用于几何部分的内容，对于代数部分的内容还是难以展现。

在这里，笔者提出几点合理建议。第一，教师要在教学中融入数学史和使用现代信息技术的主观意愿，学校可组织教师进行这方面的培训，使教师之间可以相互交流、切磋和促进。第二，理论要联系实践，信息技术支持的HPM教学不能只处于研究理论中，要真正运用于教学中，这样才能不断发现问题，第三，可以建立完善的可视化的数学史资源库，形成资源共享，这样可以节省教师的时间与精力，让教师易于和乐于使用信息技术将数学史融入教学中。