近亲结点图编辑的Self-Training算法

刘学文，王继奎，杨正国，易纪海，李 冰，聂飞平

1.兰州财经大学 信息工程学院，兰州 730020

2.西北工业大学 计算机学院，光学影像分析与学习中心，西安 710072

传统有监督分类利用有标签的数据训练分类器，但是有标签样本的获取通常困难、昂贵或耗时。为了克服有监督分类的缺点，建立更具泛化能力和高性能的分类器[1]，研究者提出了半监督分类。半监督分类属于半监督学习（semi-supervised learning，SSL）[2]的范畴，半监督学习利用大量无标签数据和少量有标签数据，旨在解决人工成本高昂和分类准确性等问题。从20世纪末到21世纪初，半监督学习领域陆续出现了许多方法，例如自训练（self-training）[3-8]、直推学习（transductive learning）[9-10]、生成式模型（generative model）、协同训练（co-training）[11-13]等。

Self-Training算法基于自身迭代学习，不断地将高置信度样本及其预测标签加入训练集，如果样本被误分类而加进了训练集，此错误将会在迭代过程中不断加深，因此Self-Training算法的效果很大程度上取决于高置信度样本的识别准确度。文献[14]提出SETRED算法，通过在相关邻近图（RNG）上统计样本点割边权重（cut edge weight），利用CEW[15]方法选择高置信度点，其分类性能好，但是该算法构造RNG的复杂度较高。半监督分类需要满足一些基本假设，常用的基本假设有平滑假设（smoothness assumption）、聚类假设（cluster assumption）和流形假设（manifold assumption）[16]。文献[4，17]基于聚类假设利用FCM算法的类别隶属度阈值筛选高置信度样本点，但是当样本类别数较多时阈值的设定较为困难。当前已有研究者将流形学习与半监督学习结合起来，通常这类半监督方法不仅复杂且参数调节较为繁琐[18]，对噪声较为敏感。聚类假设主要考虑数据的整体特性，而流形假设主要考虑数据的局部特性。为兼顾整体与局部特性。文献[19]提出STDP算法，利用密度峰值[20]潜在的空间结构，先将有标签样本的前驱作为高置信度点，再将有标签样本的后继作为高置信度点。文献[5]通过设定局部密度阈值，依次将有标签样本中的核心点、边界点作为高置信度点添加进训练集。上述两个方法的迭代速度非常快，但是没有数据编辑步骤以去除误分的高置信度样本。文献[21]在文献[19]的基础上结合CEW方法提出STDPCEW算法，利用数据编辑技术对选取的高置信度样本进一步优化，但是STDPCEW和SETRED均需要构造RNG，造成算法的整体复杂度高，难以适用于大规模数据集。

在密度峰值聚类思想的启发下，提出了一种近亲结点图编辑的Self-Training算法（self-training algorithm with editing direct relative node graph-DRNG）。DRNG算法主要工作如下：

（1）利用密度峰值定义样本间的原型关系，并构造出近亲结点图这一新型数据结构。

（2）采用假设检验的方式识别近亲结点图中的高置信度样本。综合考虑密度与距离两个方面定义了近亲结点之间割边的非对称权重，减小了高密度样本点被误分类的概率。

（3）采用最近邻（nearest neighbor，NN）分类器作为基分类器，提出了近亲结点图编辑的Self-Training算法（DRNG），在8个基准数据集上进行实验，实验结果验证了DRNG算法的有效性。

1 相关工作

1.1 符号

将文中出现的部分符号及其说明列在表1中。

表1 符号及其说明Table 1 Notations and illustrations

1.2 DPC

密度峰值聚类[20]（DPC）是2014年由Rodriguez等人在Science期刊上提出的一种聚类算法，Rodriguez等人给出了两种计算局部密度的方式，分别为截断核（cutoff kernel，见公式（1））和高斯核（Gaussian kernel，见公式（2）），样本xi的局部密度定义为：

样本xi的峰值定义为：

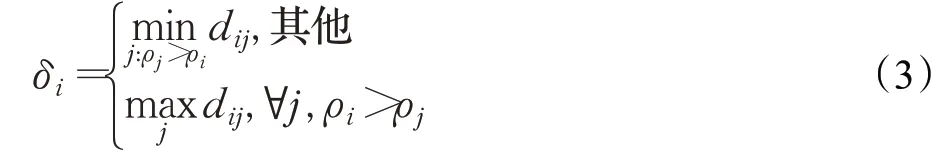
DPC的机制在于选择具有较大局部密度和峰值的样本点作为潜在的类簇中心，在选取类簇中心之后，将剩余非中心点递归分配给距离其最近且密度大于它的样本点完成类簇划分。

图1所示为3类别Iris数据集的二维投影和对应的密度峰值分布决策图。图1中子图（a）和（b）中数字表示样本点密度与峰值之积即γ=ρ×δ的大小顺序，图中标记了前5个样本点。点1的密度和峰值最大被选为类簇1的中心，点2的密度虽然接近于点3～5，但是其峰值明显大于后者，其被选为类簇2的中心，同理点3被选为类簇3的中心。

DPC的特性在于无需先验知识选取类簇中心，利用峰值所隐含的层级关系，低密度点会跟随高密度点，类簇划分只需一步，速度极快。通过密度和峰值的层级关系将空间内的样本点联系在一起，不受类簇的形状约束，能够在任意形状分布上进行聚类。因为异常点数据的局部密度较小，对类簇中心选取影响较小，难以影响类簇划分，所以DPC对异常点也不敏感。

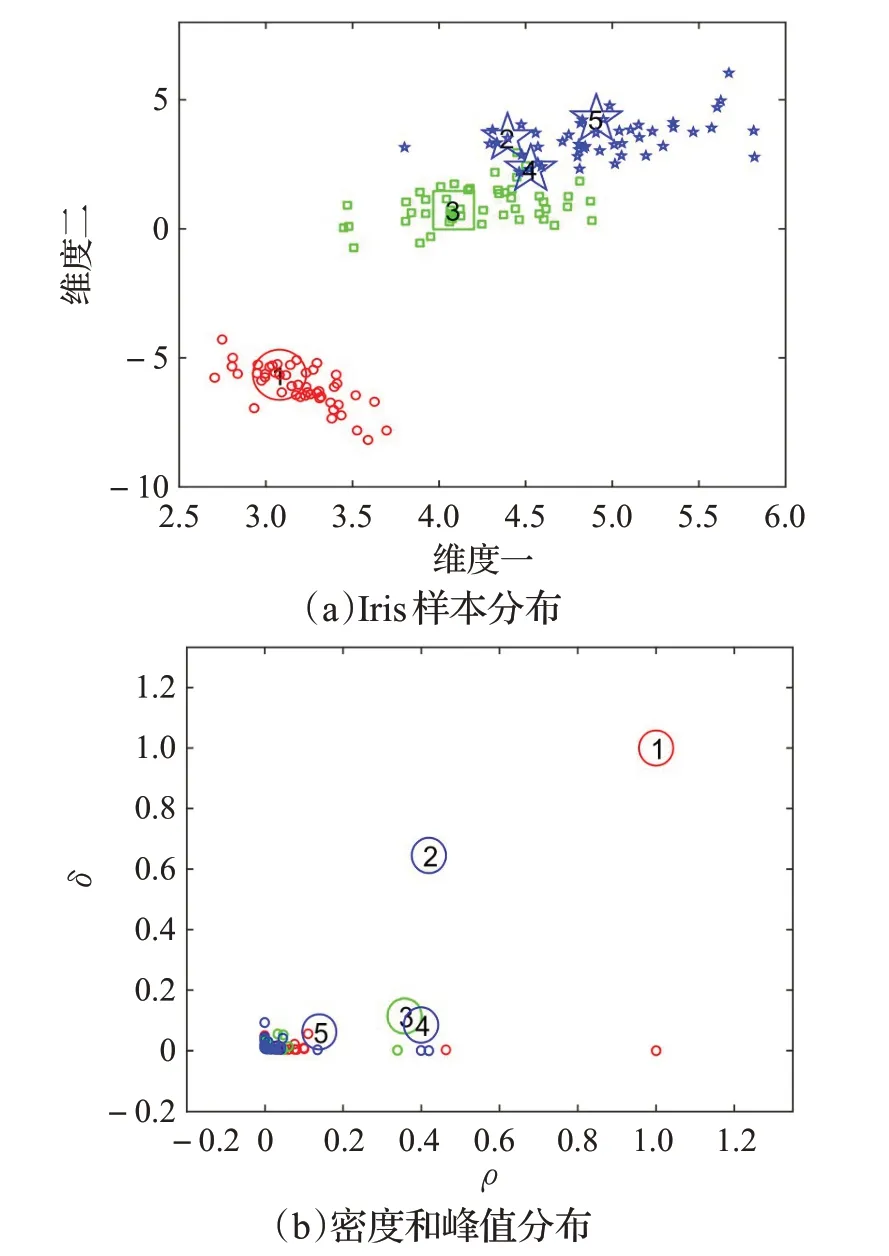
图1 Iris样本分布和密度峰值分布决策图Fig.1 Samples distribution of Iris and density peak distribution with decision diagram

DPC也存在一些不可忽视的问题。密度和峰值的计算复杂度为O(n2)，计算复杂度高。密度和峰值依赖于距离计算，在高维数据上这种相似性度量方式将失效，使得DPC难以发现数据真实结构。截断距离的取值没有考虑到样本局部特性，对于密度不平衡的样本表现欠佳。近年来，有关DPC的研究热度不减，不少研究者对DPC的缺陷进行了改进，例如文献[22-23]分别从相似性度量和聚类簇中心选择方面对DPC进行了优化。

1.3 Self-Training相关算法

Self-Training是一种开放性的包裹算法，是非常灵活的学习框架，可以嵌入不同的基分类器，也可以采用不同的高置信度样本选取方案，能适应内容多样的半监督学习任务。Self-Training的半监督分类性能取决于高置信度样本的选取质量和基分类器的性能。Self-Training算法的复杂度主要由基分类器的训练和预测以及高置信度样本的选取这几个过程所决定。

Self-Training不同于生成模型需要估计参数，当有标签样本稀缺时会得到错误的模型；也不同于协同训练一样基于特定的、实际情况下不容易满足的假设条件。接下来介绍4个相关的Self-Training算法。

1.3.1 SETRED

SETRED[14]首先从L中训练分类器H，再从U中抽取部分样本U′，根据最近邻规则（NN Rule），从U′中选取由H标记后的置信度较高的样本S′，将L⋃S′作为潜在训练集并构造相关邻近图（RNG）。RNG内拥有不同样本标记的两个顶点所构成的边为割边（cut edge），RNG内与样本点xi有边相连的所有样本点的集合Ni为其近邻集。若某一样本点与其近邻之间存在大量的割边，则将其视为存疑样本点。

SETRED利用CEW[15]方法识别S′内可能误标记的样本，在去除误标记的样本后，将更高置信度的样本S″加入到训练集中。SETRED有效提升了半监督分类性能，但其构造RNG的过程耗时较长，在规模较大的数据集中受限。

1.3.2 STSFCM

STSFCM[17]通过在Self-Training过程中集成聚类方法，通过聚类发现无标签样本中的潜在空间结构，训练更优的分类器。

STSFCM将SSFCM[24-25]和SVM组合，在每次迭代过程中先由SSFCM计算无标签样本点xj∈U的隶属模糊系数bij,i∈[1,c],c为样本类簇数量，ε1为置信度阈值，从中选取b≥ε1的样本点构成无标签样本集U′；然后在L上由SVM训练分类器H，由H输出样本点xk∈U′的隶属度fik,ε2为置信度阈值，从U′中取f≥ε2的样本点构成高置信度样本集合S′。若S′=∅则在下一迭代过程中减小ε1的值。

1.3.3 STDP

STDP[19]将DPC[20]算法集成到Self-Training过程中，利用DPC发现样本空间潜在的类簇结构，改善分类器性能。STDP首先在L上训练分类器H，选取L内样本点的无标签前驱样本构成集合U′，U′⊂U，由H赋予其标签构成高置信度样本集S′，更新L←L+S′，U←U-S′，重新训练H；然后再选取L内所有样本点的无标签后继构成集合U″，U″⊂U，由H赋予其标签构成高置信度样本集S″，更新L←L+S″，U←U-S″。

STDP迭代速度非常快，但STDP未进行数据编辑去除S′和S″内的误分类点，其性能还有提升空间。

1.3.4 STDPCEW

STDPCEW[21]融合了SETRED[14]与STDP[19]算法。依次选取L内所有样本点的无标签前驱和后继样本作为高置信度样本S′，在L⋃S′上构造RNG，再利用CEW[15]方法识别并去除S′内误标记点，更新训练集并返回重新训练后的分类器。STDPCEW相比SETRED定义了不同的割边权重，其新定义如下：

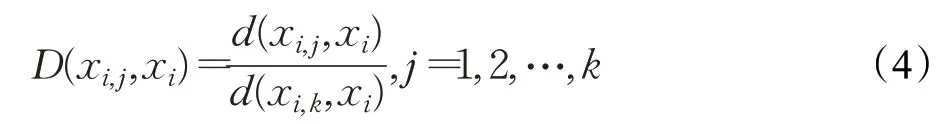
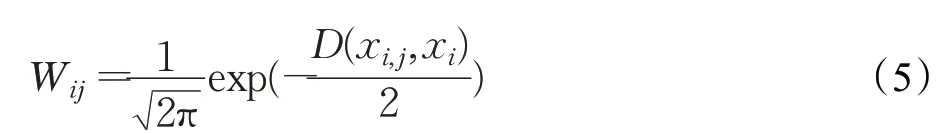
其中，d(xi,j,xi)表示样本点xi与在RNG上的第j个近邻的距离，D(xi,j,xi)表示样本点xi与在RNG上的第j个近邻的归一化距离。

STDPCEW相比STDP新增了数据编辑步骤，但其构造RNG的过程却使其复杂度提升到O(n3)。STDPCEW牺牲计算时间换取了分类性能的提升。

2 近亲结点图编辑的Self-Training算法

为降低Self-Training算法迭代过程中的高置信度样本被误分类的风险，提升半监督分类性能，本文提出近亲结点图编辑的Self-Training（DRNG）算法。

DRNG利用DPC[20]获取样本集X内空间结构潜在的原型关系。

定义1样本xi的原型Pi为：

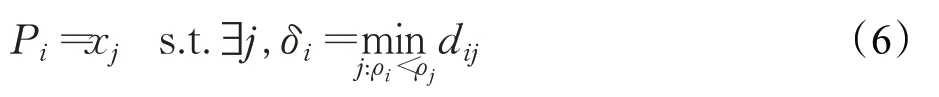
其中，dij=‖xi-xj‖2,ρi和δi分别表示样本xi的局部密度和峰值。

从定义1可以看出，原型关系是非对称的偏序关系，是一种特殊的带有方向的近邻关系。由DPC的机制和特性可知，峰值融合了距离和密度信息，隐含了低密度点跟随高密度点的指示关系，DRNG将这种关系抽象的表示为原型关系。

2.1 构造原型树

DRNG利用原型关系构造原型树，先由公式和计算各样本点的局部密度ρ和峰值δ，再构造出原型树，步骤如下：

（1）确定根结点：局部密度最大的样本点作为根结点，即根结点xr须满足∀j,ρr≥ρj。

（2）确定父结点：结点xi的原型Pi为其父结点，即xi的父结点满足xj=Pi。

图2所示为由包含3个类别的高斯分布数据所构造的原型树，其中星形、矩形和圆表示不同类别样本点，为便于展示只选取了处于中心位置的一些结点。

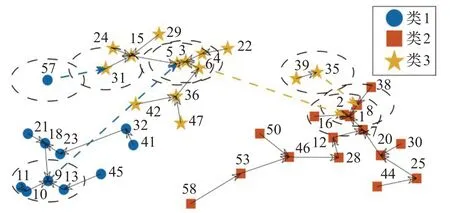
图2 原型树部分结点Fig.2 Part of prototype tree node

如图2所示，数字表示局部密度的大小顺序，1表示该样本点的局部密度最大。箭头所指向为某一样本点的原型，如样本10的原型为9。按照密度由大到小的顺序遍历样本，确定根结点和其余样本的父结点，构造出原型树。实线箭头指向相同类别的原型，虚线箭头指向不同类别的原型。为了利用样本间的原型关系来选取高置信度样本点，定义近亲结点集和近亲结点图。

定义2样本xi的近亲结点集Fi为：

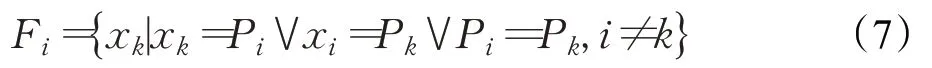
由定义2可知，样本xi的近亲结点集由样本xi在原型树上的父亲、兄弟和儿子结点构成。近亲结点集Fi中的元素称为样本xi的近亲。

如图2所示，样本点3的近亲集合Fi={x2,x4,x5,x6,x16},其中样本点2是样本点3的父结点，样本点4、5、6是样本点3的子结点，而样本点16为样本点3的兄弟结点。。

定义3样本xi的近亲结点图Di为：

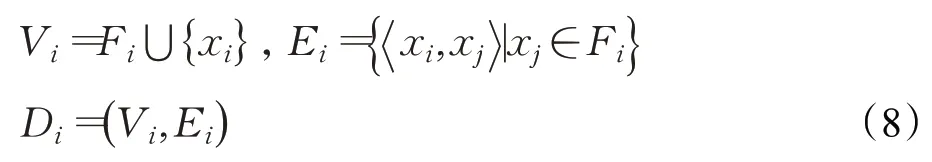
其中，Vi表示Di的顶点集，Ei表示Di的有向边集。

由图2原型树构造图3样本点3的近亲结点图D3。如图3所示，D3中顶点2、4、5、6和16与顶点3存在有向边连接，顶点3的出度为5，且E3={x3,x2,x3,x4,x3,x5,x3,x6,x3,x16}。

图3的子图（a）是包含样本点3与近亲之间的近亲图，子图（b）是仅包含有割边的近亲图。DRNGE利用近亲结点图来确定高置信度样本，将识别出的高置信度样本和其预测标签添加到训练集。

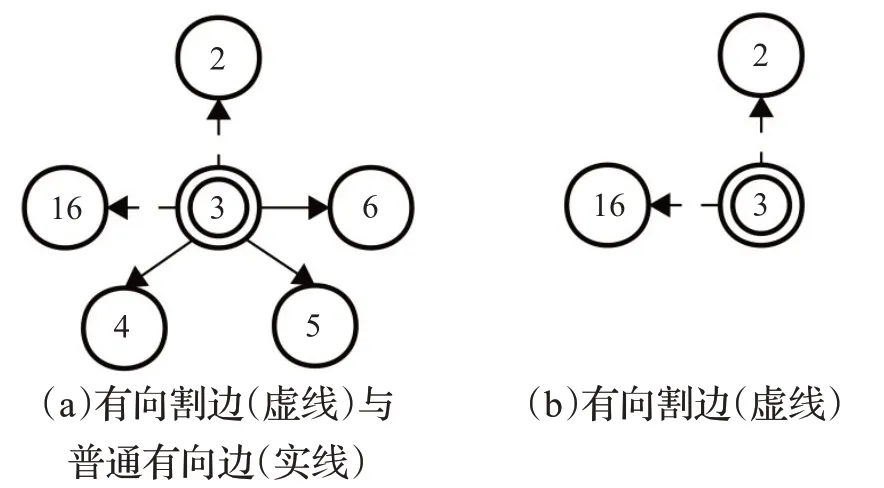
图3 样本点3的近亲结点图和割边Fig.3 Direct relative node graph of sample point 3

2.2 近亲结点图编辑

与CEW[15]方法一样，DRNG中一条连接具有不同标签的两个顶点的边为割边（cut edge），若某个点与大量割边相联系，显然它的周围存在大量不同类别的样本，其被误分类的概率较大，因此可以对样本点的割边权重进行统计以识别高置信度样本。DRNG通过统计近亲结点图中的割边权重来识别高置信度样本。

定义4样本xi与近亲xj之间的割边权重qij为：

显然割边权重是非对称的，即通常情况下qij≠qji，样本的密度越大，其割边权重也越大。

定义5样本xi的割边权重和Ji为：

如果样本xi和xj属于同一类别，则Iij=0；否则，Iij=1。DRNG与CEW[15]方法类似，也利用假设检验的方式识别高置信度样本。

定义6零假设H0：样本标记过程互相独立且服从同一概率分布，为有标签样本中第k类样本集，πk为初始有标签样本L内的第k类样本的先验概率，c为类簇个数。

假设Ji近似服从正态分布，由公式可以计算其在H0下的均值和方差：

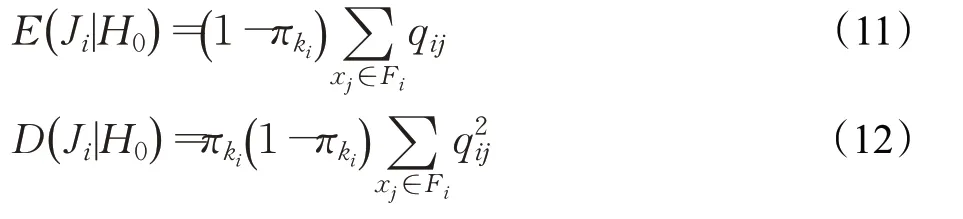
其中，πki为样本xi属于类别k的先验概率。

显然高置信度样本会有更小比例的不同标签的近亲结点。因此为更高效地识别高置信度的样本，采用假设检验的方式，设定一个显著性水平θ，凡是落入左拒绝域内的样本将作为高置信度样本加入到训练集中，而落入左拒绝域右侧的样本将被丢弃。

在图2原型树中，虚线连接不同类别的点，如点8为类2内的点，点35为类3内的点，这两个点构成的边即为割边。通常情况下，Self-Training迭代过程中密度越大的样本误分后对分类性能的影响越大。从图2可以看出，点8的密度显然大于点35，而点8距离点1和点2非常近，一旦点8被误分类，很可能将错误蔓延至点1、2、7、16和38，从而导致误分类风险增大。

近亲结点图具有以下三点特性：

（1）存在边连接的两个近亲结点是原型树上的“近邻”，可能相距较远而非一般距离空间上的近邻，比如图2中点5和点9，这两个点都位于不同的局部密度中心区域。

（2）利用原型树结构中低密度跟随高密度点这样一种特性，即使是在非球形分布数据上，所获取的高置信度样本质量仍然比较高。

（3）近亲结点图中各结点构成的边为有向边，两个结点之间的边权重是非对称的，密度越大权重越大。非对称权重增大了密度大的样本点的割边权重和，使其落在左拒绝域内的概率降低，从而减小大密度点误分导致跟随的小密度近亲点也被误分的风险。

DRNG与类似Self-Training算法都存在误分的可能性。STSFCM[17]通过隶属度阈值过滤掉置信度低的点，但可能由于FCM对于非球形数据的聚类效果不理想、初始点选取不当等原因，导致有标签样本邻近的无标签样本被误分；SETRED[14]、STDPCEW[21]和DRNG都采用了CEW方法，当数据较少且数据分布不太符合假设的正态分布时，假设检验的效果可能不理想；STDP[19]、STDPCEW和DRNG都利用了密度峰值发现潜在空间结构，当数据密度不平衡、高维数据距离失效或者截断距离dc设置不合适时，发现的空间结构可能与实际结构偏差过大，导致误分错误风险累积、高置信度样本质量降低。

2.3 DRNG算法

DRNG算法利用假设检验识别出近亲结点图中的高置信度样本，并将高置信度样本及其预测标签添加至训练集，迭代训练分类器。DRNG算法步骤在算法1中列出。

算法1DRNG算法

输入：有标签样本L，无标签样本U，已有标签YL，截断距离比例阈值α，显著性水平θ

输出：分类器H

参数：左拒绝域阈值τ

1.根据公式（2）和（3）计算局部密度ρi和峰值δi

2.根据定义（1）计算样本的原型Pi并构造原型树T

4.在有标签样本集L和YL上训练分类器H

6.在原型树T中搜索L中样本的无标签近亲结点集L′，利用分类器H赋予L′中样本标签

7.利用T，在L⋃L′中构造近亲结点图，计算割边权重qij和随机变量Iij

9.根据公式和计算E(Ji|H0)和D(Ji|H0)，得到Ji的分布，计算左拒绝域阈值τ

10.若Ji的值落在左拒绝域阈值τ右侧，则将xi从高置信度样本中移除，L″=L′-xi

11.L←L⋃L″，重新训练分类器H

12.END WHILE

13.输出分类器H

令n表示输入样本集的规模。DRNG算法计算ρ的时间复杂度为O(n2)，计算δ和P的时间复杂度为O(n2)，构造原型树T的时间复杂度为O(n2)，构造近亲结点图的时间复杂度为O(n2)，计算J的时间复杂度为O(n2)，所以DRNG算法的整体时间复杂度为O(n2)。相似算法SETRED[14]算法耗时主要在于构造RNG，整体时间复杂度为O(n3)。STSFCM[17]算法耗时主要在于训练SVM，其总体时间复杂度为O(n3)。STDP[19]算法主要耗时在于计算ρ和δ，其整体时间复杂度为O(n2)。所以，DRNG与SETRED、STSFCM相比时间复杂度要小得多，而与STDP相差非常小。

3 实验结果与分析

3.1 实验设置

实验环境为Intel®CoreTMi5-8265U CPU@1.8 GHz、16 GB RAM、Win10 64位操作系统、MATALAB R2019a。实验所使用的PCA算法和NN算法均来自于MATALAB R2019a官方工具箱。

为对DRNG算法的有效性进行验证，选取了Banknote、German、Heart、Segment、COIL20、MSRA25、ORL和Palm这8个基准数据集进行实验，其中Banknote、German、Heart和Segment这4个数据集的维度较低，而COIL20、MSRA25、ORL、Palm这4个图像数据集维度较高。

在选取的8个数据集中，涵盖了样本量较大的数据集和样本量较小的数据集，涵盖了维度很高的图像数据和维度较低的非图像数据集，不同数据集的类别个数差异也很大，能够验证DRNG的有效性。表2对8个数据集详细信息进行了描述。

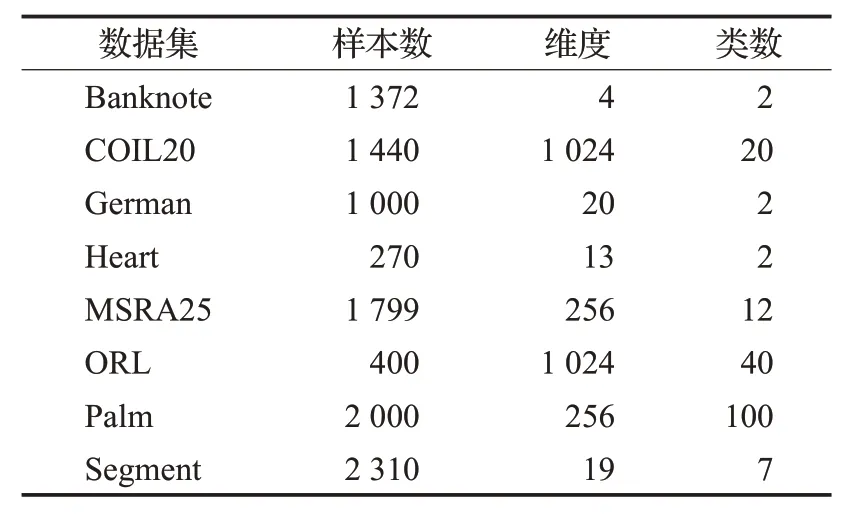
表2 数据集信息Table 2 Information of datasets

图4展示了2个图像数据集的部分数据。每个数据集各选取2个类别中的10个样本展示，每行为同一个类别。图像数据维度较高不便于进行分类实验，所以统一用PCA把图像数据降到10维，再进行实验。

对比算法选取近年来相关的Self-Training算法SETRED[14]、STSFCM[17]、STDP[19]和STDPCEW[21]，以上算法均根据原文实现。各对比算法的参数设置在表3中列出。

如表3所示，SETRED[14]和STDP[19]只有1个参数，STSFCM[17]、STDPCEW[21]和DRNG有两个参数。

图4 COIL20、MSRA25和ORL代表样本Fig.4 Representative sample of COIL20，MSRA25 and ORL

表3 参数设置Table 3 Parameter settings

3.2 实验结果分析

对选取的4个算法SETRED[14]、STSFCM[17]、STDPCEW[21]、STDP[19]和DRNG进行对比，5个算法各运行10次。分别在表2中的8个基准数据集上进行实验。

由于COIL20、MSRA25、ORL、Palm这四个图像数据维度较大，已先用PCA将其降到10维，再进行各算法对比实验。

初始有标签样本比例为10%，即训练数据集中包含10%的有标签样本和90%的无标签样本。性能评价指标选取准确率（Accuracy）和F分数（Fscore-Macro），计算10次运行结果的准确率和F分数的平均值（mean）和标准差（std）。实验结果如表4、表5所示，每个数据集上的算法性能最大值已加粗显示。

表4的实验结果表明，在所选取的Banknote、German和Heart数据集上，DRNG的准确率（Accuracy）和F分数（Fscore）值要高于SETRED、STSFCM，STDP和STDPCEW这4个算法，与排名第2的算法性能相比，DRNG的准确率（Accuracy）分别高出0.06、0.66和0.72个百分点，而STDPCEW仅在Banknote数据集上优于STDP，在German和Heart数据集明显弱于STDP，可能是因为上述两个数据集上的特征取值范围差异较大，最大近邻归一化距离权重不太适用于这种情况。在Segment数据集上DRNG的准确率分别稍低于SETRED和STDP算法0.45和0.11个百分点，但要高于STSFCM和STDPCEW。

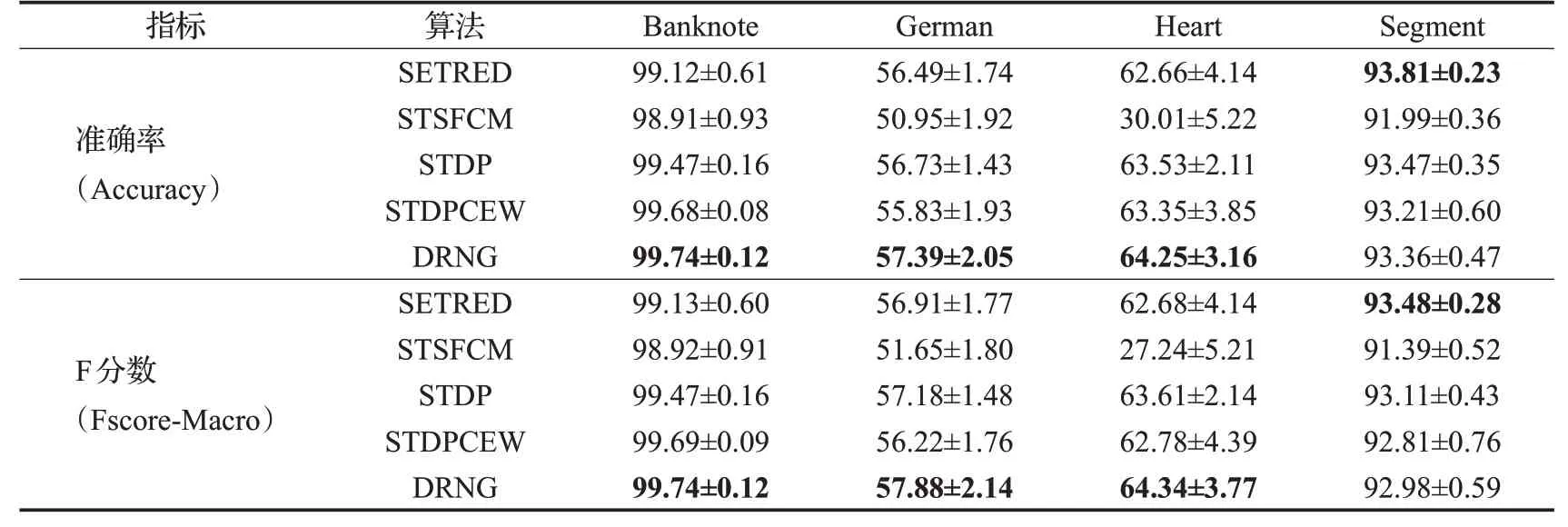
表4 各算法在Banknote、German、Heart和Segment上的性能（mean±std）Table 4 Performance of each algorithm on Banknote，German，Heart and Segment（mean±std）%

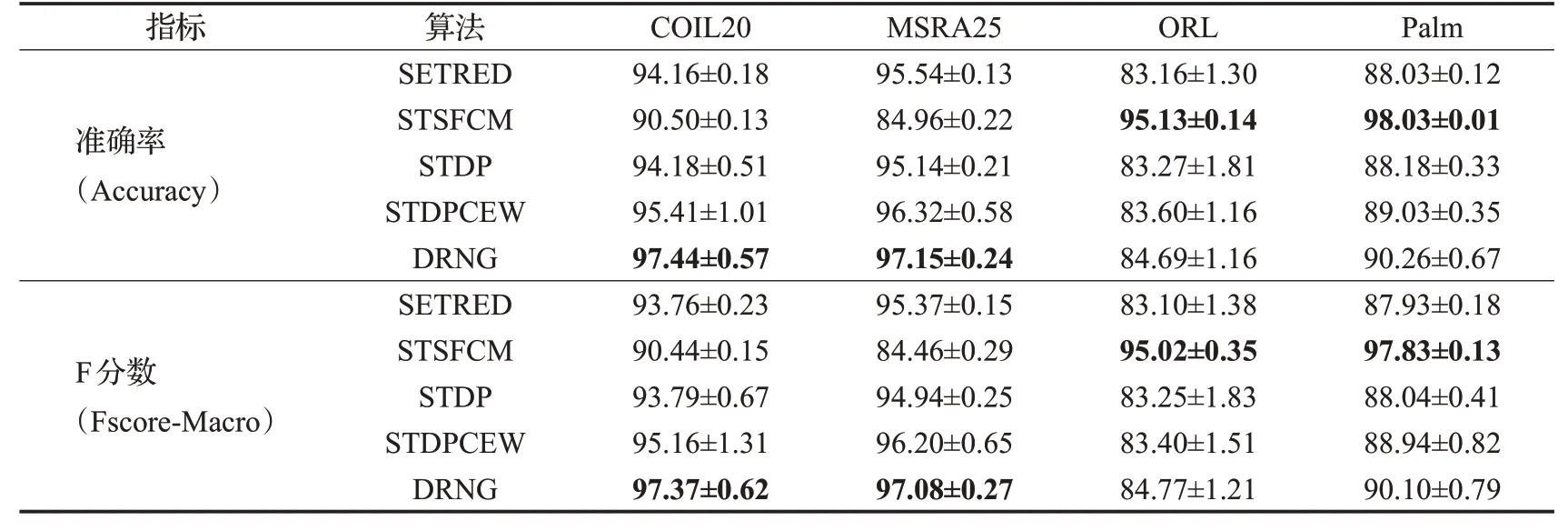
表5 各算法在COIL20、MSRA25、ORL和Palm上的性能（mean±std）Table 5 Performance of each algorithm on COIL20，MSRA25，ORL and Palm（mean±std） %

表5的实验结果表明，在COIL20和MSRA25这两个数据集上，DRNG的Accuracy和Fscore值要高于SETRED、STSFCM、STDP和STDPCEW这4个算法，与第2名相比，Accuracy分别高了2.03和0.83个百分点。而在这两个数据集上，STSFCM的性能要明显低于SETRED、STDP和STDPCEW。在ORL和Palm这两个数据集上，DRNG的Accuracy和Fscore值高于SETRED、STDP和STDPCEW，而SETRED要略微低于STDP。从表5可以看出，STSFCM算法在不同数据集上的性能差异很大，在ORL和Palm数据集上性能较好，而在COIL20和MSRA25数据集上则明显低于对比算法。在类别分布都较为平衡的情况下，Accuracy和Fscore的值趋向于一致。

对8个基准实验数据集上的实验结果综合分析可得：

（1）DRNG算法在Banknote、German、Heart、COIL20和MSRA25数据集上性能优于对比的SETRED、STSFCM、STDP和STDPCEW算法，在ORL和Palm数据集上性能低于STSFCM算法，在Segment数据集上各对比算法性能接近。

（2）DRNG算法采用原型树构建近亲图，所选择的高置信度样本点质量较高，所以，DRNG在Banknote、German、Heart、COIL20、MSRA25、ORL和Palm数据集上优于同样采用NN算法作为基分类器的SETRED、STDP和STDPCEW。

（3）DRNG算法采用NN算法作为基分类器，对类簇数比较小的数据集效果更好，而SVM算法对类簇数比较大的数据集性能更好。ORL数据集有40个类簇，Palm数据集有100个类簇，在这两个数据集上，采用NN算法作为基分类器的方法性能均低于采用SVM算法作为基分类器的STSFCM算法。实验结果与理论分析一致。

综上所述，DRNG算法利用非对称割边权重进行高置信度样本识别，能够更好地识别出高置信度样本，从而降低了自训练迭代过程中的误分类风险，提升了半监督分类性能。

3.3 运行时间分析

为对比5个算法的运行耗时，各算法以10%的初始有标签样本比例运行10次，计算出平均耗时，表6为各算法的运行时间。

表6 算法运行时间比较Table 6 Algorithm running time comparison s

从表6中的数据可以看出，总体上，STDPCEW的耗时接近SETRED，因为复杂度都为O(n3)，DRNG的耗时接近STDP，因为复杂度都为O(n2)。SETRED在小数据集Banknote、German、Heart和Segment上耗时最长，而在另外四个图像数据COIL20、MSRA25、ORL和Palm上耗时少于STSFCM。STSFCM在较大图像数据集COIL20、MSRA25、ORL和Palm上耗时最长，而在较小数据集Banknote、German、Heart和Segment上耗时仅高于STDP，STDP在所有数据集上耗时最少，DRNG耗时仅次于STDP。

3.4 参数研究

DRNG算法涉及超参数截断距离比例α和显著性水平θ。图5为准确率（Accuracy）和F分数（Fscore）随α值变化的情况。图6为准确率（Accuracy）和F分数（Fscore）随α值变化的情况。

（1）α值对分类准确度的影响

α在[0.5,5]区间内取值，步长为0.5。α对应截断距离,d为距离集合。dc的取值影响高置信度样本选取，过大会导致类簇难以划分，使近亲结点图割边数量增加，过小导致局部中心点数量过多，近亲结点过少。

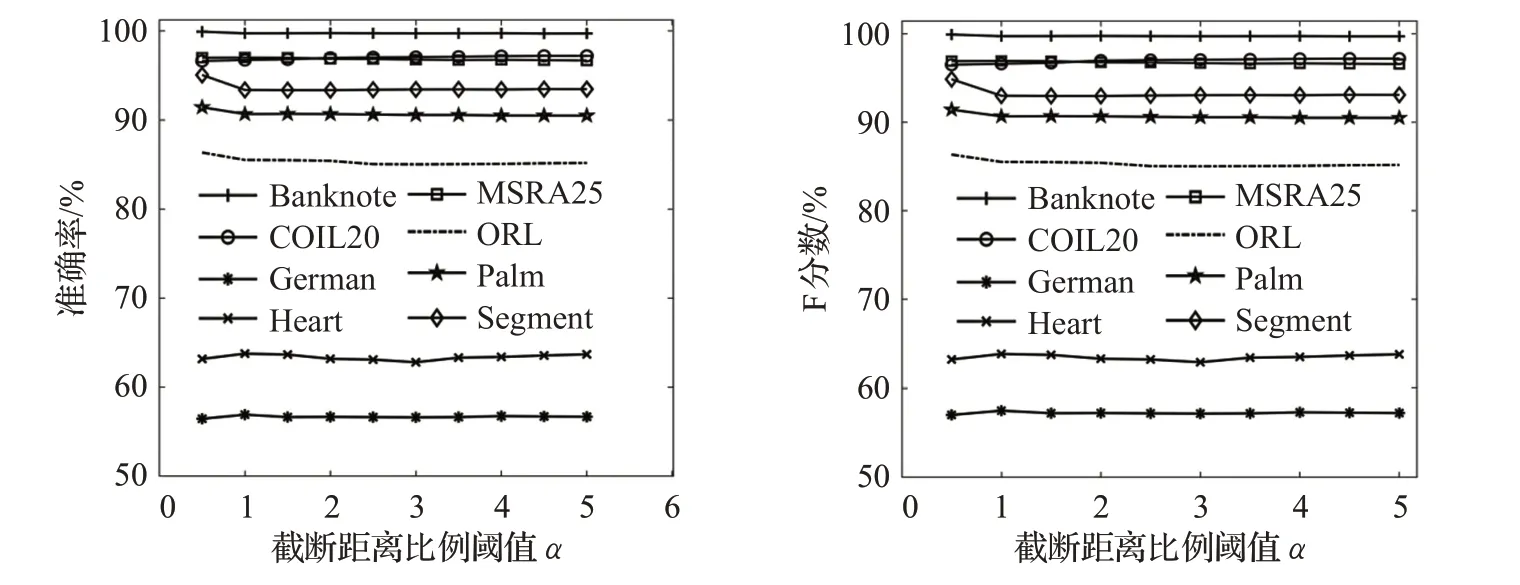
图5 α值对准确率和F分数的影响Fig.5 Effect of parameterαto Accuracy and Fscore

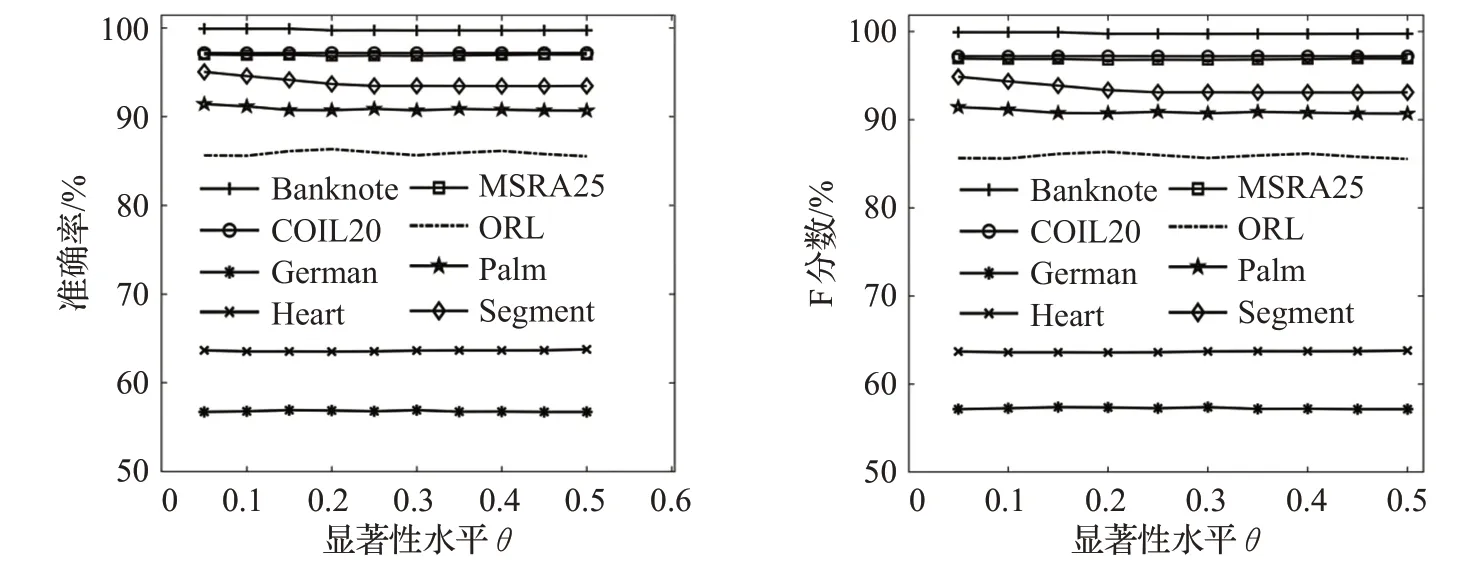
图6 θ值对准确率和F分数的影响Fig.6 Effect of parameterθto accuracy and Fscore

如图5所示，在Segment、ORL和Palm数据集上α值取0.5时分别获得了最大的分类准确率95.06%、86.35%和91.43%，而在German和Heart数据集上α值取1时分别获得最大的分类准确率63.77%和56.92%，在Banknote、COIL20和MSRA25数据集上，准确率为96.7%～97.2%。小数据集如German、Heart和ORL对dc的取值较为敏感，而大数据集如Banknote和MSRA25等对dc的取值不太敏感。根据实验经验，α的建议取值范围为[0.5,2]。

（2）θ值对分类准确度的影响

θ表示显著性水平，θ在[0.05,0.5]区间内取值，步长为0.05。θ的取值过小会使落在拒绝域内的样本点过少，每次迭代过程中获取的高置信度样本过少，会丢失一些重要的结构信息。θ的取值过大会使拒绝域范围扩大，会使高置信度样本的质量降低、误分类点增加，从而降低分类性能。

由图6可以看出，在Segment和Palm上，θ值取0.05时分别获得了最大的分类准确率95.06%和91.43%，在ORL数据集上θ值取0.2时准确率为86.35%。而Banknote、German、Heart、COIL20和MSRA25数据集对θ的取值不敏感，这是因为原型树内近亲结点已经具有较高的置信度，含有非常少的割边，利用融合密度信息的非对称割边权重检验后，即使拒绝域发生变化，Ji几乎都落在拒绝域内。根据实验经验，θ的建议取值范围为[0.05,0.2]。

4 结束语

本文提出一种近亲结点图编辑的Self-Training算法，通过密度峰值定义原型关系，并构造近亲结点图。在基分类器预测的有标签样本的近亲结点集内，定义非对称割边权重，并利用假设检验的方式来识别出高置信度样本，降低了高密度样本在Self-Training迭代学习过程中的误分类风险。在8个基准数据集上和相关的Self-Training算法进行对比实验，结果表明DRNG算法的分类性能整体上优于SETRED、STSFCM、STDP和STDPCEW。但该算法仍存在可以继续改善的地方，比如峰值和距离计算的方法，尤其是面临高维数据因采样过于稀疏而导致距离计算失效的问题，这将是下一步工作的重点。