融合Sin混沌和分段权值的阿基米德优化算法

罗仕杭，何 庆，2

1.贵州大学 大数据与信息工程学院，贵阳 550025

2.贵州大学 贵州省公共大数据重点实验室，贵阳 550025

在工程应用和科学研究中存在大量高维度、非线性以及目标函数不可导的全局优化问题，传统的优化方法很难在合理的时间内找到这些问题的全局最优解。元启发式算法具有原理简单、易操作、参数少等优点，为复杂全局优化问题提供了一种新的解决途径。因此，近年来元启发式发算法在避障[1]、自动控制[2]、调度问题[3]、图像演化[4]、路径规划[5]等领域得到广泛应用与研究。

阿基米德优化算法（Archimedes optimization algorithm，AOA）是2021年Hashim等[6]基于阿基米德原理提出的新型元启发式优化算法，AOA的种群个体是浸入流体中的物体，当浸入流体中的物体之间发生碰撞时，碰撞程度随时间不断减弱，适应度值优的个体加速度大，引导其他个体逐渐收敛到最优位置，达到寻优的目的。

AOA具有模型简单、易于扩充、设置参数少等优点。然而，AOA与其他群智能优化算法相似，存在全局搜索能力弱、寻优精度低、易陷入局部最优等缺陷。

为改善群智能算法存在全局搜索能力弱、寻优精度低、易陷入局部最优等问题，许多学者提出改进：王坚浩等[7]针对鲸鱼优化算法（whale optimization algorithm，WOA）收敛精度低的问题，添加惯性权重对种群位置进行非线性扰动更新，提高了算法的收敛精度；龙文等[8]提出非线性变化的收敛因子，达到平衡WOA的全局探索和局部开发能力；李守玉等[9]将变异反向学习策略引入蝴蝶优化算法（butterfly optimization algorithm，BOA），提高算法的寻优精度；王海瑞等[10]将柯西高斯变异引入麻雀搜索算法（sparrow search algorithm，SSA）中，在增加种群多样性的基础上避免算法陷入局部最优。虽然上述文献中的改进策略在一定程度上提高算法收敛精度和速度，但是算法仍存在全局开拓能力弱、搜索精度不足等缺陷。为此，本文提出融合Sin混沌和分段权值的阿基米德优化算法（SAOA）。首先，利用无限折叠迭代的Sin混沌反向学习策略初始化种群，通过计算适应度值选取初始阶段最优的个体，增强种群多样性并提高求解效率；其次，引入算数交叉算子，将当前个体与最优个体进行交叉，产生的子代个体更靠近全局最优个体，引导种群向最优区域靠拢，增强全局搜索的充分性；同时，采用分段权值策略来平衡算法的全局开采和局部挖掘能力，协助算法跳出局部最优。最后通过8个基准测试函数及其Wilcoxon秩和检验、部分CEC2014测试函数以及机械优化案例进行仿真实验，验证了SAOA的有效性和可行性。

1 阿基米德优化算法

在标准AOA中，通过转移因子(TF)控制个体间碰撞和平衡状态之间的切换（即算法从全局探索切换到局部开发的过程）获得优化问题的解，其中定义如下：

式中，t表示当前迭代次数，tmax表示迭代次数。

在初始化阶段，AOA初始化个体的密度(den)、体积(vol)、加速度(acc)，在此步骤中，AOA评估初始化种群，选出当前最优适应度个体位置(xbest)、最优密度(den)、最优体积(vol)、最优加速度(acc)，以此用来对下一代密度、体积和加速度的更新。

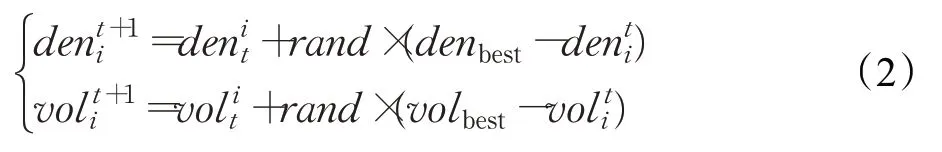
式中，N是种群的规模，i=(1,2,…,N)。rand是取值为（0，1）的随机数。和分别为第i个个体在第t代和第t+1代的密度，和为第i个个体在第t代和第t+1代的体积。

当TF≤0.5时，算法进行全局搜索，个体的加速度更新方式如下：

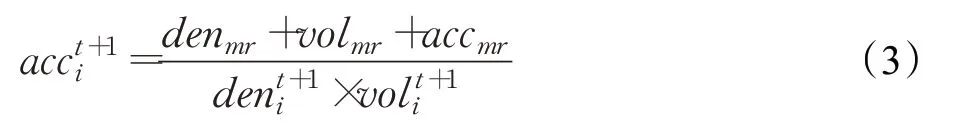
当TF＞0.5时，算法处于局部开发阶段，此时个体加速度更新公式为：

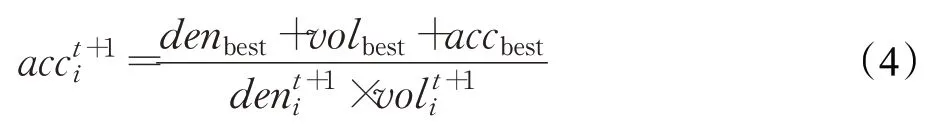
通过公式（5）对加速度进行标准化处理，用来进行个体位置更新：

式中，u和l为常数。

在全局搜索阶段，碰撞个体的位置更新公式如下：

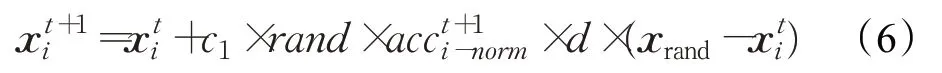
式中，表示第i个个体在第t次迭代的位置向量，C1为常数，rand∈(0,1)的一个随机数，xrand表示第i个随机个体在第t次迭代的位置向量，d为密度降低因子，更新公式为：

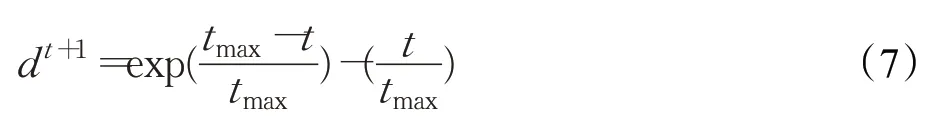
在局部开发阶段，个体的位置更新公式为：

式中，xbest表示全局最优个体，C2为常数，T=C3×TF,C3为常数。F是改变个体移动方向的标志，用于决定个体位置更新的方向，定义如下：

式中，p=2×rand-C4,C4为常数。

2 改进的阿基米德优化算法

在基本AOA中，种群初始化采用随机分布的方式，这种方式造成种群多样性差，导致个体前期搜索存在一定的盲目性，从而使得算法收敛速度慢；其次，在全局开发阶段，AOA仅依靠随机个体带领种群向最优区域寻找最优解，当随机个体是一个较差的解时，会导致算法求解精度低，同时，在局部开发阶段，虽然种群围绕最优个体进行位置更新，但是当最优个体陷入局部极值空间时，种群也会陷入局部最优，使得算法出现停滞搜索现象；最后，AOA用来平衡全局搜索和局部开发能力的转移因子TF并不是有规律的，根据公式（1）可知TF的最小取值是0.36，最大值是1，则全局搜索阶段的区间是（0.36，0.5），局部开发阶段的区间是（0.5，1），这使得算法全局搜索阶段过短，未能搜索更广阔的区域，可能丢失更优的解。

综上所述，本文针对上述AOA原理的缺陷，引入对应的策略进行改进。具体策略介绍如下。

2.1 Sin混沌反向学习初始化策略

种群初始多样性可以有效地扩大算法的搜索范围，从而提高算法的寻优精度和收敛速度[11]。混沌经常被用于优化问题，其基本原理是通过映射关系在混沌变量空间[0，1]之间产生混沌序列，再将其转化到个体的优化变量空间内。Sin混沌模型是一种具有较好遍历性和随机性的映射折叠次数无限的混沌模型。反向学习[12]通过当前解寻到其对应的反向解，然后评估选择更好的解，从而引导个体寻找最优解。因此，本文先利用Sin混沌产生多样性较好的初始种群；其次，根据反向学习产生反向种群；最后，分别计算Sin混沌初始种群及反向种群的适应度，选择适应度低的解作为初始种群，提高了找到最优初始解的概率，从而使种群向全局最优解靠近。Sin混沌1维映射表达式如下：

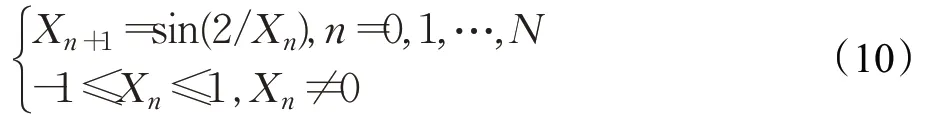
式中，Xn是取值为(-1,1)的序列且初始值不能设置为0。将Sin混沌序列映射到解空间中，得到种群X={Xi,i=1,2,…,N},Xj={Xj,j=1,2,…,dim}，种群个体表示如下：

式中，Xi+1,j为第i+1个种群的第j维值。

由种群X计算反向种群,，反向种群个体表示如下：

式中，[Xminj,Xmaxj]为搜索空间的动态边界。将Sin混沌种群X和反向种群X*组成新种群{X∪X*}，将新种群的适应度值进行排序，选择N个适应度值最优的个体组成初始种群。

2.2 算数交叉算子

在标准的AOA中，碰撞个体根据公式（6）进行全局搜索，由于没有任何先验条件可以使用，仅依靠种群中随机个体的引导进行种群位置更新，随机个体可能是一个质量较好的解，也可能是一个较差的解，导致算法的全局寻优性能较弱。因此，为提高标准AOA的全局搜索性能，本文引入的算术交叉算子，表达式如公式（13）所示：

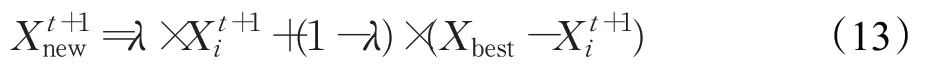
式中，λ∈(0,1)表示随机数。

SAOA选择当前个体与全局最优个体进行算术交叉，产生新的子代个体更靠近当前最优解，从而加快群体向全局最优区域靠拢，同时算术交叉算子给予当前个体向优秀个体学习的能力，增强种群信息分享能力，从而增加种群多样性。将当前个体与全局最优个体进行交叉后，虽然能增强算法全局搜索能力，但是无法直接判断产生的新个体是否优于原始个体。因此，通过交叉选择后，利用贪婪机制比较新旧个体适应度值，再决定是否更新当前个体，通过这种方式不断获得更优解，从而提升算法全局寻优性能。其中贪婪机制的数学模型如公式（14）所示：

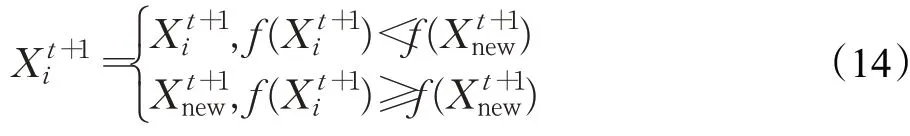
2.3 分段权值策略

在标准AOA中，转移因子TF取值为（0.36，1），当TF＞0.5时，算法进行局部开发，最优个体引导种群进行位置更新，但是当最优个体陷入局部极值空间时，种群将受其影响陷入局部最优，使得算法出现“早熟”现象。为解决这个问题，本文提出分段权值的位置更新策略，首先，借鉴双曲正切函数的思想，本文在算法迭代前中期种群位置更新处引入动态双曲正切权值w，其值随迭代次数的增加呈非线性递减，其次，在算法迭代后期，引入正弦波动权值，降低算法陷入局部最优的概率。本文所采用的动态双曲正切权值，在算法迭代前期，SAOA获得较大权值以保证其在更广阔的区域搜索最优解，在算法迭代中期，SAOA获得较小权值，使当前个体可以在最优个体附进行精确搜索，达到平衡全局搜索与局部开发的能力，算法迭代后期，利用正弦波不规则变换的特点来增强最优个体在局部空间开发的多元性，协助种群跳出局部最优。分段权值w的计算如公式（15）所示：

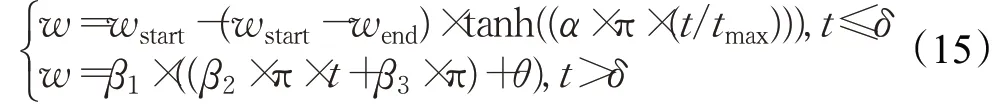
式中，wstart表示迭代开始时的初始权值，即当t=0时，wstart=0.8,wend表示迭代结束时的权值，即当t=tmax,wend=0.4。δ为迭代次数，β1=0.23,β3=1.6,θ=0.3。α和β2为调节因子，控制曲线的平滑度，经过多次实验验证，当α=0.75和β2=0.06时，实验结果为最优。

由图1可知，在算法迭代初期，w值较大，使SAOA具有较强的全局勘探能力，在算法迭代中期，w值较小，使SAOA的开发性能逐步提高并尽可能在最优解附近精确寻优，在算法迭代后期，w值的方向和大小变换的不确定性增强SAOA搜索的多元性，避免算法陷入局部极值空间。因此，AOA引入分段权值策略后全局搜索阶段的个体位置更新公式为：

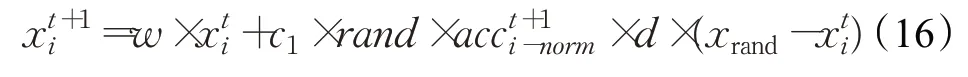
局部开发阶段个体位置更新公式为：

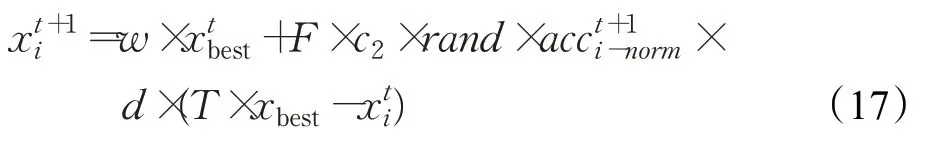
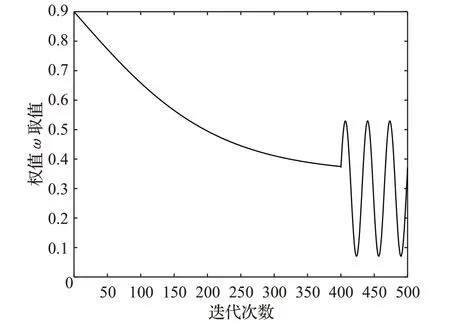
图1 分段权值曲线图Fig.1 Segmented weight curve graph

2.4 SAOA算法实现步骤

综上改进策略，本文所提的SAOA算法步骤如下：

步骤1初始化算法相关参数：种群规模N、空间维度dim、种群的搜索空间[ub,lb]、最大迭代次数tmax、参数C1、C2、C3、C4、密度(den)、体积(vol)、加速度(acc)。

步骤2采用Sin混沌反向学习初始化策略初始化种群。

步骤3计算种群中每个个体的适应度值并记录当前最优个体位置(xbest)、最优密度(den)、最优体积(vol)、最优加速度(acc)。

步骤4根据公式（1）、（2）、（7）分别更新函数TF、den、vol、d。

步骤5当TF≤0.5时，进入步骤6根据公式（3）更新函数acc，进一步根据公式（5）更新函数acci-norm；当TF＞0.5时，进入步骤7，根据公式（4）更新函数acc，进一步根据公式（5）更新函数acci-norm。

步骤6算法进行全局搜索，根据公式（13）选择随机个体与当前最优个体进行算术交叉操作，产生新的候选解，并通过公式（14）进行扰动，进一步根据公式（16）更新个体位置。

步骤7算法进行局部开发，根据公式（17）更新个体位置。

步骤8判断是否满足迭代终止条件，满足则输出全局最优解及位置信息，否则进入步骤3继续执行。

改进算法流程图如图2所示。

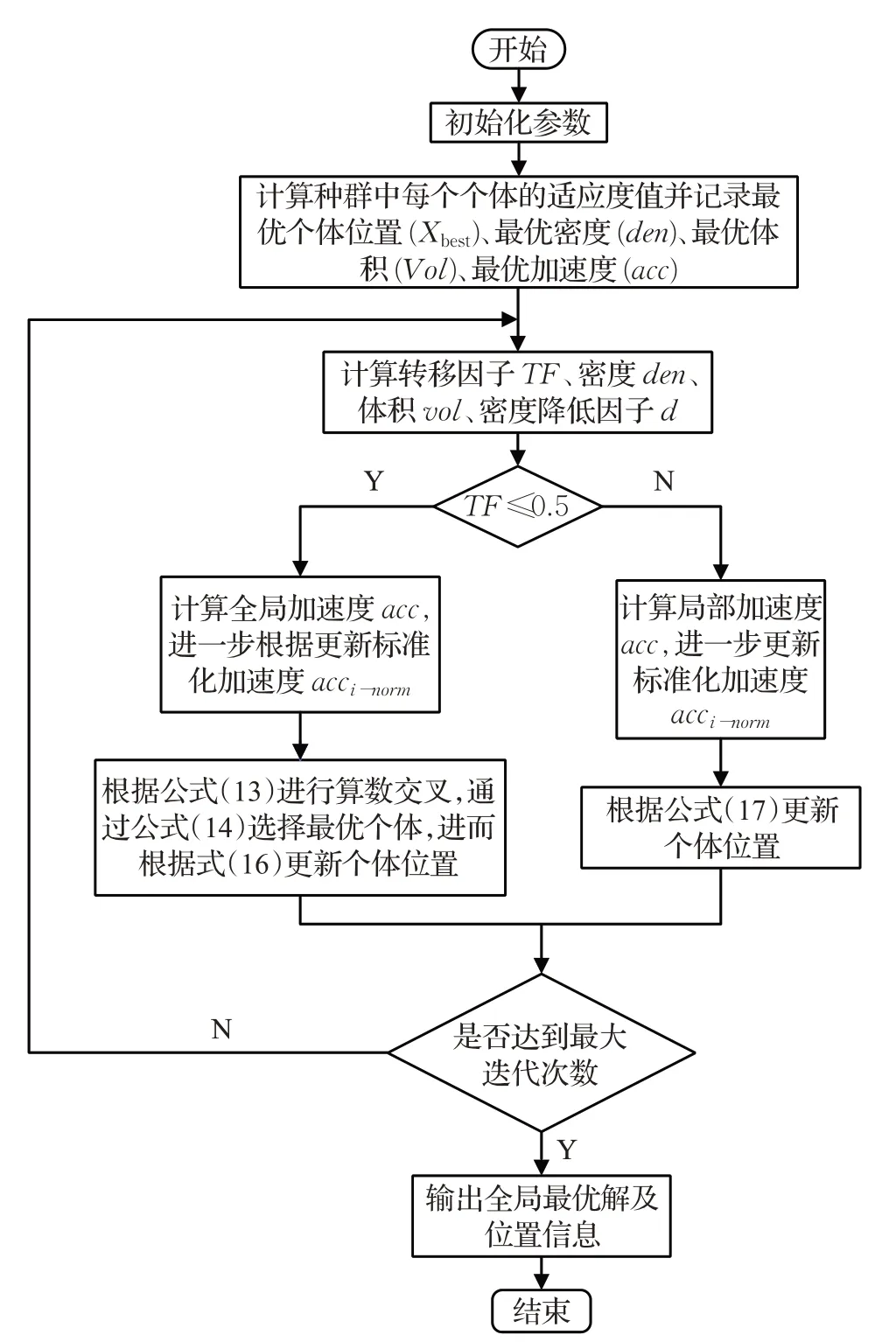
图2 SAOA算法流程图Fig.2 SAOA algorithm flow chart

2.5 SAOA时间复杂度分析

时间复杂度间接反映算法的收敛速度。在标准AOA中，假设参数初始化（种群规模N、维度d等参数）时间为η1，初始化每个个体需要的时间为η2，求解目标适应度函数时间为f(d)，则标准AOA种群初始阶段时间复杂度为：

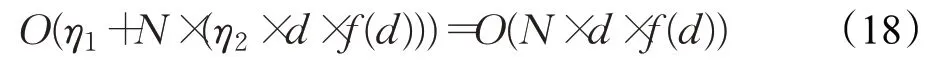
设更新函数TF、den、vol、d、acc时间为η3，每一维按公式（6）和（8）更新位置所需时间为η4，比较当前位置和历史最优位置的时间为η5，选取最优位置的时间为η6，此阶段时间复杂度为：

所以基本AOA的时间复杂度为：

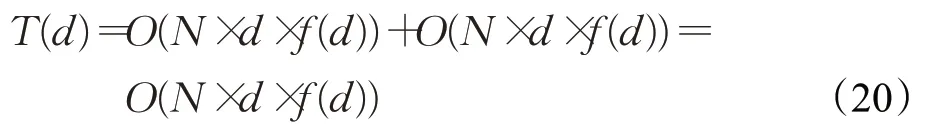
在SAOA中，初始化参数所需时间与基本AOA相同，采用Sin混沌反向学习初始化种群所需时间为复杂度为O(N×d×f(d))，则SAOA初始化种群阶段的时间复杂度为：

计算算术交叉算子所需时间为η7，每一维按公式（13）进行个体位置更新，利用贪婪机制比较新旧个体适应度所需时间为η8，保留最优位置时间为η9，此阶段的时间复杂度为：

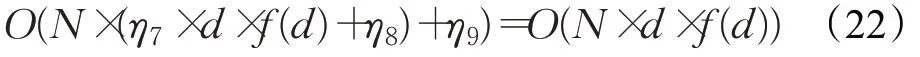
算法引入分段权值后，每一维按照公式（16）和（17）更新个体位置所需时间为η10，此阶段的时间复杂度为：

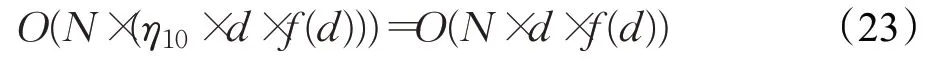
综上分析可得，SAOA的时间复杂度为：

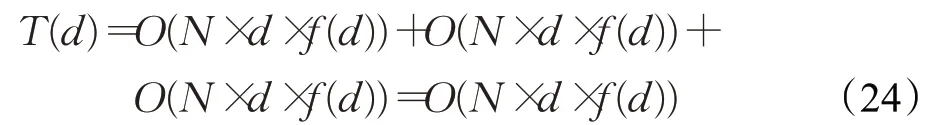
综上所述，SAOA与AOA时间复杂度一致，本文针对AOA缺陷所提改进策略并没有增加时间复杂度。

3 仿真实验与结果分析

3.1 实验设计与测试函数

本文基于Intel®CoreTMi7-i7-6500U CPU，2.50 GHz主频，8 GB内存以及Windows 10（64位）的操作系统对所提出的算法进行仿真实验。编程软件为MATLAB 2018（a）。各个算法的参数设置如表1所示，选取8个基准函数其中5个单峰函数F1～F5，3个复杂非线性多峰函数F6～F8，取值范围、最优值信息如表2所示。

表1 算法参数设置Table 1 Algorithm parameter setting

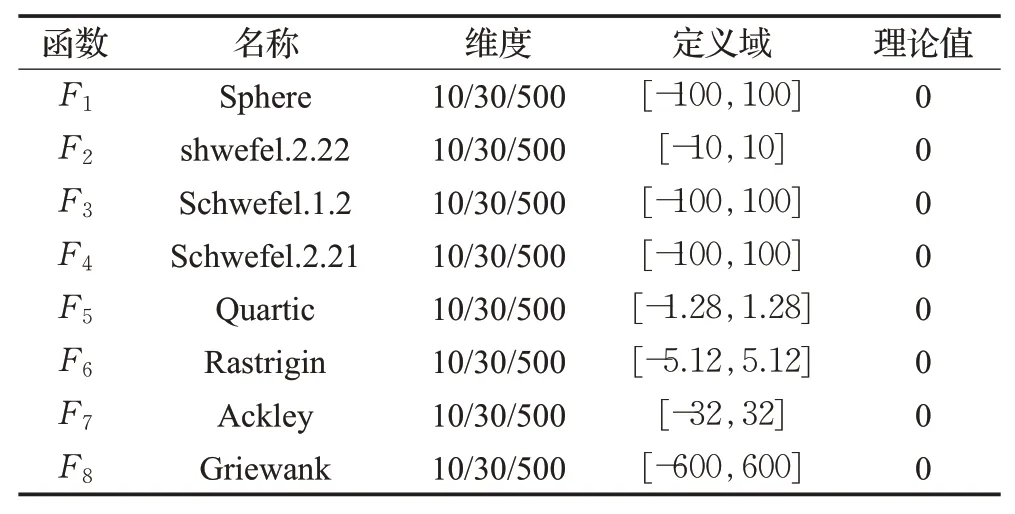
表2 基准测试函数介绍Table 2 Benchmark test functions

3.2 不同改进策略对算法性能影响分析

为验证SAOA算法的可行性和优越性，将基本AOA与本文加入Sin混沌反向学习初始化策略的算法（AOA1）、加入算术交叉算子的算法（AOA2）、加入分段权值策略的算法（AOA3）在8个具有不同寻优特征的基准函数上进行仿真实验。算法参数统一设置为：种群规模N=30,搜索空间维度dim=30,最大迭代次数tmax=500。表3通过最优值、最差值、平均值和标准差四个性能指标来评估各算法的寻优性能。5种算法对8个基准测试函数的寻优结果如表3所示。

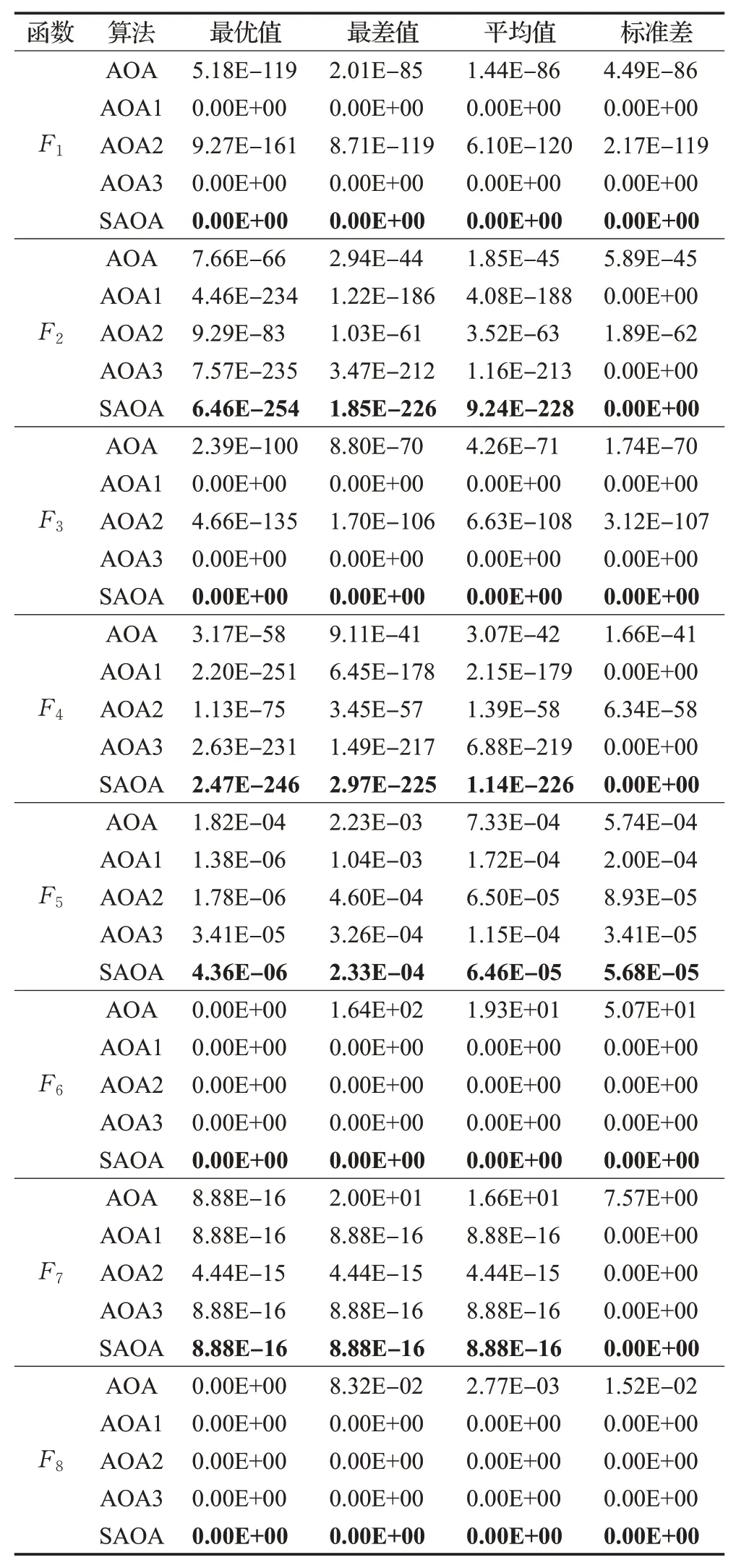
表3 不同改进策略的结果比较Table 3 Comparison of results of different improvement strategies

由表3可知，SAOA对函数F1、F3、F6、F8求解时，SAOA都能够寻到理论最优值，对函数F2和F4，无论是寻优精度还是稳定性均表现出明显的优势。在求解函数F5和F7时，SAOA陷入局部最优值，其他对比算法也寻优停滞，但SAOA相较于其他改进策略具有更高的收敛精度和稳定性。具体来说，仅采用算术交叉算子（AOA2）对AOA性能的改进有限，但其收敛精度相对于AOA也得到一定程度的提升，尤其对求解函数F6和F8，均得到了寻优理论值，这是因为通过当前个体与最优个体进行交叉后，不仅增强种群之间信息交流，而且产生的子代个体可以有效引导种群向最优区域进行寻优。Sin混沌反向学习初始化策略（AOA1）和分段权值策略（AOA3）对函数F1、F3、F6、F8效果显著，均能寻到理论值，同时对函数F2、F4求解精度和稳定性也有极大提升，这是因为Sin混沌反向学习初始化策略增强了种群的多样性并提高初始阶段种群解的质量，分段权值策略使得算法在迭代前期获得较高权值，增强SAOA全局探索能力，在迭代中期权值减小，帮助SAOA在局部空间精确搜索，在迭代后期权值大小和方向不断变化，协助SAOA跳出局部最优，提高算法的寻优精度和收敛速度。

3.3 算法收敛性分析

为了反映SAOA的动态收敛特性，取搜索空间维度为30维，每个算法独立运行30次，采用平均收敛曲线图描述算法的收敛性。图3（a）～（h）给出了8个基准测试函数的平均收敛曲线图：

由图3可知，对于函数F1、F2、F3、F4、F6、F8,SAOA在寻优精度和收敛速度上都明显优于其他4种对比算法，且迭代前期的搜索性能和迭代末期的开拓性能也都优于其他4种算法，在相同的迭代次数下具有更高的求解精度和更快的收敛速度，并在相同的求解精度下具备更快的收敛速度，表明SAOA在保证开拓能力的同时也能充分保证搜索能力，不失种群多样性和寻优稳定性。对于函数F5、F7,SAOA与其他4种算法一样，虽然陷入局部最优后难以跳出，但SAOA的平均收敛曲线均位于4种对比算法平均收敛曲线下方，且达到特定精度所需的迭代次数最少。

综上，表3的实验结果与图3的平均曲线验证了本文所提改进算法的有效性。虽然在某些函数上5种算法收敛精度差距不明显，但SAOA的收敛速度远快于其他对比算法，表明SAOA的综合寻优能力比其他算法更强，稳定性更高。

3.4 与最新改进的群智能算法对比

为比较SAOA与其他改进算法的寻优性能，本文将SAOA与新改进的灰狼算法（improved grey wolf optimizer for solving engineering problems，IGWO）、混合灰狼和布谷鸟搜索优化算法（hybrid grey wolf and cuckoo search optimization algorithm，GWO_CS）、新改进的鲸鱼算法（CWOA）、IWOA以及新改进蝴蝶优化算法（PWBOW）在空间维度30/200/500条件下对8个基准测试函数进行仿真实验，其中“—”表示参考文献未给出相应数据，每个算法独立运行30次后结果如表4所示。

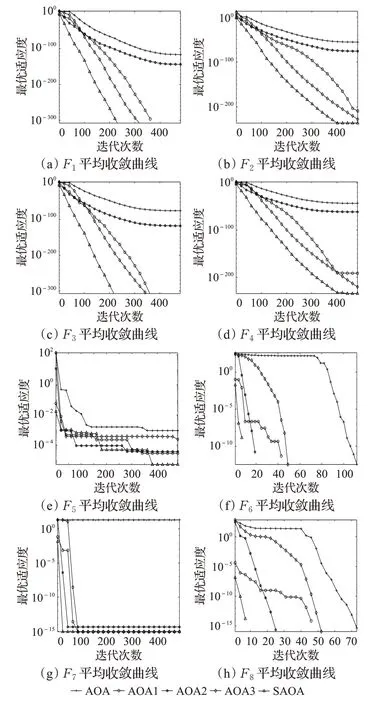
图3 5种算法的平均收敛曲线图Fig.3 Comparison of average convergence curves of 5 algorithms

由表4的实验结果表明：总体上IGWO与GWO_CS寻优能力相差不大，CWOA是5种对比算法中寻优精度最高的，且SAOA求解精度和稳定性明显优于5种对比算法。

从纵向来看，CWOA只有对函数F1、F6、F8求解时，才能找到理论值，且由标准差可知CWOA寻到理论值不具有稳定性，对函数F1～F4，IGWO算法与GWO_CS算法无法求解且PWBOA求解精度不高时，SAOA仍具有较高的寻优精度和稳定性，其中IGWO求解精度是5种算法中最差的，GWO_CS算法次之。函数F5存在局部极值，算法容易陷入局部最优且无法跳出，CWOA对其求解精度略优于SAOA，但差异稳定在同一个数量级内，可以接受。函数F7是一种具有山脊形状的多峰函数，其全局最优值比较难寻，所以SAOA同其他改进算法均未找到理论值，但其寻优精度和稳定性均高于其他算法。

表4 与三种改进群智能算法在不同维度的结果对比Table 4 Comparison with results of three improved swarm intelligence algorithms in different dimensions

从横向来看，当维度从30维上升到200维再上升到500维，5种对比算法求解精度和鲁棒性均有不同程度下降，这是因为随着维度增加使基准函数复杂度增加，寻优过程需要更多计算，但SAOA求解精度仍最高，从而验证了SAOA在求解低维和高维问题时具有极强的鲁棒性，进一步说明了SAOA在求解函数优化问题时具有一定的竞争优势。

3.5 Wilcoxon秩和检测

上诉仿真实验中，仅凭平均值和标准差不能够完全说明SAOA算法的优越性。为了保证算法的公平性和有效性，需要进行统计检验[13]。本文采用Wilcoxon秩和检验验证SAOA每次实验结果是否在统计上与其他算法存在明显差异。秩和检验在5%的显著性水平下进行，当p＜5%时，可以被认为拒绝H0假设，说明两种算法之间存在显著性差异；p＞5%时，可以被认为接受H0假设，说明两种算法寻优性能上整体相同。表5给出了SAOA与AOA1、AOA2、AOA3、GWO_CS算法、IGWO算法进行8个基准测试函数上的Wilcoxon秩和检验对比分析，其中“N/A”表示两者之间性能相当，“Na”表示不适用，即无法进行显著性判断，判断结果，“+”“-”“=”分别表示SAOA性能优于、劣于和相当于对比算法。由表5可知，大部分p值都小于5%，总体上SAOA的性能与其他6种算法在统计上差异显著，从而表明SAOA比其他算法拥有更好的优越性。

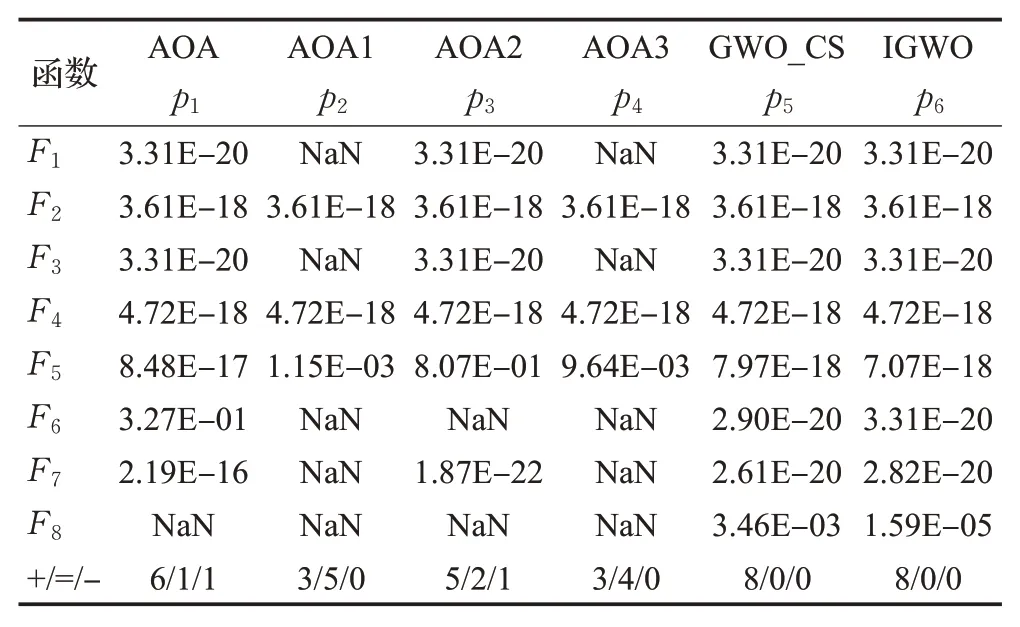
表5 Wilcoxon秩和检验结果Table 5 Wilcoxon rank sum test results

3.6 在CEC2014测试函数上进行测试

为了进一步验证SAOA处理具有复杂特征的问题时的鲁棒性，本文选取部分具有复杂特征的CEC2014单目标优化函数进行优化求解，其中包括单峰（CEC01）、多峰（CEC12）、混合（CEC19）和复合（CEC23、CEC27、CEC30）类型函数，选取的部分函数如表6所示。本文将SAOA与基本AOA、PSO算法、GWO_CS算法、PWBOA、IGWO算法进行实验对比。其中L-SHADE算法在CEC2014函数中表现出色，常作为对比算法，其数据和PSO算法的数据来源于文献[14]。实验参数选取种群规模为30，最大迭代次数为1 000，维度为30，独立运行30次取平均值和标准差，实验结果如表7所示。

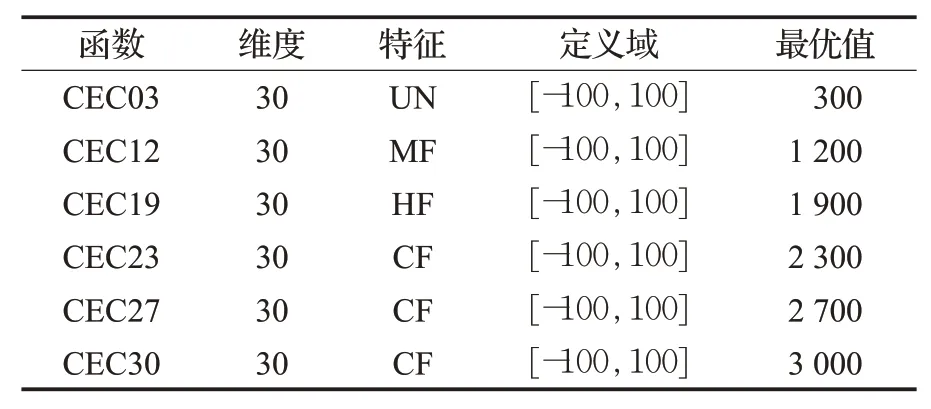
表6 部分CEC2014函数介绍Table 6 Part of CEC2014 function

如表7可知，L-SHADE在单峰CEC03函数上表现出色，而SAOA寻优性能相较标准AOA弱一些，因为SAOA需要进行更多的参数计算，造成收敛精度稍有下降；在多峰CEC12函数和在混合CEC19函数上，SAOA寻优精度更加接近理论值；在复合特征CEC23、CEC27和CEC30函数上，SAOA的标准差为0，说明其对于复合特征函数寻优稳定性强。上述CEC2014测试函数寻优结果分析说明，本文提出的SAOA算法对于具有复杂特征的函数寻优上同样具有很大优势，验证了SAOA算法具有较强的鲁棒性。

4 仿真实验与结果分析

优化设计是20世纪60年代发展起来的一门新学科与设计方法。在机械优化设计中，经常需要解决数值优化问题，然而传统的优化方法受限于目标函数是非线性和可微等问题，很难找到最优的解决方法[15]。因此，本文将提出的SAOA用于求解机械优化设计问题，进一步验证所提算法的适用性和可行性。

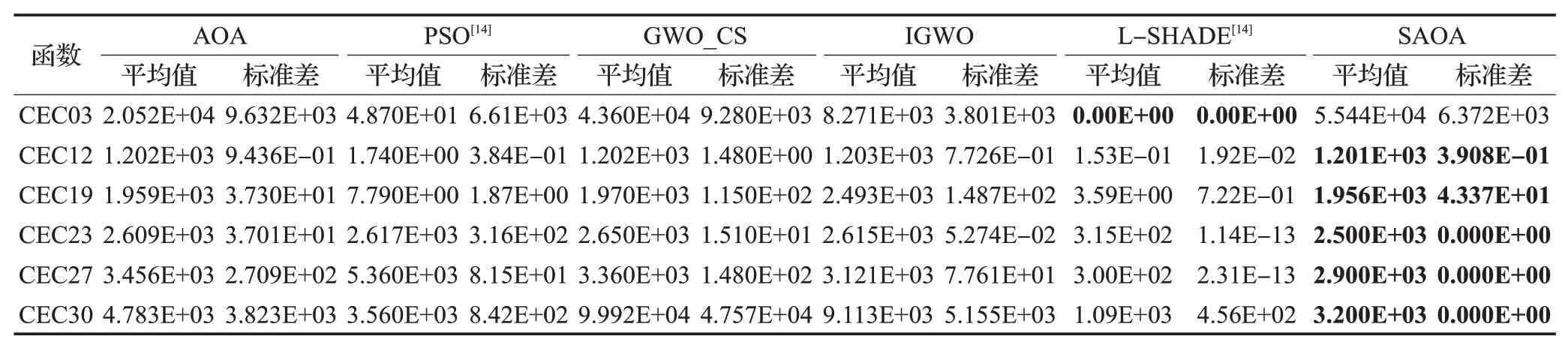
表7 CEC2014函数优化对比Table 7 CEC2014 function optimization comparison

绝大多的机械优化问题与数学模型有着紧密的联系。选择设计变量，目标函数以及约束条件是构造优化设计数学模型的关键步骤。该问题的数学模型一般可以描述为如下约束优化问题[16]：

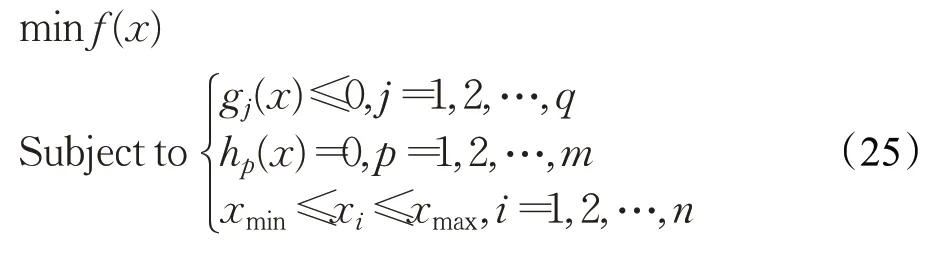
式中，x为设计变量，f(x)为目标函数，gj表示第j个不等式约束，hp表示第p个等式约束，xmin和xmax分别表示设计变量的上下界。

焊接梁设计是机械优化设计问题中的一种，其设计是在4个决策变量和7个约束条件下，以最小化焊接梁的制造费用为优化目标。决策变量分别为焊缝厚度(h)、钢筋连接长度(l)、钢筋高度(t)和钢筋厚度(b)，其结构示意图如图4所示。

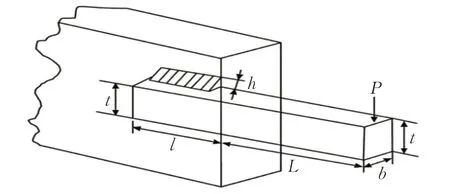
图4 焊接梁结构示意图Fig.4 Schematic diagram of welded beam structure

焊接梁设计的数学模型如下所示。

目标函数：

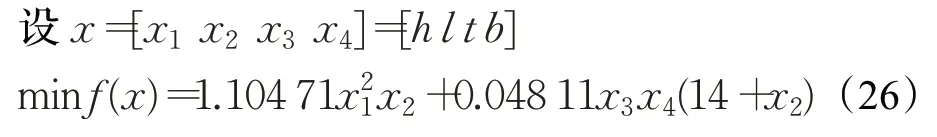
约束方程：

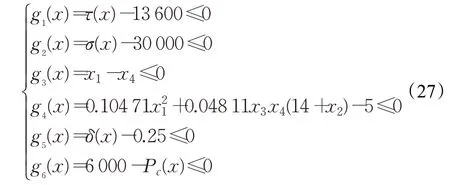
其中：

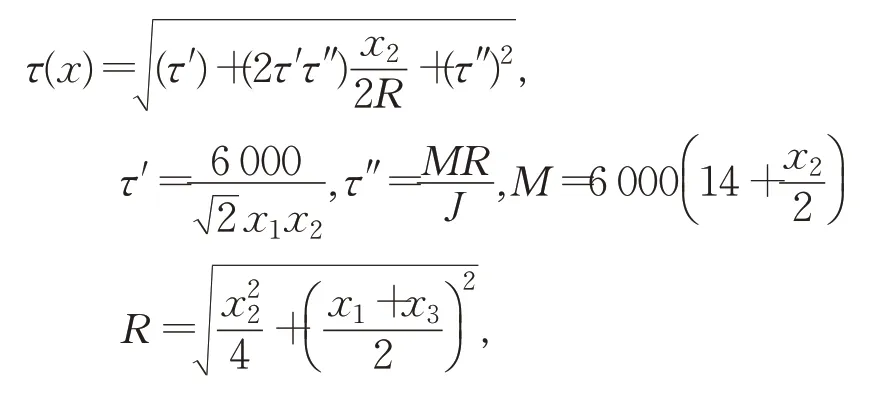
式中，τ为剪切应力，σ为横梁弯曲应，Pc为屈曲载荷，δ为横梁挠度，f(x)为最小化设计费用总成本。

为了保证实验对比的公平性，与文献[6]参数一致，选取种群规模为30，最大迭代次数为1 000，每个算法独立运行30次，其中SCA、WOA、PSO算法、EO算法的数据来源于文献[6]。表8是SAOA与其他算法求解焊接梁设计的实验对比结果。

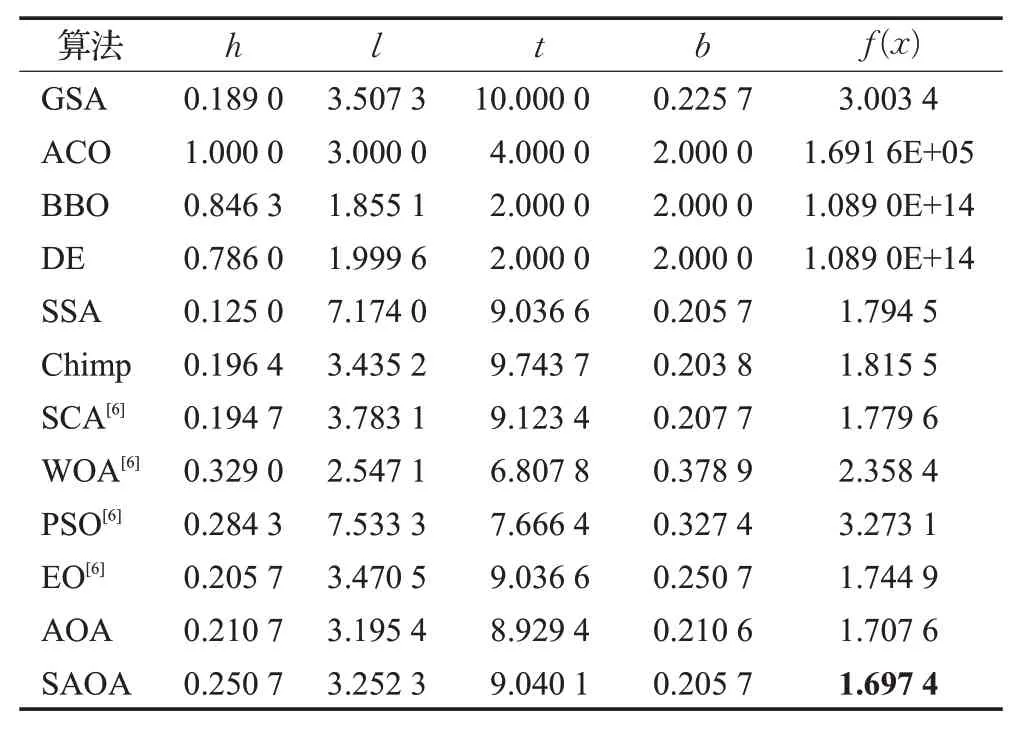
表8 不同算法求解焊接梁设计问题的对比结果Table 8 Comparison results of different algorithms for solving welded beam design problems

由表8可知，通过焊接梁设计问题的实例验证，所提SAOA可以取得优于其他算法的优化结果，说明SAOA寻优能力优于其他算法，具有较好的求解精度，进一步验证SAOA在实际应用中的可行性和适用性。

5 结束语

为了改善AOA的性能，本文提出融合Sin混沌和分段权值的阿基米德优化算法，首先采用Sin混沌反向学习策略初始化种群，提高了初始种群的质量；其次引入的算术交叉算子，增强算法的全局寻优性能；同时在算法中加入分段权值平衡算法全局探索和局部开发能力，降低算法陷入局部最优的概率。通过8个基准测试函数和部分CEC2014测试函数仿真实验以及基准测试函数Wilcoxon秩和检验结果证明提出的SAOA具有更好的寻优性能和有效性。最后，将SAOA应用到机械设计案例中，进一步验证该算法的可行性和适用性。下一步研究内容的重点内容是将SAOA应用到更加复杂的工程中，如多目标优化、高维函数优化问题等。