一种多步的基于切换星间测量的多星自主导航算法

周博超，李勇

中国空间技术研究院 钱学森空间技术实验室，北京 100094

1 引言

分布式卫星系统是由物理上互不相连的、共同实现同一空间任务的多颗卫星构成的空间系统，是21世纪空间技术发展的新趋势[1-2]。分布式卫星系统的应用任务要求其具有自主协同运行的能力，其中的核心和基础便是自主导航，传统的单卫星导航一般依赖于地面站或全球导航星座系统，而基于星间测量的自主导航系统能够不依赖外部支持，主要通过星间相对测量信息，利用非线性估计理论解算出卫星间的相对运动状态参数和卫星各自的惯性姿态参数，具有自主性强、占用资源少等优点。

基于星间测量的自主导航按测量方式可分为基于星间测距[3]、基于相对视线角测量[5-7]和基于星间相对位置矢量测量[8-9]的导航方法。分布式卫星系统中卫星之间的相对矢量需要距离、角度及姿态同时测量才能获得，故在卫星较多的情况下，所有卫星间均进行测量会需要大量的敏感器。本文从星载资源优化的角度出发，采用单一敏感器切换测量的方案，即仅有一颗卫星搭载测量设备，轮流对其他卫星进行测量的方案。文献[10]表明，3颗星的情况下，切换测量的误差约为全测量误差的1.8倍左右，但减少了一半的观测设备，精度也是可以接受的。

在单敏感器切换测量的方案下，导航计算将全部由测量设备所在的导航星来完成。为了减小导航星的运算负担，将卡尔曼滤波算法解耦为多个平行的子滤波器是一种有效的解决方案[11]。这种解耦算法将卡尔曼滤波解耦为两个平行的滤波[12]，由于维数的减小，运算负担能够有效地减轻。文献[13]提出了一种最优的两步滤波法，并证明了该算法与卡尔曼滤波为数学等价的，之后文献[14]将其推广为多步滤波法,该算法得到了广泛的应用[15-17]。为了减轻导航星的运算负担，本文考虑采用多步滤波算法，将标准EKF(extended Kalman filter，扩展卡尔曼滤波)算法解耦为多个6维子滤波器，即以每颗星的状态作为一个子系统，由于该算法与标准卡尔曼滤波数学上完全等价，故可以在保证相同滤波性能的同时有效减轻计算负担。

文章首先给出切换导航方案；然后建立系统的状态空间模型并根据标准EKF算法给出滤波过程；基于多步卡尔曼滤波算法将原滤波器进行解耦，给出解耦后子滤波器及耦合项的方程，并对算法的计算量进行了评估；最后给出仿真验证。

2 切换导航方案

本文以3颗卫星构成的分布式卫星系统为例，采用惯性空间相对位置矢量作为观测量的自主导航方法进行定位。假设3颗卫星分别为卫星A，卫星B和卫星C，rAB，rBC，rAC分别是3颗卫星间的相对位置矢量(质心到质心矢量，如图1所示)。根据基于星间矢量测量的双星导航的能观性分析[4,18]可知，3颗卫星之间的任意两个相对位置矢量测量(除特殊轨道情形外)即可解算出整个卫星系统在惯性空间中的位置和速度。由于测向设备一般无法保证同时跟踪测量多颗卫星的方位信息，所以需要两套测量设备分别进行观测或者一套设备在两卫星之间进行切换观测。

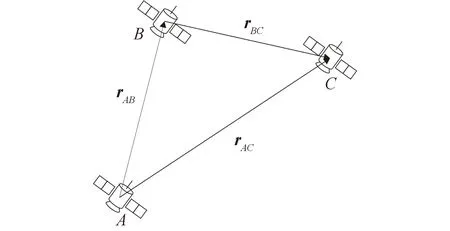
图1 星间位置矢量Fig.1 Inter-satellite position vectors

本文从减少测量载荷节约成本的角度出发，提出采用单套测量设备切换观测的方案，即仅在卫星A上配置一套测量设备，在卫星B和卫星C之间进行切换测量。

3 系统模型

选取地心赤道惯性坐标系下3颗卫星的位置向量和速度向量组成系统状态变量，记

x为18维状态变量，则二体轨道下的系统状态方程为

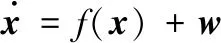
(1)

式中：

μ=3.986 004 415×1014m3/s2；w为系统噪声。 观测量是卫星间相对位置矢量，相应的观测方程为

(2)

式中：σ=1,2，分别代表测量B星及C星；v为量测噪声；Hσ为对应的测量矩阵，

4 滤波算法

4.1 标准EKF算法

对于基于星间矢量的自主导航，一般所用的方法为EKF算法。对如式(1)(2)所描述的切换系统，标准EKF的计算步骤为[9]：

xk/k-1=f(xk-1/k-1)

(3)

(4)

(5)

xk/k=xk/k-1+Kk(yk-Hσkxk/k-1)

(6)

Pk/k=[I-KkHσk]Pk/k-1

(7)

式中：Q阵及R阵分别为系统噪声及测量噪声的方差。

4.2 多步卡尔曼滤波算法

基于文献[14]中的MSKF (multi-stage Kalman filter，多步卡尔曼滤波)算法，将标准EKF算法解耦。该方法的核心是将方差阵Pk/k-1及Pk/k变换为分块对角阵，即找到上三角阵Uk，Vk使得：

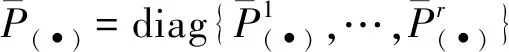
(8)

(9)

利用该UV矩阵，可将标准EKF算法进行如下变换：

(10)

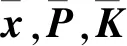
(11)

(12)

综合(3)～(7)(10)(11)可得变换后的滤波方程如下：

(13)

(14)

(15)

(16)

(17)

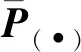
(18)

(19)

其中：

ε(·)为单位阶跃函数，即εt=1(t≥0)，εt=0(t<0)。 于是将式(13)～(17)展开，可得解耦后的子滤波器:

(20)

(21)

(22)

(23)

(24)

其中i=1,2,…,r为子滤波器编号，式中变量含义如下：

耦合项Uk，Vk更新方式如下：

(25)

(26)

式中：

(27)

以上就是变换后的解耦的子滤波器方程，注意变换后的滤波器估计的状态及方差阵为U-V变换后的量，而原变量的估计需由下式反变换计算得来：

子滤波器的初值为：

解耦的多步滤波算法与标准的EKF为等价推导的，这是由于多步滤波算法本质上为标准EKF算法经过变量代换(U-V变换)后进行计算而得来，详细推导过程可见文献[14]。

5 计算量评估

为了评价多步卡尔曼滤波的计算量优势，采用“浮点运算数”(FLOPS)来描述算法的运算复杂度。

标准EKF的计算量为[14]

flops(EKF)=6n3+(4m+3)n2+(4m2+

4m+2)n+2m3+m2+m

而多步滤波算法的计算量包括子滤波及耦合项计算两部分。

而本文中n=18,m=r=3,代入可得：

flops(EKF)=40 818

flops(MSKF)=flops(Subfilters)+

flops(Auxiliary)=5 364+15 000=20 364

因此解耦后的计算量为原滤波器的49.9%。

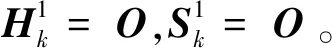
6 算例仿真

6.1 MSKF性能验证

为验证多步滤波法的性能，考虑一个由3颗卫星构成的分布式卫星系统，3颗卫星的轨道根数如表1所示。

表1 轨道根数

3颗卫星的仿真轨迹由二体开普勒方程积分而得。由仿真的轨迹可以计算出仿真星间矢量测量。测量为由A轮流测量其与B及C的相对位置矢量，切换方式为时间切换，50 s切换一次。

仿真中加入了系统及测量噪声，二者互不相关，且其方差阵满足

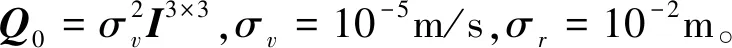
er=

ev=

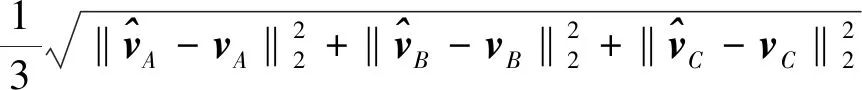
表2 MSKF与EKF仿真结果

从结果中可以看出，两种算法的精度几乎完全相同，微小差距是由Matlab浮点计算误差积累而来，但由第3部分可知MSKF的计算量要比EKF算法小得多，因此对于承担导航计算的导航星的计算负担有很大的减轻作用。

6.2 非理想切换的影响

本文的分时段切换量测过程在实际应用中必然存在测量时延和时间同步问题，各阶段测量的持续时间会不规律且会存在空档期，这对估计精度势必会带来影响，下面是对这种情况的一些简单的仿真分析。

算例1 每种测量为50 s，但切换存在5 s延迟，即每110 s为一个周期，0～50 s测量B星，55～105 s测量C星，中间的空档没有任何测量。

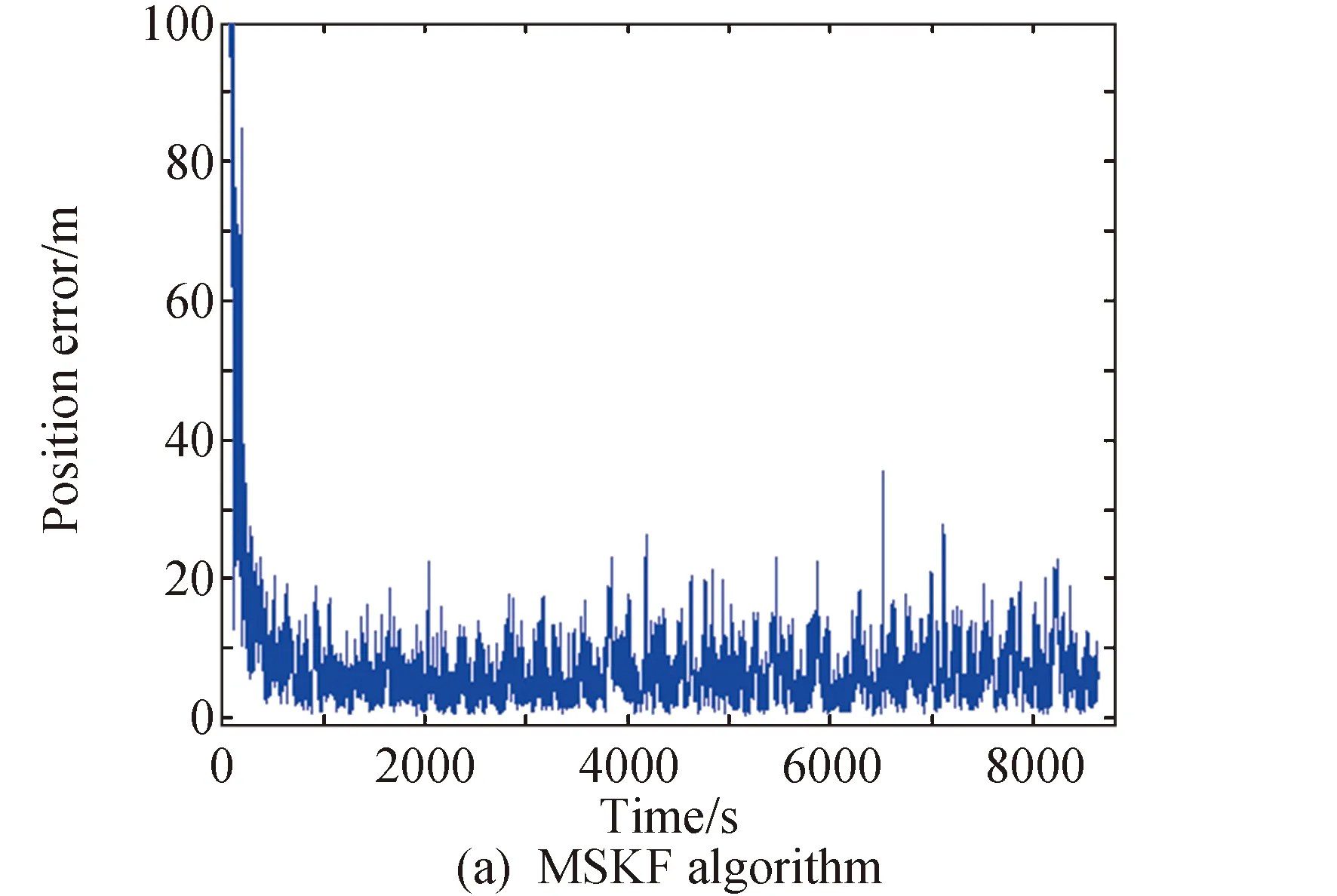
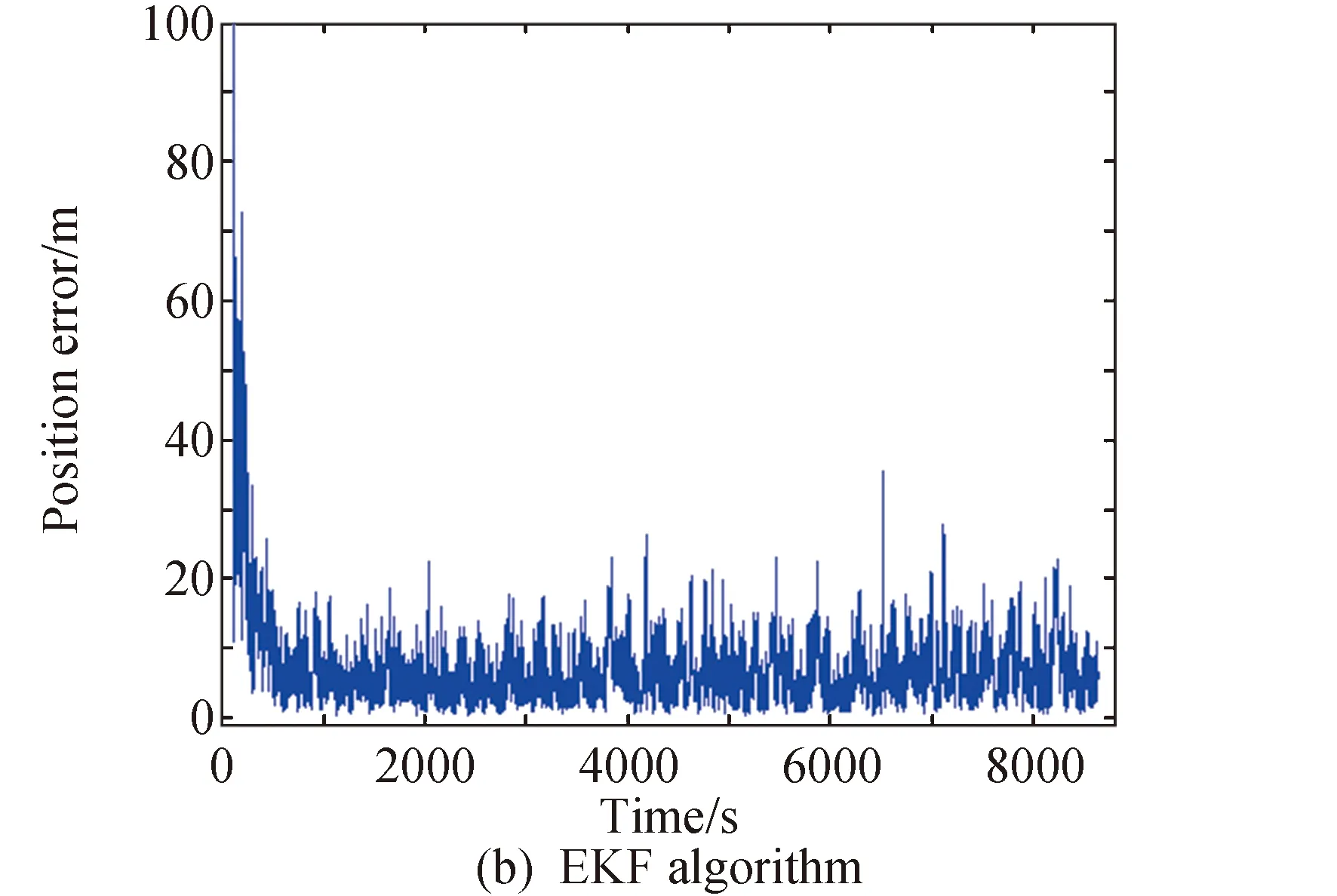
图2 两种算法位置误差Fig.2 Position error of two algorithms

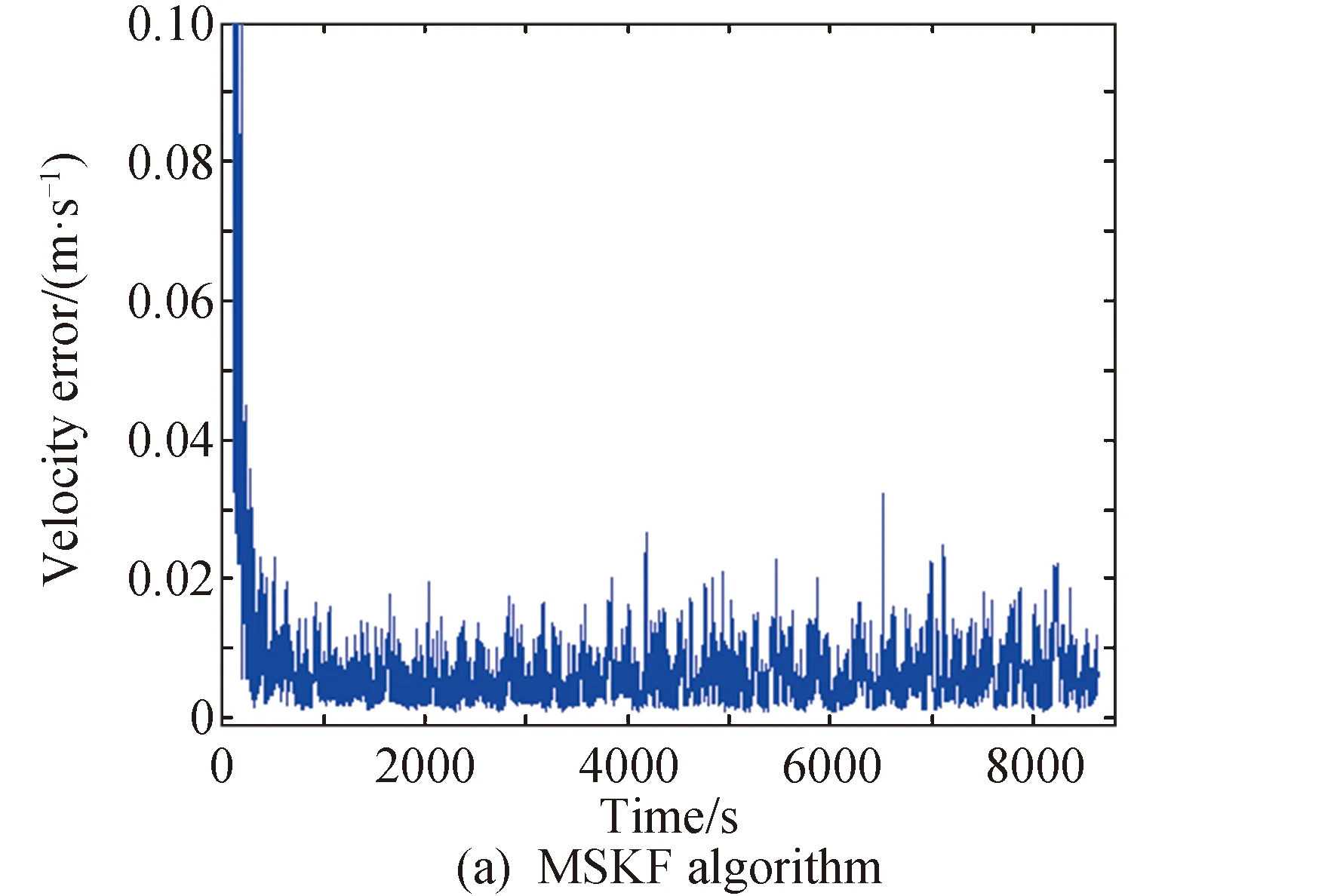
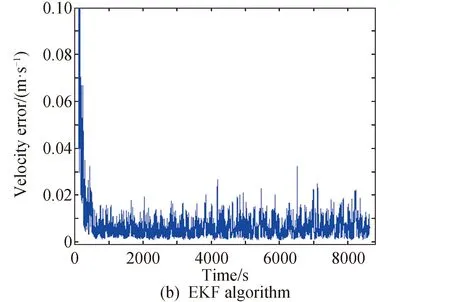
图3 两种算法速度误差Fig.3 Velocity error of two algorithms

算例2每种测量为50 s，切换存在15 s延迟。

算例3每种测量50 s，没有切换延迟，作为对比算例。

各算例中卫星数据及滤波参数均与第6.1小节中的仿真一致，仿真结果如图4及表3所示。

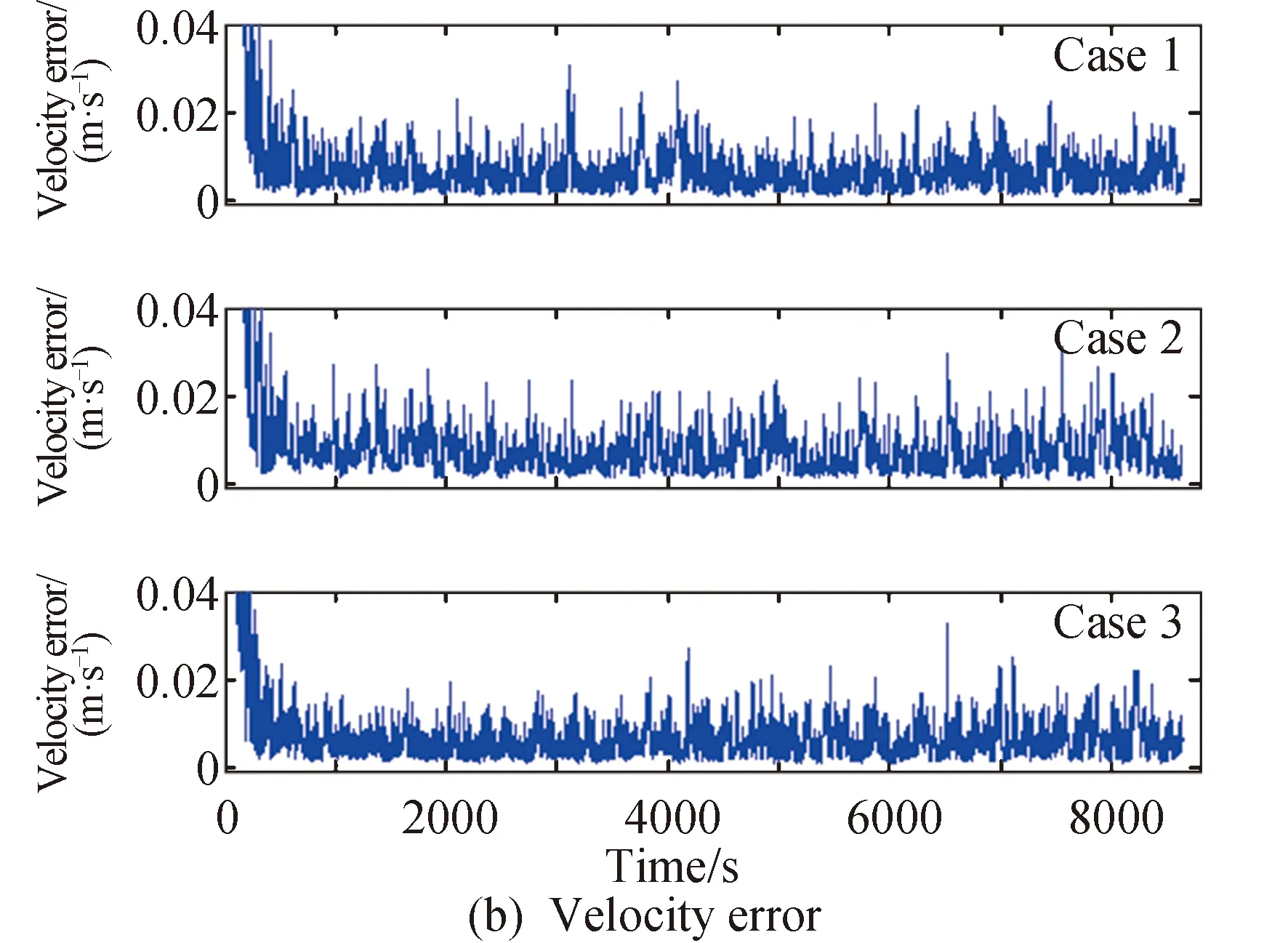
图4 三种算例的估计精度Fig.4 Estimation error of three cases

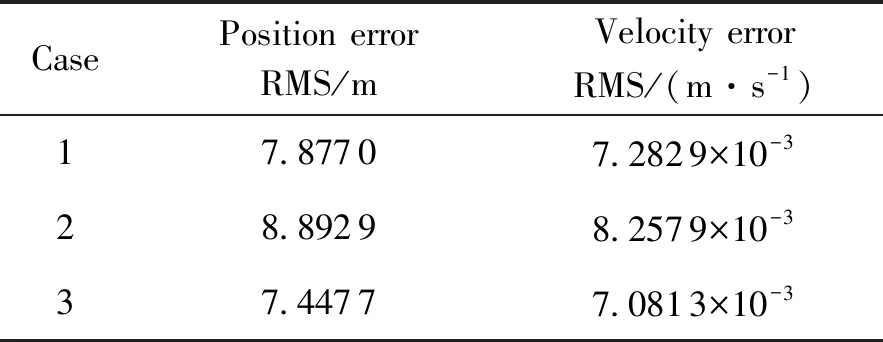
表3 非理想切换仿真结果

从仿真结果可以看出，切换时延、空档的加入降低了估计精度，时延越大估计精度越差。但实际工程中可能存在的时延和空档时间比较小，对精度影响较小，没有量级或成倍地增大。

7 结论

针对基于星间测量的多星自主导航问题，提出了一种单套敏感器切换测量的导航方案，设计了一种解耦的多步滤波MSKF算法，通过数学推导及仿真分析，得出以下结论：

1)MSKF与标准EKF为完全数学等价，即两种算法的估计值及估计精度几乎完全一致，微小差异是由舍入误差而来。

2)MSKF的计算效率相比标准EKF有显著 的提升，计算量仅为EKF的49%，在本文的切换测量下还有进一步的减轻。这对于承担导航计算的卫星计算效率有明显提升，具有重要的应用价值。

3)切换时延、空档的加入降低了估计精度，时延越大精度越差。但实际工程中可能存在的较小的时延和空档时间对精度影响较小。未来会对这种切换方案进行深入的分析，对切换系统能观性、时延的影响、切换方案设计进行进一步的探讨。