基于G/H 极值约束的马尾松人工林自稀疏规律

2022-07-20杨盛扬曾思齐张会儒谌红辉龙时胜

中南林业科技大学学报 2022年5期

杨盛扬，曾思齐，张会儒，谌红辉，龙时胜

（1. 中南林业科技大学林学院，湖南长沙 410004；2. 中国林业科学研究院华北林业实验中心，北京 102300；3. 中国林业科学研究院热带林业实验中心，广西凭祥 532600）

林分生长主要受林分密度、立地质量和林龄三个因子的影响，林分密度是人工林经营最重要的可控因子之一而备受关注[1-2]。林分密度之所以成为重要因子，是由于林分密度是林业工作者能够用以干预林分生长发育的主要因子[3]。促使林业工作者去创新的一个理由是，我们需要一种可信赖的测量林分密度的方法，通过控制树木间的竞争来增加林分的产量。如果说试图在林业科学甚至是植物生态学中确认一种单项的进步，则正确地测量林分密度的能力最有可能是其候选项[4]。

林分密度指数和自稀疏规律是林分密度管理的重要理论基础。林分密度指数方程和自稀疏方程都用来描述过度拥挤纯林的自稀疏现象，因此其本质二者是一致的[5]。

Reineke 对处于完满立木度的同龄林调查得到的数据进行分析，经验地得出林分株数与平均胸径的关系为lnN=k+alnD，他进一步研究完满立木度的不同树种组成林分的N∝D关系后发现，它们的最大密度线具有相同的斜率（b=-1.605），并且与年龄和立地无关，而参数k则因树种而异，得到完满立木度林分的N、D的关系为N=aD-1.605（N为单位面积株数；D为林分平均直径；a为常数）[6]。

林分密度指数方程自提出以来，引起学术界的广泛兴趣，也受到多方面的质疑。质疑者认为，密度指数方程主要缺点是忽略了树高因子（H），在林分发育的过程中，N与Dg成反比，而N与H成正比[7]。

Yoda 等[8]在研究草本植物时发现了一个与R方程相似的植物平均质量（W）与密度的关系，进而提出了著名的-3/2 法则（也叫自稀疏法则）。其表达式为W=kN-3/2，转化为对数形式方程，为：lnW=k-(3/2)lnN，Yoda 等所提出的-3/2 法则是基于植物生长是几何相似的理论（同速生长）。二十世纪七八十年代，公式的通用性引起生态学界的广泛注意，并得到高度评价。法则的提出得到了许多人的支持，并且被认为是“植物种群生态学中的一个最一般的原理”，因为这个法则不仅对许多陆生植物适用，同时还可应用到水生植物[9-12]。

在受到高度评价的同时，国内外学者也围绕自稀疏问题开展了大量的研究，并得出一些不同的结论。反对者从法则本身、原始数据选择、引发的机制、统计方法等方面对法则进行质疑，发现其经验证据不足，有些假设不成立[9,13-14]。有的学者基于异速生长理论提出了一些模型，然而他们得出的斜率却不等于-1.5[15-16]。有的学者研究得出，自稀疏的斜率是随着种而变化的[17-19]。Zeide[20]在对不同立地质量上生长的松树调查分析后发现，立地质量影响自稀疏指数。他认为立地条件好时，斜率比较陡，条件差时，就相对比较平缓，进一步研究得出：密度在较长时间内按-3/2法则减少，但当平均生长量达到极大值时曲线的斜率由-3/2 变成了-1，此时W＝c/p，或Wp=c(c为常量)，Wp 恒等于单位面积产量[21]。

其他学者根据不同的假设，得出不同的结果。如West 等[22]对自稀疏机理的解释，Weiner 等[23]提出自稀疏是由于个体为竞争光而产生的假说。其理论基础是林分中的“非对称竞争”，即相邻个体间相互影响的效果与它们的尺寸不成比例。当光成为植物生长的限制性资源时，非对称性竞争最可能发生。

Zeide[20]进行了不同资料来源的几个树种的实例研究，其结果解释了斜率b是一个变量而不是一个常数，它随树种和立地系统而改变，而不仅仅是围绕一个常数波动，并且提出了一个林分自忍性的测度指标（-dv/dN），并建议在确定林分疏伐强度、造林密度以及其他对纯林的管理活动中应该考虑这个指标。

自从自稀疏法则被接受以来，人们发现其斜率并不是其所表示的那样为常数，而是有很多变动的，这种观察到的变动性已经导致对法则基础有效性和存在性的质疑，以致最后支持对它的排斥[13,20,24]。同速生长模型并没有作为自稀疏规则的一般性解释而被接受，因为很多物种的生长并不是同速的，而异速生长模型受到批评是因为其预测的指数显著偏离-3/2，这看起来与经验常数-3/2 不一致[25]。因此，最大密度理论、自稀疏机理及其参数的变化规律，仍然是值得深入研究的理论问题。李凤日等[26]建议采用同一林分的林木大小及林木株数之间的动态变化规律，重新建立林分密度理论。

本研究的目的是在对马尾松林分树高、直径与断面积生长关系分析的基础上，探讨马尾松林分自稀疏的原因、方向和自疏率，以期为马尾松人工林的合理经营提供理论依据。

1 数据收集与研究方法

1.1 数据来源

数据材料1 引自文献[27]，其样地设置于中国林业科学研究院热带林业实验中心伏波实验场，地处22°10′N、106°50′E，平均海拔550 m，平均年气温19.9℃，年平均降水量1 400 mm，属南亚热带季风气候区。1989 年1 月用1 年生的马尾松裸根苗定植，试验采用随机区组设计，试验小区面积为600 m2(20 m×30 m)，设计的4 个处理为2.0 m×3.0 m（1 667 株/hm2）、2.0 m×1.5 m（3 333 株/hm2）、2.0 m×1.0 m（5 000 株/hm2）、1.0 m×1.5 m（6 667 株/hm2），试验区分别用A、B、C、D 表示，立地指数为20。材料1 的林分概况见表1。

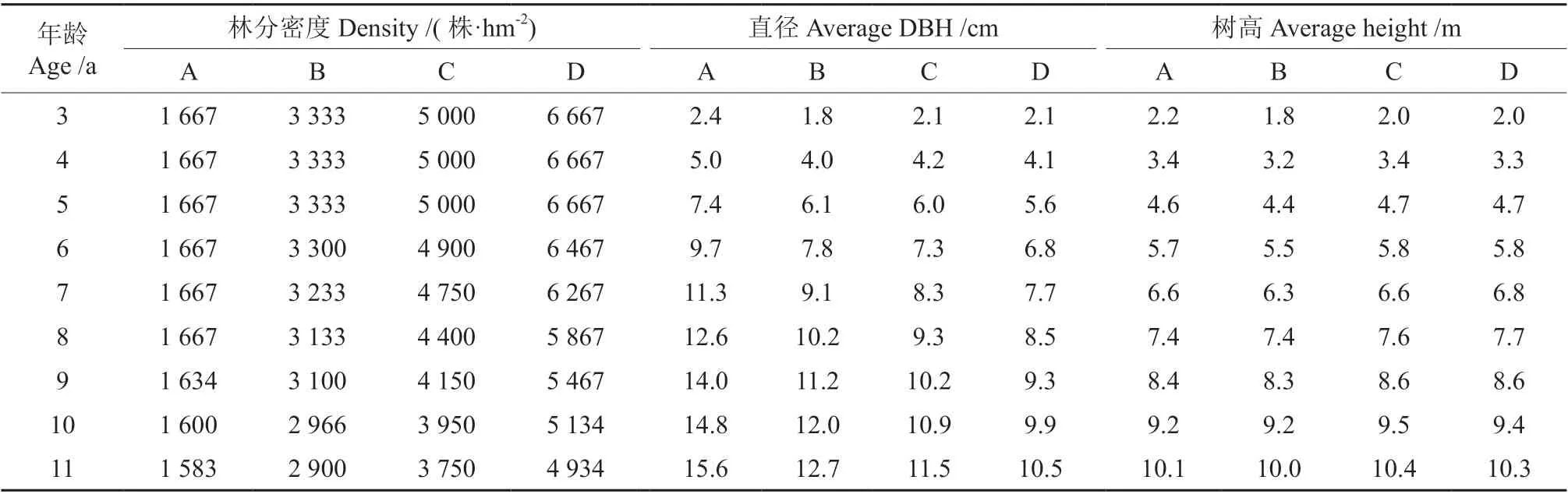
表1 马尾松不同造林密度林分因子的生长过程Table 1 The growth process of Pinus massoniana stands with different planting densities

数据材料2 取自福建省顺昌县埔上国有林场，地处26°56′N、117°47′E，平均海拔300 m，平均年气温18.5℃，年平均降水量1 880 mm，属亚热带海洋季风性气候。土壤为红壤，低山丘陵地貌。设置临时样地4块，样地内进行每木检尺，对角线测高，测定3株优势木的平均高，计算林分平均直径和平均高；每块样地选取优势木解析木和平均木解析木各1株。各样地编号分别为E、F、L、J。各样地调查时保存株数密度分别为900、780、1 200、920 株/hm2，立地指数分别为18、18、18、14，试验材料2 的林分概况见表2。

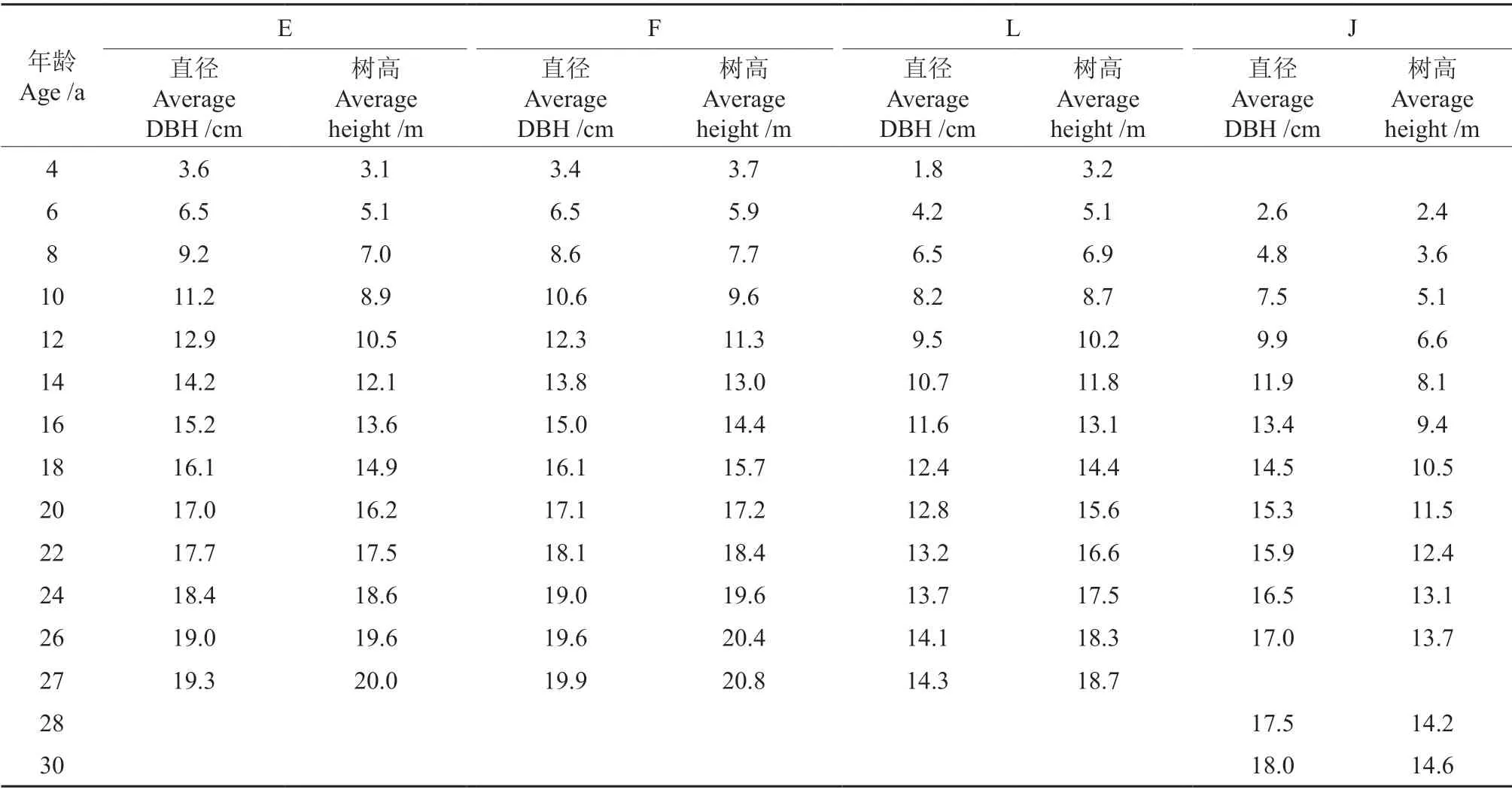
表2 各样地平均解析木的生长过程Table 2 Growth process of Pinus massoniana sample trees

1.2 研究方法

绘制树高与胸径的平方、树高与林分断面积关系的散点图，根据其变化特征构建相关模型，使用决定系数R2、预估精度P值、均方根误差RMSE 以及相对均方根误差RRMSE 这4 项评价指标对模型拟合结果进行评价，表达式如下：

计算林分断面积、林分平均高和林分平均直径的生长率，计算公式如下：

式（5）中：t为调查时的树木年龄；n为间隔期的年数；yt为t年时的某测树因子生长总量；y(t-n)为n年前的生长总量；P(t)为某测树因子在年龄t时的连年生长率，连年生长量用n年的定期平均生长量代替。

分别从林分生长和单木生长两个角度，结合模型中相关因子的变化特点，提出在郁闭林分中存在两个极值的推论，探讨在极值条件下林分自稀疏的方向、强度及轨迹变化，推导出自稀疏率的表达式，预测林分自稀疏的轨迹，分析其规律性。

2 结果与分析

2.1 林分断面积与树高的相关关系

2.1.1 平均木断面积与树高的关系

如图1 所示，在林分郁闭前后，数据材料1各样地的g-H和D2-H都呈直线相关，二者是等价的，前者的直线相关本质上是由后者的直线相关性决定的，因此拟合D2-H相关模型，其表达式为：

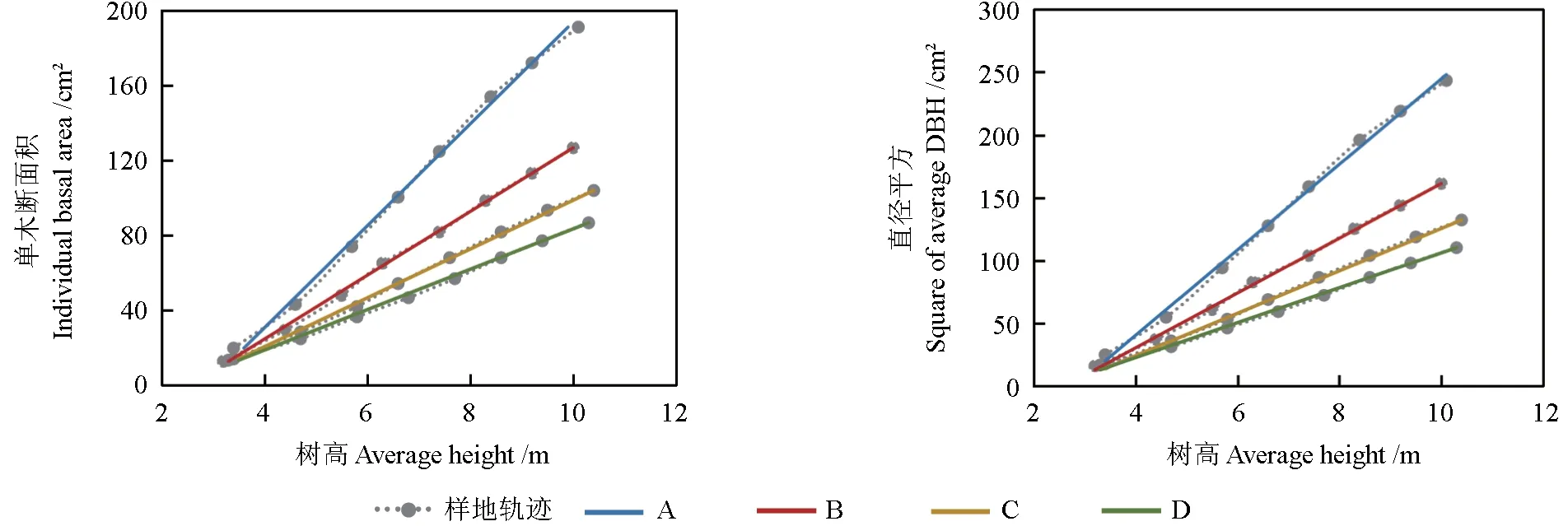
图1 材料1 各样地的单木断面积、直径的平方与树高的关系Fig. 1 Relationship between Individual tree basal area, square of average DBH and average height in various plots of material 1

模型（6）的拟合结果见表3，所有样地的R2都在0.99 以上，P值在0.973 ～0.991 之间，RRMSE 在1.657%～4.916%之间，这些指标很好地说明了在郁闭林分中直径平方与树高近于直线的相关关系。

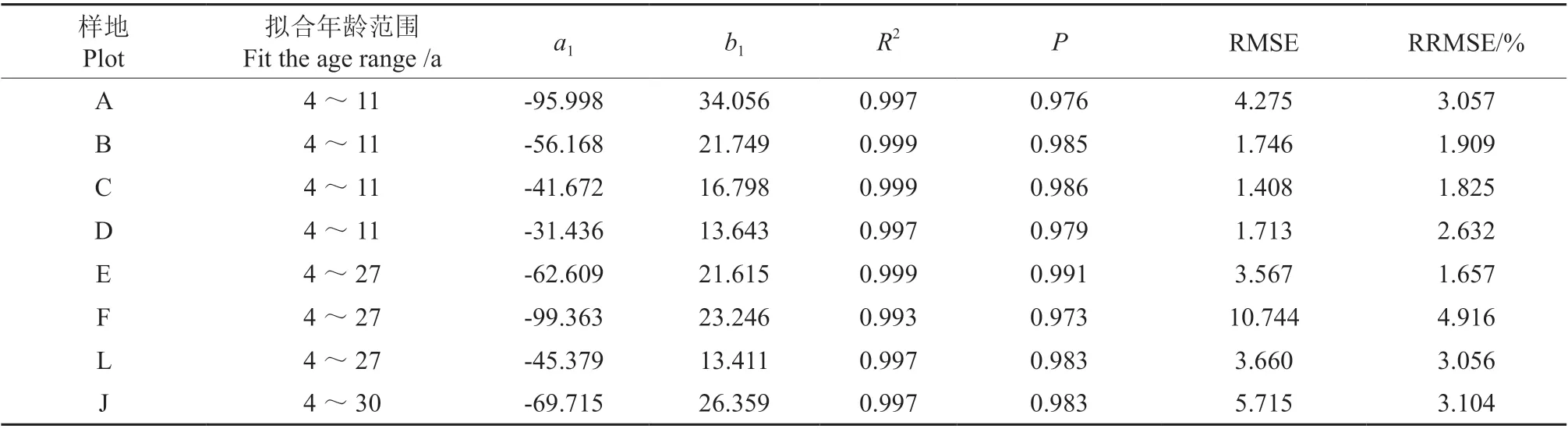
表3 直径平方和树高的模型拟合结果Table 3 Model fitting results of squares of average DBH and average height

2.1.2 林分断面积与树高的相关关系

由于林分总断面积为G=gN，因此在林分株数不变或变化很小的情况下，式（7）成立：

式（7）中：G为林分断面积；a2为截距；b2为斜率。

图2 为材料1 各样地林分断面积与平均树高的相关关系。从图2 可看出，各林分从开始郁闭至自稀疏开始期间，林分断面积与林分平均高呈直线相关关系，满足式（7），其斜率b的大小随林分密度而有规律地变化。模型（7）拟合结果如表4 所示，各项评价指标足以说明从林分初始郁闭至林分自稀疏开始，林分断面积与树高的生长近于直线相关关系。材料1 各样地的斜率b大小顺序为D ＞C ＞B ＞A，造林密度与模型斜率成正比。

以护理学基础教学大纲为依据，通过与教学及临床护理专家研讨，确定临床工作亟须知识及技能，结合贴近临床护理一线工作的理论与实际操作内容，确定教学重点、难点，确定微课作品主题。发放调查问卷，了解对照组护生在护理学基础学习过程中存在的问题及需要加强的知识点，结合护生感性需求，从内容选择、教学活动安排、教学反思等方面设计、制作20节微课，并上传至微信公众平台和校园网络教学平台，供试验组护生观看、学习。

表4 林分断面积和树高的模型拟合结果Table 4 Model fitting results of stand basal area and average height

图2 材料1 各样地的林分断面积与树高的关系Fig. 2 Relationship between stand basal area and average height in various plots of material 1

2.2 对郁闭林分中两个极值点的分析推理

2.2.1 第一个极值点：G/H比值

即在直线生长阶段，林分断面积与树高的生长满足式（8），样地A、B、C、D各年龄段断面积与树高生长率变化如表5 所示。从表5 中可看出，林分郁闭至自稀疏开始的生长阶段，两个因子的生长率基本满足式（8）。

表5 林分断面积与树高随年龄的变化值Table 5 The variation of stand basal area and average height with age

由于式（8）中的a为负值，则有G′/G＞G′/(G-a) ⇒G′/G＞H′/H，即在直线生长阶段断面积生长率PG大于树高生长率PH，图3 清楚地表明了这一点。

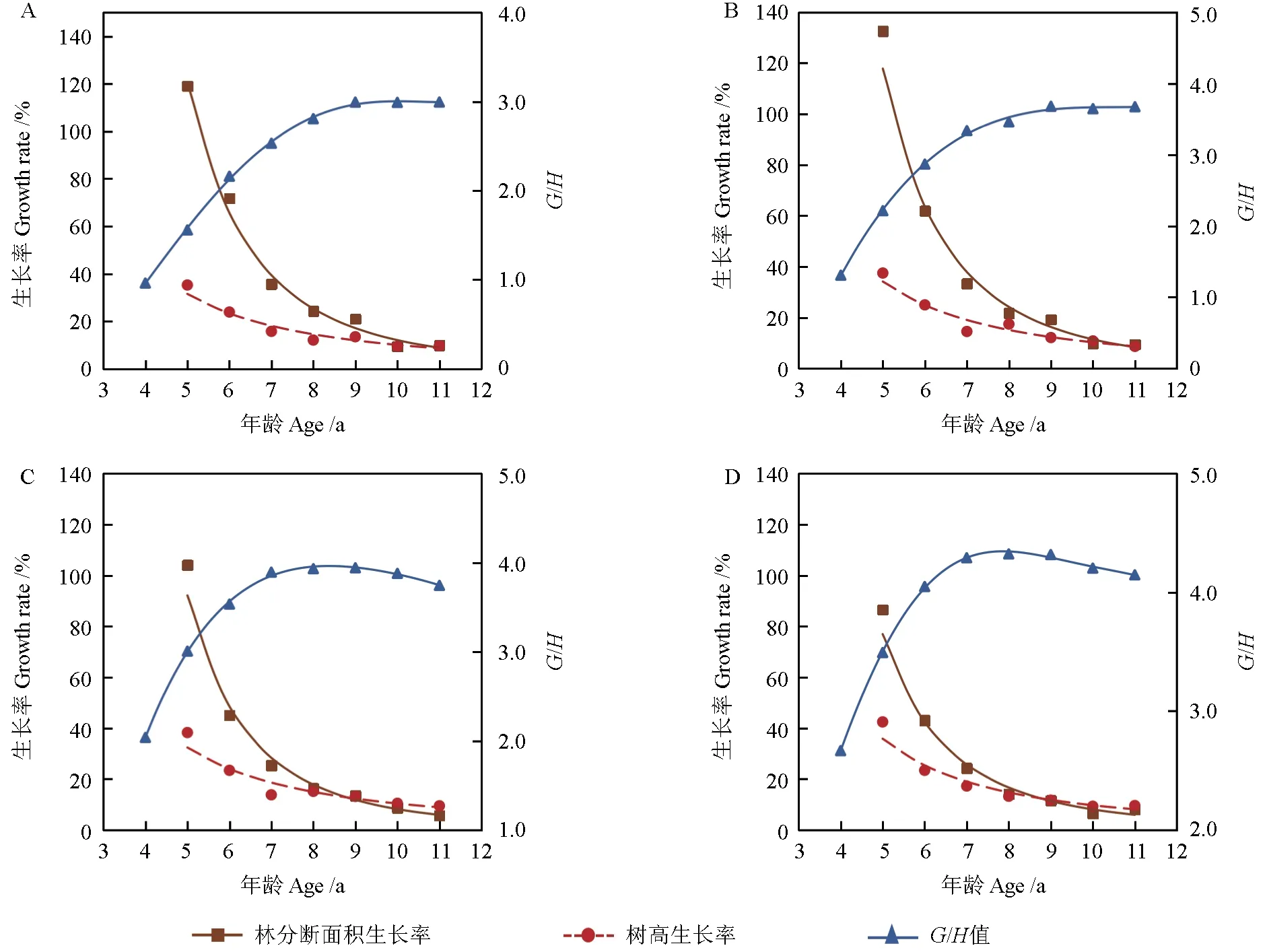
图3 材料1 各样地的生长率、G/H 值与年龄的关系Fig. 3 The relationship between the growth rate, G/H value and age in various plots of material 1

式（9）中：G′为林分断面积连年生长量；H′为平均树高连年生长量。

再从另一个角度分析，将式（7）变形为G/H=b+a/H，对G/H求导有(G/H)′=-(a/H2)，由于截距a＜0，因此(G/H)′＞0，这表明郁闭林分在直线生长阶段其G/H值一直是增大的，其根本原因是林分断面积的生长率PG大于树高生长率PH，且a的绝对值越大，林分的G/H值增加越快。

由此可以推理假设郁闭林分的G/H值不可能无限增加，必定存在一个极限值点(G/H)′=0。G/H值达到极值后便不再增加。因此可设(G/H)′=(HG′-GH′)/H2=0，得到G′/G=H′/H，由极值假设推导出的结果与式（9）完全一致，因此基本可以断定，郁闭林分生长至一定阶段时，林分会达到极值点G/H，此时PG＝PH。

由于自稀疏时林分是充分郁闭的，可以认为林木是一种在极限条件下的生存状态，自稀疏过程就是林木在极限条件下的生长过程，因此自稀疏后林分的生长满足式（9），即PG=PH。从图3可以明显看出，样地A、B、C、D 的林分断面积生长率PG、树高生长率PH以及G/H比值的生长变化完全符合上述分析。即林分郁闭后林分断面积生长率大于树高生长率，在林分达到自稀疏后二者相等；林分的G/H值在自稀疏后不再增加，样地C、D 的G/H值还有所下降，这种情形在后续分析中将作进一步的讨论。

从材料2 各样地直径和树高的生长过程可以看出，林分自郁闭后，因直径的横向生长受阻，树干向上生长争夺生长空间，促进了树高的生长，其各年龄段的树高生长率PH都大于直径生长率PD（图4 和表6），其结果是H/D比值不断增加。由此可以推理假设由于受树木的生物学特性所限，H/D不可能无限增长，也必定存在一个极限值，但在充分郁闭条件下，H/D比值可以保持极值状态的生长，由此得到：(H/D)′=0 ⇒(DH′-HD′)/D2=0 ⇒D′/D=H′/H，即H/D达到极值后，树高生长率等于直径生长率，即通常所说的同速生长阶段。

图4 中，PH与PD相交的点有2 个：1 个是林分郁闭后，树高生长率由小于直径生长率向大于直径生长率变化，但这个点不是极值点，因为在此后树高的生长率大于直径生长率；第2 个极值点是由树木的生物学特性所决定的，极值点之后其H/D值不会再增大，林木的树高与直径保持同速生长。

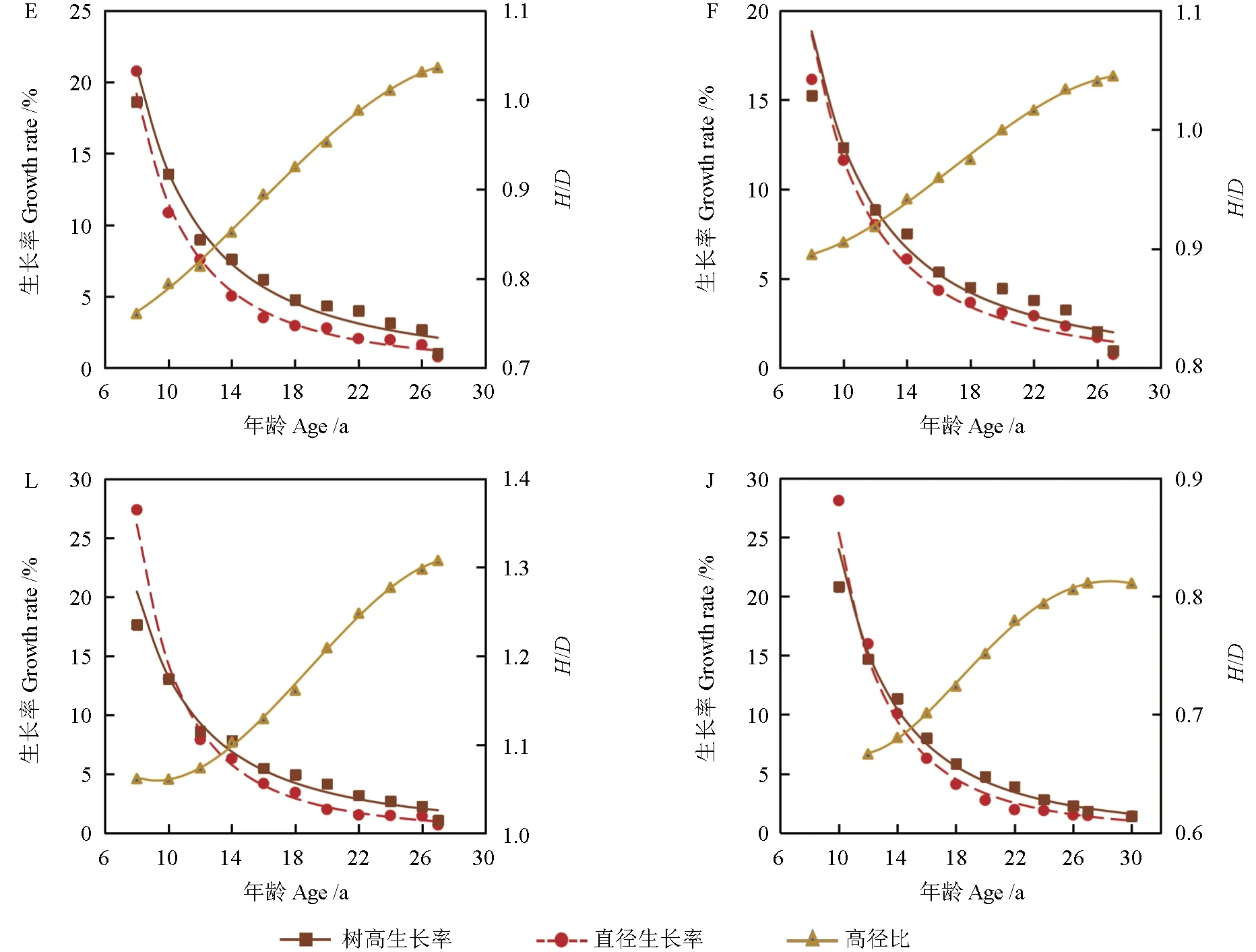
图4 材料2 各样地的生长率、H/D 与年龄的关系Fig. 4 The relationship between growth rate, H/D and age in various plots of material 2

图4 和表6 都表明，样地E、F、L、J 林分郁闭后其树高生长率均大于直径生长率，林分的H/D值增长迅速，但至后期已相对缓慢，从变化趋势分析已经接近或达到其极值点了，如样地E、F、J的PD与PH已经完全相等，表明这3 个样地的林分已经达到第2 个极值点。

表6 直径与树高随年龄的变化值Table 6 The variation of average DBH and average height with age

2.3 林分自稀疏轨迹及自稀疏率

林分开始自稀疏后，因为试验目的或经营习惯的原因，一些林分中的枯立木可能会被及时清除，此时林分的生长空间得到释放，竞争有所减弱。但有些林分其枯立木可能不会被及时清除，林分内仍然较拥挤，影响保留木的生长。而在一般的试验或生产中，对枯立木是不做清除的。

对于这两种不同处理方式的林分，其自稀疏的轨迹和林分的自稀疏率会存在差异，下面对这两种情形分别作如下分析。

2.3.1 及时清除枯立木的自稀疏线

由前面分析可知，林分的自稀疏线满足式（9），此时林分断面积生长量为G′=(GH′)/H=GPH，而不发生稀疏的林分断面积的生长量为GPG=2GPD，得到林分的断面积枯损量为二者之差：

由图5 可看出，所推导的自稀疏线与实际稀疏线方向基本一致，其特点是单位树高生长量所产生的断面积生长量相等。

图5 材料1 各样地的自稀疏线Fig. 5 The self-thinning line in various plots of material 1

2.3.2 不清除枯立木的自稀疏线

不清除枯立木，同时枯立木也没有脱落、分解，仍然占据原生长空间，或部分脱落和分解，则活立木的生长会受影响，其总生长量会逐年减少。设清除枯立木时，断面积年生长量为ZG1=GPH，枯损的断面积为βG，假设还有K的枯立木保持在林分中没脱落，这部分林木还占据生长空间，由此引起断面积生长量减少的值为βGK，则林分实际断面积生长量为：

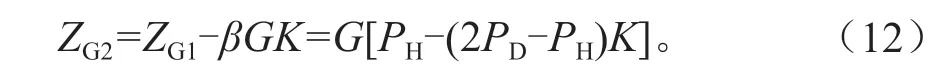
图6 是假设枯立木仍有K=15%保持在林分中的自稀疏状态预测，从自稀疏趋势分析，其拟合的曲线与实际自稀疏线吻合更好，说明试验林分的自稀疏是在这种状态下开始的，即林分中的枯立木没有被清除，影响了保留木的生长，其结果是单位树高生长量所产生的断面积生长量逐年下降。这应该是图3 中C、D 样地其G/H值下降的原因。

图6 材料1 各样地的自稀疏线Fig. 6 The self-thinning line in various plots of material 1

3 讨论

林分极值点1 即G/H值仍然难以精确确定，因为它不是一个固定值，而是因初始密度而变化的，因此准确确定林分自稀疏的起始年龄仍比较困难。第2 个极值点即H/D的值可以较准确预测，此时树高生长率与直径生长率相等。对于密度较大的林分，第1 个极值点会早于第2 个极值点到达，如果降低林分密度可以推迟第1 个极值点到达的时间。由此可以推断，林分可能存在某一条密度线，使两个极值点同时到达。从人工林经营角度分析，使两个极值同时达到的林分密度可以称为合适的或适宜的林分密度，因为达到极值的时间较晚，树高已充分生长，H/D比值大，树干圆满通直，林木单株材积和林分的蓄积量都较大；如果林分密度过大，虽然在短期内林分的平均断面积和平均蓄积量较高，但由于树高、直径均较小，其径级小，出材率低，价值也较低，且由于自稀疏早，经营周期缩短，增加了整地、造林和培育的成本和风险。

从数据和图形分析可知，不同初始密度林分的自稀疏线不会重合，因为自稀疏的起始年龄不同，此后林分的树高、直径及它们的生长率也不同，其轨迹不会重合。据此分析每个林分都应该有其各自的自稀疏线。郁闭林分的两个极值在其他树种的纯林中也应该是存在的，只是因为树种特性的差异，其直线生长模型的参数值以及G/H和H/D的比值会不同。

本研究提出的两个极值点的推论合理解释了众多学者研究自稀疏方程时得出斜率有差异的原因，这是因为在极值点H/D到来之前，PH不等于PD，树高和直径为异速生长，在极值点H/D达到之后两者才为同速生长；也解释了同一树种不同年龄阶段的林分或同一林分的不同生长阶段，林分枯损率不同的原因，因为林木的自稀疏率是由树高和直径的相对生长关系所决定的，在不同的自稀疏阶段，其相对生长关系不尽不同。由此也可以分析得到，在林分生长的某个阶段进行抚育间伐，可以促进直径生长率的提高，直至达到第一个极值点开始稀疏，这就是间伐抚育效应。

马尾松是一种常绿针叶树种，叶有蜡质层，较难分解，常有部分枯立木保留在林分中的情况，这是保留的活立木生长量减小的主要原因。但不清除枯立木的情形比较复杂，因树种、气候不同，枯立木脱落分解的速率也会不同。因此对于这种状态的林分，准确预测其自稀疏线仍比较困难。

对于自稀疏规律的争论之一是，自稀疏线是直线还是曲线，一些研究表明自稀疏线是曲线，因为自稀疏线的实际斜率随着年龄和树的大小的增加而变陡[4]。在本研究中，分析得出当及时清除枯立木时，自稀疏线是直线，而不及时清除枯立木，则自稀疏线为曲线。后一种情况在实际中更为普遍，本文研究所用试验样地中的枯立木是没有被清除的，显然属于后一种情形。

文中所提出的两个极值及自稀疏规律，都是在林分保持充分郁闭情况下发生的现象，而对于老年林分，因其生长势衰，需要更多的阳光，由此而引起树冠和枝叶减少，郁闭度下降，其规律就更复杂，本文中对此没有涉及。但从林分年龄分析，样地A、B、C、D 都属于幼龄林，还未进入衰老阶段，因此其自稀疏的发生应该是由密度引起的，这与何斌等人[28]的分析一致。

本文中分析得出郁闭的马尾松林分在自稀疏之前其G-H呈直线相关，笔者在对杉木人工林的研究中也得到类似结论，其详情将后续介绍。由于连续监测的密度试验林材料较少，极值理论目前仅在马尾松、杉木人工林中得到论证，至于其他树种有无类似关系有待论证。今后将集中在模型参数的生物学意义、不同密度林分开始自稀疏的准确时间、不同密度林木生长的相互关系以及抚育间伐效果分析等关键理论问题上开展研究。