半群作用的共轭性*

羌湘琦， 侯成军

(扬州大学数学科学学院， 225002，江苏省扬州市)

0 引 言

算子代数与遍历理论之间的联系始于von Nuemann代数的群测度空间构造[1]. 至今为止，有关可数无限群在概率测度空间上的自由遍历保测作用在“共轭”“轨道等价”和“W*-等价”等意义下的分类与群测度空间构造的有限因子理论的研究取得了丰富成果[2]. 平行于自由遍历的保测作用，群在拓扑空间上的同胚作用与相应交叉积C*-代数理论的研究早期最著名的结果是由Giordano,Putnam和Skau[3]于1995年给出的，他们证明了Cantor集上的两个极小同胚是强轨道等价的当且仅当对应的交叉积C*-代数是同构的. 1998年，此结果被Boyle和Tomiyama[4]推广，证明了紧度量空间上两个拓扑自由的同胚是flip共轭的当且仅当交叉积C*-代数之间存在保典则函数子代数的*-同构. 后来，Lin和Matui[5]定义了Cantor极小系统的弱逼近共轭，逼近K-共轭等，通过K-理论研究了这类系统的分类与相应的交叉积C*-代数之间的关系. 最近，Li[6]引入群同胚作用的连续轨道等价概念并借助于相应交叉积C*-代数的同构性质对该理论进行了刻画. 此外，众多学者也对Smale空间，双边Markov移位等同胚提出了渐近连续轨道等价，flow等价等概念，并用相关的Ruelle代数，Cuntz-Krieger代数和广群C*-代数进行了刻画，得到了丰富且重要的结论. 相关研究成果可参见文献[7-9].

2010年Matsumoto[10]引入单边拓扑Markov移位的连续轨道等价概念，并建立了此与Cuntz-Krieger代数之间的联系. Carlsen[11]等人又利用广群技巧将Matsumoto和Matui[8]对不可约单边拓扑Markov移位的轨道等价的研究推广到单边有限型移位上. 注意到单边移位是紧度量空间上的局部同胚. 受上述研究的启发，本文借助于变换广群性质和Ruelle算子理论研究半群作用的共轭性.

1 预备知识

本文中所涉及的半广群、广群及其C*-代数的相关定义参见文献[12-15]. 对于半广群Λ，用Λ(2)表示Λ的可乘元素对集. 给定半广群Λ和Γ，映射Ψ：Λ→Γ被称为半广群同态，如果对(a,b)∈Λ(2)，有(Ψ(a)，Ψ(b))∈Γ(2)且Ψ(ab)=Ψ(a)Ψ(b). 进一步，如果Ψ是双射且Ψ-1也是半广群同态，则称Ψ是半广群同构. 注意到任意的半群都可以自然地看做是半广群. 对于拓扑广群G，我们用G(2)和G(0)分别表示G的可乘元素对集和单位空间. 令x∈G，分别称d(x)=x-1x和r(x)=xx-1为x的domain和range. 如果d和r是局部同胚，则称广群G是étale的. 若集合{u∈G(0):d-1(u)∩r-1(u)={u}}是G(0)的稠子集，则称G是拓扑一致(principle)的. 给定étale广群G和H，称映射Φ：G→H是同态，如果Φ是连续的且对(r,r′)∈G(2)时有(Φ(r)，Φ(r′))∈H(2)，Φ(rr′)=Φ(r)Φ(r′). 进一步，若Φ是同胚使得Φ和Φ-1是同态，则称Φ是étale广群同构. 从广群G到群G的同态被称为G上的(连续)cocycle.

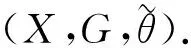
例1.1[11]令0是非负整数加法半群，A是有限集，A表示从0到A的映射全体.在A上赋予离散拓扑，A上赋予相关的乘积拓扑，则A是一个紧的极端不连通空间.A上的移位变换σ：A→A定义为σ(x)(i)=x(i+1)，∀x∈A，i∈0. 令X是A的闭子集且在σ下不变，即σ(X)=X，此时X是A的紧子集且被称为单边移位空间. 用σX表示σ对X的限制，σX是局部同胚当且仅当X是有限型移位，此时对也是局部同胚，故当X是有限型单边移位时可得半群作用(X，0，σX).

(x，m)(y，n)=(x，mn)，若y=θm(x).

另一个是变换广群

G(X，P，θ)={(x，g，y)∈X×G×X:∃m，n∈P，g=mn-1，θm(x)=θn(y)}，

其上的乘法和逆运算分别为

(x，g，y)(u，h，v)=(x，gh，v)，若y=u，(x，g，y)-1=(y，g-1，x)，

(2) 映射cθ:G(X，P，θ)→G定义为cθ(x，g，y)=g是(连续)cocycle；

下面给出半群作用共轭的概念.

定义1.3设(X，P，θ)和(Y，S，ρ)是两个半群作用. 如果存在同胚φ：X→Y，半群同构α：P→S，使得对∀m∈P,φθm=ρα(m)φ，则称(X，P，θ)和(Y，S，ρ)是(拓扑)共轭的，称二元组(φ，α)是(X，P，θ)到(Y，S，ρ)的共轭，简称为共轭.

定义1.4 设(X，P，θ)是半群作用. 如果对m，n∈P且m≠n，集合{x∈X：θm(x)=θn(x)}的内部是空的，则称(X，P，θ)是本质自由的.

定义1.5[11]设X和Y是两个有限型单边移位. 如果存在同胚φ：X→Y使得φ∘σX=σY∘φ，则称σX和σY共轭.

定义1.6[6]设(X，G，α)和(Y，H，β)是两个群作用，如果存在同胚φ：X→Y，群同构γ：G→H，使得对∀g∈G,φαg=βγ(g)φ，则称(X，G，α)和(Y，H，β)是共轭的.

引理1.7[16]半群作用(X，P，θ)是本质自由的当且仅当广群G(X，P，θ)是拓扑一致的.

推论1.10设(X，P，θ)和(Y，S，ρ) 是两个本质自由的半群同胚作用，P⊂G，S⊂H满足本节第二段中假设，则以下陈述等价：

(1) étale广群G(X，P，θ)同构于G(Y，S，ρ)；

2 主要结论

命题2.1 两个有限型单边移位σX和σY是共轭的当且仅当对应的半群作用(X，0，σX)和(Y，0，σY)是共轭的.

证明必要性. 设同胚φ：X→Y引起了σX和σY的共轭. 令α：0→0是恒等映射，则对∀x∈X,m∈0,有

因此(X，0，σX)和(Y，0，σY)是共轭的.

充分性. 设(φ，α)是(X，0，σX)到(Y，0，σY)的共轭，则α是0上的恒等映射，并且因此有限型单边移位σX和σY是共轭的. 证毕.

设(X,P,θ)是半群作用,C(X)表示X上连续函数全体，定义

命题2.3 设(X，P，θ)和(Y，S，ρ)是两个半群作用，φ：X→Y是同胚，α：P→S是半群同构，定义Λ：C(X)→C(Y)，f|→f∘φ-1,则Λ是*-同构，并且下列陈述等价:

(1) (φ，α)是共轭；

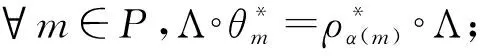
(3) ∀m∈P，Λ∘(θm)*=(ρα(m))*∘Λ.

证明容易验证Λ：f|→f∘φ-1是C(X)到C(Y)上的*-同构，下证(1)⟺(2)⟺(3).

(1)⟹(2).对∀f∈C(X)，y∈Y，有

(2)⟹(1). 对∀f∈C(X)，y∈Y，有

因此，θm(φ-1(y))=φ-1(ρα(m)((y))，i.e.，对∀x∈X，m∈P，φ(θm(x))=ρα(m)(φ(x)).

(3)⟹(1). 由于对∀f∈C(X)，Λ((θm)*(f))=(ρα(m))*(Λ(f))，因此

(1)

Ψ(x，m)Ψ(θm(x)，n)=(φ(x)，α(m))(φ(θm(x))，α(n))=(φ(x)，α(mn))=Ψ(x，mn).

证明本证明参考文献[6]有关连续轨道等价的证明. 事实上，如果令(φ，α)是(X，P，θ)到(Y，S，ρ)的共轭，映射(x，mn-1，y)∈G(X，P，θ)→(φ(x)，α(m)α(n)-1，φ(y))∈G(Y，S，ρ)实现了上述的étale广群同构，再结合引理1.7，1.9即可.

证明必要性由定理2.5及其证明可得. 下证充分性.

φ(θm(x))=ρa(x，m，θm(x))(φ(x))，

(2)

φ-1(ρt(u))=θb(u，t，ρt(u))(φ-1(u)).

(3)

a(x，m，θm(x))=a(y，m，θm(y)).

(4)

同样的，对∀u，v∈Y，t∈S，有

b(u，t，ρt(u))=b(v，t，ρt(v)).

(5)

由式(2),式(3)可得对∀x∈X，m∈P，θb(φ(x)，a(x，m，θm(x))，ρa(x，m，θm(x))(φ(x)))(x)=θm(x).再由式(4),式(5)可得对∀x′∈X，θb(φ(x)，a(x，m，θm(x))，ρa(x，m，θm(x))(φ(x)))(x′)=θm(x′).(X，P，θ)的本质自由性表明

b(φ(x)，a(x，m，θm(x))，ρa(x，m，θm(x))(φ(x)))=m.

(6)

同样的，对u∈Y，t∈S，有

a(φ-1(u)，b(u，t，ρt(u))，θb(u，t，ρt(u))(φ-1(u)))=t.

(7)

定义α：m∈P→a(x，m，θm(x))∈S，β：t∈S→b(u，t，ρt(u))∈P，则由式(4)～式(7)，α是从P到S上以β为逆的半群同构. 再由式(2),φ(θm(x))=ρα(m)(φ(x))，因此(X，P，θ)和(Y，S，ρ)共轭.

定理2.7设(X，P，θ)和(Y，S，ρ)是两个同胚半群作用，P⊂G，S⊂H满足第一节中假设，则下列陈述等价:

(1) (X，P，θ)和(Y，S，ρ)共轭;

证明(1)⟹(2) 设(φ，α)是(X，P，θ)到(Y，S，ρ)的共轭. 对∀g∈G，存在m，n∈P使得g=mn-1. 定义β：G→H，g|→α(m)α(n)-1，若g=ab-1=mn-1,a，b，m，n∈P. 取p，q∈P使得ab-1=mn-1=p-1q，则pa=qb，pm=qn，并且α(p)α(a)=α(q)α(b)，α(p)α(m)=α(q)α(n)，因此α(a)α(b)-1=α(p)-1α(q)=α(m)α(n)-1，从而β是良定义的. 由α是双射容易验证β也是双射.

下证同态性. 给定g，h∈G，令g=ab-1，h=cd-1，其中a，b，c，d∈P. 取m，n∈P使得b-1c=mn-1，则α(b)-1α(c)=α(m)α(n)-1.因此

β(gh)=β(ab-1cd-1)=β(am(dn)-1)=α(am)α(dn)-1=α(a)α(m)α(n)-1α(d)-1=

α(a)α(b)-1α(c)α(d)-1=β(g)β(h)，

从而β：G→H是群同构. 进一步，对∀m∈P，β(m)=α(m)α(e)-1=α(m)，所以β(P)=S.对x∈X，g=ab-1∈G，其中a，b∈P，由注解2.2，