一类非线性分数阶微分方程正解的存在性*
2022-07-19张克梅
陈 艳, 张克梅
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
最近几十年来,分数阶微分方程已经被应用于各种领域,各国的学者把他们的研究方向转向分数阶微分方程,具体可参考文献 [1-3]. 近年来,有关分数阶微分方程边值问题的研究已经取得了很多成果,具体可参考文献[4-7].
带有奇异项的分数阶微分方程边值问题的研究是分数阶微分方程的一个重要领域.
文献[8]研究了边值问题
(1)

文献[9]研究了下列带有多点边界条件的微分方程边值问题
(2)
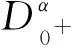
文献[10]研究了带有积分边界条件的微分方程边值问题
(3)
其中Dδ和Dτ是标准的Riemann-Liouville分数导数,1<δ≤2,0<τ<δ,f,g:[0,1]×[0,1]→[0,+∞)是给定的连续函数,对任意t∈[0,1],g(t,x)关于x是非负的,并且f不需要任何单调性假设. 其作者将Schauder不动点定理和上下解方法相结合得到了边值问题(3)正解的存在性,用Banach压缩映射原理得到了该问题解的唯一性.
受上述文献的启发,本文研究了下列带有积分边界条件的两项分数阶微分方程
(4)
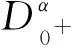
本文的创新之处在于:与文献[11]相比,本文加入了积分边界条件; 与文献[12-14]相比,本文研究的分数阶微分方程包含两个项; 与文献[10] 相比,本文研究的非线性项可以是奇异的.
全文安排如下:第1部分介绍了一些后续证明用到的定义定理; 第2部分用锥上的不动点定理证明了边值问题方程(4)正解的存在性; 第3部分介绍了一个例子验证所得结果.
1 性质和引理
该部分介绍了一些分数阶理论的定义,并给出了一些相关引理.
定义1.1[15]设f:(0,+∞)→是可测函数,则f的α(α>0)阶Riemann-Liouville分数积分定义为
这里Γ是Euler-Gamma函数,等号右边在(0,+∞)是逐点定义的.
定义1.2[15]设f:(0,+∞)→是可测函数,则f的α(α>0)阶Riemann-Liouville分数导数定义为
等号右边在(0,+∞)是逐点定义的, 这里n=[α]+1,其中[α]是实数α的整数部分.
定义1.3[15]一个双参数的Mittag-Leffler函数Eα,β(x)定义为

当β=1时,Eα,1是通常的Mittag-Leffler函数Eα.
定理1.4[15]令n-1≤α≤n(n∈),λ∈,h是(0,+∞)上的实函数, 则方程
-Dαu(t)+au(t)=h(t),t>0,
是可解的,其通解可由下列式子表示
其中cj∈,j=1,…,n.
为了方便,介绍以下符号
g(t)=tα-1Eα,α(atα),
(5)

本文从始至终要求以下3个条件成立:
(H1)a∈(0,a*]是一个常数;
(H3)f(t,0)≢0,t∈[0,1].
引理1.5令h∈L1[0,1]∩C(0,1),假设(H2)成立,则线性两项分数阶边值问题
(6)

证明由定理1.4和(5)式,问题(6)的解可以表示成

由边界条件u(0)=u′(0)=0,得c3=c2=0.因此

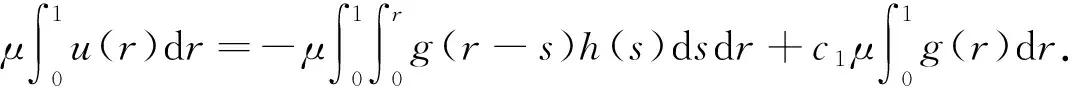

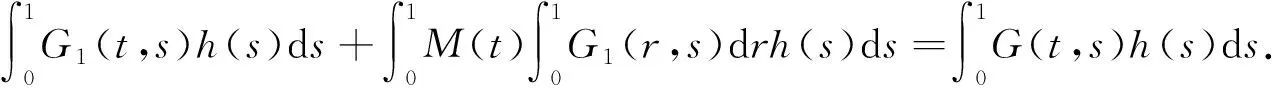
引理1.6[11]假设(H1)成立,s*∈(0,1)满足s*=(1-s*)α-2,则G1(t,s)满足:
(P1)G1(t,s)>0,∀t,s∈(0,1);
(P2)G1(t,s)=G1(1-s,1-t),∀t,s∈[0,1];


证明由引理1.5和引理1.6得


ρ2[1+M(t)]s(1-s)α-1≤ρ2[1+M(1)]s(1-s)α-1=W2s(1-s)α-1.
设J=[0,1],从J到n的所有连续泛函组成的空间E=C(J,n)是Banach空间.任意u(t)∈n,定义范数令P={u∈E:u(t)≥0,t∈[0,1]}是E中的一个锥.建立P的一个子锥对任意R>0,令
定义一个线性算子L:E→E如下

(7)
引理1.8[16]设L:E→E是一个连续线性算子,P是一个全锥,且L(P)⊂P.如果存在ψ∈E(-P)和一个常数c使得cL(ψ)≥ψ,则L的谱半径r(L)≠0并且有一个属于它的第一特征值λ=r(L)-1的特征函数.
引理1.9(7)式定义的算子L:P→K是一个全连续线性算子,并且谱半径r(L)≠0,L有一个属于它的第一特征值λ=r(L)-1的正的特征函数φ*.
证明对任意u∈K,由引理1.7得
所以L:K→K.由G(t,s)在t,s∈[0,1]×[0,1]一致连续,得L:K→K是全连续线性算子.
接下来,用引理1.8证明L的第一特征值λ>0.
事实上,对任意t∈[0,1],选取u(t)=tα-1.显然u∈K,则有


根据引理1.8,谱半径r(L)≠0,并且L有一个属于它的第一特征值λ=r(L)-1的特征函数φ*使得λLφ*=φ*.
为了处理奇异性,采取如下假设:
(H4)f∈C((0,1)×(0,+∞),[0,+∞))对任意0 (ⅰ) 任意u∈∂KR,‖Au‖≤‖u‖; (ⅱ) 任意u∈∂Kr,σ>0,存在u0∈K{θ},使得u≠Au+σu0成立; 比较上述式子,得 (8) 因此,由延拓定理得T:K{θ}→P是良定义的. 成立. 由勒贝格控制收敛定理得:当n→∞时, 另外,当n>N时, 下一步,证明T(D)等度连续. 事实上,由(H4)得,任意>0,存在自然数k使得 这说明T(D)等度连续. 定理2.2假设条件(H1),(H2),(H3),(H4)成立,并且 (9) 其中λ1是L的第一特征值, 则边值问题(4)至少有一个正解. 证明首先证明任意u∈∂KR,有‖Tu‖≤‖u‖.事实上,任意u∈∂KR,由引理1.7得 接下来,验证引理1.10(ⅱ)成立. 由(9)式得,任意t∈[0,1],存在r1>0,当0 设φ*是L的属于λ1的正特征函数,则φ*=λ1Lφ*.假设T在∂Kr1上没有不动点(否则证明结束). 考虑微分方程边值问题 (10) 所以(H2)成立. 另外(H3)显然成立. 根据定理2.2,问题(10)至少有一个正解.



2 主要结果
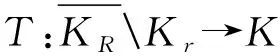










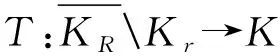


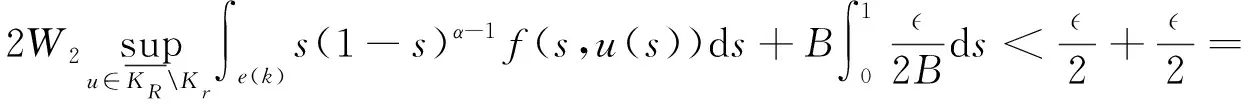





3 例 子