磁振子宏观效应以及热扰动场对反磁化的影响*

李柱柏 魏磊 张震 段东伟 赵倩

1) (内蒙古科技大学材料与冶金学院,包头 014010)

2) (内蒙古科技大学理学院,包头 014010)

热扰动导致的磁反转是越过能量势垒的不可逆反转,称为热助隧穿.本文研究Pr-Fe-B 磁体热扰动导致的磁反转弛豫现象,反转磁矩与时间自然对数关系可表示为与能垒之间的关系,因此反磁化弛豫现象可用磁振子按能量的玻色统计分布率来解释,是磁振子宏观效应的体现.反磁化不可逆过程的临界尺寸为纳米级,与理论磁畴壁尺寸接近,证实热扰动反磁化经过磁畴壁形核去钉扎过程.在实空间反磁化耦合体积增大能减小磁振子隧穿的反磁化概率,热扰动场减小;热扰动后效场测量值与热扰动场计算值基本是一致的.温度升高,热扰动能量增大,由于耦合作用热扰动后效场有所减小,但热扰动后效场相对于矫顽力的作用增大.

1 引言

磁体反磁化是微观磁矩反转的宏观体现,除了外磁场,热扰动也会推动磁体反磁化[1,2],即热助隧穿[3].对于磁有序系统,磁矩和自旋矢量热运动称为热扰动.因为交换作用,磁矩热扰动会带动临近磁矩进动,在温度不太高的情况下,热扰动可以理解为一系列自旋波组合[4].这和晶格格点振动产生的格波(声子)类似,因此自旋波也称为磁振子.尽管对反磁化过程有较多研究,但从微观准粒子磁振子角度对反磁化过程探讨很少,而且反磁化形核、钉扎、非一致反转等过程一直是难以理清的概念[5,6].为降低磁反转需要的能量,反磁化过程一般需要经过反磁化畴形核[7,8].对于具有高矫顽力的永磁体,反磁化形核发生在磁晶各向异性场较低区域.当反磁化形核体积达到临界时,才会突破钉扎发生不可逆位移和拓展[9].临界形核体积大小反映了磁晶各向异性能、交换能和塞曼能之间的竞争和平衡[10,11],因此,推测反磁化临界形核体积是理解反磁化过程的关键.本文对Pr-Fe-B 磁体热激活反磁化进行分析,从磁振子这个微观层面解释不可逆反磁化临界过程,研究临界过程需要越过的体积,进一步深入理解反磁化形核和钉扎过程.而且,磁性能随温度上升而衰减对磁体热稳定性是不利的,热扰动对热稳定性影响程度也是需要探讨的问题[12].

2 实验方法

本实验制备Pr-Fe-B 磁体薄带,并对Pr-Fe-B 薄带进行磁性测试和分析,薄带分子式按原子百分比为Pr13Fe81B6.先按分子式成分将稀土金属Pr,Fe 和Fe-B 合金称重配料,采用电弧熔炼成合金块.将合金小块放入底部有小孔的石英管中,然后感应熔炼成熔液后用氩气吹到旋转铜辊上制成薄带,通过调整铜辊转速使薄带的反磁化曲线方形度和矫顽力最佳.薄带厚度为1—2 mm,X 射线衍射证实薄带主要为Pr2Fe14B 相纳米晶结构.采用QD公司超导量子干涉仪振动磁强计(SQUID VSM)测量薄带磁滞回线、回复曲线、热激活反磁化曲线.磁性测量时所加磁场与薄带长度方向平行,薄带厚度与长度比约为零,因此样品沿长度方向退磁因子几乎为零、可忽略不计.

3 结果与讨论

图1(a)为薄带在温度300 K 测得的磁滞回线,矫顽力为19.4 kOe (1 Oe=103/(4π) A/m).快淬薄带结构各向同性,但反磁化曲线具有较好方形度,说明薄带结构均匀,晶粒之间有较好耦合作用,反磁化行为较为一致.为研究热扰动对反磁化的影响,将磁体正向磁化饱和,然后分别加反向场15,18,20 kOe 并保持1200 s.如图1(b)所示,在反磁化场保持不变的情况下,磁矩仍然会反转,但反磁化磁矩随时间增加而逐渐减小.由于永磁体内禀磁晶各向异性能,自旋磁矩矢量平行于易磁化轴能量最低,但热运动会使自旋磁矩偏离易轴即平衡位置而扰动,这样因为交换作用会引近邻原子磁矩进动,从而产生自旋波,在物理上也称为磁振子.在外场保持不变情况下,磁矩反转源于磁矩热扰动越过能量势垒不可逆反磁化[13].如图2(a)所示,反转磁矩值与时间的自然对数呈线性关系,满足公式M(t)=Slnt+const,M(t)为与时间t相关磁矩值,S为磁黏滞系数,const 为常数.由于反转磁矩与时间自然对数呈线性关系,时间t可表示为自然指数函数形式,为弛豫时间τ=τ0exp[ΔEi/(kBT)]的倍数.这里τ0为一预设指数因子,ΔEi为能量势垒,kB为玻尔兹曼常数,T为温度.这是按能量势垒ΔEi的玻尔兹曼系统分布ƒ=ƒ0exp[–ΔEi/(kBT)]结果,ƒ0是τ0的倒数,为一预设频率[14].

按照上述分析,M(t)与时间t之间关系就体现为M(t)与能垒ΔEi之间的关系.从图1 可以看出,从反向场17 kOe 到21 kOe 的反磁化曲线斜率是基本一致的,因此能垒ΔEi增大斜率是线性的,在反向场18 kOe 和20 kOe 的M(t)与时间自然对数关系,即M(t)与能垒ΔEi之间是线性关系.在反向场15 kOe,绝大部分晶粒磁矩处于正向,只有极少部分晶粒反磁化,ΔEi变化很小,可以认为ΔEi变化是线性的,所以在15 kOe 反向场的M(t)与时间自然对数也呈线性关系(见图2(a)).在磁有序体系微观上自旋磁矩热运动可理解为磁振子的形式.磁振子为玻色子,按能量分布统计率应符合玻色统计率ff0{exp[∆Ei/(kBT)]−1}−1,在高能态∆Ei/(kBT)≫1,可简化成ff0exp[−∆Ei/(kBT)].根据上述统计分布律,随能量升高磁振子数以指数形式减少.

图1 (a) Pr-Fe-B 磁体薄带在300 K 的磁滞回线(1 emu/g=1 A·m2/kg);(b) 分别施加反向场15,18,20 kOe 并保持1200 s 条件下磁矩的变化Fig.1.(a) Hysteresis loop of Pr-Fe-B magnet at temperature of 300 K;(b) the variations of magnetic moments with the time under the field of–15,–18 and–20 kOe,respectively.

图2 (a) 反转磁矩与时间自然对数关系;(b) 热扰动反磁化后效场Haf 的测量和拟合Fig.2.(a) Dependence of magnetic moments on the natural logarithm of time;(b) the fitting and measurement of the aftereffect of thermal fluctuation.

按照上述理论,即使外场保持不变,由于热运动磁矩也能克服能量势垒反转,降低磁体矫顽力,这是磁振子的宏观效应.在热扰动和外场作用下,磁反转克服的能量势垒为H+ΔEi,外磁场只降低了磁体反磁化势垒H,热扰动克服能量势垒为ΔEi.如预设ƒ0为7.2×1010s–1(τ0=1.39×10–11s),按照公式ττ0exp[∆Ei/(kBT)],弛豫时间τ为1 s,大部分小于25kBT的能量势垒ΔEi能被克服[14].

为验证热扰动反磁化效果,对其后效场Haf进行测量.如图2(b)所示,在反磁化场18 和20 kOe分别保持1200 s,再以速度10 Oe/s 增大磁场,当磁场增大到一定值时,磁矩才会明显下降.对反磁化曲线做切线拟和,反磁化后效场Haf均为0.36 kOe.在反磁化曲线的一般测量过程中,可近似认为每个测量点磁场等待时间很短,约为1 s.基于此测量数据,可计算由于热扰动导致矫顽力降低值.按公式ττ0exp[∆Ei/(kBT)],1 s 对应所克服势垒约为25kBT,1200 s 对应的大致为32.1kBT,其差值为7.1kBT,对应热扰动后效场Haf为0.36 kOe.以此计算,每单位kBT对应矫顽力降低值为0.05 kOe,保持1200 s 大体能克服势垒ΔEi为32.1kBT,矫顽力降低值为1.6 kOe.

可采用扰动场Hf表示热扰动对反磁化的作用.图3(a)为根据热激活反磁化曲线获得的磁黏滞系数S和由回复曲线获得的不可逆磁化率xirr,图3(b)为由公式Hf=S/xirr计算得到的热扰动场[15].如图3(b)所示,Hf在0.04—0.1 kOe 之间,这和根据统计分布率获得热扰动能量kBT对应矫顽力降低值0.05 kOe 接近,说明Hf计算值与热扰动宏观效应基本符合.

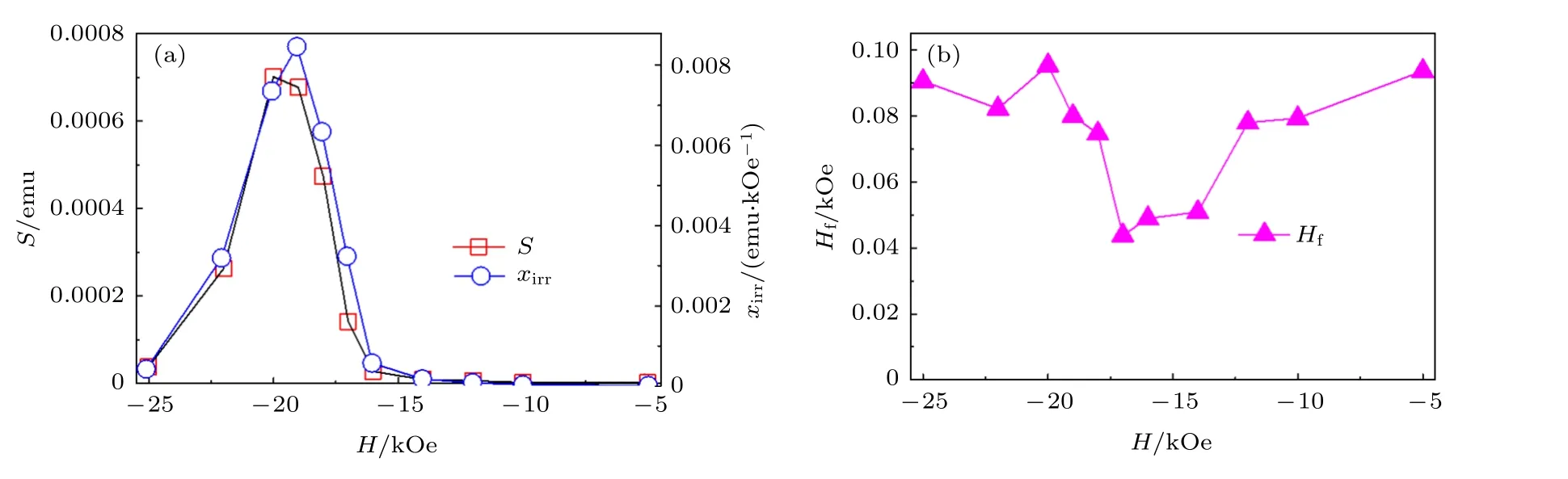
图3 Pr-Fe-B 磁体的(a)磁黏滞系数S、不可逆磁化率xirr 和(b)由公式Hf=S/xirr 得到HfFig.3.(a) Magnetic viscosity coefficient S and irreversible magnetic susceptibility xirr,(b) the fluctuation field obtained by the formula of Hf =S/xirr of Pr-Fe-B magnet.

热扰动引起的反磁化是不可逆磁反转,需要越过一定临界体积即激活体积,激活体积[15]v=kBT/(HfMs),玻尔兹曼常数kB=1.38×10–23J/K,温度T=300 K,饱和磁化强度Ms=1.55 T,Hf在0.04—0.1 kOe (3183—7957 A/m)之间.根据上述数据可得到磁反转临界尺寸v1/3在9.4—6.9 nm 之间,这与磁畴壁尺寸计算公式δ=π(A/K)1/2得到磁畴壁尺寸3.7 nm 处于同一数量级[5,13],这里A为交换积分常数,K为磁晶各向异性场.按公式δ=π(A/K)1/2计算采用了与磁畴壁内自旋矢量旋转一致的近似,而实际自旋角度差在畴壁内中心大、两边逐渐减小,同时在晶粒边界由于缺陷导致磁晶各向异性减小等因素,实际磁畴壁尺寸比理论值大[16].通过热扰动场计算获得的反磁化临界尺寸为纳米级,与实际磁畴壁尺寸近似,这证实热激活反磁化经过磁畴壁形核去钉扎过程[8,9].形核是反磁化降低能量的方式,晶粒边界由于缺陷浓度大,易形成反磁化中心,在外磁场和热扰动作用下,反磁化畴壁形核达到临界尺寸去钉扎实现晶粒反磁化.

如上所述,热扰动效应与反磁化畴壁尺寸密切相关.如图3(b)所示,当反磁化外场小于17 kOe,Hf随磁场增大而减小.由于部分晶粒完成反磁化,已反磁化晶粒由于耦合作用会推动未发生反磁化晶粒磁反转.晶粒之间耦合作用会增大反磁化畴壁尺寸[17],热激活体积增大,依据Hf=kBT/(vMs),热扰动场Hf减小.尽管磁振子具有不确定性,由于实空间的耦合会降低磁振子导致反磁化概率,从而减弱热扰动对反磁化的影响.当外场大于18 kOe,热扰动场Hf增大;这部分晶粒磁晶各向异性场K较大,同时晶间耦合作用有所减弱,依据公式δ=π(A/K)1/2,反磁化形核的畴壁尺寸减小,因而热扰动场增大.

温度升高,热扰动能量kBT增大,磁振子数量增大,其频率分布也有所变化,热扰动场的作用可能也会增强.图4 为120 K 到380 K 磁体热扰动后效场Haf值(等待时间为1200 s)和Haf/Hc比值,但如图4 所示,实测热扰动后效场Haf值随温度上升而降低.纳米晶永磁体晶粒之间耦合作用源于交换积分常数A和磁晶各向异性场K之间的竞争.随着温度升高,Pr2Fe14B 晶体交换积分常数A比磁晶各向异性场K降低幅度小[18],晶粒之间耦合作用更显著,这会增大反磁化临界形核体积,因此热扰动效应会减弱,这应是实测Haf随温度上升稍微降低的原因.温度升高,Pr2Fe14B 晶体磁晶各向异性场减小,磁体矫顽力Hc下降幅度更大,所以Haf与Hc的比值增大,热扰动效应的相对作用在增大.

图4 Pr-Fe-B 磁体从120 K 到380 K 的热扰动后效场Haf 和Haf/Hc 比值Fig.4.Aftereffect field Haf of thermal fluctuation and the ration of Haf and Hc in Pr-Fe-B magnet between 120 K and 380 K.

4 结论

本文对Pr-Fe-B 磁体热扰动反磁化即磁振子宏观效应进行研究,磁振子按能量遵循玻色统计分布率,因此磁振子导致的弛豫反转磁矩与时间自然对数关系可表示为与能量势垒之间的关系.磁振子推动磁矩反转需要越过一定临界体积,即激活体积.激活尺寸与理论磁畴壁尺寸接近,证实热扰动反磁化也需经过磁畴壁形核去钉扎过程.Pr-Fe-B薄带磁体已反磁化晶粒由于耦合作用会推动未发生反磁化的晶粒磁反转,晶间耦合作用会增大反磁化畴壁尺寸,从而导致热激活体积增大,热扰动场Hf值减小.对Pr-Fe-B 薄带的热扰动后效场测量,获得热扰动能量kBT对应矫顽力降低值为0.05 kOe,这与热扰动场测量计算值接近.尽管磁振子具有不确定性,由于实空间的耦合会降低磁振子导致反磁化的概率,从而减弱热扰动对反磁化的影响.