正交像散高密度三维单分子定位显微的数值模拟*

林丹樱 武泽凯 于斌 黄黎琳 张潇 屈军乐

(深圳大学生物医学光子学研究中心/物理与光电工程学院,光电子器件与系统重点实验室,深圳 518060)

单分子定位显微(single molecule localization microscopy,SMLM)成像技术利用荧光分子的稀疏发光、探测及定位,实现了纳米级空间分辨率的超分辨成像.为了提高其时间分辨率,需要提高同时发光的荧光分子密度.但随着分子密度的提高,不同分子的点扩散函数(point spread function,PSF)在探测器上将发生严重的重叠现象,导致空间分辨率降低,尤其是在进行三维SMLM 成像时.为了解决这一问题,本文提出了一种基于正交像散的高密度三维单分子定位超分辨成像方法,并对该方法进行分析和数值模拟研究.该方法的核心是在单分子定位显微镜中将采集的荧光分成两束成像在同一个探测器的两个区域,并在两个通道中各引入一个光学参数相同但取向相互正交的柱透镜,实现对同一个荧光分子正负两个像散PSF 图像的同时探测,然后建立该成像过程的线性投影模型,利用压缩感知算法求解出荧光分子的三维定位信息.结果表明,由于两个正交柱透镜产生的一组正交像散PSF 对作为一个分子的系统响应时具有较低的相关性,该方法的高密度三维定位准确性可显著优于采用单个柱透镜的传统像散方法,且离焦程度越大两个像散PSF 的形状差异越大,这种准确定位的优势就越明显.

1 引言

近十几年来,以随机光学重建显微[1−4]和光激活定位显微[5]为代表的单分子定位显微(single molecule localization microscopy,SMLM)成像技术绕过了光学衍射极限对成像分辨率的限制(约为观察波长的1/2),实现了纳米级空间分辨率的超分辨成像,已被应用于生命科学研究并推动了相关领域的发展.SMLM 利用荧光分子的闪烁,将空间上原本相互重叠的分子像斑—即成像系统的点扩散函数(point spread function,PSF)—在时间上进行分离,进而通过对稀疏PSF 的探测和定位来重构超分辨图像,因此获得一幅超分辨图像通常需要采集数万帧原始图像,时间分辨率很低.

采用高密度成像方法可显著提高时间分辨率.所谓高密度成像,是指以更高的荧光分子密度记录原始图像,从而减少重构一幅超分辨图像所需的原始图像数量.但这样做同时增加了单帧图像中PSF 之间的重叠程度,需要借助更复杂的算法来实现单分子定位.例如多点拟合算法采用多个PSF 模型来拟合,从而提高对重叠分子的识别能力和定位精度[6];压缩感知算法利用分子定位信息满足稀疏先验条件和探测过程的非自适应线性投影关系,采用最优化方法来重构信号[7].目前这些方法在高密度二维单分子定位超分辨成像中已经得到了较好的应用.

然而,高密度三维单分子定位超分辨成像至今仍相对困难.这是因为,三维PSF 不仅在轴向上变化缓慢并呈对称分布,而且体积的扩展使得彼此间更容易发生重叠,导致轴向定位精度低甚至难以定位.目前已有一些方法可以一定程度上实现高密度三维单分子定位成像.例如,2012 年Babcock 等[8]利用单个柱透镜产生的像散破坏三维PSF 的轴向对称性,并采用多点拟合算法进行定位;2014 年Gu等[9]通过同时采集三维PSF 的两个不同焦面,并结合压缩感知算法进行定位;同年,Min 等[10]则将两种方法进行结合,进一步提高了轴向定位精度.这几种方法都较好地实现了高密度三维单分子定位并提高了定位精度,但由于单个分子的三维像散PSF 离焦面较远时其形状变化变得缓慢,这使得定位精度仅能在焦面附近保持较高水平.2015年,Huang 等[11]采用三个焦面互相错开的柱透镜对同一个PSF 产生不同程度的像散,并结合一种快速无偏离连续空间压缩感知算法,较好地解决了轴向定位精度一致性的问题.然而,需要同时对三个焦面错开的三维PSF 进行有效探测使得轴向范围受到了严格的限制,这种三焦面方法的轴向定位范围要小于传统像散法.针对高密度三维单分子定位存在的上述问题,本文提出了一种基于正交像散的高密度三维单分子定位超分辨成像方法,并对其进行了详细的分析和数值模拟研究.

2 成像方法

2.1 成像光路和正交像散原理

图1(a)为正交像散单分子定位成像方法的光路示意图.该方法与传统基于单个柱透镜的像散三维单分子定位成像方法[3]相比,最主要的不同之处在于显微镜采集的荧光信号被均分成传播方向互相垂直的两束,分别经两个探测通道后成像于同一个EMCCD 相机的两个不同区域.图1(a)中,可调光阑A 为两个方向独立可调的矩形光阑,位于显微镜成像透镜的后焦面,用于调节视场大小.两个探测通道中各包含有一个长焦距(1000 mm)柱透镜,两者型号和参数相同但取向相互正交,用于实现对同一个荧光分子的正负两种相反的像散.这样,对于同一个荧光分子,当其处于不同轴向深度z时,将探测到一组正交像散PSF 图像对(如图1(b)所示),同时用于三维定位.

与采用单个柱透镜的传统像散法[3]类似,正交像散法成像时在采集实际样品图像之前需要先利用稀疏分布的荧光珠样品采集图像并制作校准曲线,即对不同轴向深度z处的PSF 在x和y两个方向的宽度进行标定.不同的是,正交像散成像需要4 条校准曲线,对应两个成像通道的两个方向,如图1(c)所示.其中散点数据为利用二维非对称高斯模型对成像系统(采用100×/NA1.45 油浸物镜)采集的不同深度荧光珠(直径100 nm,发射中心波长680 nm)的正交像散PSF 图像进行拟合获得的x和y方向的PSF 宽度wx和wy(取2 倍标准差),实线为多项式拟合[3]结果,拟合参数在后续数据处理时用于待测样品的三维定位.值得指出的是,虽然实际成像系统中两通道的焦面(即wx=wy处)很难做到完全一致,但与多焦面成像方法不同的是,这种错开并不是必须的,因此原则上采用这种方法是可以无需牺牲成像深度的.

图1 正交像散单分子定位成像光路和原理示意图 (a)成像光路示意图;(b)正交像散PSF 图像对;(c)正交像散校准曲线.OL,物镜;DM,二向色镜;EF,发射滤光片;BS,分束器;A,光阑;CL,柱透镜;L,透镜;M,平面镜;EMCCD,电子倍增电荷耦合器件Fig.1.Schematic diagram of the optical path and principle of single molecule localization imaging based on orthogonal astigmatism:(a) Optical path;(b) orthogonal astigmatic PSFs;(c) calibration curves.OL,objective lens;DM,dichroic mirror;EF,emission filter;BS,beam splitter;A,aperture;CL,cylindrical lens;L,lens;M,mirror;EMCCD,electron-multiplying charge-coupled device.

2.2 分子定位及图像重建方法

通过建立上述正交像散成像过程的线性投影模型,可利用压缩感知算法求解荧光分子的三维定位信息.本文所采用的压缩感知算法是在TVSTORM算法[12]的基础上进行改进的.

如前所述,对于样品中的一个荧光分子,EM CCD 将采集到一组正交像散PSF 图像对.因此,设样品中N个荧光分子组成的“源信号”X如(1)式所示,则双通道图像µ(µ=[µ1,µ2])为X与两个PSF 的卷积,可用(2)式表示:

其中θL=(θx,θy,θz)和θI分别为第i个分子的三维坐标和强度;Θ为所有N个荧光分子的这4 个参数的组合;θb为背景噪声;k=1,2 分别对应通道I 和通道II;(u,v)为各通道图像的像素坐标;Φk为对应通道k的观测矩阵,代表位于θL的荧光分子对通道k图像的贡献,可根据正交像散校准曲线构造.因此,单分子定位的任务,就是利用上述模型从实际探测到的双通道图像y(y=[y1,y2])中求解出Θ.考虑到EMCCD 对较弱的单分子荧光的探测满足泊松分布,TVSTORM 算法采用泊松噪声模型来构建损失函数[12].这里,针对正交像散成像,将泊松损失函数L(y|X)定义为

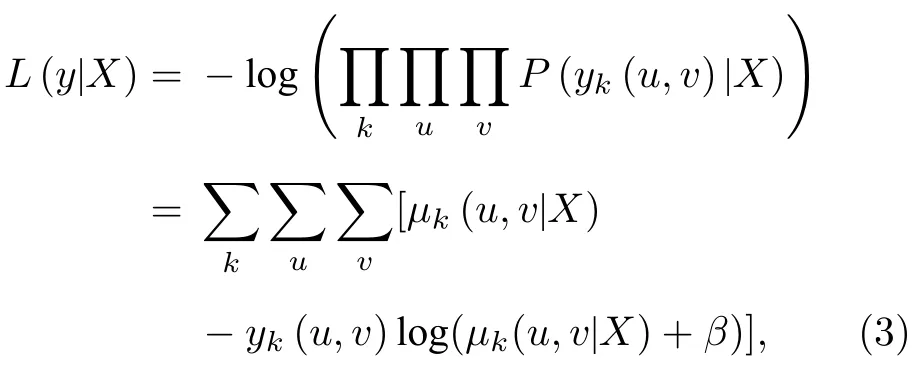
其中,P代表概率,yk和µk分别为通道k的实际图像和根据(2)式计算得到的“理想”图像,0<β ≪1,用于提高对数项的稳定性.

通过最小化该损失函数,可求解(逼近)源信号X的参数Θ,重构出超分辨图像.TVSTORM算法的迭代过程主要包含两层[12]:第一层是从图像中寻找到一个新的荧光分子并初步确定其位置及强度,第二层是进一步优化该分子的定位和强度.针对正交像散法得到的双通道图像.第一层迭代的具体做法是在第n+1 次迭代中,利用第n次迭代得到的已有荧光分子信息(记为Θ(n))和观测矩阵Φ(Φ=[Φ1,Φ2])生成双通道理想图像µ,然后通过最小化泊松损失函数的一阶泰勒近似(如(4)式所示,其中S为双通道图像的图像尺寸),从其中一个通道(k(n+1))的图像中定位到一个新的荧光分子,获得其位置信息,并通过最小二乘准则估计其强度(如(5)式所示),从而得到第n+1 次迭代的结果Θ(n+1),由第二层的迭代进行进一步优化.

第二层采用迭代梯度下降方法,通过最小化(3)式的双通道图像泊松损失函数获得Θ(n+1)的极大似然估计来进一步优化定位结果.其中,下降方向通过分别计算损失函数在x,y,z和I这4 个方向的偏导数来确定,下降步长采用回溯线搜索方法来确定,以加快迭代收敛速度.精炼后的荧光分子信息Θ(n+1)返回第一层并进入下一次迭代,当新增荧光分子的强度低于预设阈值时迭代终止.

3 结果与讨论

3.1 PSF 相关性分析

柱透镜像散法能够实现单分子三维定位的基本原理,是基于不同轴向深度的荧光分子的二维PSF 呈现为不同取向和不同椭圆度的椭圆.因此,两个不同荧光分子的PSF 区别越明显,就越容易被准确定位和分辨.可通过计算两个PSF 之间的相关系数来半定量地表征两个分子能够被准确定位的概率[10].

图2 以伪彩图的形式直观地展示了位于(0,0,z1)和(dx,dy,z2)的两个荧光分子PSF 的相关系数,伪彩色从蓝到红对应相关系数从0 到1.图2(a)对应传统采用单个柱透镜的像散成像,图2(b)对应正交像散成像.值得注意的是,对于正交像散,每个荧光分子的PSF 实际上是一组正交像散PSF图像对(如图1(b)).图2 中第1—3 列为两个荧光分子位于同一深度(z1=z2=–550,0 和550 nm)但横向错开不同距离时的情况,第4 列为两个荧光分子横向位置相同(即dx=dy=0)但分别位于不同深度(z1,z2)时的结果.

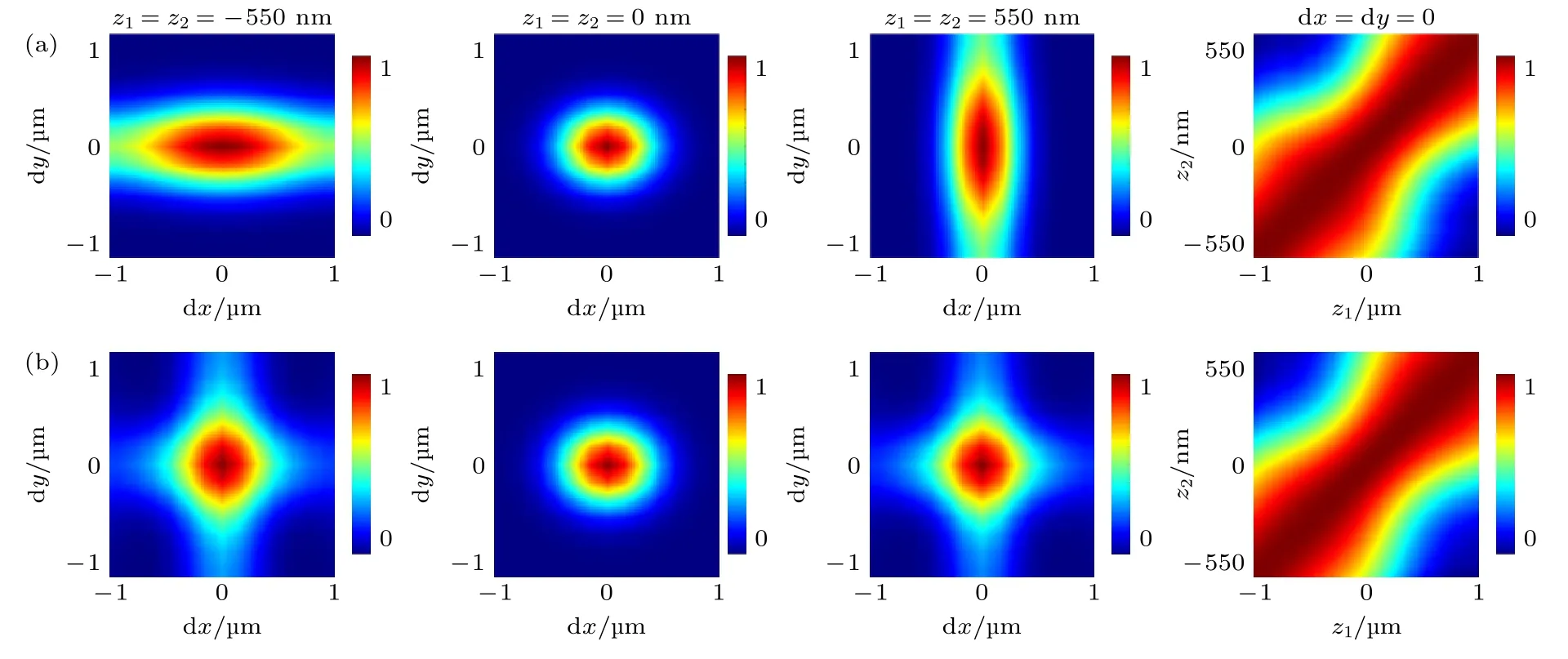
图2 PSF 相关系数 (a)传统像散法;(b)正交像散法Fig.2.Mutual correlation values between PSFs:(a) Traditional astigmatic method;(b) orthogonal astigmatic method.

可以看出,当离焦较远时,两种成像模式得到的PSF 相关性有很大差异.采用传统像散法时,在焦面以下550 nm 处,x方向错开了将近2 µm 的两个PSF 相似程度依然较高,难以准确定位;反之,在焦面以上550 nm 处的两个PSF 则是在y方向相似程度较高不易定位.这与之前文献中关于像散法在两个方向上分辨能力不同的报道[13]是符合的,是由加入柱透镜后两个方向的实际焦面位置不同导致的.但当采用正交像散成像方法时,这种情况得到了很大程度的改善,即不管是在焦面以上还是以下,PSF 的相关性在x和y两个方向变得更加对称,且总体要明显低于传统像散法,说明采用这种方法在离焦较远时仍能得到相似程度较低的PSF 对,从而为准确定位距离较近的荧光分子提供了条件,提高了系统的高密度定位能力.

3.2 数值模拟实验

为定量评估该正交像散成像方法的性能,基于图1(c)中的校准曲线进行数值模拟实验研究.在模拟实验中,利用校准曲线产生一系列三维位置随机的PSF 来模拟实验中采集的原始图像.图3(a)所示为模拟实验产生的正交像散成像的单帧双通道闪烁图像,图像大小32×32 像素/通道,像素尺寸160 nm×160 nm,荧光分子密度1/µm2,单个PSF 的探测光子数为500/通道,并添加泊松噪声.图中黑色小叉表示随机生成的“分子”的横向位置,其轴向深度则体现在PSF 的形状上.作为对比的传统像散法模拟时采用通道I 的闪烁图像,但光子数设置为1000.

图3 单帧双通道图像及定位结果 (a)单帧双通道图像;(b)正交像散法定位结果;(c)传统像散法定位结果Fig.3.Single frame image and localization results:(a) Single frame of two-channel image;(b) localization results using orthogonal astigmatic method;(c) localization results using traditional astigmatic method.

3.2.1 三维定位结果的直观比较

利用前述算法对该单帧闪烁图像中的PSF 对进行定位,结果如图3(b)所示,其中两个图像分别显示了定位结果与两个通道的原始图像之间的对比.作为对照,图3(c)给出了采用传统像散成像的定位结果.图中黑色小叉仍代表模拟图像中“分子”的真实横向位置,白色小椭圆中心代表横向定位结果,其与黑色小叉重合的程度直观表示横向定位的准确性;虚线黑色椭圆和实线白色椭圆分别代表根据已知的轴向深度和轴向定位结果得到的PSF 形状(依据校准曲线),两者的相似程度直观表示轴向定位的准确性.对比图3 结果可以看出,采用正交像散法可显著提高三维定位的准确性,尤其是在PSF 重叠程度较大(即局部密度较高,如图3(c)中黑色箭头所指区域),或PSF 椭圆度较高的情况下(即离焦较远,如图3(c)中白色箭头所指),准确定位的优势更加明显,说明该方法适用于处理高密度数据,且对于离焦较远的分子会有更好的定位效果,与前面的分析是一致的.

3.2.2 不同轴向深度定位结果的统计分析

为了定量分析定位性能,可产生若干帧模拟闪烁图像并重复上述定位过程,计算各“分子”的定位坐标与真实坐标之间的均方根误差(root mean squared error,RMSE),以定量描述定位的准确性.计算公式如下:

其中,j=x,y,z,N表示定位得到的分子总数;(θxi,θyi,θzi)表示第i个分子的定位坐标;(θxi0,θyi0,θzi0)表示其真实坐标.

图4 给出了位于不同轴向深度的“分子”沿各方向定位的RMSE 值,并与传统像散法定位结果进行对比.模拟实验中同一帧闪烁图像不同“分子”的横向位置设置为随机,但轴向深度设置为相同(如200 nm),荧光分子密度固定为1/µm2,每个深度处累计定位1000 帧.从图4 可以明显看出,采用正交像散法相比传统像散法,离焦“分子”在3 个方向的定位准确性均有显著提高,尤其是焦面以下x方向定位准确性和焦面以上y方向定位准确性的提高,与前面的PSF 相关性分析是完全符合的,进一步验证了该方法对于离焦较远的分子会有更好的定位效果的结论.除了RMSE,图4 还给出了定位召回率和错误率的比较,同样可以看出正交像散法要明显优于传统像散法.

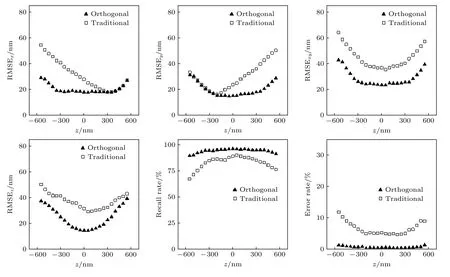
图4 不同轴向深度分子定位准确性、召回率和错误率比较Fig.4.Comparison of localization accuracy,recall rate and error rate of molecules with different axial depths.

3.2.3 不同荧光分子密度定位结果的统计分析

此外,为了更好地表征正交像散法对于高密度数据的定位性能,图5 给出了不同分子密度下的各方向定位的RMSE 值及定位召回率和错误率的比较.其中,模拟实验中不同“分子”的三维位置均设置为随机,每个分子密度下累计定位1000 帧.从图5 可以明显看出,与传统像散法相比,正交像散法在分子密度越高时优势越明显,说明该方法适用于高密度数据的处理.

图5 不同密度分子的定位准确性、召回率和错误率比较Fig.5.Comparison of localization accuracy,recall rate and error rate of molecules with different densities.

3.2.4 模拟样品的超分辨图像

为了更直观地展示正交像散法的超分辨成像效果,以一些特定结构作为模拟样品,按照前述相同方法产生正交像散闪烁图像进行定位和超分辨重构.图6 给出了螺旋线的三维定位超分辨图像.其中,图6(a)和图6(b)分别为正交像散和传统像散两种方法得到的结果.螺旋线半径为1200 nm,相邻层轴向距离为400 nm.从图6 可以直观地看出,采用传统像散法在远离焦面时,在螺旋线以外存在很多不准确的定位点,而采用正交像散法则能在整个轴向探测范围内更加准确地还原出螺旋线的结构.

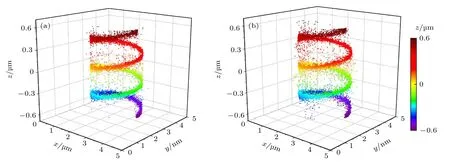
图6 螺旋线的模拟成像结果 (a)正交像散法;(b)传统像散法Fig.6.Simulated imaging results of a helix structure:(a) Orthogonal astigmatic method;(b) traditional astigmatic method.

图7 所示的是6 组平行线的模拟超分辨成像结果.其中,x方向和y方向平行线的间距从小到大分别为50,100 和150 nm,平行线的轴向深度连续变化,如图中伪彩色所示.图7(a)和图7(b)分别对应正交像散和传统像散两种方法.从图7 可以看出,两种方法都能够清晰地分辨出间距150 nm的平行线,但随着间距越来越小,在轴向深度离焦较远时,传统像散法的图像开始变得模糊,而正交像散法则依然可以清楚地分辨出两条平行线.图7(c)—图7(f)是距离50 nm 的两组平行线的放大图.可以直观地看出,采用传统像散法在轴向深度约大于400 nm 时,y方向的分辨能力开始变得很差,因此x方向的平行线变得几乎无法分辨(图7(d)绿色方框所示),而焦面另一侧的情况则刚好相反(图7(f)黄色方框所示).但是采用正交像散法时,x和y两个方向上均能清楚地分辨出两条平行线(图7(c)和图7(e)中对应的方框所示).对方框区域内的定位结果进行y方向或x方向(即垂直于直线方向)的双峰拟合,可得到正交像散成像时两组平行线双峰间距分别为46 和48 nm,与模拟时设置的真实值50 nm 很接近,可见正交像散法在离焦较远的情况下仍能准确得到三维定位信息.

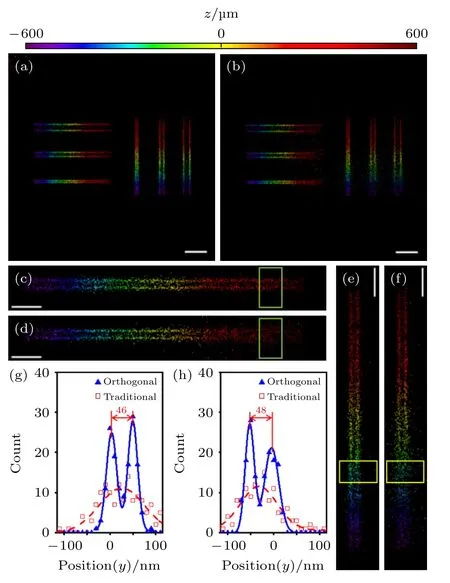
图7 平行线的模拟成像结果 (a),(c),(e)正交像散法;(b),(d),(f)传统像散法;(c)—(f)间距最小(50 nm)平行线的放大图;(g)图(c)和(d)的绿色方框区域的强度分布曲线;(h)图(e)和(f)的黄色方框区域的强度分布曲线.标尺大小:(a),(b) 500 nm;(c)—(f) 200 nmFig.7.Simulated imaging results of parallel line structures:(a),(c),(e) Orthogonal astigmatic method;(b),(d),(f) traditional astigmatic method;(c)–(f) zoomed-in view of the minimum spacing (50 nm) lines;(g) cross-sectional profiles of the green boxes in panel (c) and (d);(h) cross-sectional profiles of the yellow boxes in panel (e) and (f).Scale bars:(a),(b) 500 nm;(c)–(f) 200 nm.

3.2.5 双通道图像偏差的影响分析

在实际的成像实验中,尽管在光路调节上可以尽量保证两个成像通道的一致性,但两个通道采集到的图像之间仍不可避免地会存在偏差,包括横向偏移、旋转和缩放等,从而影响正交像散成像三维定位的准确性.图8 给出了双通道图像偏差对正交像散法横向和轴向定位RMSE 值的影响分析,以及经过图像配准之后的定位重构结果.其中图8(a)分别为通道II 图像相比通道I 图像存在不同横向偏移量Δx、旋转角度α和缩放倍数Γ时xy方向和z方向定位的RMSE 值.荧光分子密度固定为1/µm2,轴向深度在–600—600 nm 之间变化.可见,双通道图像之间的这几种偏差,都会导致定位精度不同程度的降低.因此,两个成像通道采集的图像需要先进行配准,以尽量消除两通道图像之间的不匹配导致的定位精度下降.这里采用常用的傅里叶-梅林变换法对双通道图像进行配准[10,11],并对配准效果进行模拟分析.图8(b)为一组存在双通道图像偏差并经过配准后的正交像散成像模拟结果,其中双通道原始图像偏差设为Δx=320 nm,α=2°,Γ=0.95.利用双通道荧光珠图像进行配准,得到配准参数分别为Δx'=–352 nm 和Δy'=–41 nm,α'=–1.9125°,Γ'=1/0.9505.作为对比,图8(c)给出了双通道图像不存在任何偏差时的模拟成像结果.可以看出,存在双通道偏差的图像数据配准后仍能很好地重构出超分辨结构,但由于图像配准后仍有一定误差(如横向偏移配准精度约为30—40 nm),因此与理想无偏差情况相比,定位效果略有下降.从图8(a)的定量结果还可以看出,配准误差导致的RMSE 值的改变幅度已经很小,而采用具有更高配准精度的方法还可以进一步减少双通道图像偏差对定位的影响.

图8 双通道图像偏差的影响和有无图像偏差及配准的模拟成像结果比较 (a)定位准确性随横向偏移量、旋转角度和缩放倍率的变化;(b)有偏差双通道图像配准后的模拟成像结果;(c)无偏差双通道图像的模拟成像结果.标尺大小:500 nmFig.8.Influence of deviation between two channel images,and comparison of simulated imaging results with and without image deviation and registration:(a) Localization accuracy versus lateral offset,rotation angle and scaling ratio;(b) simulated image obtained after registration of biased dual channel images;(c) simulated image of unbiased dual channel images.Scale bars:500 nm.

4 总结与展望

针对高密度三维单分子定位中PSF 重叠导致的定位能力下降的问题,发展了一种基于正交像散的高密度三维单分子定位超分辨成像方法.详细阐述了该正交像散单分子定位成像方法的原理和实现过程,并对该成像方法进行了分析和数值模拟研究.结果表明,利用该方法可以在无需牺牲成像深度的前提下显著提高离焦荧光分子的三维定位精度.其根本原因在于,采用正交像散法时一个荧光分子对应一组正交像散PSF 图像对,离焦情况下这一组自身形状差异很大的PSF 对作为一个整体,与另一个分子的PSF 对之间具有比单独的PSF图像更低的相关性.换句话说,采用两个取向相互正交的柱透镜,可以一定程度上抵消x和y方向的两个焦面分别位于成像焦面两侧对单分子定位的影响,从而提高高密度三维定位能力.

在实际的成像实验中,两个成像通道之间总是不可避免地会存在偏差,因此除了在光路上尽量保证两个成像通道的一致性之外,对于两个通道采集到的图像通常需要先进行配准,以尽量消除两通道图像的不匹配导致的定位精度下降.在此基础上,考虑两个成像通道之间引入的不同像差,以及因成像在探测器的不同区域而导致的微小差别,分区域进行配准,将有利于进一步提升双通道图像之间的配准精度,从而消除实际实验中存在的双通道图像偏差对定位精度的影响.