过渡金属原子X (X=Mn,Tc,Re) 掺杂二维WS2 第一性原理研究*

陈蓉 王远帆 王熠欣 梁前 谢泉

(贵州大学大数据与信息工程学院,新型光电子材料与技术研究所,贵阳 550025)

二维材料由于具有独特的电子结构和量子效应、丰富的可调控特性而受到凝聚态物理和材料科学的广泛关注,其中通过过渡金属掺杂二维WS2 形成的半金属铁磁性材料在自旋电子学领域中发挥着重要的作用.采用基于密度泛函理论的第一性原理赝势平面波方法计算了过渡金属原子X (X=Mn,Tc,Re) 掺杂二维WS2的电子结构、磁性和光学性质.研究表明:被过渡金属原子X 掺杂的WS2 体系在S-rich 条件下比在W-rich 条件下更稳定.在 Mn 掺杂后,自旋向上通道中出现杂质能级,导致WS2 体系从自旋向上和自旋向下态密度完全对称的非磁性半导体转变为磁矩1.001 μB 的铁磁性半金属.在Tc,Re 掺杂后,体系均转变为非磁性N 型半导体.所有掺杂体系杂质态均发生自旋劈裂现象,且自旋劈裂程度逐渐减小.同时发现 Mn,Tc,Re 掺杂后,表现出优异的光学性质,它们的介电常数和折射系数与未掺杂WS2 的体系相比明显增强,吸收系数在低能量区域 (0—2.0 eV) 均出现红移现象.

1 引言

自旋电子学作为一种革命性的替代技术是当前国内外研究的热点问题.自旋电子学具有能耗更低、数据处理速度更快、集成度更高等优点,它利用新手段同时调控电子自旋自由度和电荷自由度并将其应用到电子器件中,可构造自旋场效应晶体管、自旋发光二极管和磁存储器件等[1].当然,最重要的自旋电子特性体现在半金属铁磁性 (halfmetal ferromagnetism,HMFM) 材料上[2],在半金属磁体的能带结构中,两个自旋子能带分别具有不同的导电特性,从而产生自旋完全极化的传导电子,这一特性使其有可能在新一代微电子设备中发挥重要作用,并为极化传输理论及自旋电子学的研究开辟崭新的领域[3,4].

近年来随着石墨烯[5−8]等二维层状纳米材料研究热潮的兴起,一种新型的类石墨烯二维过渡金属二硫化物 (TMDs) 引起了物理、化学、材料、电子等众多领域研究人员的广泛关注[9−16].二维 WS2是TMDs 材料的典型代表,其制备方法也从单一的机械剥落法,发展至液相剥落、化学剥落、超临界流体剥落、化学气相沉积和外延生长等[17,18].二维WS2在过去常被用作润滑剂[19],但随着对其研究的不断深入,二维WS2已在电子器件领域有了一席之地,WS2的异质结构[20]、杂化材料、掺杂材料等功能化复合材料[21,22]被不断地开发出来,且被证实其性能及功能基本上都要优于单一的二维WS2.Zhang 等[23]研究了一种基于Ni 掺杂In2O3/WS2异质结的高性能甲醛传感器,发现与In2O3,WS2及其复合材料相比,Ni-In2O3/WS2传感器的甲醛检测性能显著提高,还通过密度泛函理论模拟,探讨了Ni-In2O3/WS2薄膜传感器对甲醛的敏感机理.Zhou 等[24]通过构造WS2/CsPbBr3的范德瓦耳斯异质结构来调控界面应变,发现在1.70 V 的超高开路电压下,器件的效率达到10.65%,在持续120 d 的光照射下稳定性显著提高.Kang 等[25]利用扫描透射电子显微镜通过化学气相沉积将过渡金属Fe 原子掺入二维MoS2与WS2体系,并使用氮空位中心磁强计和超导量子干涉仪对体系进行测量,发现Fe 掺杂WS2单分子层具有深能级陷阱态,而Fe 掺杂MoS2单分子层中具有浅能级陷阱态.Xiao 等[26]采用基于密度泛函理论的第一性原理计算研究了MoS2和WS2纳米带的磁性能,发现MoS2和WS2层状纳米带的带隙能随着层数的增加而单调递减,宽度为0.36 nm 的单层MoS2纳米带为磁性半导体,而锯齿型MoS2和WS2纳米带都具有磁性和金属性质.Xie 和Zhang[27]利用第一性原理计算研究了重金属原子X(X=Au,Hg,Tl,Pb)掺杂单层WS2体系,发现Au 和Hg 原子掺杂的单层WS2体系变成了半金属铁磁体,磁矩分别为0.697 μB和1.776 μB.Wang 等[28]运用第一性原理计算探究了Co-X(X=B,C,N,O,F) 掺杂WS2,发现Co-O 共掺WS2体系呈现半金属铁磁特性.过往的研究表明,3d 过渡金属元素掺杂二维WS2在其物理性质以及表面催化等领域都有显著的效果和丰富的应用前景[29,30].由于3d 过渡金属元素中只有Cr 元素与Mn 元素的磁性为反铁磁性,且Mn 元素属于与W 元素邻近的ⅦB 族元素,其中Mn 元素磁性为反铁磁性,Tc 与Re 元素磁性为顺磁性,表明ⅦB 族元素有较特殊的磁性质差异.鉴于过渡金属ⅦB 族原子X(X=Mn,Tc,Re) 掺杂二维WS2还尚未有研究,因此,本文对二维WS2进行替位式掺杂,研究ⅦB 族过渡金属原子X(X=Mn,Tc,Re) 掺杂WS2体系的磁性、电子结构和光学性质.

2 计算方法与理论模型

本文使用VASP (Viennaab initiosimulation package) 程序包[31]基于密度泛函理论的投影缀加平面波(PAW) 方法,并采用广义梯度近似下的PBE (Perdew-Burke-Emzerhof) 泛函来描述交换关联效应[32].在晶格弛豫计算过程中,使作用在每个离子上的力小于0.05 eV/Å (1 Å=0.1 nm),并且当连续两个电子步之间的能量差小于1×10–6eV时停止弛豫,完成晶格优化;平面波截断能选为400 eV,在对布里渊区进行积分运算时,选择了由Monkhorst-Pack 方案生成的9×9×1 的K点网格.过渡金属原子X(X=Mn,Tc,Re)掺杂二维WS2体系的俯视图和侧视图如图1 所示.计算体系选取3×3×1 共27 个原子的WS2超胞结构作为研究对象,用过渡金属X(X=Mn,Tc,Re)原子替换其中一个W 原子.建模时在c轴方向加上20 Å的真空层,为了屏蔽结构的周期性重复对相邻结构的影响.

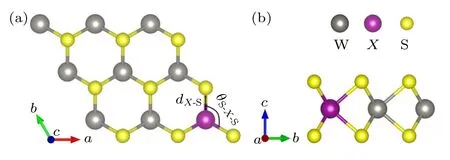
图1 过渡金属原子X (X=Mn,Tc,Re) 掺杂二维WS2 的结构 (灰色球、紫色球和黄色球分别表示W,X 和S 原子) (a) 俯视图;(b) 侧视图Fig.1.Structure of transition metal atom X (X=Mn,Tc,Re) doped two-dimensional WS2 (the gray,purple,and yellow balls denote W,X and S atoms,respectively):(a) Top view;(b) side view.

3 结果与讨论

3.1 结构与稳定性

2H相WS2由S-W-S 三原子薄层堆叠而成,空间群为P63/mmc并具有1.3 eV 的间接带隙.原子之间通过较强的共价键结合在一起,两个单层之间通过范德瓦耳斯力相互作用.弱耦合使得2H相WS2像石墨烯一样易剥离为1T相单层WS2,由于反演对称性的破缺,其空间群转变为Pm2,且带隙转变为1.81 eV 的直接带隙[33].表1 列出了未掺杂与掺杂二维WS2体系优化后的晶格常数a(a=b),掺杂原子X和S 原子之间的键长dX-S,W 原子或者掺杂原子X最近邻的两个S 原子间的键角θS-X-S,以及掺杂WS2体系在S-rich (硫元素为多数元素) 和W-rich (钨元素为多数元素)条件下的形成能Eform,图1 中标示出了dX-S和θS-X-S.通过计算发现未掺杂WS2体系优化后的晶格常数a=b(3.182 Å)、键长dW-S(2.416 Å) 和键角θS-W-S(82.351°) 与Zhu 和Zhang[34]所计算的理论结果非常吻合,证明本文的计算方法具有可靠性.由于在ⅦB 族中,Tc 原子和Re 原子半径近似且大于Mn 原子半径,所以Tc 和Re 掺杂体系的晶格常数a(a=b)、键长dX-S和键角θS-X-S均大于Mn掺杂体系.

表1 未掺杂、掺杂二维WS2 的体系优化后的晶格常数a (a=b)、键长dX-S、键角θS-X-S 以及体系在S-rich 和W-rich条件下的形成能EformTable 1. Optimized lattice constants a (a=b),bond lengths dX-S,bond angles θS-X-S,and formation energies Eform of the system under S-rich and W-rich conditions for the undoped and doped two-dimensional WS2 systems.

形成能是体现掺杂后二维WS2体系相对稳定性的标准之一,定义如下[35,36]:

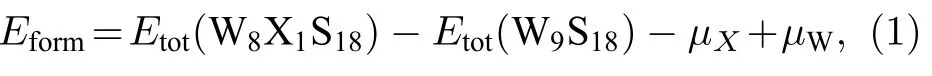
其中Etot(W9S18) 和Etot(W8X1S18) 分别表示未掺杂和掺杂后WS2体系总能量;µX表示掺杂原子X的化学势,且µX等于掺杂原子块体结构中每个X原子的总能量;µW表示主体原子W 的化学势,并且µW依赖于两种不同的条件S-rich 和W-rich.化学势是一个约束条件,不能任意取值.根据材料生长条件,W 元素和S 元素的化学势是彼此约束的,所以进行了不同生长条件下W 原子化学势的讨论,定义如下[37]:

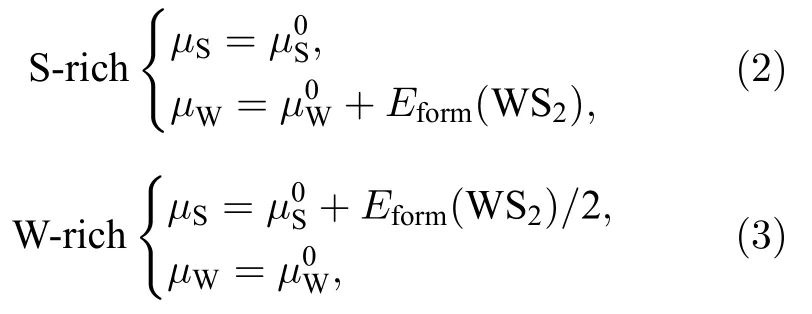
式中和分别表示的是每个S 原子在硫单质和每个W 原子在体心立方结构中的总能量.此外,Eform(WS2)是二维WS2的形成能,其定义如下[35,36]:

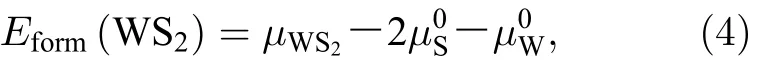
其中µWS2表示WS2化学势,且µWS2等于Etot(W9S18)超胞总能量的1/9.

形成能越低表明体系越稳定.表1 列出了掺杂后二维WS2体系的形成能,在S-rich 条件下,过渡金属(TM)原子Mn,Tc,Re 掺杂二维WS2体系的形成能分别为–0.662 eV,–1.292 eV 和–0.668 eV,而在W-rich 条件下,各体系形成能分别为1.810 eV,1.180 eV 和1.804 eV.在这两种条件下,Tc 掺杂二维WS2体系的形成能都是最低的.同时可以看出,这3 种掺杂体系的形成能在S-rich 条件下与W-rich 条件下相比,S-rich 条件下的形成能更低且在此条件下掺杂体系结构更容易形成.

3.2 磁性质与电子结构

3.2.1 磁性质

表2 列出了未掺杂WS2与掺杂WS2体系的总磁矩Mtot,TM 原子X的局部磁矩MX,与TM原子X最近邻S 原子的局部磁矩MS,与TM 原子X最邻近W 原子的局部磁矩MW.从表2 可以看出,未掺杂的WS2没有磁矩,因此可说明此体系为非磁性.由于Mn 原子具有反铁磁性,采用自旋极化计算得出的Mn 掺杂体系总磁矩Mtot为1.001 μB,掺杂体系的总磁矩主要由TM 原子Mn 所贡献,磁矩主要集中在掺杂Mn 原子上,且Mn 原子局部磁矩MX为1.087 μB.又由于Tc 与Re 原子具有顺磁性,经过计算所得的Tc 与Re 掺杂体系没有磁矩,表明这两个掺杂体系没有磁性,这也与接下来要讨论的能带结构和态密度所对应.

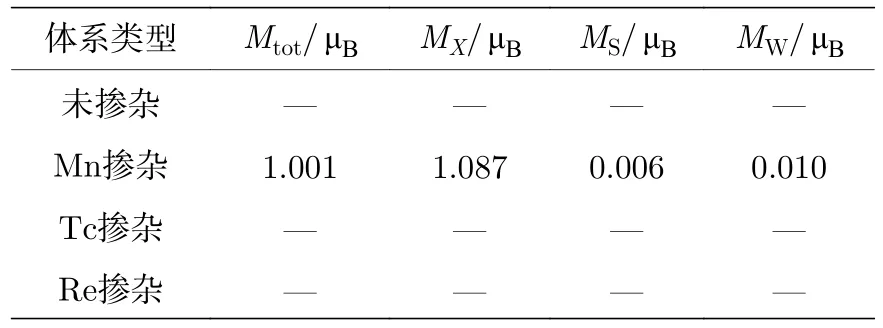
表2 未掺杂与掺杂二维WS2 体系的总磁矩Mtot、TM 原子X 的局部磁矩MX、与TM 原子X 最近邻S 原子的局部磁矩MS 以及与TM 原子X 最邻近W 原子的局部磁矩MWTable 2. Total magnetic moments Mtot,the local magnetic moments MX of TM atom X,the local magnetic moments MS of nearest S atom to TM atom X and the local magnetic moments MW of nearest W atom to TM atom X for undoped and doped two-dimensional WS2 systems.

3.2.2 能带结构

为了分析TM 原子X(X=Mn,Tc,Re)掺杂二维WS2体系能带结构的变化情况,本文将WS2超胞结构和掺杂体系的能带结构进行了对比,能量范围为–3.0—2.5 eV,如图2 所示.表3 列出了自旋向上通道的带隙和自旋向下通道的带隙以及体系的磁特性与导电特性.图2(a)是未掺杂二维WS2体系,具有1.813 eV 的直接带隙,自旋向上通道和自旋向下通道完全一致,表明该体系是典型的非磁性半导体,这与Zhu 和Zhang[38]的计算结果一样.图2(b)是Mn 掺杂体系,与未掺杂WS2体系相比带隙中出现杂质能级,费米能级(EF)穿过自旋向上通道中的杂质能级,但自旋向下通道仍然表现出带隙为1.125 eV 的半导体特性,两个自旋子能带分别具有不同的导电特性,因此它呈现半金属铁磁性.图2(c)是Tc 掺杂体系,自旋向上通道和自旋向下通道完全一致,表明体系没有磁性.Tc 杂质在W 中电离时,能够释放电子而产生导电电子并形成正电中心,说明Tc 为施主杂质.杂质电离以后,导带中的导电电子增多,增强了半导体的导电能力.EF穿过导带底的杂质能级,整个体系为具有直接带隙1.416 eV 的N 型半导体.图2(d)是Re 掺杂体系,与Tc 掺杂体系相同,Re 掺杂体系没有磁性,且Re 为施主杂质,EF穿过导带底的杂质能级,整个体系为具有直接带隙1.516 eV 的N 型半导体.此外,TM 原子Mn,Tc,Re 掺杂WS2体系的两个通道的电子能带结构整体移向低能区,这是由于掺杂原子的质子数逐渐增加,相应对价电子吸引力也逐渐增强.

表3 自旋向上通道的带隙 、自旋向下通道的带隙 、体系的磁特性以及导电特性Table 3. Band gaps in the spin-up channel ,spin-down channel ,the magnetic and electronic properties.

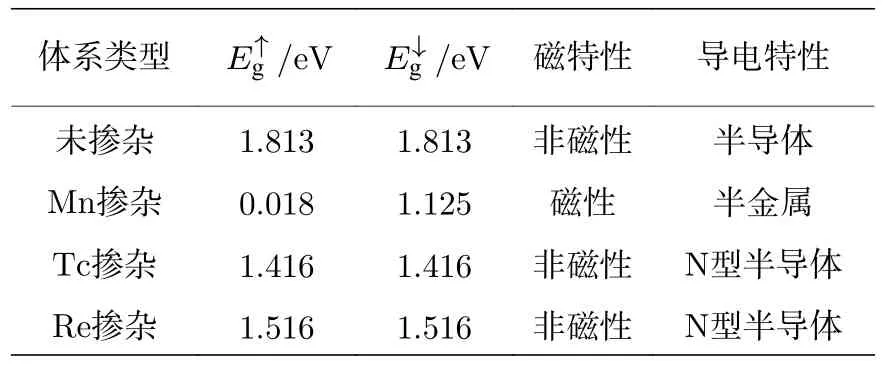
表3 自旋向上通道的带隙 、自旋向下通道的带隙 、体系的磁特性以及导电特性Table 3. Band gaps in the spin-up channel ,spin-down channel ,the magnetic and electronic properties.

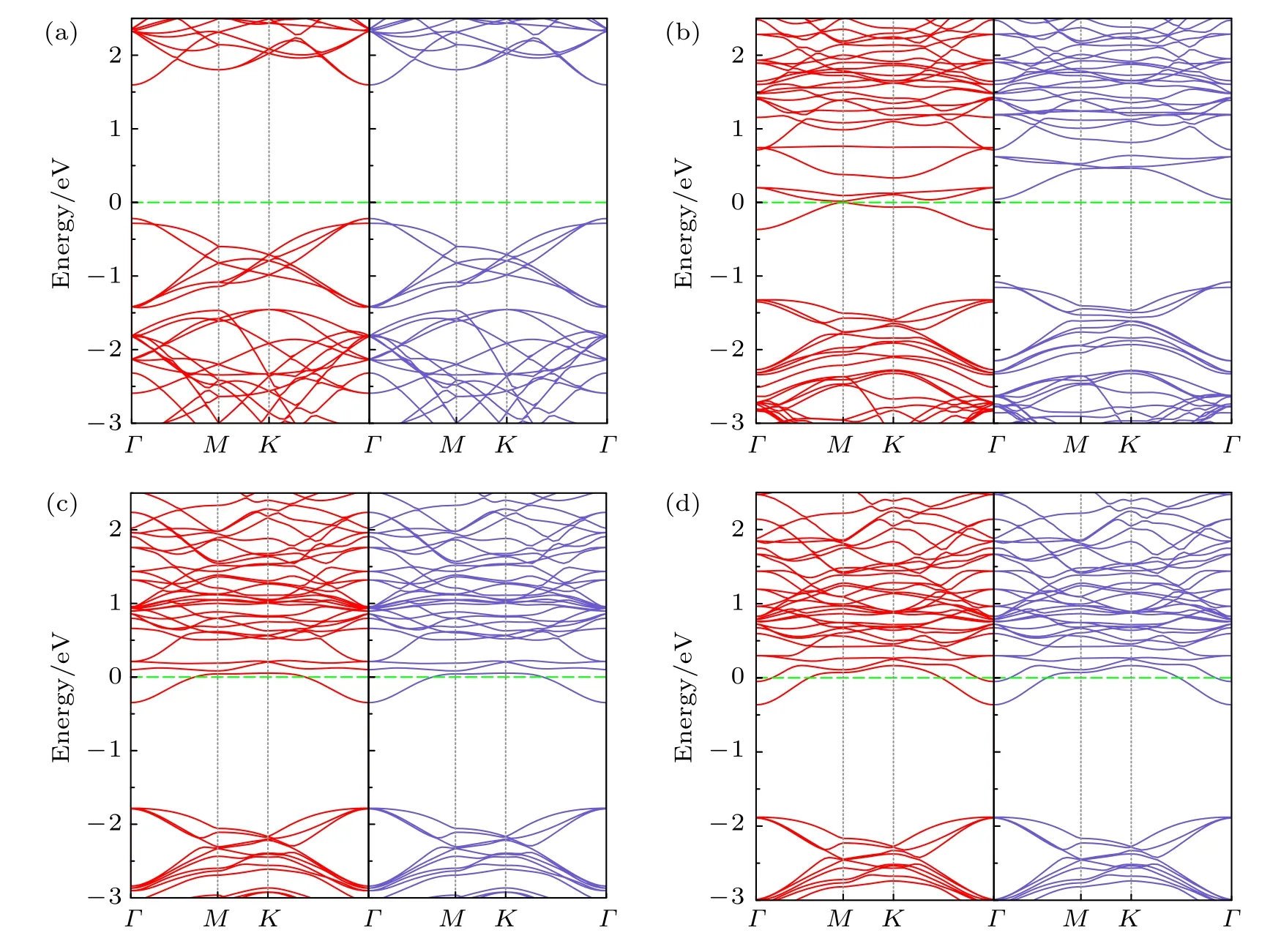
图2 能带结构(红色表示上自旋电子能带,蓝色表示下自旋电子能带,绿色水平虚线代表EF 为零值) (a) 二维WS2;(b) Mn 掺杂;(c) Tc 掺杂;(d) Re 掺杂Fig.2.Energy band structures (The red lines indicate spin-up electron energy band,the blue lines indicate spin-down electron energy band,the green horizontal dashed lines represent zero value of Fermi energy level EF):(a) Two-dimensional WS2;(b) Mn doped;(c) Tc doped;(d) Re doped.

3.2.3 态密度

图3 给出了未掺杂二维WS2以及TM 原子X(X=Mn,Tc,Re) 掺杂二维WS2体系的总态密度(total density of states,TDOSs)和分波态密度(partial density of states,PDOSs).能量范围为–3.0—2.5 eV,与能带结构中所选择的范围一致.如图3(a)所示,在未掺杂WS2体系中,TDOSs 的贡献主要来自W-5d 轨道电子和S-3p 轨道电子,自旋向上和自旋向下的态密度是完全对称的,因此呈现出非磁性半导体特征.图3(b)为Mn 掺杂体系由于电子之间的交换作用,在费米能级EF附近传导电子属于同一种自旋的子能带,传导电子都具有相同的自旋方向,自旋向上和自旋向下的态密度发生了自旋劈裂[39],部分占据的杂质态仅在自旋向上通道中出现,说明在该费米能级具有完全自旋极化的半金属铁磁特性,且自旋向上与自旋向下的电子数目不等,在Mn-3d 轨道中形成未被抵消的自发磁矩,因而发生自发磁化.在靠近导带底的位置出现了明显的杂质能级,其TDOSs 主要由W-5d,S-3p 和Mn-3d 轨道电子贡献.图3(c)为Tc 掺杂体系,自旋向上与向下的态密度相互对称,其TDOSs主要由W-5d,S-3p 和Tc-4d 轨道电子贡献,部分占据与非占据的杂质态分别出现在自旋向上和自旋向下的通道中,EF穿过导带底的杂质带,整体呈现非磁性N 型半导体特性.图3(d)为Re 掺杂体系,自旋向上与向下的态密度相互对称,其TDOSs主要由W-5d,S-3p 和Re-5d 轨道电子贡献,EF穿过导带底的杂质带,整体呈现非磁性N 型半导体特性.

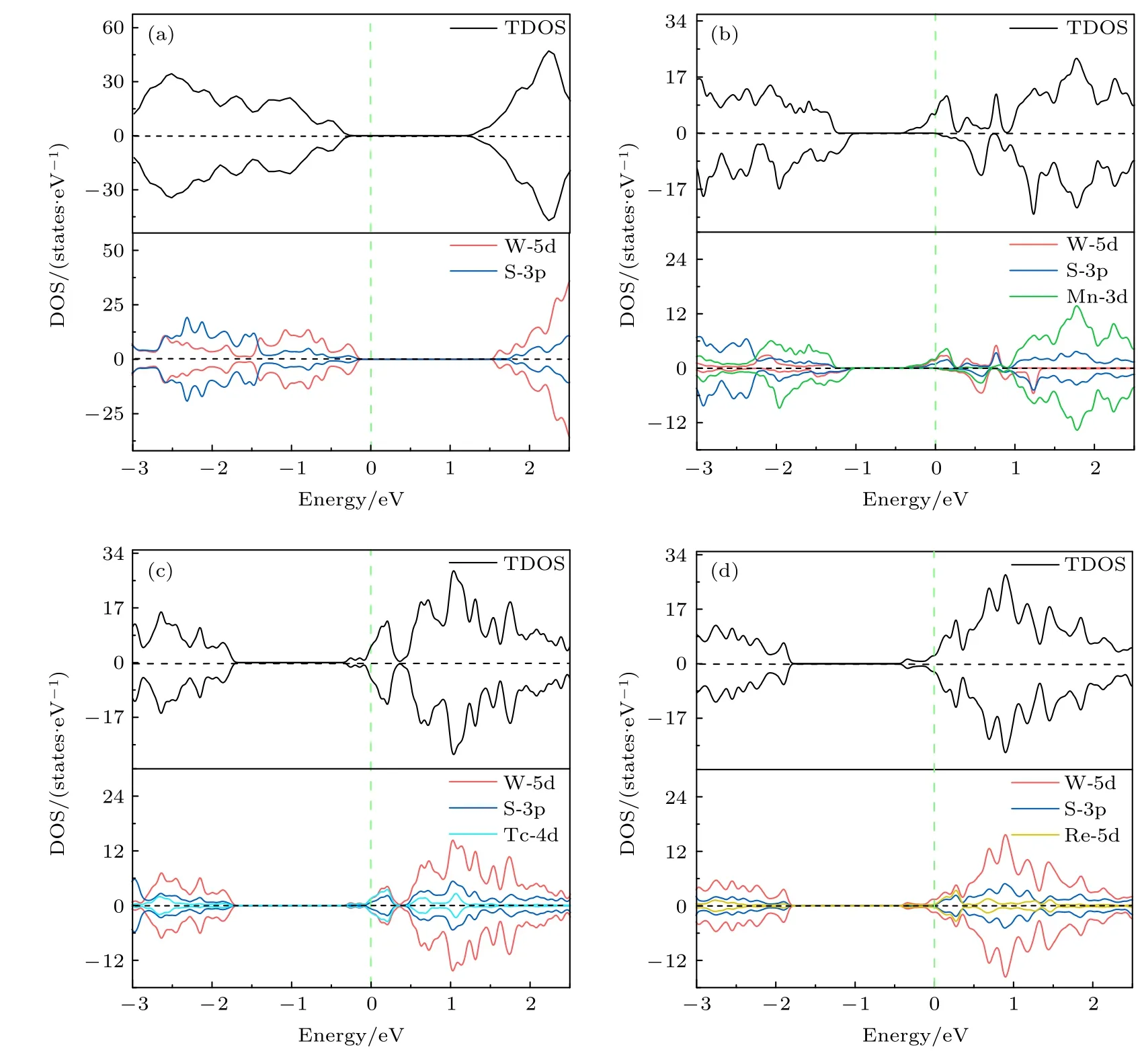
图3 TDOSs 与 PDOSs (a) 二维WS2;(b) Mn 掺杂;(c) Tc 掺杂;(d) Re 掺杂Fig.3.The TDOSs and PDOSs:(a) Two-dimensional WS2;(b) Mn doped;(c) Tc doped;(d) Re doped.

3.3 光学性质

对于未掺杂二维WS2体系,在掺入ⅦB 族过渡金属原子以后,由于Mn,Tc,Re 磁性的差异,导致体系从非磁性半导体特性过渡到非磁性N 型半导体,这明显增大了材料的光学响应度.另外需要注意的是,本文计算光学性质采用的是基于密度泛函理论中求解Kohn-Sham 方程和波函数的计算,忽略了电子-空穴对相互作用,并且计算得出的介电函数和光学性质包含了二维材料和真空层的综合作用,计算结果仅作定性的趋势讨论.Yang和Gao[40]提出了一种通过恢复二维材料固有介电函数使其不受额外真空层影响的方法,能够准确预测二维材料的介电函数和光学性质.经过计算发现c轴方向掺杂的引入对光学性质的影响并不明显.因此,本文研究了未掺杂WS2和Mn,Tc,Re掺杂WS2体系在0—11 eV 能量范围内垂直于c轴方向的复介电函数ε(ω)ε1(ω)+iε2(ω) (其中ε1(ω)为实部,ε2(ω) 为虚部),折射系数n(ω) 以及吸收系数α(ω),表达式如下[41]:

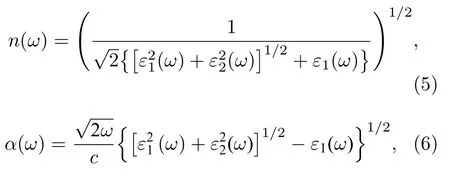
图4(a)表示各体系介电常数实部ε1(ω),实部越大,对电荷的束缚能力越强,表明材料的极性越强.从图4(a)可看出,未掺杂和各掺杂体系的静态介电常数ε1(0) 分别为7.106,23.330,9.483 和6.001.当ε1(ω)>0时,光子通过材料传播,当ε1(ω)<0 时,电磁波衰减,当ε1(ω)0 时,产生纵向极化波.所有体系在4—8.5 eV 范围内都存在负值,表明在此处存在能量间隔,会使得电磁波的传播过程衰弱[42].图4(b)表示各体系介电常数虚部ε2(ω),虚部越大,电子吸收光子的可能性越大,激发态的电子数越多,跃迁的概率就越大.从图4(b)可以看出,所有掺杂体系的攀升点相对于未掺杂WS2体系移向低能区,表明电子更容易跃迁.此外,在光子能量约2.5 eV 处存在一组由带间跃迁形成的尖锐峰.对于未掺杂WS2体系,此峰主要由S 原子p 价带向W 原子d 导带跃迁形成的[42,43].图4(c)显示了与ε1(ω)有类似趋势的折射系数n(ω),可以看出,低能区域中Mn 掺杂体系的峰值高于Tc,Re 掺杂体系,而在高能区域逐渐倾向于重合,这表明Mn 掺杂体系对长波光具有较强的折射,而未掺杂WS2体系对长波光具有最强的折射,并且在短波区域中所有体系的差异逐渐消失.图4(d)表示各体系的吸收系数α(ω),吸收系数的损耗和增益与ε2(ω) 密切相关,WS2掺杂后以很小的能量激发光电子从而产生吸收.从图4(d)可以看出,Mn,Tc,Re 掺杂WS2的体系均发生了红移,并且Mn 掺杂体系最为明显,还可看出在低能区域Mn 掺杂体系的α(ω) 最大,这表明引入掺杂以后对WS2体系的吸收系数有显著的影响.

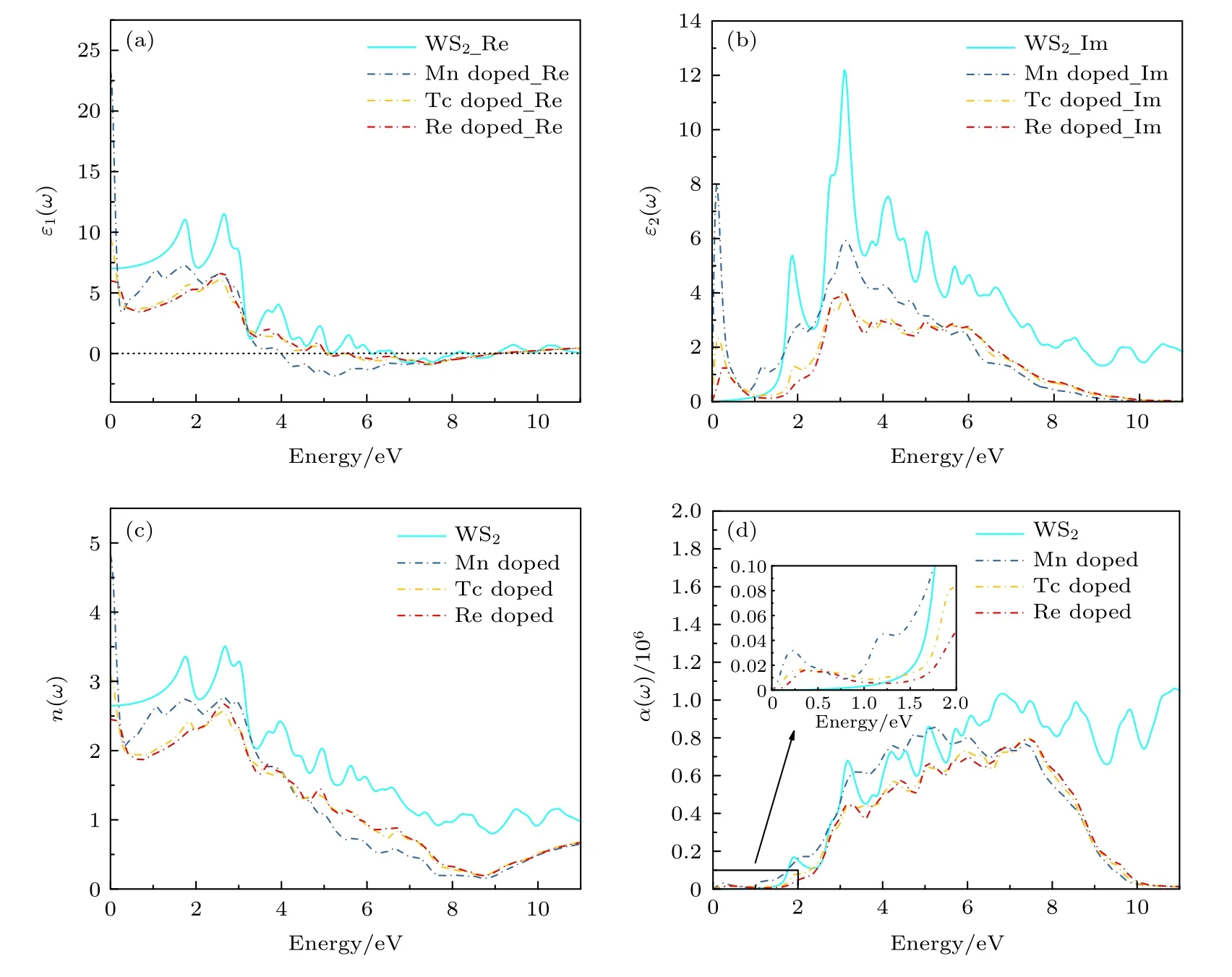
图4 未掺杂与掺杂二维WS2 的光学性质 (a) 介电函数实部 ε1(ω);(b) 介电函数虚部 ε2(ω);(c) 折射系数 n(ω);(d) 吸收系数α(ω)Fig.4.Optical properties of undoped and doped two-dimensional WS2:(a) The real part of the dielectric constant ε1(ω);(b) the imaginary part of the dielectric constant ε2(ω);(c) the refractive index n(ω);(d) absorption coefficient α(ω).

4 结论

本文采用基于密度泛函理论的第一性原理投影缀加平面波方法研究ⅦB 族过渡金属原子X(X=Mn,Tc,Re) 掺杂二维WS2体系的电子结构、磁性和光学性质.结果表明:掺杂体系在S-rich 条件下比在W-rich 条件下更稳定,且Tc 掺杂的WS2体系在S-rich 条件下具有最小的形成能–1.292 eV.Mn 掺杂体系中两个自旋子能带分别具有不同的导电特性,整体呈现磁矩为1.001 μB的半金属铁磁性,其独特的电子结构是设计高效自旋电子器件的理想材料,具有重要的学术意义和潜在的应用价值.在Tc 与Re 掺杂体系中,费米能级EF同时穿过完全一致的自旋向上和自旋向下通道中导带底的杂质带,体系为非磁性N 型半导体,可用于设计场效应晶体管、发光二极管和光电探测器等光电器件.在Mn 掺杂体系中,自旋向上与自旋向下态密度不对称,证明体系存在磁性,而在Tc 与Re 掺杂体系中,自旋向上与自旋向下态密度相互对称,证明体系没有磁性.从Mn 到Re 掺杂的WS2系统,由于Mn,Tc,Re 磁性的差异,EF附近杂质态的自旋分裂程度依次减小,这导致体系从半金属铁磁特性过渡到非磁性N 型半导体特性.掺杂前后WS2体系均有着优良的光学性质,在低能量区域介电常数和折射系数与未掺杂WS2的体系相比明显增强,掺杂体系在远红外范围内的吸收系数增强且发生红移,峰值增大,在远红外探测器中具有潜在的应用价值.