低维超导材料中的量子振荡现象*
2022-07-19毕翔宇黄俊伟秦峰邱彩玉袁洪涛
毕翔宇 黄俊伟 秦峰 邱彩玉 袁洪涛
(固体微结构物理国家重点实验室,南京大学现代工程与应用科学学院,南京大学人工微结构科学与技术协同创新中心,南京 210000)
低维超导材料由于具有尺度接近量子临界尺寸的优势,能够观测到显著的超导量子振荡效应,因此成为研究超导量子振荡效应的优异平台.由于这些量子振荡效应的周期、振幅、相位与磁通涡旋的量子化及运动方式、超导电子的配对机制、特定外部条件下超导体中的涨落和激发现象密切相关,并且它们还能直观地反映超导材料的几何结构对其超导物性的影响,因此对低维超导体中振荡效应的研究直接反映了超导体的本质规律,成为研究材料超导机制的一种重要手段,有着深邃的物理内涵和丰富的研究价值.本文将探讨三类能够在低维超导材料中观测到的典型超导量子振荡效应:利特尔-帕克斯效应、磁通涡旋运动导致的振荡效应和韦伯阻塞效应,从研究手段、理论预期、实验现象以及实验结果诸方面综述其中所揭示的深刻物理规律,并展望低维超导体的量子振荡效应在量子计算、器件物理和低温物理等领域的应用价值.
1 引言
超导电性是指在临界温度以下体系的电阻突变为零的奇异物理现象.具有超导电性的材料是探索凝聚态体系电子间复杂的多体相互作用的范本[1,2],并且超导相在外界条件下的不同演化行为也是研究凝聚态体系中有序与涨落的典例[3−5],因此对材料超导电性的研究始终是当代物理学的前沿.随着近些年来材料制备手段的长足进步,超导纳米薄膜、纳米线、纳米管等二维乃至准一维的新兴低维超导材料不断被发现[6−17].超导维度的降低为超导现象的研究注入了新的活力,因此深入理解二维、甚至准一维超导体的基本物性,尤其是相关的量子现象显得愈发重要,如莫尔超晶格(moiré superlattice)中的超导行为[6,7]、量子格里菲斯奇异性(quantum Griffith singularity)[8−10]、非超导材料界面上的二维超导电子气[11−13]等.其中代表性的低维超导材料体系包括LaAlO3/SrTiO3界面[11,12]、离子液调制的MoS2表面[13]、原子级NbSe2薄层[14,15]、转角双层/三层石墨烯[6,7]、超导纳米管[16,17]等.
当材料的线度达到与其晶格尺寸可比拟的纳米尺度时,包括超导电性在内的物理特性与对应的块材相比往往会有显著的区别.以金属铝为例,块材铝属于典型的第一类超导体,在超导态下内部无磁通;当减薄为纳米级厚度的二维超导铝薄膜时,该材料会转变为第二类超导体,即在该情况下外磁场能够以磁通线(flux line)的形式进入超导态的材料内部[18,19];当对超薄铝膜的宽度再施加限制使之成为一维的超导纳米线时,在该体系中就会呈现出“韦伯阻塞”(Weber blockade)这一独特的量子振荡现象[20].由此可见,超导体维度的变化会对其基本物性产生深远的影响.有鉴于此,研究低维超导体中的新现象、新机制,以及调控低维超导电性的新手段、新方法逐渐成为低维超导材料实用化的当务之急.
由于受制于量子限制效应,且比表面积大、界面效应显著,低维超导体在研究超导量子现象上有着传统体相材料所无法比拟的巨大优势,主要体现在:1)低维超导体是研究多种多样的超导配对机制的优越平台,包括BCS-BEC 过渡(Bardeen-Cooper-Schrieffer-Bose-Einstein condensation crossover)理论[21,22]、二维超导体系中的BKT 相变(Berezinskii-Kosterlitz-Thouless transition)理 论[4,5,23]、一维超导体系的LAMH(Langer-Ambegaokar-Mc-Cumber-Halperin)理论[24−26]、以及伊辛配对机制(Ising pairing mechanism)[14,27−29]、自旋三重态(spin-triplet)配对[30−32]、d 波超导配对等[33−35],也是探索高温超导机制的重要平台[36−39];2)低维超导体可以用于直观地分析磁通涡旋的量子化及其钉扎效应和运动规律[1,2,40−43],包括本文将要着重探讨的利特尔-帕克斯振荡(Little-Parks oscillation)[17,44−47]、磁通涡旋运动导致的振荡[48−50]以及韦伯阻塞效应等[18,20,51−53];3)不同的低维薄膜之间可以形成范德瓦耳斯异质结[54−56],能够通过扭转、堆叠等对称性工程手段调控其物性(如转角双层石墨烯超导电性的研究[6,57]),也可以通过将具有不同物性的薄膜堆叠在一起来研究界面的新颖物性(如超导/铁磁异质界面的研究[58−60]).
超导体中的量子振荡现象通常与量子化磁通的进入和运动密切相关[1−3,61].在施加外磁场的过程中,磁场会以磁通线的形式进入到第二类超导体之中并产生磁通涡旋.在磁通涡旋的核芯(即半径小于相干长度的部分,或称磁通芯子)呈现正常态,超导电子无法在其中流动.超导体中磁通涡旋对应的量子化磁通Φ0h/(2e)2.07×105Wb,其中h为普朗克常量,e代表元电荷,分母中的系数2 是超导体中电子两两配对形成库珀对(Cooper pair)所导致的结果[62].有趣的是,在低维度的第二类超导材料中,由于磁场垂直样品平面方向的穿透深度λ往往大于材料厚度d,超导体中的磁通涡旋属于Pearl 类型[63],在实空间呈现出圆盘状,并能够排列成有规律的阵列.当外部条件(如施加的磁场强度、电流密度或体系温度)发生改变时,磁通涡旋会不断运动,并且其排列方式也会随之改变,从而导致了超导量子振荡效应的产生[1,2].通过对这些低维超导体中丰富的量子振荡现象的分析还可以获得很多新的物理规律(如表1 所列),因此研究低维超导体中的量子振荡现象在理论和应用上都有着巨大价值[44−53,64,65].

表1 低维超导体的超导量子振荡现象Table 1. Superconducting quantum oscillation phenomena in low-dimensional superconductors.
虽然介绍超导体各种新颖性质的综述文章层出不穷,但对超导量子振荡现象的总结却鲜见报道.因此本文将重点介绍1)利特尔-帕克斯振荡、2)外场激发的磁通涡旋运动(vortex motion)所导致的振荡、3)韦伯阻塞这三类低维超导体中存在的典型超导量子振荡效应,与这些现象密切相关的研究进展,以及通过对这些振荡效应的观察和分析所提炼出的新规律,包括对自旋三重态配对的超导现象的研究[66]、外部条件引发的涨落效应对磁通涡旋运动影响的探索[49,50]、超导-绝缘体转变中玻色金属态的证实等[39].本文的逻辑结构和选取的典型实例如图1 所示.
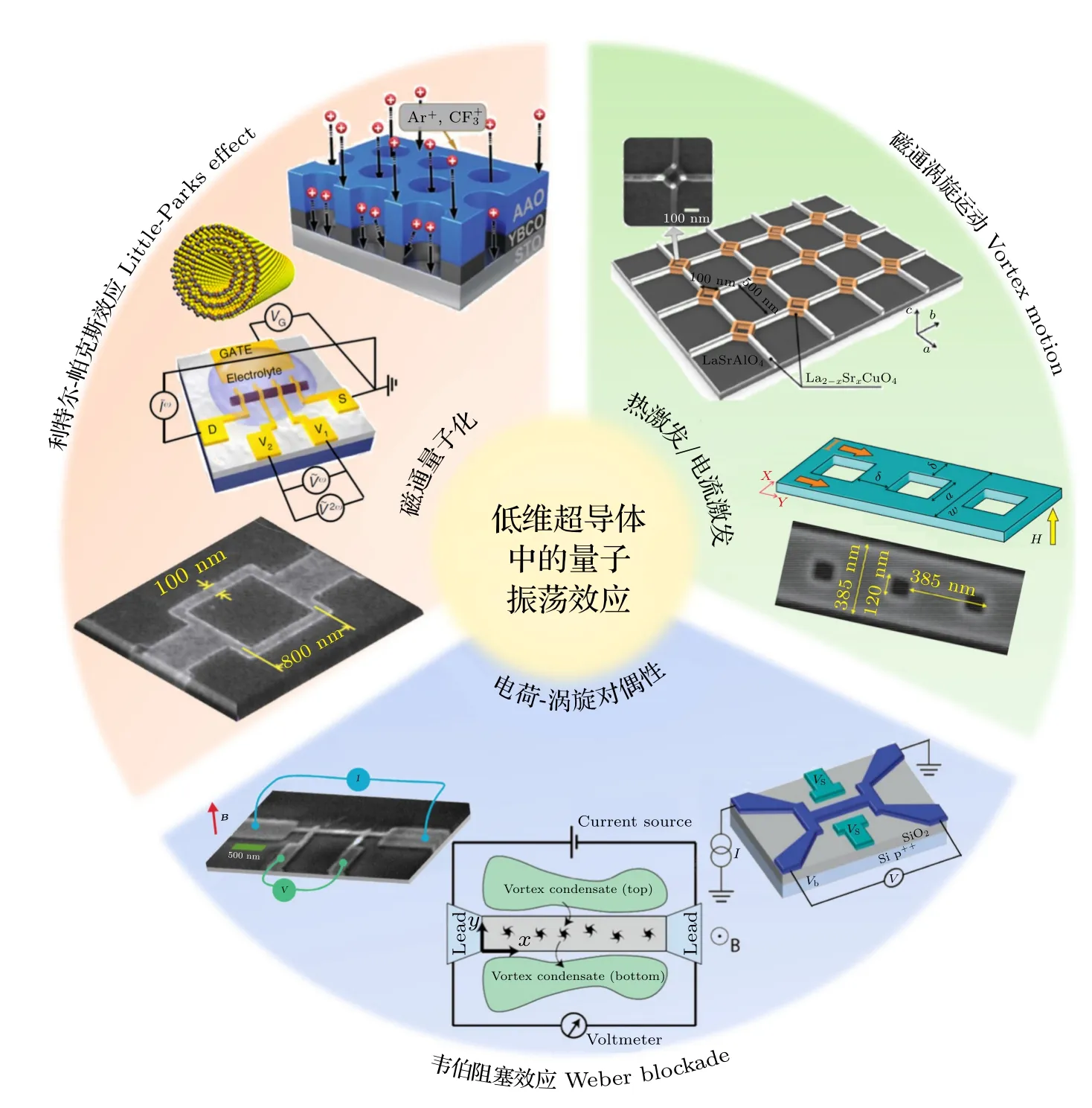
图1 低维超导体的超导量子振荡效应分类(利特尔-帕克斯效应、磁通涡旋运动、韦伯阻塞效应)与对应的物理机制,以及一些典型实例[17,20,39,49−51,53,66]Fig.1.Superconducting quantum oscillation effects observed in low-dimensional superconductors.Three distinct effects,including the Little-Parks (LP) effect,vortex motion effect and Weber blockade effects,together with the physical mechanisms and typical experimental results,are presented [17,20,39,49−51,53,66].
2 利特尔-帕克斯振荡
利特尔-帕克斯效应是超导体中最典型、研究最广泛的超导量子振荡效应之一,也是超导体中磁通量子化的一个最直接的实验证据.该效应是指在温度T略低于超导临界温度TC时,对于厚度小于穿透深度λ或与之可比拟的超导样品之中存在一个或多个孔洞(即复连通的超导材料),随着外加磁场的增大,材料的电阻呈现周期性振荡的现象[44,45].由于磁通的量子化与材料中的载流子形式、超导电子的配对机制等密切相关,因此对超导体的利特尔-帕克斯效应的研究有着重要的意义.
2.1 物理机制
在复连通的超导体中,自由能呈现出随外磁场的非单调响应关系,表现为利特尔-帕克斯效应.在连续变化的磁场中,超导体所俘获的量子化的类磁通(fluxoid)的个数只能取整数,导致超导电子的动能随外磁场的增加而呈现周期性变化,且其变化周期等于一个额外的磁通线进入材料体系时磁场的变化量.另一方面,正常金属态的自由能与外磁场之间并没有上述关系,因此超导态与金属态的自由能之差也随着外加磁场强度的改变而周期性变化,最终表现为超导体的超导临界温度TC随着外磁场变化而周期性变化.这就是利特尔-帕克斯效应的物理机制,可以理解为超导库珀对[62]的阿哈罗诺夫-玻姆效应(Aharonov-Bohm effect)[67,68].
为了研究利特尔-帕克斯效应,研究者们往往会设计两类实验方法来解析其振荡周期和幅值等重要参量.第一类实验方法:测量超导临界温度TC随外磁场变化的周期性改变,通常通过在不同磁场下扫描一系列电阻-温度曲线来得到[46],如图2(a)所示.这种方法是最为直接的观测手段,但是要求具有极高的临界温度的测定精度,比较难以实现.第二类实验方法:固定体系所处的温度,以足够小的步长扫描磁场,记录体系电阻随外磁场的变化[17],如图2(b)所示.相对而言,第二类方法所需的温度控制高稳定性和磁场扫描精细步长的实验条件容易实现,因此是观测利特尔-帕克斯效应更常用的手段[39,47,66].对于第二类实验方法,由于利特尔-帕克斯效应直观反映的是临界温度的振荡,因此特定温度下的磁电阻振荡幅度正比于该温度下的电阻-温度曲线变化率 dR/dT[1,44,45,69].特别地,由于材料在超导转变温度附近的 dR/dT值最大,磁电阻的振荡效应也最明显,因此一般在超导转变的温度区间内分析磁电阻信号的利特尔-帕克斯振荡.需要指出的是,从图2 还可以看出,使用这两类实验方法所测出的实际曲线都会耦合背景信号(即无振荡的超导转变信号),只有消除背景信号才能更好地观测周期性振荡结果.比如,测定的电阻-磁场曲线包含U 形的背景信号(图2(b)),可以通过偶次多项式拟合的方法将之扣除[17].另外,背景信号的存在也导致利特尔-帕克斯振荡的振幅随磁场绝对值的增大而减小,所以实验中只有在磁场较低的范围内才能够观测到明显的振荡现象[17,44,45].
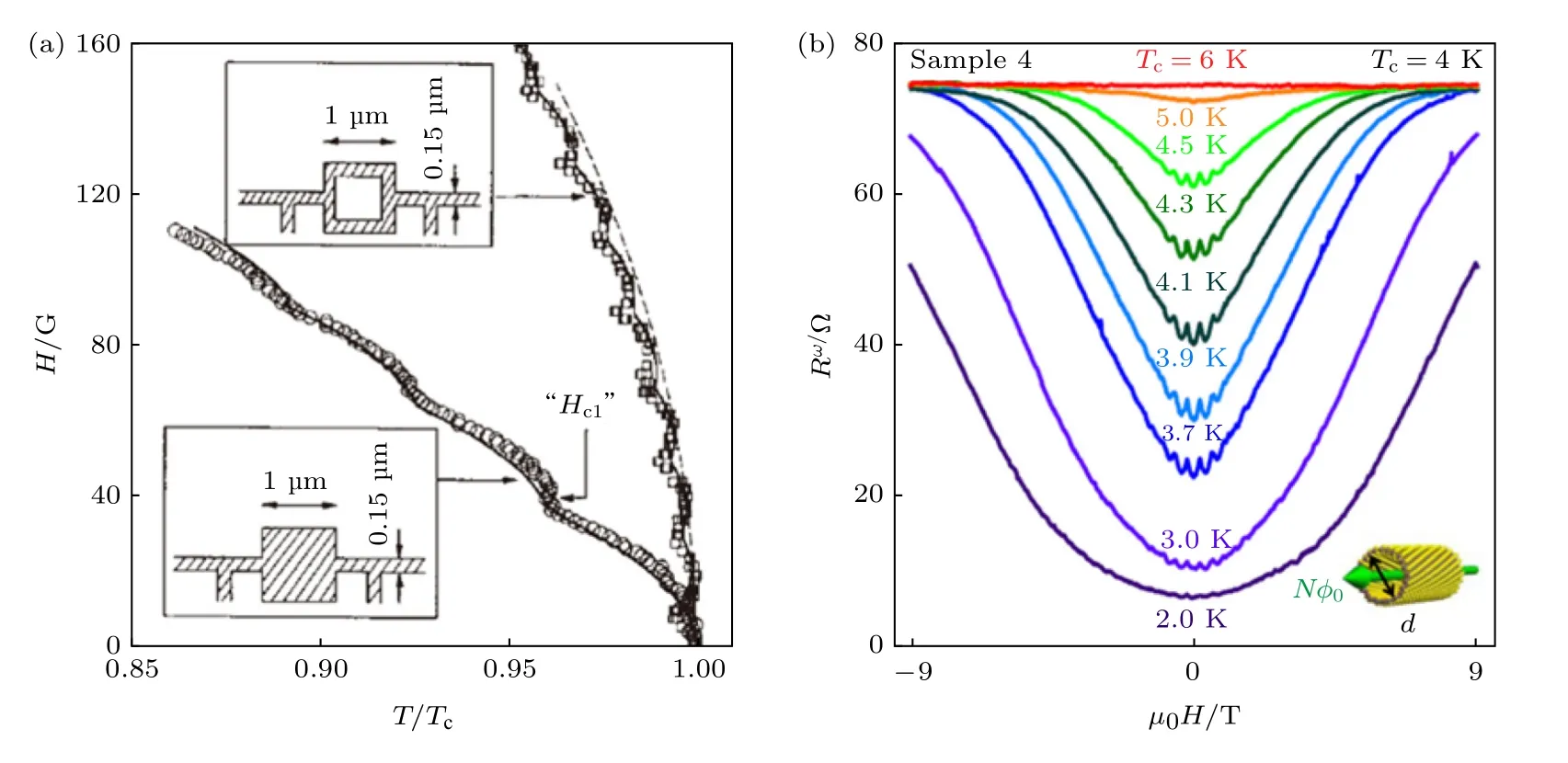
图2 利特尔-帕克斯效应的实验观测方法 (a) 通过磁场-临界温度关系的实验观测方法,其中外磁场垂直于样品平面,且临界温度对零磁场下的临界温度作了归一化处理,样品为超导铝纳米结构,形状及尺寸如内置插图所示[46];(b) 通过电阻-磁场关系的实验观测方法,样品为超导WS2 手性纳米管,外磁场方向沿管径向,如右下角示意图所示.通过振荡周期推算出的纳米管有效直径 d80 nm,这与透射电子显微镜的表征结果相符[17]Fig.2.Experimental observation of LP effect:(a) By determining the relation between the superconducting critical temperature and the applied magnetic field,the LP oscillation can be observed in the H-TC relation.The sample used for the observation is a superconducting Al nanostructure,whose shape and size are presented in the inset figure.Note that the applied magnetic field is perpendicular to the sample surface,and that the superconducting critical temperature has been normalized by the critical temperature under zero magnetic field[46].(b) By determining the relation between the four-terminal resistance and the applied magnetic field,the LP oscillation can be found in the R-T relation near a zero magnetic field.The sample used for the observation is superconducting chiral nanotube WS2,and the orientation of the applied magnetic field is along the nanotube axis.The calculated effective diameter of the superconducting nanotube is d80 nm based on the periodicity of the oscillation,which is consistent with the pictures taken by transmission electron microscope[17].
除此之外,基于d 波配对的高温超导理论指出,高温超导体应当表现为周期h/e的振荡[70−72],一些高温超导纳米线的振荡周期还被认为是半个量子化磁通h/(4e)[73],有些理论还预测自旋三态(spin-triplet)的超导体在零磁通状态下对应的TC并非极大值而是极小值[74]等.这些都为超导体的利特尔-帕克斯效应研究注入了新的活力.
2.2 研究近况
如上所述,利特尔-帕克斯效应的物理机制相对明晰,通过研究振荡的周期、振幅、相位等特征都有助于发现新现象和新规律.比如,在自旋三重态配对的拓扑超导体中对半整数利特尔-帕克斯效应的研究[66,75]、在超导纳米管中通过利特尔-帕克斯振荡分析其临界维度随有效管径的变化规律等[17,47].此外,利特尔-帕克斯效应的振荡周期直接反映了材料中载流子两两配对的存在形态,对该效应的研究可以用于探讨和分析新物态,比如对二维体系绝缘体-超导相变中反常金属态特性的研究等[39].下文将分别介绍该方向的几类典型工作,包括:1)自旋三重态配对的超导体β–Bi2Pd、自旋三重态与自旋单态混合配对超导体α–BiPd 中的利特尔-帕克斯振荡效应;2)手性多壁WS2纳米管中的利特尔-帕克斯效应;3)利用利特尔-帕克斯效应研究高温超导体钇钡铜氧(YBa2Cu3O7–x,YBCO)的超导-绝缘体相变过程中的反常金属态等.
2.2.1 自旋三重态超导体β–Bi2Pd 中的利特尔-帕克斯振荡效应
利特尔-帕克斯振荡的周期和振幅,以及零磁通状态下自由能极值的类型(极大值/极小值)被认为与材料体系的类型和电子配对方式等有关.尤其是高温超导体、拓扑超导体等热门研究对象中的利特尔-帕克斯振荡的特征很有可能与传统BCS超导体迥乎不同[69−73,76].为了验证上述理论预测,约翰斯·霍普金斯大学的 Chien 课题组[66]通过对多晶态拓扑超导体β–Bi2Pd 中的利特尔-帕克斯振荡效应进行了研究,并将研究结果与相同几何结构的常规超导体Nb 的振荡进行对比,观测到了两种材料的利特尔-帕克斯振荡曲线之间存在的 π 相位差异,并据此证实了β–Bi2Pd 超导体中的自旋三重态配对机制.
为了直观反映自旋三态配对的β–Bi2Pd 超导体与以Nb 为代表的常规BCS 超导体之间的差异,Chien 课题组对比了两种材料的利特尔-帕克斯效应,如图3 所示[66].其中,图3(a)和图3(b)分别给出了s 波配对的常规超导体和自旋三态超导体的临界温度和磁电阻的利特尔-帕克斯振荡的示意图.二者的振荡周期虽然都对应于一个磁通量子Φ0,但相位却存在明显的差异:常规超导体的TC极大值(磁电阻极小值)对应于Φ′nΦ0,而多晶结构的自旋三态超导体却对应于Φ′(n+1/2)Φ0,其中n为整数[74].实验结果表明,Nb 磁电阻信号的利特尔-帕克斯振荡曲线(图3(c))与常规超导体的振荡行为(图3(a))很好地相符,而多晶β–Bi2Pd的利特尔-帕克斯振荡结果(图3(d))却明显与自旋三态超导体的振荡特征(图3(b))相吻合.上述结果并不随着磁场扫描速率和外加电流强度的变化而变化,并且在超导转变温度区间内都能够观测到相同的结果.该工作通过不同配对机制超导体中利特尔-帕克斯振荡效应的实验对比,成功在β–Bi2Pd体系中证实了其自旋三重态配对的物理机制,不仅从实验上给出了超导体自旋配对情况的一种判断方法,还证实了由自旋三重态超导体构成的介观超导环应用于超导量子比特(superconducting qubits)的巨大价值[66,77].

图3 常规超导体(s 波配对)与自旋三重态超导配对机制对应的利特尔-帕克斯效应对比[66] (a) 常规超导体的温度(上图)、磁电阻(下图)随磁场变化的利特尔-帕克斯振荡示意图,零磁通状态对应于临界温度 TC的极大值、磁电阻 R 的极小值;(b) 自旋三重态配对的超导体的温度(上图)、磁电阻(下图)随磁场变化的利特尔-帕克斯振荡示意图,零磁通状态对应于 TC的极小值和R的极大值,与(a)刚好相反;(c) 常规超导体Nb 磁电阻的利特尔-帕克斯振荡效应,与图(a)相符,其中磁场强度对30.2 Oe (单个磁通线对应的磁场强度,1 Oe=103/(4π) A/m)进行了归一化处理;(d) 拓扑超导体β-Bi2Pd 磁电阻的利特尔-帕克斯振荡,上图为原始曲线,下图为去掉多项式背景信号后的曲线,其振荡现象与图(b)相符,证实了其自旋三重态配对的物理机制Fig.3.Comparison of the LP oscillation effect between conventional superconductor (s-wave pairing) and spin-triplet superconductor[66]:(a) Schematic diagram of the LP effect of a conventional superconductor reflected by the critical temperature (upper panel) and magnetoresistance (lower panel).Note that the zero magnetic field state is associated with the maximum of TC and the minimum of R.(b) Schematic diagram of the LP effect of a spin-triplet superconductor reflected by critical temperature (upper panel) and magnetoresistance (lower panel).Herein,the zero magnetic field state is associated with the minimum of TC and the maximum of R,which is directly opposed to (a).(c) LP oscillation observed from magnetoresistance for conventional superconductor Nb,which is in accordance with the lower panel of (a).The magnetic field is normalized by 30.2 Oe,which is associated with a single magnetic fluxoid quantum.(d) LP oscillation of topological superconductor β-Bi2Pd observed from magnetoresistance.The upper panel shows the original data,and the lower panel shows the signal of oscillation by subtracting the normal R-H relation.The LP oscillation is in good accordance with the lower panel of (b),directly confirming the nature of the spin-triplet pairing mechanism of β-Bi2Pd.
2.2.2 自旋单态与自旋三重态共存的α–BiPd中的利特尔-帕克斯振荡效应
在前文对自旋三重态配对超导体的利特尔-帕克斯效应研究基础上,约翰斯·霍普金斯大学的Chien 课题组[75]进一步设计实验,希望通过利特尔-帕克斯效应证实一些特殊超导体中自旋单态与自旋三重态配对机制共存的现象.对于中心反演对称的超导体而言,其对称性的制约导致其超导电子的配对只能是完全具有偶宇称的自旋单态,或完全具有奇宇称的自旋三重态[78].但是,中心反演对称性破缺的超导体则不受此限制,可以表现为自旋单态/三重态混合的配对方式[79].单斜结构的α–BiPd就属于这种中心反演对称性破缺的超导体.但是,以往对于该超导体的实验结果表明其配对形式以自旋单态的s 波超导为主导[80],而上述单态/三重态混合的配对机制始终缺乏直接的实验证据.这里,研究者们利用观测到的利特尔-帕克斯效应振荡的相位依赖性的统计结果成功证实了上述两种配对机制的共存[75].在该实验中,50 nm 厚的多晶α-BiPd 通过磁控溅射方法沉积到SrTiO3的(001)面上,其超导转变温度为3.6 K.进一步地,Chien课题组利用电子束刻蚀技术将样品制成亚微米尺度的方形超导环,并在不同温度的磁电阻信号之中都观察到了极大值位于Φ′(n+1/2)Φ0的半整数利特尔-帕克斯效应(图4(a)),该信号与磁场的扫描方向无关,并在其他尺寸的器件中都能够被观察到,证实了α–BiPd 中自旋三重态配对机制的存在.
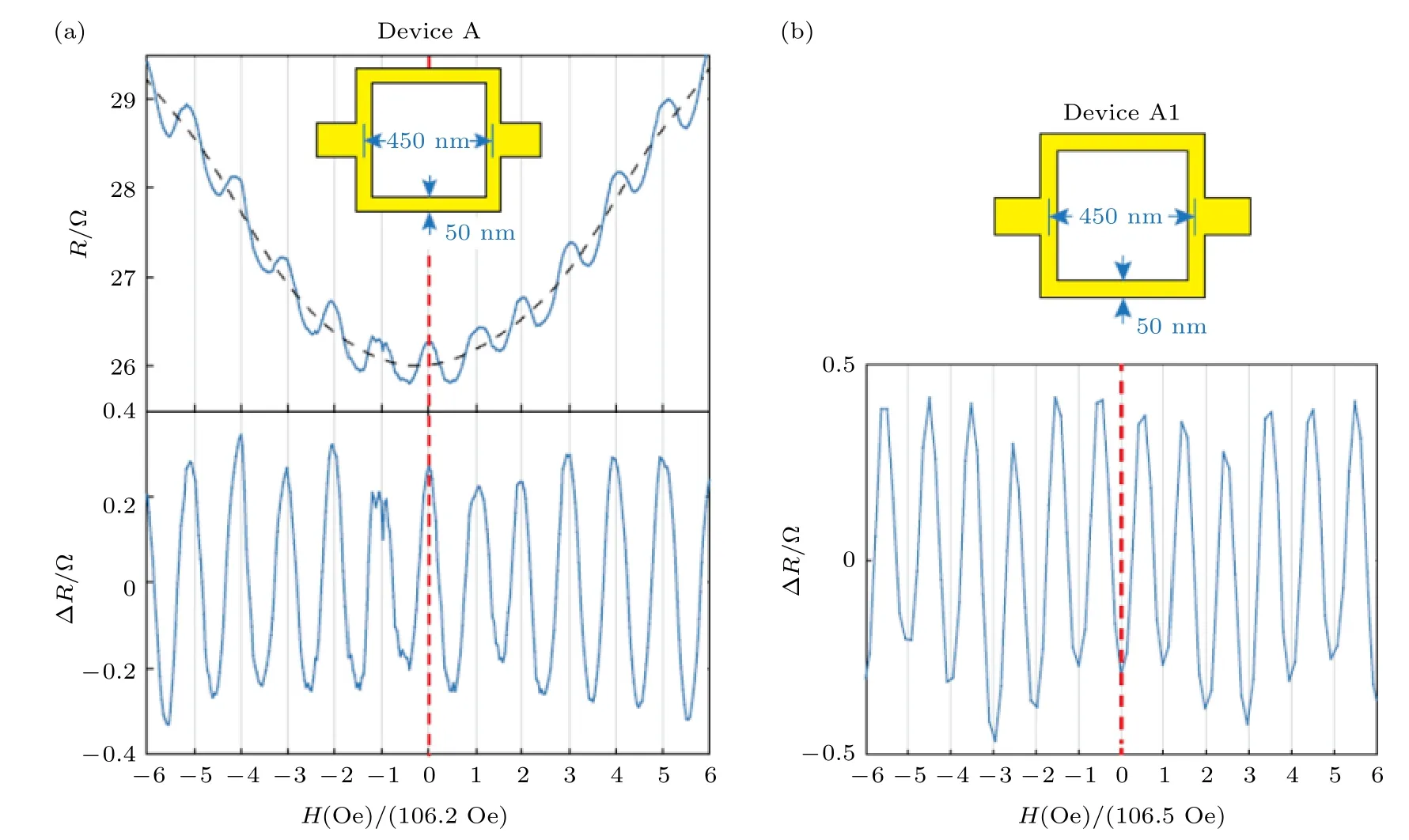
图4 对 α–BiPd 超导环的利特尔-帕克斯振荡的分析[75] (a)零磁通对应于磁电阻极大的利特尔-帕克斯振荡原始曲线(上图,标记为 R)及去掉多项式背景后的结果(下图,标记为 ∆R),该振荡的行为与图3(b)相对应,这样的超导环被称为“ π ”环;(b)零磁通对应于磁电阻极小的利特尔-帕克斯振荡,这里直接展示的是去掉背景后的结果(标记为 ∆R),与图3(a)相对应,这样的超导环被称为“0”环Fig.4.Analysis of LP oscillation for the α–BiPd superconducting ring[75]:(a) LP effect where the maximum resistance corresponds to the zero magnetic flux.The upper panel shows the original data of R-Hrelation (the resistance is marked as“ R ”,and the sample size is shown in the inset panel),and the lower panel shows the results after subtracting the normal magnetoresistance data(marked as“ ∆R ”).The characteristics of the oscillation corresponds to Fig.3(b),and this kind of superconducting ring is named the“ π ”ring.(b) LP effect where the minimum of resistance corresponds to zero magnetic flux.The characteristics of the oscillation correspond to Fig.3(a),and this kind of superconducting ring is named the“ 0 ”ring.
理论分析指出,多晶的自旋三重态超导体的利特尔-帕克斯效应观测到的磁电阻极小值对应于Φ′nΦ0(简称为“0”环,对应于图3(a))和Φ′(n+1/2)Φ0(简称为“ π ”环,对应于图3(b))两种情况是等概率的,而自旋单态超导体则只能观测到“0”环[66].对上文中提到的自旋三重态超导体β–Bi2Pd 的统计结果为,在21 个器件中观测到了约60%的“ π ”环,与预测相符.而对非中心对称的超导体而言,观测到“ π ”环的概率应该处于0(完全自旋单态配对)和50%(完全自旋三重态配对)之间.研究者们在共计16 个α–BiPd 超导器件中观测到了3 个“ π ”环(概率小于20%)和13 个“0”环(典型实验结果如图4(b)所示),不仅说明了该材料中自旋单态和三重态配对方式的共存,还进一步验证了这两种配对机制中以自旋单态配对为主导.
2.2.3 手性多壁WS2纳米管中的利特尔-帕克斯振荡效应
除了通过利特尔-帕克斯效应验证超导体中电子的配对机制外,还可以通过该振荡的周期对超导材料的一些几何参数进行计算,以此为“跳板”对其他物理问题进行研究.东京大学的Iwasa 课题组[17,47]对KClO4液体电解质调制的手性多壁WS2纳米管的超导电性研究就是典型的例子.为了研究超导纳米管临界温度的管径依赖关系,研究者们需要确定已知临界温度的纳米管的准确管径数值,于是就利用超导纳米管中存在的利特尔-帕克斯振荡的周期反推出管径数值,从而在实验上成功给出了TC与管径之间的关系,填补了相关研究空白.WS2材料属于过渡金属硫属化合物(transition metal dichalcogenides,TMDCs)的一种,本征的WS2纳米管属于半导体,但在外加栅极电压调制下,K+离子通过电化学作用被掺入样品之中,使体系呈现超导电性[17,81].为了进一步研究纳米管超导转变温度TC随纳米管径的变化规律,研究者们严格控制外磁场方向沿纳米管径向,并测试沿该方向的磁电阻信号,通过分析磁电阻的利特尔-帕克斯振荡周期,结合公式µ0∆H ·πD2/4Φ0来确定纳米管的有效管径(其中µ0代表真空磁导率,∆H代表磁电阻关于磁场的振荡周期,D为纳米管的管径数值).
研究结果表明,上述离子液调制的纳米管的超导转变温度与管径呈正相关,更定量的分析还表明TC与管径的倒数(即纳米管的曲率)呈线性关系(图5)[47].研究者们还对比了KClO4液体电解质调制的WS2薄膜(可以视为管径趋于无穷的超导纳米管)的超导转变温度的实验结果[82],该结果也与实验关系的外推曲线相吻合,说明了实验规律的可靠性.最后,研究者们还通过进一步的分析排除了钾离子掺杂浓度和管壁厚度两个因素对TC的影响,说明了在该实验条件下TC只受到管径这一个变量的影响[47].然而,此前基于电声耦合超导机制的理论分析给出了与实验完全相反的预测[83],这说明目前对纳米管中电声散射机制的理解仍然不够明晰.总之,上述实验结果以对利特尔-帕克斯效应的分析为桥梁,为研究超导纳米管中存在的物理机制提供了重要的实验基础.

图5 对手性超导WS2 纳米管的临界温度与管径间的关系研究[47] (a) 管径不同的4 根超导纳米管的利特尔-帕克斯振荡以及根据公式 µ0∆H ·πD2/4Φ0计算出的管径D 和超导临界温度 TC (标在每条曲线上方);(b) 4 根WS2 超导纳米管以及WS2 薄膜的电阻-温度关系,其中电阻值对正常态的电阻作了归一化处理;(c) 4 根WS2 超导纳米管以及WS2 薄膜的超导临界温度-管径关系,其中WS2 薄膜的管径被认为是无穷大Fig.5.Investigation of the relation between the diameter of superconducting chiral WS2 nanotubes and the critical temperature[47]:(a) LP oscillation for 4 superconducting nanotubes with different diameters (D).The values of D are obtained based on the formulaµ0∆H ·πD2/4Φ0and the corresponding TCof each nanotube is marked on top of each curve.(b) The R-H relations for 4 superconducting nanotubes (corresponding to the order number in (a)) and superconducting WS2 flakes.(c) The relation between superconducting critical temperatures and diameters of nanotubes,where the diameter for WS2 flake is considered to be infinite.
2.2.4 钇钡铜氧纳米多孔薄膜中的利特尔-帕克斯振荡效应
除了上文将利特尔-帕克斯效应应用到超导态样品的研究之外,对利特尔-帕克斯效应的研究方法还可以迁移到对新物相的基本特性的分析之中.二维超导体的绝缘体-超导相变是凝聚态物理学的一个前沿领域,尤其是对该相变过程中反常金属态的存在与否在过去的几十年间始终有着较大的争议[84,85].2019 年,电子科技大学熊杰课题组、北京大学王健课题组和布朗大学Valles 课题组[39]共同通过对多孔氧化铝模板上的YBCO 超导体纳米多孔薄膜(结构见图6(a))的输运性质分析,在不同的RIE 刻蚀条件下使材料依次呈现出超导(superconducting,SC)-反常金属(anomalous metal,AM)-过渡态(transitional state,TS)-绝缘态(insulating state,INS)的4 种典型电阻-温度曲线(如图6(b)所示),还测试了外加垂直磁场下的磁电阻信号并分析其振荡周期,最终证实了二维反常金属态的存在.其中,为了确定这种反常金属态的基本物性,尤其是其中电子的行为,研究者们对该物相的利特尔-帕克斯振荡的周期进行了分析.

图6 对二维超导体的绝缘体-超导相变中反常金属态的研究[39] (a) 样品结构示意图,样品由无定形氧化铝(标记为AAO)、钇钡铜氧超导体(标记为YBCO)和钛酸锶衬底(标记为STO)三层结构构成,多孔结构是利用Ar+和 离子刻蚀的结果;(b) 不同刻蚀时间下得到的SC,AM1,TS 以及INS 对应的4 种典型电阻-温度关系;(c)—(e) 不同温度下超导态(c)、反常金属态(d)、绝缘态(e)的归一化电导变化量随外磁场的振荡关系,这3 种态对应的振荡表现出了相同的周期;(f) 超导态、反常金属态、绝缘态的磁电导振荡幅度与温度的关系Fig.6.Investigation of anomalous metal state existing in the transition from insulator to superconductor[39]:(a) Schematic illustration of the sample structure,including the amorphous alumina (AAO),Y-Ba-Cu-O superconductor (YBCO) and SrTiO3 (STO) layers.The porous structure is obtained by ionic etching of Ar+ and ,respectively.(b) The R-T relations for 4 typical states:SC,AM1,TS and INS.(c)–(e) The oscillation signals in the R-H relations observed from normalized electrical conductance for the superconducting state (c),anomalous metal state (d),and insulating state (e).Note that the abovementioned three states have identical periodicity.(f) Temperature dependence of the oscillation amplitude for the abovementioned three states.
得到反常金属态存在的证据后,研究者分别研究了超导态(图6(c))、新发现的反常金属态(图6(d)),以及绝缘态(图6(e))的样品中电阻与磁场的关系.研究表明三者的电阻都随磁场强度的变化呈现出以Φ0h/(2e) 为周期的量子振荡.其中,超导态呈现出这样的振荡不难理解(利特尔-帕克斯效应的典型体现),但反常金属态仍然呈现出这样的振荡周期则十分新颖.对于传统的金属而言,无论是采用特鲁德模型(Drude model)还是自由电子气模型来描述,载流子都是单个电子,那么其中的磁通量子应当对应于h/e,即磁场变化时,样品的振荡周期应当为h/e而非实验观测到的h/(2e).该现象说明反常金属态中的电子同样是以电子对的形式来运动.换句话说,可以认为反常金属态的载流子为玻色子,因此也被称为“玻色金属态”(bosonic metallic state)[86],这与传统的金属有着显著的区别.
另外,更加深入的分析表明,与超导态样品利特尔-帕克斯振荡幅度随温度降低而迅速发散不同,反常金属态中的振荡幅度随温度降低而趋于一个饱和值,绝缘态的振幅则随温度的降低先增大后减小(图6(f)).这些现象都不适合用基于固体能带论的传统金属理论来解释,通过对其深入分析有望对相变过程中存在的反常金属态的物理本质进行更好的理解[39].
由此可见,利特尔-帕克斯振荡效应不仅广泛地存在于多种配对类型、多种维度的超导体之中,直观反映不同配对机制的差异及其共存,还可以将其研究思想迁移到对新物相的分析之中,据此确定这些新物相中电子以何种形式存在、是否能够配对等关键信息,因此是从实验上研究超导内禀机制问题的一种重要手段.
3 磁通涡旋运动导致的振荡
超导体中有序与涨落之间的竞争直观表现为磁通涡旋运动导致的量子振荡效应,对这种量子振荡效应的分析有助于深入理解非零温下的超导体系中发生的物理过程.对超导现象的实验观测条件包括温度和外场(如输运测试中的电流场)等,这些外部的能量激发会使超导体系中存在统计涨落,从而引发磁通涡旋运动.目前已经报道了热激发和外电流激发的磁通涡旋运动导致的振荡现象,这些现象对磁通动力学的建立和完善有重要的意义.
3.1 物理机制
如第2 节所述,利特尔-帕克斯效应自提出以来已经在许多复连通结构的超导材料体系中被成功观测到,对该效应的分析还促进了一系列新颖物理机制的发现.但是,也有一些实验观测到的振荡现象并不能用该物理机制进行解释:无论是这些振荡现象的周期、振幅还是振荡的温度依赖关系都与利特尔-帕克斯效应的预测有着明显的矛盾[50,87].为了对这些矛盾进行合理的解释,研究者们以磁通动力学(vortex dynamics)模型为基础,将观测到的振荡现象归因于外磁场下热激发的涡旋-反涡旋对(vortex-antivortex pairs)的运动[48,49,87].进一步的理论分析还表明,与热扰动类似,电流激发的涡旋运动同样会导致这种量子振荡效应的产生[50].
磁通涡旋运动导致的量子振荡效应一方面在物理机制上较为复杂,需要利用时间依赖的金兹堡-朗道方程(Ginzburg-Landau equations)进行解析和数值求解,且求解时还要额外考虑样品的形状和尺寸;另一方面在实验现象上也有不同的表现:一些实验结果观测到了周期性的振荡信号[87],而另外的研究结果却表明这种振荡并未呈现出周期性[50],这与超导体的种类(常规超导体还是高温超导体)、激发源的类型(热激发还是电流激发)、器件的几何结构等多种因素有关.此外,这种量子振荡效应与利特尔-帕克斯效应的振荡条件(复联通结构)、振荡温度区间(超导转变温度区域附近)都有着相似之处,因此实验观测上需要对这两者进行很好地鉴别.一种合理的鉴别手段就是将实际观测到的振荡幅度的温度依赖关系与这两种机制所分别预期的结果进行比较[50,87],将在3.2 节展开介绍.
3.2 研究近况
3.2.1 热激发的磁通涡旋运动导致的磁电阻振荡效应
为了研究有限温度热激发下磁通涡旋的运动行为,巴伊兰大学Sochnikov 课题组[49,87]对刻蚀成特殊图案的高温超导薄膜La1.84Sr0.16CuO4(LSCO)的磁电阻振荡效应进行了分析,并指出了这种量子振荡效应的振幅与利特尔-帕克斯效应之间存在的显著差异.如图7(a)所示,刻蚀后的超导纳米网络可以视为由两组互相嵌套的正方形图案构成,其中大、小正方形的边长分别为500 nm 和150 nm,线宽均为25 nm,该样品的超导转变温度约为29 K.垂直于样品平面施加外磁场后,材料的磁电阻呈现出以类似抛物线形状的电阻-磁场关系为背底的明显的周期性振荡(图7(b)),振荡的周期为∆H ≈950 Oe.结合小正方形边长的尺寸数据算得,该振荡周期对应于Φ0A∆Hh/(2e)(其中A为小正方形的面积).
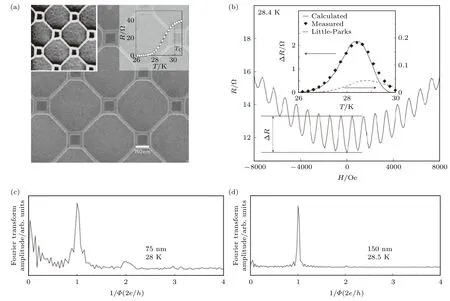
图7 热激发的磁通涡旋运动导致的磁电阻振荡效应[87] (a)高温超导La1.84Sr0.16CuO4 纳米结构的扫描电子显微镜照片,该结构由两个互相嵌套、成角45°的正方形构成,右上角的插图为电阻-温度关系以及据此定义的临界温度 TC;(b) 磁电阻的振荡现象,其中磁电阻的振荡幅度用 ∆R表示.内置插图为振荡幅度 ∆R 与温度的关系(散点图),该振幅远远大于利特尔-帕克斯效应的预测(断续线),却与根据热激发的磁通涡旋的运动模型计算的结果(实线)相吻合;(c),(d) 对振荡曲线作傅里叶变换得到的幅度-磁通倒数关系.其中(c),(d)分别对应于75 nm,150 nm 边长的小正方形.变换后只能在 2e/h 位置处看到一个尖锐的峰,而理论预测的 e/h和 4e/h峰并不显著(图中 4e/h位置的矮峰源于 2e/h 的二倍频信号,并不是本征性质的反映)Fig.7.Oscillation signal observed in magnetoresistance induced by the thermally excited vortex motion effect[87].(a) Scanning electron microscope (SEM) image of a high TC superconductor La1.84Sr0.16CuO4 nanostructure,formed by two sets of square patterns at an angle of 45° with each other.The inset figure at the upper right corner shows the R-T relation and the superconducting critical temperature TC defined in this study.(b) The oscillation phenomena of magnetoresistance,where the amplitude of oscillation is defined as ∆R.The inset figure shows the relation between ∆R and temperature.Note that the amplitude of oscillation is much larger than the expectation based on LP oscillation (dashed line),but is in good accordance with the calculation results based on thermally excited vortex motion effect (solid line).(c),(d) The Fourier transformation results of the oscillation signals,where (c)and (d) are associated with side lengths of 75 nm (c) and 150 nm (d) in the nanostructure patterns,respectively.Only a sharp peak can be observed at the position of 2e/h,but the theory-prospected peaks at the positions of e/hand 4e/h seem insignificant(note that the peak at 4e/hin (c) is just the double-frequency signal of the 2e/h peak,instead of the intrinsic properties of the sample).
为了探究该振荡效应是否属于利特尔-帕克斯振荡,研究者们分别从周期和幅度两方面对振荡进行了分析.虽然上述磁电阻的振荡周期似乎与利特尔-帕克斯效应的预期(h/(2e))完全相符,但问题在于,实验观测到的振荡幅度(定义为 ∆R)却显著大于该理论的预期:实测振荡幅度比利特尔-帕克斯效应所预期的最大振幅[1,44,45,69]仍高出一个数量级以上,且能够观测到振荡的温度范围也与利特尔-帕克斯效应不符,如图7(b)中的插图所示.研究者们将该效应归因于超导纳米环中的“磁通涡旋蠕动”(vortex creep)效应.虽然在二维薄膜中该效应会导致材料的磁电阻随磁场强度增大呈现单调上升关系,但在纳米环结构中,由于运动的磁通与纳米环中电流之间的相互作用,磁电阻会随磁场的变化而展现出振荡现象[48].又因为该振荡磁通的量子化密切相关,故磁通涡旋蠕动效应所导致的振荡周期同样对应于Φ0h/(2e),因此该效应与利特尔-帕克斯效应一样,都是复连通纳米网络呈现出h/(2e) 周期性振荡的原因.
为了从理论上对该振荡结果给出定性的解释,研究者们注意到LSCO 属于高温超导体,这就意味着一方面其相干长度很小,即利特尔-帕克斯效应不会很明显,而另一方面测试温度对应的热扰动能量水平kBTC(其中kB为玻尔兹曼常数)很高,即热涨落对磁通动力学的影响十分显著[48],这两点原因就是研究者们观测到不符合利特尔-帕克斯效应的振荡的原因.除此之外,如2.1 节所述,理论预言高温超导体的磁电阻有可能呈现出以h/e,h/(4e)为周期的振荡[70−73],但根据研究者们对实验结果的傅里叶变换(图7(c)和图7(d))可见,这两种周期的振荡均未被观测到(下图中h/(4e) 位置的矮峰来自于h/(2e) 的二倍频信号,其振幅远远弱于h/(2e) 信号,并非本征性质的反映),这些结果都说明人们对高温超导的理论机制仍在探索之中.概括而言,该工作通过对LSCO 纳米结构中量子振荡效应中振幅、周期的分析,证实了热激发的磁通涡旋运动同样也会展现出h/(2e) 的周期,但可能展现出远高于利特尔-帕克斯效应所预期的振幅.
3.2.2 电流激发的磁通涡旋运动导致的磁电阻振荡效应
另一方面,安特卫普大学的Peeters 课题组、美国阿贡国家实验室Xiao 课题组[50]共同对刻蚀成“梯子”结构的Nb 超导薄膜的含时金兹堡-朗道理论分析与实验验证表明,除了上述热激发机制以外,对超导体施加的电流可以导致磁通涡旋在上述结构中的运动,从而在磁电阻信号中表现出振荡效应.为了建立合适的模型对磁通的运动进行研究,研究者们设计了如图8(a)所示的“梯子”形状的Nb超导结构,其中方形孔洞边长a120 nm,间距d385 nm,“梯子”宽度w385 nm.研究者们细致地测定了超导转变温度附近若干温度点的磁电阻信号,并发现了明显的振荡效应.
为了有力地排除振荡信号源自利特尔-帕克斯效应的推测,研究者们做了两方面的分析:首先,与上文对LSCO 纳米网络的振荡幅度的温度依赖分析[87](图7(b)中的插图)类似,Nb 纳米结构的磁电阻振幅的温度依赖关系无论在振荡可被观测到的温度范围还是振荡幅度上都与利特尔-帕克斯效应的预测[44,45,49,87](由公式∆R0.14(dR/dT)×TC[4ξ(0)/(w+a)]2给出)存在显著差异(见图8(b)中的插图);其次,振荡的周期也与根据样品几何尺寸所预测的利特尔-帕克斯效应的周期并不相符(见图8(c)的上刻度线,无论振荡的峰值还是谷值都没有落在整数个磁通涡旋对应的位置),而与基于电流激发的磁通涡旋运动模型的含时金兹堡-朗道理论分析结果(深蓝色三角形)一致.
除此之外,研究者们还通过理论分析和仿真结果排除了该效应源于热激发的可能:一方面,Nb本身属于BCS 理论范畴内的常规超导体[88],该纳米结构的临界温度也仅有7.6 K 左右(见图8(b)),仅是前文介绍的高温超导体LSCO 的约四分之一.因此,该材料体系中的热涨落水平远远弱于前者,套用基于热激发的磁通涡旋蠕动模型显然并不适合.另一方面,为了合理解释该现象,研究者们又采用电流激发的磁通动力学模型对上述效应的起因进行了分析[48,50].通过对该模型中含时金兹堡-朗道方程的求解,研究者们计算了振荡幅度的温度依赖关系的理论预期值.如图8(b)中插图所示,该理论预测与实验观测到的振幅的温度依赖可以很好地符合,有力地论证了“电流激发涡旋运动”模型的正确性.此外,他们还给出了该材料归一化后的时间平均自由能和电势差的磁通依赖关系,如图8(d)和图8(e)所示.该仿真结果给出了并不依赖整数倍磁通涡旋的振荡效应,与实验结果相符合.此外,研究者们还对不同电流密度条件下的结果进行了仿真,根据仿真结果可以看出,在零磁场、材料处于零电阻态的条件下,增大电流强度可以显著地提高振荡幅度,这与电流激发的磁通运动机制相吻合.
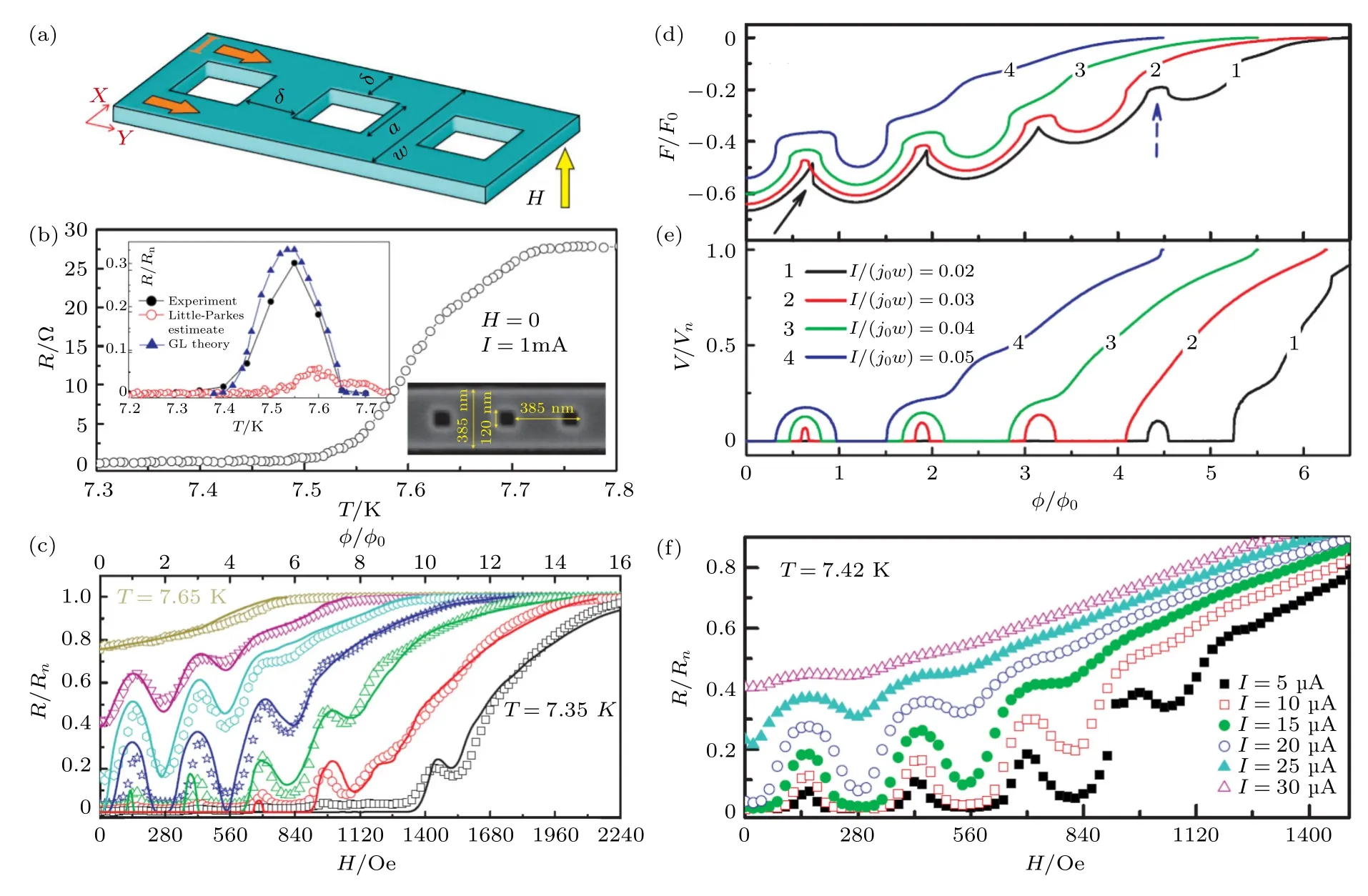
图8 电流激发的磁通涡旋运动导致的磁电阻振荡效应[50] (a) 器件结构示意图.(b) Nb 超导纳米结构的电阻-温度关系,其临界温度在7.6 K 左右.左上角内置插图为磁电阻振幅的温度依赖关系.右下角内置插图为器件的SEM 照片.(c) 7.35—7.65 K 范围内不同温度下的归一化磁电阻测试曲线,温度间隔为0.05 K.磁电阻的振荡周期并不对应整数个磁通涡旋(见上刻度线).(d),(e) 不同电流强度下时间平均自由能(d)和超导纳米结构两端电势差(e)的磁通依赖关系.电势差的变化幅度随着电流强度的增大而增大.(f) 固定温度(7.42 K)、不同电流强度下的归一化磁电阻测试曲线.在零磁场的超导态保持为零电阻的范围内(对应于电流强度在 20µA 以下),磁电阻的振荡幅度随电流强度的增加而增大,与(e)的预期相符Fig.8.Magnetoresistance oscillation phenomena originating from the current-induced vortex motion effect[50]:(a) Schematic diagram of the superconducting Nb device structure.(b) The R-T relation of Nb device.The superconducting critical temperature is approximately 7.6 K.The inset figure in the upper left panel shows the temperature dependence of the oscillation amplitude.The lower right panel shows the SEM image of the device.(c) The normalized experimental magnetoresistance results at temperatures from 7.35 K to 7.65 K.The temperature interval is chosen to be 0.05 K.Note that the periodicity of oscillation does not correspond to integer numbers of magnetic flux quantum.(d),(e) Magnetic flux-dependence of the time-average free energy (d) and electrical potential difference (e) under different intensities of electrical current.The amplitude of oscillation increases with increasing electrical current in (e).(f) Normalized magnetoresistance signal at fixed temperature (7.42 K) with different electrical current.Within the range of I <20µA,the amplitude of oscillation in magnetoresistance increases with increasing electrical current,which is in good accordance with (e).
为了进一步验证该仿真结果的可靠性,研究者们给出了同一温度(7.42 K)、不同电流强度下的磁电阻信号的表征结果,如图8(f)所示.可以看到,零磁场下材料处于零电阻态所对应的电流强度约为I20µA.随着电流强度从 5µA增大到 20µA,磁电阻的振荡幅度确实在不断增加,这与理论仿真的结果很好地符合.该研究指出,磁通涡旋运动导致的振荡并不一定呈现h/(2e) 的周期性[50].并且,由于电学输运测试的过程中外电流的引入不可避免,故这种外电流的引入对实测信号所造成的额外影响应当在超导材料输运性质的研究中引起更高的重视.
综上所述,热激发和电流激发两种机制的磁通涡旋运动都会导致磁电阻信号呈现出振荡效应,这两种振荡效应振幅的温度依赖关系都与利特尔-帕克斯效应振幅的依赖关系显著不同.其中二者的区别在于,热激发的涡旋运动仍然表现出h/(2e) 的振荡周期,而电流激发的涡旋运动导致的振荡却并不是周期性的.
4 韦伯阻塞效应
为了简化凝聚态体系中复杂的多体相互作用,选取合适的表象并抽象出其中的准粒子是一种重要的研究方法.尤其一些准粒子的性质可以相互类比,这使得研究者们能够通过已知准粒子的某些特点预测新的准粒子能够展现出来的性质.量子化的磁通涡旋被视为超导体中存在的一种准粒子,这种准粒子的很多性质与材料中的电子能够进行很好地类比.在2011 年,理论物理学家类比量子点材料中电子的库仑阻塞(Coulomb blockade)效应,认为在足够窄的准一维超导纳米线中能够以磁通涡旋为准粒子观测到类似的效应,并将其命名为“韦伯阻塞”效应[51].该效应在2015 年得到了实验的证实[20],成为利用不同体系中准粒子行为的对偶性来研究物理问题的范本.
4.1 物理机制
前文所述的利特尔-帕克斯效应和磁通涡旋运动导致的振荡效应都是在特殊复连通结构的准二维超导薄膜中观测到的[39,46,49,50,66,75,87].那么,很自然的一个问题就是,普通单连通结构的超导材料中是否也能够观察到类似的超导量子振荡效应? 在2011 年,加州理工学院的Pekker 等[51]通过对超导纳米线中磁通涡旋运动行为的理论分析给出了肯定的答案,并将这样的超导量子振荡现象命名为“韦伯阻塞”效应.
对超导纳米线而言,当其宽度w小于沿该方向的超导相干长度ξ时,由于尺寸的制约,即使沿着垂直纳米线所在平面的方向施加磁场,磁通线也无法进入该超导纳米线之中;但是,如果w略大于ξ,那么磁通线就可能进入纳米线之中,并形成沿长度方向排成一列的磁通涡旋[20](这对纳米线的长度l有严格的要求:如果l超过约5 倍的ξ,则磁通涡旋就会排列成阿布里科索夫晶格(Abrikosov lattice)[51,89,90],也会产生不同的物理效应).这些磁通涡旋本身并不携带电荷,遵循能量最低原理,磁通涡旋之间表现出类似于同性电荷之间的互斥行为,从而导致进入超导纳米线之中的磁通涡旋排成一列.进一步地,当超导纳米线的长度有限时,每当进出一个磁通涡旋都会对纳米线的电输运性质产生显著的影响,从而在磁电阻等信号中展现出振荡,这种振荡就是韦伯阻塞效应[51].
如图9(a)所示,韦伯阻塞效应与横跨超导纳米线的磁通涡旋的运动密切相关.外加磁场时,在超导纳米线两侧的空间中存在若干磁通线,而对这样的超导纳米线施加偏置电流就会驱动这些磁通线发生隧穿,相应地磁通涡旋就会沿着垂直该电流方向发生运动(即横跨超导纳米线),这种驱动力正是量子力学版本的“马格努斯力(Magnus force)”,也就导致超导纳米线两侧的空间视电流方向分别成为磁通涡旋的“源”和“漏”.这些横跨超导纳米线的磁通线影响了沿着超导纳米线方向的电子输运行为:每当一个磁通线跨过纳米线,纳米线两端(绿色区域)就会形成 2π 的相位差,那么根据约瑟夫森结(Josephson junction)效应[91,92],纳米线两端就会产生VΦ0ΓN的电势差(其中ΓN代表磁通线隧穿的净速率)[51].因此韦伯阻塞效应可以表现在磁电阻信号之中,从而很好地解释了此前人们在无定型氧化铟(a:InO)超导纳米线的磁电阻信号中观测到的振荡现象[52];此外,该效应也可以在临界电流-磁场曲线中得到反映(见4.2 节).
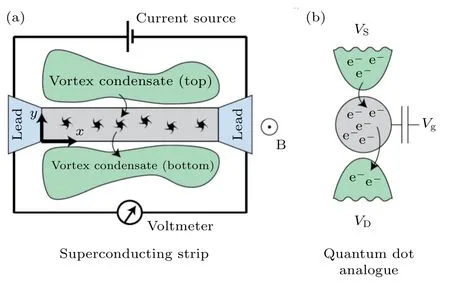
图9 韦伯阻塞效应与库仑阻塞效应[51] (a) 韦伯阻塞效应示意图,其中灰色长方形为超导纳米线,其中的黑色涡旋代表量子磁通涡旋.纳米线两侧(绿色区域)分别构成涡旋的“源”和“漏”,在外加电流的驱动下两端的涡旋发生横跨超导纳米线的运动(如图中黑色箭头所示),磁通涡旋的进出会导致纳米线两端的电压发生变化,即韦伯阻塞效应.(b) 量子点的库仑阻塞效应.量子点(灰色)的两侧分别为电子的“源”和“漏”(绿色),在外加电压的驱动下电子发生源-量子点-漏的运动(黑色箭头所示).对比图(a)与图(b)可知二者之间是电荷-涡旋对偶性的典型体现,韦伯阻塞效应中对超导纳米线施加的电流起到了库仑阻塞效应中源漏间电压 VS–VD 的作用.Fig.9.Comparison between Weber blockade and Coulomb blockade[51]: (a) Schematic diagram of Weber blockade,where the gray rectangle represents superconducting nanowires,and the black vortex represents quantum magnetic flux.The two sides of the nanowire (green regions) are the“source”and“drain”of the vortex.The vortex can move across the superconducting nanowire (shown by the black arrows) driven by the applied voltage.The entrance and exit of magnetic flux will cause a difference in the electrical potential of the nanowire,and this effect is named“Weber blockade”.(b) Coulomb blockade effect of a quantum dot.The two sides (green region) of the quantum dot(gray region) are the“source”and“drain”of electrons,respectively. The electrons move from the source to the quantum dot and finally drain driven by the applied voltage(shown by the black arrows).By comparing (a) and (b),one can see that the two phenomena are appropriate paradigms of charge-vortex duality.
韦伯阻塞与库仑阻塞效应是电荷-涡旋对偶性(charge-vortex duality)[93,94]的一个典例,如图9(a)和图9(b)所示.作为一个准粒子,每个磁通涡旋可以类比为固体中的一个电子,施加的外磁场对应于栅电压,超导纳米线可以类比为量子点(即孤立的库仑岛),流过纳米线的偏置电流就对应于源漏间的电压,而超导纳米线两侧的磁通线进出超导纳米线的过程就可以类比于量子点周围材料中的电子隧穿现象.由于电荷的单位为库仑(Coulomb),对应的上述物理效应称为“库仑阻塞”[95],考虑到磁通的单位为韦伯(Weber),故该效应也就顺理成章地得名“韦伯阻塞”[51].这种电荷-涡旋对偶性使人们可以直接将量子点模型中的种种量子动力学研究成果直接迁移到超导纳米线中磁通动力学的研究之中.从科学的角度上看,这种类比推理的研究方法使研究者们能够根据已有的知识对新材料体系的物性给出比较准确的唯象描述;从应用的角度来看,由于超导量子逻辑电路中的核心材料大多是准一维的超导纳米线,韦伯阻塞效应对超导量子器件基本特性的影响也是制约超导量子计算实用化的一个重要问题.
4.2 研究近况
4.2.1 超导Al 纳米线中的韦伯阻塞效应
为了从实验上证实韦伯阻塞效应的存在,约翰斯·霍普金斯大学 Marković课题组[20]研究了恒定温度(250 mK)下一系列不同长度的超导Al 纳米线的临界电流IC随外磁场强度变化的关系,并在特定强度的磁场范围内成功观测到了韦伯阻塞效应.器件的结构和测试几何如图10(a)所示,其中纳米线宽70 nm(注意到根据金兹堡-朗道理论估算的相干长度约为27 nm,因此二者之间满足上述w略大于ξ的要求)、厚25 nm.电输运性质采用标准四线法进行测试,不同磁场下的临界电流值是通过电流-电压特征曲线(current-voltage characteristics)得到的.其中,在外磁场处于90—130 mT 范围内时,随磁场强度的增加,在电流-电压曲线的转折点对应的电流值表现出了明显的振荡行为,呈现出锯齿型的振荡信号(如图10(b)和图10(c)所示).同时,研究者们通过理论分析表明,当纳米线长度l<100ξ(不超过 2.7µm 时),样品临界电流能够随外磁场变化而呈现出周期性的振荡,且磁场的振荡周期为 ∆HΦ0/(2πlw).实验结果表明,上述振荡信号虽然能够在长达 4.5µm 的纳米线中测出,但当纳米线长度超过 2µm 时,振荡不再有显著的周期性.这些实验结果都与韦伯阻塞的理论预期相符合[51].通过系统研究从零开始施加外磁场过程中样品的临界电流-磁场关系,除了上述韦伯阻塞状态以外,研究者们还观察到了其他状态,如图10(d)所示.根据外加磁场水平的差异,这些状态一共可以分为5 种:1) 当外磁场的磁感应强度小于B0时,材料呈现出完全抗磁性的理想迈斯纳态,表现为IC不随磁场的改变而变化;2) 随着磁场的增大,开始有磁通线进入纳米线,材料变为混合态,IC随磁场的增大而单调下降;3) 当磁场增加到一定程度(对应于图中BS)后,体系中可以观察到明显的韦伯阻塞效应,即IC-B关系呈现出周期性振荡,当磁场大小对应于纳米线中存在整数个磁通涡旋的情况时,纳米线的临界电流取得局域极大值,随着进入的磁通逐渐增加,这些磁通涡旋的间距也不在断减小;4) 当磁场强度增加到BE时,磁通涡旋之间完全接触,沿纳米线中心区域都呈现出正常金属态,而只有两侧的边缘还保持超导电性,此时IC值很小,并随外磁场的增大而缓慢地线性减小;5)体系的临界电流达到零值,整个材料呈现出正常金属态.该工作的意义在于,除了有力地证明在凝聚态理论中基于电荷-涡旋对偶性将量子化的磁通涡旋本身视为一个准粒子[51,93,94]的合理性外,还展现了超导量子器件潜在的应用价值.超导纳米线中的磁通涡旋数目可以通过调整外磁场和电流强度进行调控,类似于基于电荷输运的场效应管(field-effect transistor,FET),基于磁通涡旋的超导器件(flux-based superconducting devices)能够为逻辑电路的构建提供新的可能方案[18,96].
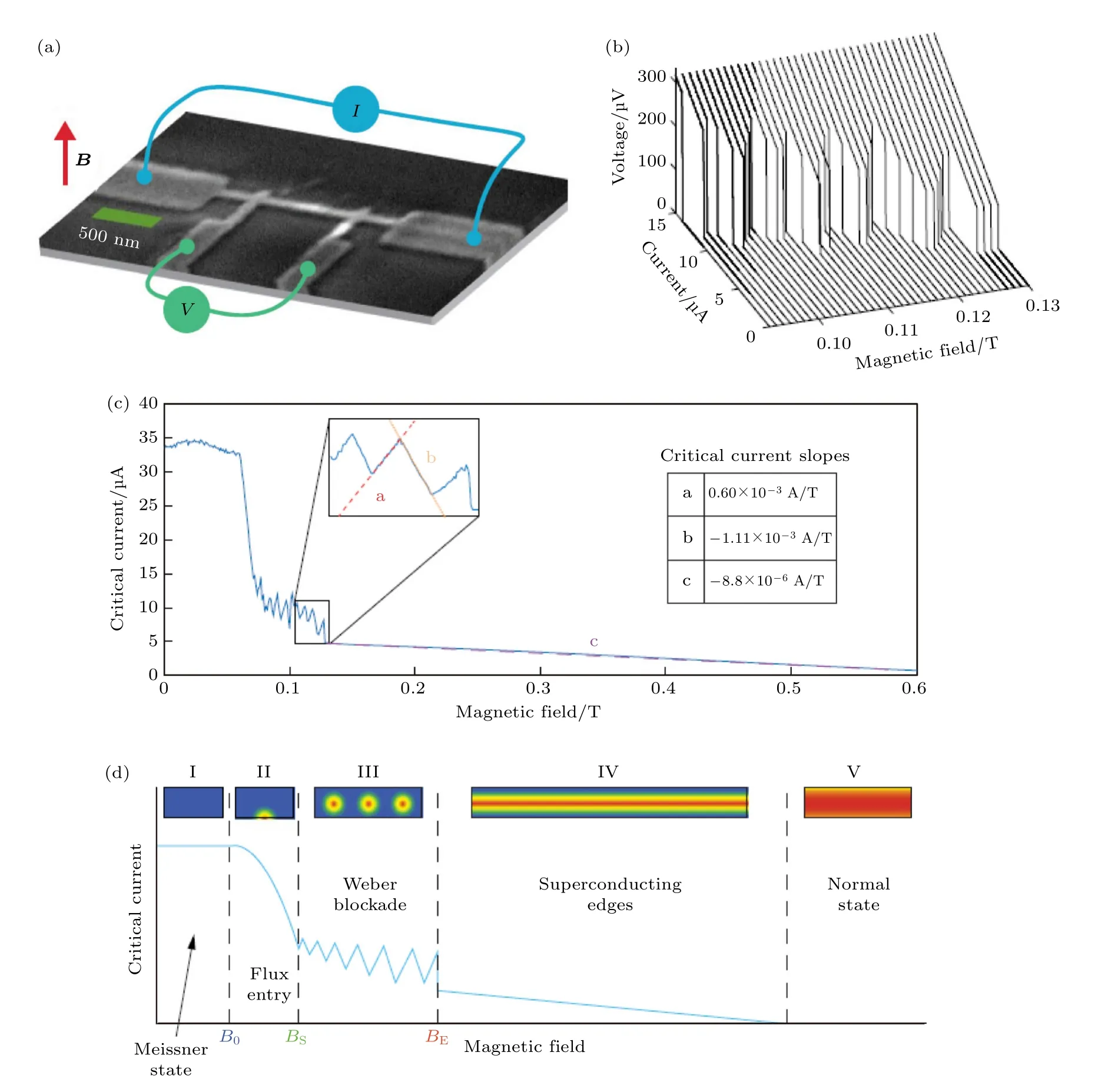
图10 韦伯阻塞效应的实验观测[20] (a) Al 超导纳米线的扫描电子显微镜照片与测试几何示意图;(b) 恒定温度(250 mK)下磁场强度由90 mT 增加到130 mT 时的电流-电压曲线;(c) 根据图(b)的实验结果绘制的临界电流 IC 与磁场的关系.内置插图为曲线在磁感应强度在0.1—0.13 T 范围内的局部放大.标记为a,b,c 的3 个典型区域的临界电流-磁感应强度曲线的斜率标识在右侧表中;(d) 不同磁感应强度下体系所处的状态示意图,随磁感应强度的变化共可以分为5 个区域(以罗马数字标识),每个区域里上面的图代表实空间中纳米线的状态示意图(蓝色区域对应于超导态,红色区域对应于正常金属态,中间颜色为过渡态),下面的图为对应的临界电流-磁场关系Fig.10.Experimental confirmation of Weber blockade[20]:(a) SEM image and characterization geometry of Al superconducting nanowires[20].(b) The I-V characteristics of the nanowire at a fixed temperature (250 mK) with the magnetic field increasing from 90 mT to 130 mT.(c) IC-B relation derived from experimental results in (b).The slopes in the IC-B relation for the regions marked by a,b and c in the enlarged figure are presented in the inset table.(d) The physical states of the system with different intensities of magnetic field.Five typical states (marked by Roman numerals) can be found with the variance of the magnetic field.The upper panel of each region indicates the physical states of nanowires in real space (blue and red colors represent superconducting and normal metal states,and other colors represent transition states).The lower panel shows the corresponding IC-B relation.
4.2.2 金属性超导场效应管中的韦伯阻塞效应
除此之外,在超导场效应晶体管器件的实用化道路上,探明韦伯阻塞效应对输运性质所造成的影响也十分重要[53,64,65].超导场效应晶体管是指以超导体作为沟道的绝缘栅型场效应晶体管.由于超导沟道往往利用宽度很窄的超导纳米线制作,故在外磁场下的超导场效应管也会表现出韦伯阻塞效应.如意大利纳米科学研究院Giazotto 课题组[53]在对金属性超导电流场效应管(metallic supercurrent FET)的研究中就发现了韦伯阻塞效应的踪迹.研究者们设计了同时包含底栅极(back-gate)与侧栅极(side-gate)的金属性超导场效应管,其中导电沟道采用Ti 或Al 超导纳米线制成(图11(a)和图11(b)),纳米线的长、宽、厚度分别为900 nm,200 nm,30 nm.其中,以Ti 纳米线为基础的场效应管的电阻-温度、电阻-磁场关系展现在图11(c)之中.
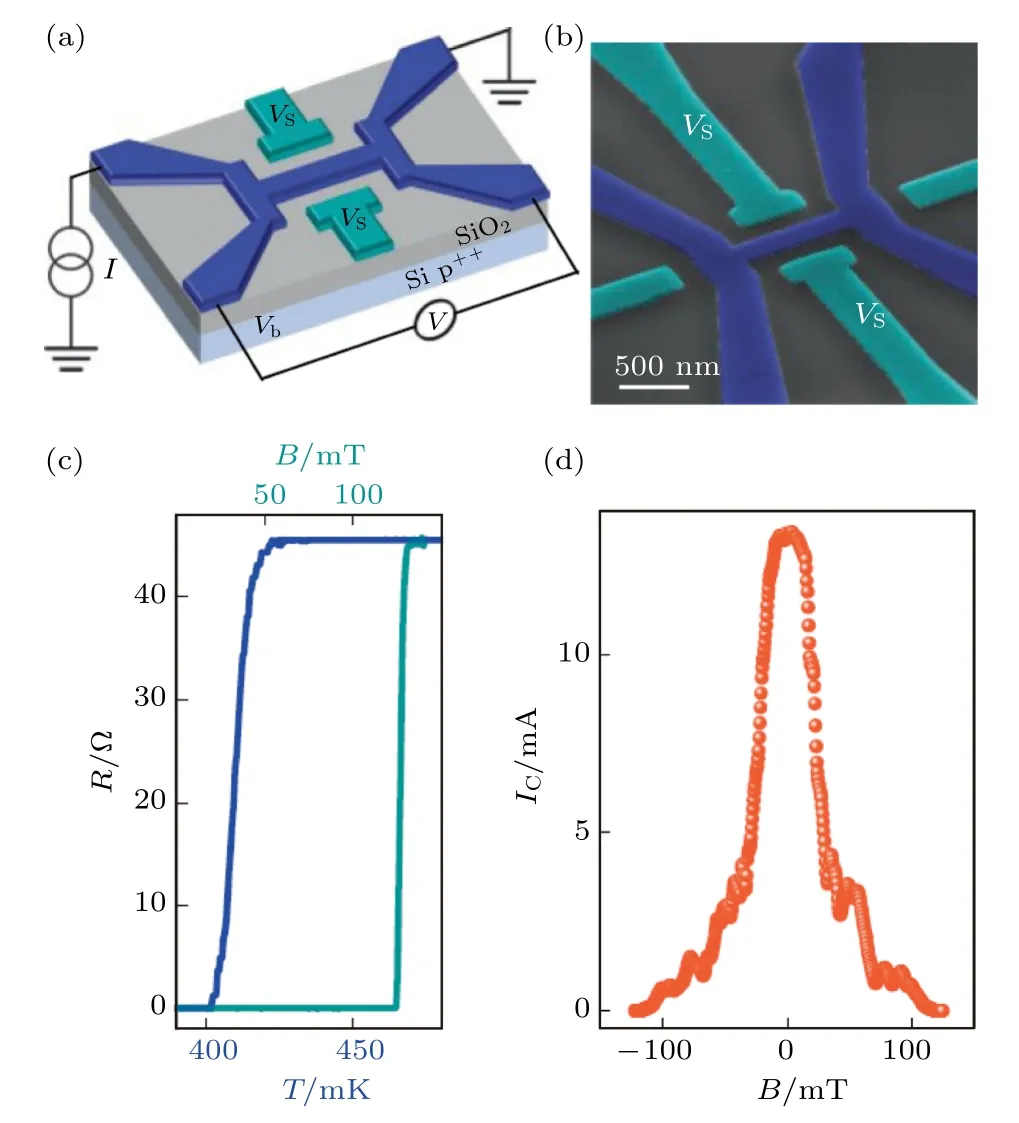
图11 金属性超导场效应管中的韦伯阻塞效应[53] (a)器件结构示意图,其中器件衬底为含有氧化层的重掺杂p 型Si,Vb和 Vs 分别代表底栅级和侧栅级的电势.超 导纳米线(蓝色结构)的电输运行为采用标准四线法测试.(b) 超导场效应管的伪色扫描电子显微镜照片,其中栅极和超导纳米结构分别采用蓝绿色和深蓝色标识.Ti 超导纳米线的长、宽、厚分别为900 nm,200 nm,30 nm.(c) 未施加栅级电压时的电阻-温度关系(深蓝色曲线)与5 mK 下的电阻-磁场关系(蓝绿色曲线).(d) 未施加栅级电压时的临界电流-磁场关系,在磁感应强度为30—100 mT 范围内表现出了明显的振荡行为(测试温度为5 mK),且该行为在施加相反方向的外磁场时也可观测到,与韦伯阻塞效应的预期较为一致Fig.11.Weber blockade effect in the metallic superconducting field-effect transistors[53]:(a) Schematic diagram of the device structure,where the substrate is heavily-doped ptype Si,and Vb(Vs) represents the electrical potential of the bottom (side) gate.(b) Pseudo color SEM image of a superconducting field-effect transistor.“Gate”and superconducting nanostructures are colored cyan and dark blue,respectively.The length,width and thickness of Ti superconducting nanowires are 900 nm,200 nm and 30 nm,respectively.(c) The R-T relation (dark blue line) and R-B relation at 5 mK (cyan line) with zero bias voltage.(d) The IC-B relation with zero bias voltage.Observable oscillation phenomena can be found when the absolute value of the applied magnetic field ranges from 30 mT to 100 mT(the temperature is set to 5 mK).Such phenomena are in accordance with the expectation of Weber blockade.
为了探究韦伯阻塞效应对该超导量子器件的影响,研究者们分别分析了施加静电场和外磁场的情况下场效应管的响应曲线,这里重点关注恒定温度(5 mK)、零栅极电压(Vg0 V)下体系的临界电流IC随着施加不同强度的垂直样品平面的外磁场的变化规律,如图11(d)所示.随着外磁场的强度从零值逐渐增加,超导临界电流值先快速下降,而后在约30—100 mT 的磁场范围内呈现出振荡现象,直至当外磁场达到127 mT 时体系完全变为正常态.上述现象关于外磁场的响应是对称的,即垂直样品平面向上和向下的磁场下的实验结果基本一致.该结果表明,如果想同时利用外磁场和静电场对低维超导场效应管的特性进行调控,那么韦伯阻塞效应带来的潜在影响将不可忽略.
由此可见,通过对韦伯阻塞效应的实验验证及其在超导场效应管器件中的应用,在科学方面,演示了电荷-涡旋对偶性在超导体研究中的重要意义;在技术方面也说明,在超导逻辑电路小型化的过程中,由于纳米结构尺度的缩减,韦伯阻塞效应变得不可忽略,这将导致外磁场下的伏安特性曲线呈现出非单调现象,可能会影响整个器件的工作情况.因此深入对韦伯阻塞效应机制的探索于科学、技术两方面都有重要的意义.
5 总结与展望
综上所述,通过对低维超导材料中超导量子振荡效应的探索,从理论上有望增进人们对超导电子配对机制、磁通涡旋的运动方式等超导材料中的诸多核心物理过程的理解,从而为探究高温超导机制提供了坚实的实验依托;在应用上也为基于磁通量子比特的超导量子计算的研究奠定了基础,是下一代超级计算机器件架构的有力备选方案.因此,对超导量子振荡效应的研究必将成为未来几年,乃至几十年内的重点领域.但另一方面,当前人们对这些量子振荡效应的理解仍然存在不足,典型的科学问题包括以下几点:
1)关于高温超导体的利特尔-帕克斯效应的振荡周期的理论预测与实验结果仍有差异:高温超导体配对机制十分复杂且缺乏合适的理论模型进行描述,而现有模型在预测一些高温超导体的利特尔-帕克斯效应的行为上与实验结果并不一致,如理论预测的d 波配对高温超导体的利特尔-帕克斯振荡周期[70−73]与实验结果[87]并不相符.因此,虽然实验上能够对振荡现象进行准确的测量,但对高温超导体的形成机制的理解仍然是当前研究的短板,也是研究高温超导体的利特尔-帕克斯效应的当务之急.
2)热激发、电流激发的磁通涡旋运动对超导体输运测试信号的影响程度尚不明晰.热扰动kBT所造成的涨落水平、外加电流对涡旋运动的驱动强度都缺乏严格的定量关系[48−50,87].尤其对超导体的电学输运测试往往都是在一定的温度和电流强度下进行的,那么二者之间是否会存在耦合效应、如何分析其对输运测试结果的共同影响仍然存在诸多不明之处,有赖于理论分析和实验检验的进一步探索.
3)韦伯阻塞效应的机制仍有待探索.当前对韦伯阻塞效应的理解主要是利用电荷-涡旋对偶性将量子点库仑阻塞效应的分析结果“迁移”得来的理论[51].虽然能够很好地预期该效应所呈现出的现象并与实验相符[20],但这更多地属于一种唯象的解释,对物理本质触及得不多[51].因此在深入理解其物理机制,比如磁通涡旋运动过程中发生的具体耗散过程等方面仍然存在很多研究空间.
从应用的角度上看,当前基于磁通量子比特的低维超导纳米结构的制作门槛较高、工艺流程复杂、工作温度低,尚不适于大规模工业生产与应用.但也应该看到,如今对传统BCS 超导体的超导量子振荡效应的理解已经比较系统和完善[1,2,97],这也为在高温超导体上将上述量子振荡效应稳定地复现奠定了坚实的基础.相信对高温超导体的种种量子振荡效应研究一旦能够有所突破,必将导致未来超导量子计算的长足进步.
