单层Janus MoSSe双共振拉曼散射的理论研究

孙鸿智，孙薇，赵波，郭怀红

单层Janus MoSSe双共振拉曼散射的理论研究

孙鸿智，孙薇，赵波，郭怀红

（辽宁石油化工大学 理学院，辽宁 抚顺 113001）

单层Janus MoSSe拉曼光谱中出现的双共振峰，是材料特征的重要指纹。但是，这些双共振峰尚存在起源理解不清、机制亟需澄清的问题。基于密度泛函理论、量子高阶微扰理论和群论分析，系统研究了单层Janus MoSSe的双共振拉曼光谱。研究发现，单层Janus MoSSe的电⁃光共振耦合过程的倒格子波矢依赖于激光能量，在第一布里渊区中任意波矢vec都可能出现。基于群论分析，推导出产生双共振拉曼活性的对称性条件，并阐明了在Janus结构体系中出现大量双共振拉曼峰的根本原因。研究结果可为理解二维Janus结构体系中发生的双共振拉曼过程提供理论指导，并为澄清双共振拉曼峰的起源提供合理的理论手段。

双共振拉曼散射； 单层Janus MoSSe； 电⁃光共振耦合

自石墨烯成功剥离以来，大量的二维原子层材料被快速发现和广泛研究。其中，以MoS2、WSe2等为代表的单层过渡金属硫化物尤为突出，不仅为突破硅基微纳器件的摩尔极限提供潜在的材料解决方案，而且因为其中新发现的谷自由度，为信息领域带来了谷电子学这一全新概念[1]。谷自由度主要来自单层材料中时间反演对称性的保持和中心反演对称性的破缺，以及内禀的自旋⁃轨道耦合作用。近年来研究发现，通过多种制备工艺技术，可以将单层过渡金属硫化物转换为Janus结构[2⁃4]，进一步打破了该结构中的镜面对称性，引发了自发的面外极化，极大地改变了过渡金属硫化物的机械性能和光学特性，拓宽了过渡金属硫化物的应用前景[5⁃7]。

拉曼光谱具有快速、准确、无损的优点，在二维材料晶体结构、电子结构和声子结构等表征方面得到了广泛应用。J.Zhang等[3]发现单层Janus MoSSe的一阶A1g拉曼峰完全消失，与结构的面外对称性破缺有关。Y.C.Lin等[4]在Janus WSSe中观察到明显的拉曼峰移动和光谱变宽。G.Chaney等[8]通过计算发现，由于S和Te之间的高电负性差，含有S和Te的Janus过渡金属硫化物具有超高的偶极矩。K.Zhang等[9]利用低频拉曼光谱，发现源于强层间耦合极化的MoSSe/MoS2界面间的电荷转移。

对单层Janus过渡金属硫化物拉曼光谱的研究主要集中在一阶共振过程，对高阶散射共振过程包括双共振过程的研究非常少[10]。单共振牵涉的声子主要集中在布里渊区中心点，与之相比双共振拉曼散射的声子涉及整个布里渊区[11]。然而，Janus过渡金属硫化物结构的高阶共振拉曼，特别是双共振拉曼，由于涉及到光激发下电子的垂直跃迁以及可能覆盖整个布里渊区的电⁃声共振耦合，可以提供诸如电子能带、声子色散谱、电声耦合强度、双声子组合等更丰富的信息[12]。因此，研究Janus过渡金属硫化物结构的双共振拉曼峰是非常有必要的。单层Janus MoSSe在激光能为1.96、2.33 eV激发下的共振拉曼谱[10]如图1所示。

从图1可以看出，单层Janus MoSSe材料中存在大量的谱峰，其中包括4个单共振拉曼峰（红色虚线标注了两个峰和两个1峰）；此外，还有19个用黑色虚线标注的拉曼峰，在不同激光能(1.96、2.33 eV)激发下，这些拉曼峰的峰强和峰位会发生变化，表明拉曼峰来自于双共振散射过程。

针对单层Janus MoSSe中双共振拉曼光谱的峰位起源的问题，基于第一性原理计算、群论对称性分析和量子微扰理论相结合的理论手段，展开系统性研究。通过计算电⁃光共振矩阵元，获得了与激光能密切相关的最可几声子波矢。利用群论不可约表示，分析了双声子组合直积的对称性，结果表明第一布里渊区任意点上的声子组合都有可能贡献拉曼活性的双共振模，这与实验观测到该结构中存在大量非一阶共振拉曼峰的情况相一致。通过对晶格振动的声子谱和高对称、和点的振动模式进行分析，阐明并指派了图1所示的19个未知的非一阶共振拉曼峰的起源。这项结果丰富了Janus过渡金属硫化物的双共振拉曼峰起源研究的内容，并为进一步研究双共振拉曼散射和相关的应用提供了必要的理论参考。

1 计算方法

基于密度泛函理论和Quantum Espresso软件进行结构优化，对电子能带、光吸收谱和声子谱进行计算[13]。计算中电子间的交换关联和离子⁃电子相互作用分别采用局域密度近似(LDA)和带有模守恒的赝势来处理。平面波基矢的能量截断为106Ry，力和能量收敛标准分别为10-5Ry/Bohr和10-6Ry。依据Monkhorst⁃Pack方法[14]，对布里渊区采用15×15×1的点网格设置。为避免层间相互作用，垂直于平面的方向设置了2.7 nm的真空层。

利用费米黄金法则，由式（1）来计算材料的光吸收强度。

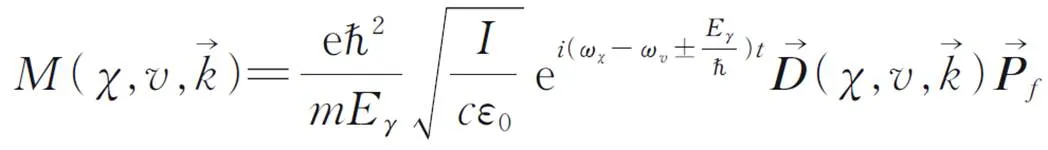
2 单层JanusMoSSe的能带和光吸收

研究双共振拉曼散射过程，首先需要计算电子结构和光吸收谱。单层Janus MoSSe电子能带和态密度及光吸收⁃激光能曲线如图2所示。图中，红色填充区域为实验测量的光吸收曲线，黑线为理论计算结果；红色和绿色虚线分别对应实验采用的1.96、2.33 eV的激光能；导带底和价带顶附近蓝色和黄色标注的能带分别对应自旋向上和向下的带。

（a）电子能带和态密度 （b）光吸收⁃激光能曲线

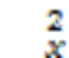
由式（1）和式（2）可知，电⁃光共振过程不仅和能量的匹配函数相关，也和跃迁的选择定则相关。通过式（1）进一步计算了电⁃光耦合强度，即光吸收强度。单层Janus MoSSe电⁃光耦合强度及声子最可几波矢分布如图3所示。为了更好地说明激光能对电⁃光共振耦合的影响，除了使用1.96、2.33 eV两个激光能，还考虑了直接带隙（1.75 eV）和点能隙（2.61 eV）对应的激光能。从图3（a）可以看出，随着激光能增加，电⁃光共振过程逐渐偏离点，形成围绕点的近三角形的电光共振弧，并慢慢靠向点，产生更强的光吸收；在633 nm（1.96 eV）和532 nm（2.33 eV）激光激发下，电⁃光共振过程分别发生在点和点。

一旦受到声子散射，导带电子在不同的共振点或共振弧之间进行谷内或谷间跃迁，产生谷内或谷间的电⁃声共振过程，电⁃光共振和谷间/谷内电⁃声共振相作用，贡献拉曼的双共振散射过程。一旦确定了在第一布里渊区电⁃光共振发生的位置，就可以进一步确定电⁃声共振过程的最可几声子的波矢分布，进而通过声子谱来确定双声子模式的组合贡献。基于图3（a）得到的电⁃光共振的布里渊区点，考虑所有的谷间和谷内的声子辅助的电子跃迁，便可确定最可几的跃迁路径和声子矢量vec。从图3（c）和图3（d）可以看出，随激光能的增加，谷间声子最可几率的vec分布会从点向点转移；在633 nm（1.96 eV）和532 nm（2.33 eV）激光激发下，谷间电声共振耦合分别发生在点和点附近。

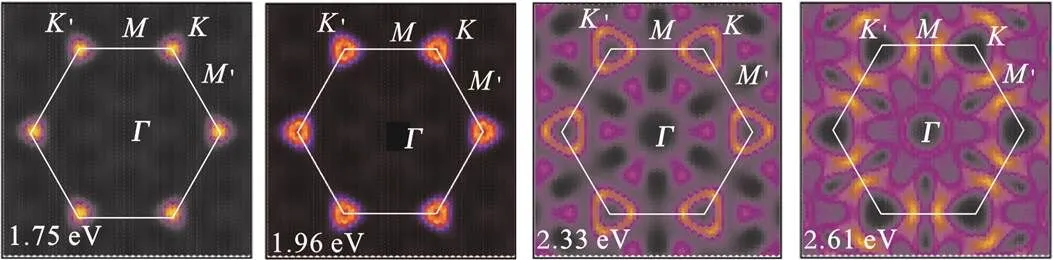
（a）非偏振光的电光耦合强度

（b）左旋圆偏光的电光耦合强度

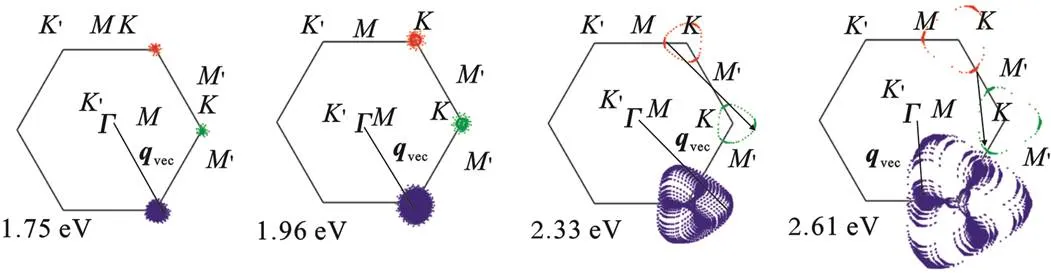
（c）谷间电声耦合的声子最可几波矢分布

（d）谷内电声耦合的声子最可几波矢分布

图3单层Janus MoSSe电⁃光耦合强度及声子最可几波矢分布

从图3（c）和（d）还可以看出，随激光能的增加，谷间声子最可几矢量vec比电⁃光共振的波矢点/弧转移的速度更快，说明在不同的激光能激发下，拉曼光谱中的谷间声子相关的双共振峰的指派需要在特定的动量矢量下进行分析；谷内声子的最可几率的vec几乎分布在布里渊区中心点附近，几乎不随激光能而变化。因此，可以通过改变激光的波长，来观察峰位是否有明显的色散变化，如果没有变化，则可以确认为谷内双声子。

在北京市仁爱教育研究所诉重庆出版社有限责任公司侵犯著作权纠纷案㉖ 重庆市渝中区人民法院（2013）渝中知民初字第108号民事判决书。中，法院就认为，被告利用原告教科书而出版在目录和内容上均与教科书一一对应的教辅书行为，应视为对该教科书在著作权意义上的使用，侵犯了权利人“应当由著作权人享有的其他权利”。因为依据他人编著的教科书出版同步教辅书的行为，虽不同于复制行为，但仍然是作品的使用行为，是教科书著作权人所享有的一项重要的财产权益。虽然立法者未对其进行界定，但应通过兜底条款的适用来保护这一在立法上并未否定的利益。

3 双声子模式的对称性分析

在阐明单层Janus声子谱结果以及双共振拉曼峰的起源之前，先从群论对称性入手，来分析双声子贡献双共振拉曼模式的可能性。分析步骤为：

（1）首先确定声子的波矢以及该波矢所对应的点群。Janus MoSSe结构对应空间点群是3v群，布里渊区从最高对称性的点到、点和最低对称性的一般点，分别对应3v、3、C、1点群。空间点群3v、3、C、1的特征标表见表1-4。表1中，、、表示线性内坐标；、、表示交叉的二次型内坐标；RRR分别表示绕轴的转动轴。表2中，表示是e的指数，、*分别对应120°和-120°（或+240°）转动操作；和*表示两个不可约，但相互不独立，互为共轭。表3中，h表示水平面的镜面对称操作。

（2）利用Birman方法[20⁃21]，借助毕尔巴鄂晶体服务器[22]，确定空间群二阶拉曼散射的选择定则，以及该波矢下两个不可约表示直积的分解系数。

（3）审查分解后的不可约表示中是否含有3v点群的拉曼活性的表示，若有则说明该不可约表示的直积（或双声子的组合）具有拉曼活性，否则就不具有拉曼活性。

表1　空间点群C3v特征标表

表2　空间点群C3特征标表

表3　空间点群Cs特征标表

表4　空间点群C1特征标表

单层Janus MoSSe空间点群的不可约表示的直积及分解和拉曼活性分析见表5-8。表5中，R表示具有拉曼活性。从表5可以看出，所有可能的双声子组合即两个不可约表示直积，除了12和21，分解成的不可约表示都是具有拉曼活性的，这说明在布里渊去中心点（）允许发生倍频模21、22、2以及组合模1+2、1+、2+等双共振模式。由表6可以看出，布里渊区点对应的空间群为3群，从⊗、⊗、⊗*、⊗、⊗、⊗*、*⊗、*⊗、*⊗*可分解成不可约表示1+2、、、、1+2、、、、1+2，都是具有拉曼活性的，这说明在点可能有双共振组合模如2、+、+*、2、2*、+*发生。从表7可以看出，布里渊区M点对应的空间群为C群，从′⊗A′、′⊗″、″⊗′、″⊗″分解成不可约表示都是′+″，并且具有拉曼活性，说明在点允许发生的双共振模式组合模为2′、′+″、2″。从表8可以看出，布里渊区一般对称点的空间点群为1群，直积⊗可分解成不可约表示1+2+2、++*、2′+2″、2都具有拉曼活性，因此在该点允许发生2的双共振模式倍频模。不难得出，单层Janus MoSSe中允许发生的双共振拉曼峰组合的可能性非常多，这就解释了为什么实验观测的共振拉曼谱会出现如此之多的双共振拉曼峰，同时也为这些共振峰的指派带来了困难和挑战。

表5　C3v不可约表示的直积及其分解和拉曼活性分析

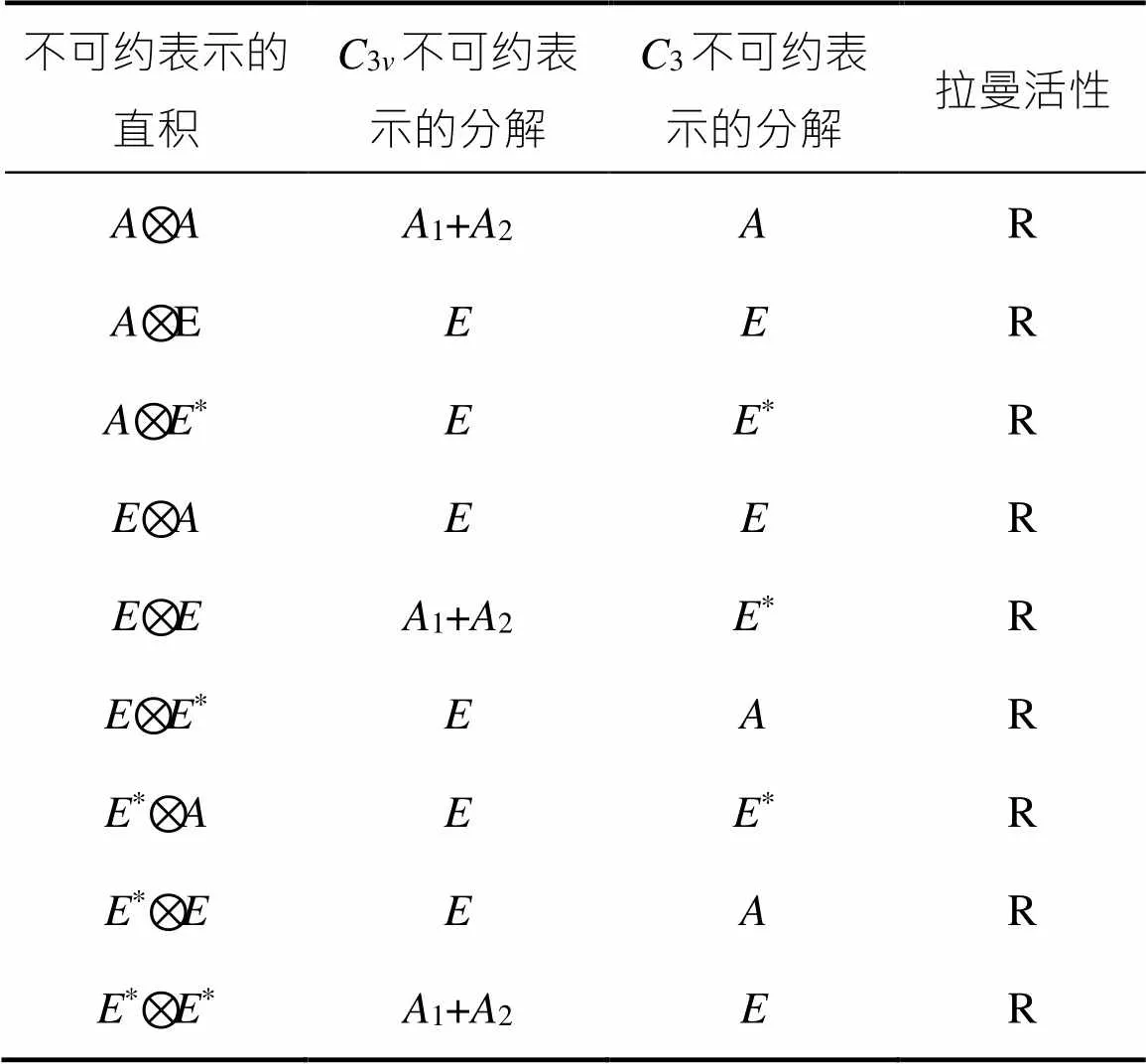
表6　C3不可约表示的直积及其分解和拉曼活性分析

表7　CS不可约表示的直积及其分解和拉曼活性分析

表8　C1不可约表示的直积及其分解和拉曼活性分析

4 双共振拉曼模的指派

单层Janus MoSSe的声子谱和布里渊区高对称点、和点拉曼活性模的可视化图如图4所示。图4（b）中，红色向上箭头代表相加组合模，蓝色向下箭头代表相减组合模，绿色代表倍频模，黑色代表缺陷模。振动模式可视化也能进一步证实上述组合模和倍频模是拉曼活性模。一般来说，拉曼活性模的振动会伴随晶胞面积的明显变化。

图4单层Janus MoSSe的声子谱和布里渊区高对称点、和点拉曼活性模的可视化图

具体理论指派双共振模式的组合方式和频率如表9所示。表9中的峰位指派也暗合了这种规律。

表9　双共振拉曼峰位的双声子指派表 cm-1

从表9可以看出，理论指派的双共振模的频率与文献[10]中测量的共振峰的频率相差不大。与文献[10]中的谱峰指派相对比，认为图1所示的第13个模式应该是点的2TO1倍频模，与文献[10]中的指派发生在点结果不同。通过仔细分析，可以认为文献[10]的指派没有充分的理论依据。除了谷间的电声耦合，还会存在谷内的电声耦合，需要考虑点附近的声子谱数据进行指派，如表9中的第1、14、17峰。此外，其他非一阶拉曼峰的指派结果都在表9中一一列出。

需要指出的是，由于第一性原理计算中使用了赝势方法，不同的赝势会引起频率相应的差值，这是第一性原理计算中原子势近似带来的固有问题。因此，实验和计算频率之间往往也会存在一些差异，计算值往往会比实验值稍小，但可以控制在几个cm-1以内。二阶双共振峰位的指派需要从电光过程、群论分析、声子谱、晶格振动模式可视化等诸多数据出发，很难评估理论计算与实验之间的差异。但是，由于发生在点的一阶单共振拉曼光谱在实验过程中已经确定，理论计算与实验结果之间的差异，即一阶单共振拉曼特征峰峰频的计算值和实验值的差值可以作为参考标准。理论计算获得的4个一阶单共振拉曼特征峰的频率与实验值差2～10 cm-1，这也决定了双共振模式的计算频率值与实验值之间差值0～20 cm-1。依据这个标准指派双共振模式的频率都比实验值稍小，并落在正常的区间。依据以上标准，得到了和文献[10]中给出的4个谱峰13、14、15及17一致的结果。除此之外，还存在其他可能性。例如，模式15除了2LO1（），还存在Z+LO2（）和Z+ZO2（）；模式17除了2ZO1（），还存在LO1+LO2（）。

表9中双声子指派其实还可以通过进一步的拉曼实验设计来验证。从图3（b）中左旋偏振激光的吸收图来看，由于谷的旋光选择性，只有谷存在光吸收，′谷完全没有电⁃光过程发生。在这种情况下，图3（c）中相邻谷和′谷之间就不存在谷间的电声耦合。因此，可以利用单偏振激光进行共振拉曼测量。如果二阶共振峰消失，便可确认谷间双声子的指派是合理的。因此，也期待开展下一步的拉曼测量，来进一步排除或确认理论指派的结果。

由于二维材料中电磁屏蔽效应的极大减弱，会存在明显的电子⁃空穴对的激子效应，不少学者认为计算拉曼谱需要考虑激子效应。本文出于如下原因，没有考虑这个复杂的效应。首先，由于计算处理激子效应需要用到基态电荷密度近似，以及求解复杂Beta⁃Salpeter方程，非常耗时，计算效率低下；其次，在过渡金属硫化物共振拉曼散射的系列研究中发现，激子效应会影响电光矩阵元的强度，即光吸收强度，不会对共振发生的布里渊区的具体位置产生影响。因此，激子效率考虑与否，不会影响最可几声子波矢的位置和相应的双声子的指派结果。

5 结 论

为了阐明近年来成功制备的单层Janus过渡金属硫化物MoSSe结构中双共振拉曼峰位起源问题，将第一性原理计算、群论对称性分析和量子微扰理论相结合，通过电光矩阵元的计算，获得了与激光能密切相关的最可几声子波矢点。利用群论中双声子不可约表示直积的分解，发现布里渊区中心点以外，任意的声子组合都有可能产生拉曼活性的双共振模，与MoSSe材料中观测到的大量谱峰现象相一致，为峰位指派的多样化提供了理论支持。通过声子谱的计算和多个高对称点的振动模式可视化，实验测量的拉曼光谱中的19个模式进行指派，获得了和实验结果一致的激光能色散的结果。当然，未来的工作主要集中在获得电⁃声耦合矩阵元，计算拉曼强度，获得定量化的双共振拉曼计算谱，和实验结果进行直接比对，进而在偏振双共振拉曼方面进行理论指导和实验设计。

［1］ Radisavljevic B， Radenovic A， Brivio J， et al. Single⁃layer MoS2transistors［J］， Nat. Nanotechnol， 2011， 6（3）：147⁃150.

［2］ Lu A Y， Zhu H， Xiao J， et al. Janus monolayers of transition metal dichalcogenides［J］. Nature Nanotechnology， 2017， 12（8）： 744⁃749.

［3］ Zhang J，Jia S，Kholmanov I，et al.Janus monolayer transition⁃metal dichalcogenides［J］.ACS Nano，2017，11（8）：8192⁃8198.

［4］ Lin Y C， Liu C， Yu Y， et al. Low energy implantation into transition⁃metal dichalcogenide monolayers to form Janus structures［J］. ACS Nano， 2020， 14（4）： 3896⁃3906.

［5］ Yang Y， Zhang Y， Ye H， et al. Structural and electronic properties of 2H phase Janus transition metal dichalcogenide bilayers［J］. Superlattices and Microstructures， 2019， 131： 8⁃14.

［6］ Tao W L， Lan J Q， Hu C E， et al. Thermoelectric properties of Janus M（M= Pd， Pt；，= S， Se， Te） transition⁃metal dichalcogenide monolayers from first principles［J］. Journal of Applied Physics， 2020， 127（3）： 035101.

［7］ Wang J， Shu H， Zhao T， et al. Intriguing electronic and optical properties of two⁃dimensional Janus transition metal dichalcogenides［J］. Physical Chemistry Chemical Physics， 2018， 20（27）： 18571⁃18578.

［8］ Chaney G，Ibrahim A，Ersan F， et al.Comprehensive study of lithium adsorption and diffusion on janus Mo/W（，=S，Se， Te） using first⁃principles and machine learning approaches［J］. ACS Applied Materials & Interfaces， 2021， 13（30）： 36388⁃36406.

［9］ Zhang K， Guo Y， Larson D T， et al. Spectroscopic signatures of interlayer coupling in janus MoSSe/MoS2heterostructures［J］.ACS Nano， 2021， 15（9）： 14394⁃14403.

［10］ Petrić M M， Kremser M， Barbone M， et al. Raman spectrum of Janus transition metal dichalcogenide monolayers WSSe and MoSSe［J］. Physical Review B， 2021， 103（3）： 035414.

［11］ 郭怀红，赵波. 拉曼光谱探究二维原子晶体结构和物性的研究进展［J］. 辽宁石油化工大学学报， 2018， 38（6）： 1⁃9.

［12］ Lin M L， Tan P H. Ultralow⁃frequency Raman spectroscopy of two⁃dimensional materials［M］.Singapore：Springer， 2019： 203⁃230.

［13］ Giannozzi P， Baroni S， Bonini N， et al. Quantum espresso： A modular and open⁃source software project for quantum simulations of materials［J］. Journal of Physics： Condensed Matter， 2009， 21（39）： 395502.

［14］ Hartwigsen C， Goedecker S， Hutter J. Relativistic separable dual⁃space gaussian pseudopotentials from H to Rn［J］. Physical Review B， 1998， 58（7）：3641⁃3662.

［15］ Liu H L， Guo H， Yang T， et al. Anomalous lattice vibrations of monolayer MoS2probed by ultraviolet Raman scattering［J］. Physical Chemistry Chemical Physics， 2015， 17（22）： 14561⁃14568.

［16］ Liu H L， Yang T， Tatsumi Y， et al. Deep⁃ultraviolet Raman scattering spectroscopy of monolayer WS2［J］. Scientific reports， 2018， 8（1）： 1⁃10.

［17］ Guo H， Yang T， Yamamoto M， et al. Double resonance Raman modes in monolayer and few⁃layer MoTe2［J］. Physical Review B， 2015， 91（20）： 205415.

［18］ Seixas L， Rodin A S， Carvalho A， et al. Multiferroic two⁃dimensional materials［J］. Physical Review Letters， 2016， 116（20）： 206803.

［19］ Dong B， Wang Z， Hung N T， et al. New two⁃dimensional phase of tin chalcogenides： Candidates for high⁃performance thermoelectric materials［J］. Physical Review Materials， 2019， 3（1）： 013405.

［20］ Saito R， Jorio A， Souza Filho A G， et al. Probing phonon dispersion relations of graphite by double resonance Raman scattering［J］. Physical Review Letters， 2001， 88（2）： 027401.

［21］ Birman J L. Space group selection rules： Diamond and zinc blende［J］. Physical Review， 1962， 127（4）： 1093.

［22］ Aroyo M I， Kirov A， Capillas C， et al. Bilbao crystallographic server. II. Representations of crystallographic point groups and space groups［J］. Acta Crystallographica Section A： Foundations of Crystallography， 2006， 62（2）： 115⁃128.

Theoretical Study on Double Resonant Raman Scattering in Janus MoSSe Monolayer

Sun Hongzhi， Sun Wei， Zhao Bo， Guo Huaihong

（College of Sciences，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

The double resonance Raman (DRR) peaks of Janus MoSSe monolayer are important fingerprints of material characteristics. However, the origin of DRR peaks is still poorly understood and needs urgent clarification. Based on density functional theory, high⁃order quantum perturbation theory and group theory analysis, the DRR spectra of Janus MoSSe monolayer were studied theoretically and systematically. It is found that the inverse lattice wave vector of the electro⁃optical resonance coupling process of Janus MoSSe monolayer depends on the laser energy, and any wave vector may appear in the first Brillouin zone. Based on group theory analysis, the symmetry conditions for the generation of DRR activity were deduced, and the fundamental reason for the occurrence of a large number of DRR peaks in the Janus structural system was elucidated. This study provides theoretical guidance for understanding the DRR processes occurring in two⁃dimensional Janus structural system, and provides a rational theoretical means for clarifying the origin of the DRR peaks.

Double resonant Raman scattering； Janus MoSSe monolayer； Electron⁃optical resonance coupling

O482.31

A

10.3969/j.issn.1672⁃6952.2022.03.006

1672⁃6952（2022）03⁃0030⁃07

http：//journal.lnpu.edu.cn

2022⁃03⁃21

2022⁃05⁃23

辽宁省教育厅面上项目（LJKZ0391）。

孙鸿智（1996⁃），男，本科生，应用物理专业，从事低维材料的双共振拉曼方向研究；E⁃mail：15044517879@163.com。

郭怀红（1980⁃），女，博士，副教授，从事低维材料的物性调控方向研究；E⁃mail：hhguo@alum.imr.ac.cn。

（编辑 陈 雷）