SKPCA⁃LSSVM模型在汽油干点预测中的应用

郭丽莹，李文娜，郎宪明

SKPCA⁃LSSVM模型在汽油干点预测中的应用

郭丽莹，李文娜，郎宪明

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001）

常压塔塔顶汽油干点与产品质量密切相关，因为常减压蒸馏工艺流程和变量相关性均复杂，所以汽油干点预测很难在线进行。软测量方法是解决这类变量估计和控制预测问题的一种技术途径。在核主元分析（KPCA）算法中引入稀疏主元分析（SPCA）思想，采用稀疏核主元分析（SKPCA）算法对模型的输入变量进行选择，实现了数据的非线性降维，简化了主元结构，增加了主元变量的稀疏性。将选择的稀疏主成分作为最小二乘支持向量机（LSSVM）的输入，建立常压塔塔顶干点软测量预测模型。仿真结果表明，SKPCA⁃LSSVM模型相对于传统PCA⁃LSSVM、KPCA⁃LSSVM方法具有较高的预测精度和性能优越性。

软测量； 核主元分析； 稀疏核主元分析； 最小二乘支持向量机； 汽油干点

常压塔塔顶汽油干点直接影响产品的质量、产量，传统技术无法实现对产品质量的实时控制，采用软测量方法对常压塔塔顶干点可以实现在线估计[1]。

近年来，最具代表性的软测量建模方法为支持向量机（Support Vector Machine, SVM）[2]与人工神经网络（Artificial Neural Network, ANN）[3]。李悦卿等[4⁃5]提出了将最小二乘支持向量机（LSSVM）算法与BP神经网络算法作对比，将SVM的不等式约束替换成等式约束，加速了模型求解速度，避免了BP神经网络难以选择合适的参数结构以及局部极小值问题。文献[6]利用核主元分析（KPCA）算法，通过降低样本的维数提取主元，然后使用LSSVM进行建模，降低了模型的复杂性，提高了模型的泛化能力。在LSSVM模型中由于算法本身存在缺陷，计算过程中所有数据样本都被当成支持向量，导致随着样本数量增加，计算难度越来越大。对LSSVM进行支持向量数量的消减，增加模型的稀疏性特征，是LSSVM模型改进的方向[7⁃8]。针对LSSVM模型缺少稀疏性的特征，目前已经提出了很多的改进算法，这些算法以完整数据集作为LSSVM模型的训练样本，导致计算量增加，在模型的预测精度上也需要进一步提高[9⁃11]。

考虑到常减压蒸馏过程中常压塔塔顶汽油干点受很多过程变量的影响，导致所采集的数据维数过高[12]，有必要对辅助变量进行选择和对原始数据进行预处理。KPCA算法借助核函数将变量经过非线性映射转换到高维特征空间来进行特征提取，解决数据间存在的非线性问题[13]。由于KPCA投影到更高维空间再进行降维的过程，计算难度大大增加，工况数据分析时间过长，不利于干点的实时预测。稀疏思想能够自动削弱贡献率小的特征变量，提取重要的特征变量[14⁃16]。

1 基础理论

1.1 KPCA算法原理

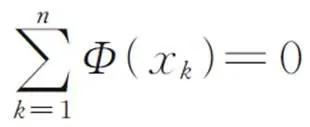
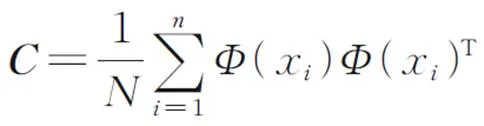
式（4）可以写成:

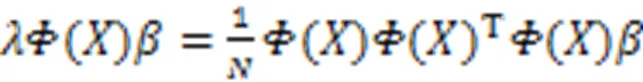
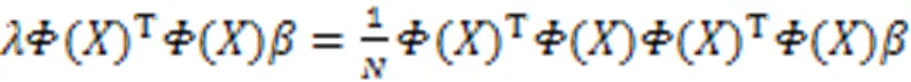
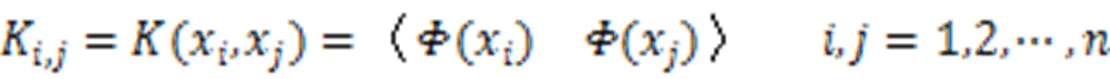
即：

对核矩阵进行中心化处理：

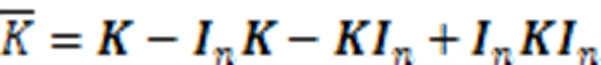
KPCA算法通过在高维空间把非线性数据转化成线性关系来处理，这种方法得到的载荷是空间内所有变量的线性组合，无法突出变量对主元的贡献率，往往是不稀疏的，受噪声干扰明显。

1.2 最小二乘支持向量机(LSSVM)模型

LSSVM是基本SVM的一种扩展[17]。它使用最小二乘损失函数代替SVM中不敏感损失函数，由此将二次规划问题转化为线性方程组求解[18]。LSSVM实际就是一个解线性方程组的过程，降低了计算的复杂性，加快了求解速度。其基本原理为：

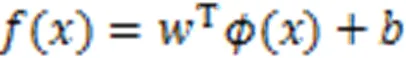
由Karush⁃Kuhn⁃Tucker（KKT）最优条件，得：

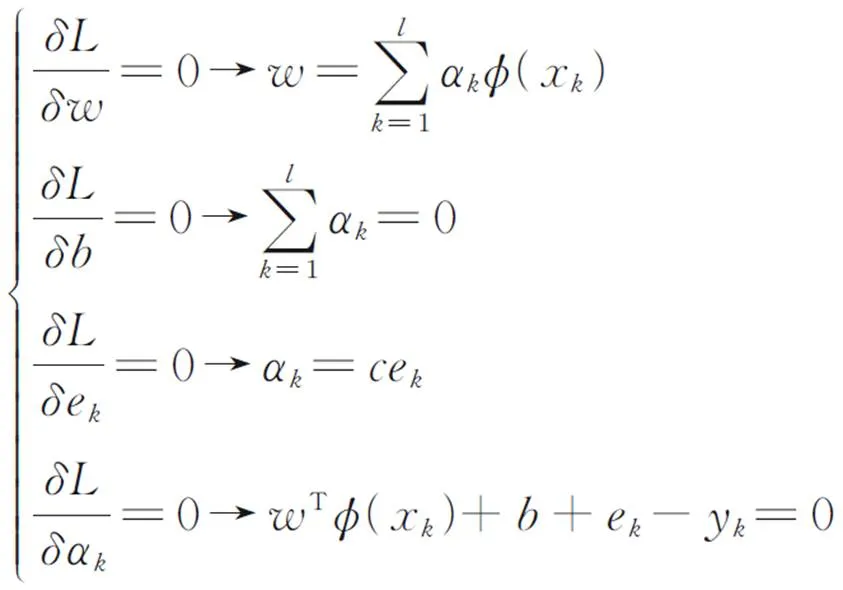
将式(16)写成矩阵：

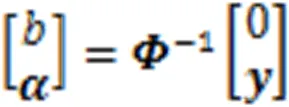
得到最小二乘支持向量机的输出：

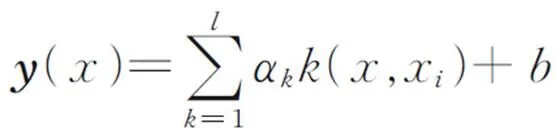
2 改进的稀疏核主元分析

本文提出SKPCA算法，结合KPCA与SPCA，使用核函数投影到高维特征空间，在高维空间内运行SPCA算法，即可以处理非线性数据，也可以使主成分变得稀疏。

文献[19-20]首次说明PCA问题可以改写为带有二次惩罚的回归型优化问题，SPCA模型中包含1罚函数和2罚函数，其策略就是在寻找一个PCA回归优化框架，再通过应用带Lasso惩罚的弹性网直接修正，所以SPCA不仅对原始变量进行降维，而且还使主成分变得稀疏。SPCA模型为：

根据SPCA模型给出SKPCA模型：

KSPCA算法步骤为：

步骤6 重复步骤2-3，直到收敛。

步骤7 标准化之后得到特征值矩阵：

将经过SKPCA处理的数据再作为最小二乘支持向量机模型的输入，可以有效地解决核主元分析算法和最小二乘支持向量机算法缺少稀疏性的问题。

3 仿真实验

为了验证上述SKPCA⁃LSSVM模型的有效性，使用某炼油厂的实际数据进行MATLAB仿真分析。实验使用电脑操作系统为Windows 10，CPU为Intel Core i7，内存为256 GB DDR4。

3.1 辅助变量的选择

根据常压塔塔顶汽油干点这一产品指标，采用软测量建模，选择具有代表性能够覆盖正常运行工况的适当数据作为学习样本训练，输入实时采集的过程参数，模型就会给出相应的质量值，从而实现产品质量指标在线测量的目标。输入变量的选择应基于过程变量的类型、数目和测点位置之间的相互关联，遵循常减压蒸馏过程的机理规律[21]。通过对某炼油厂操作规程的了解，结合现场生产过程数据，初步选择影响常压塔塔顶干点的14个变量（见表1）。

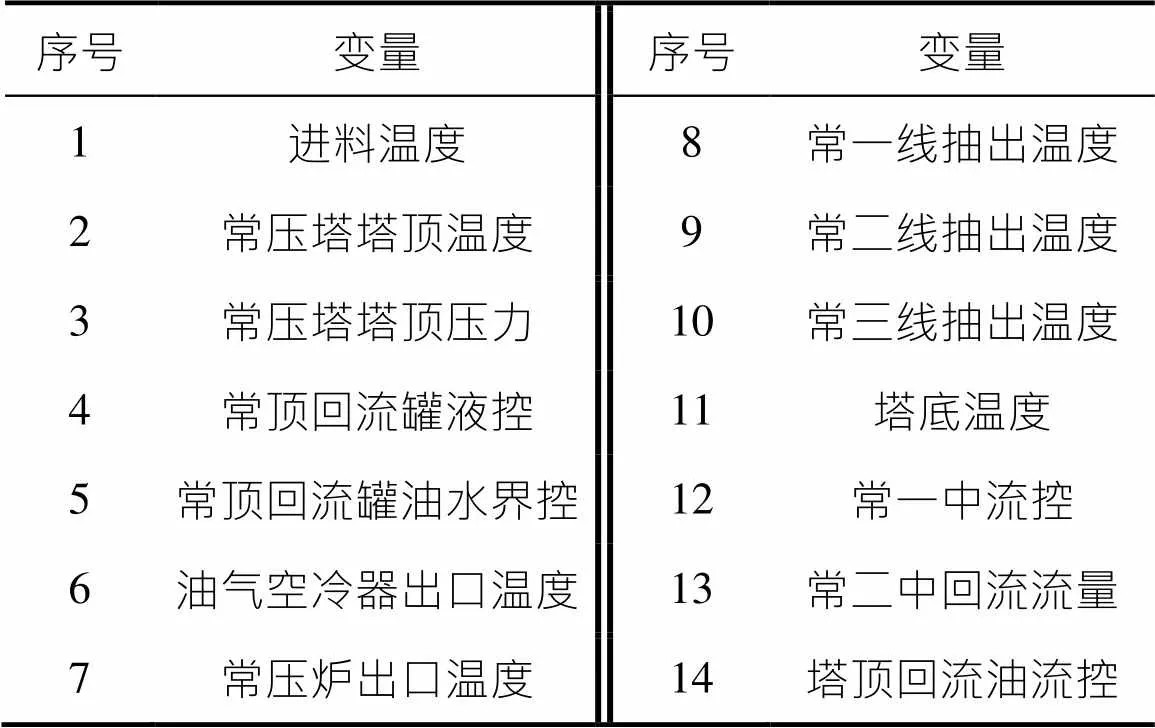
表1　影响常压塔塔顶干点的辅助变量

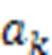
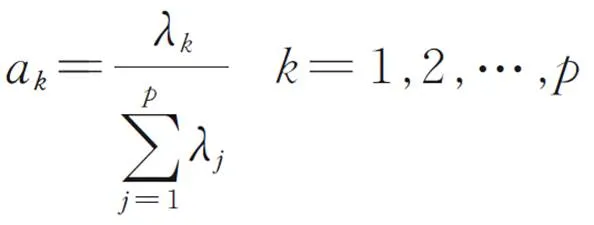
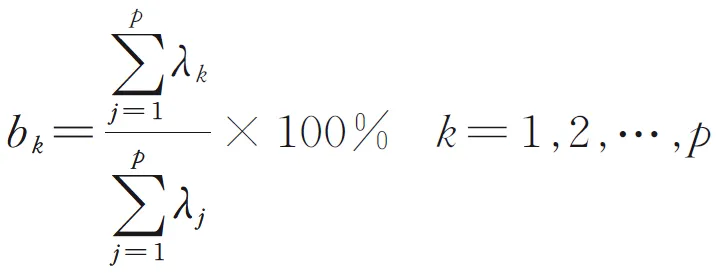
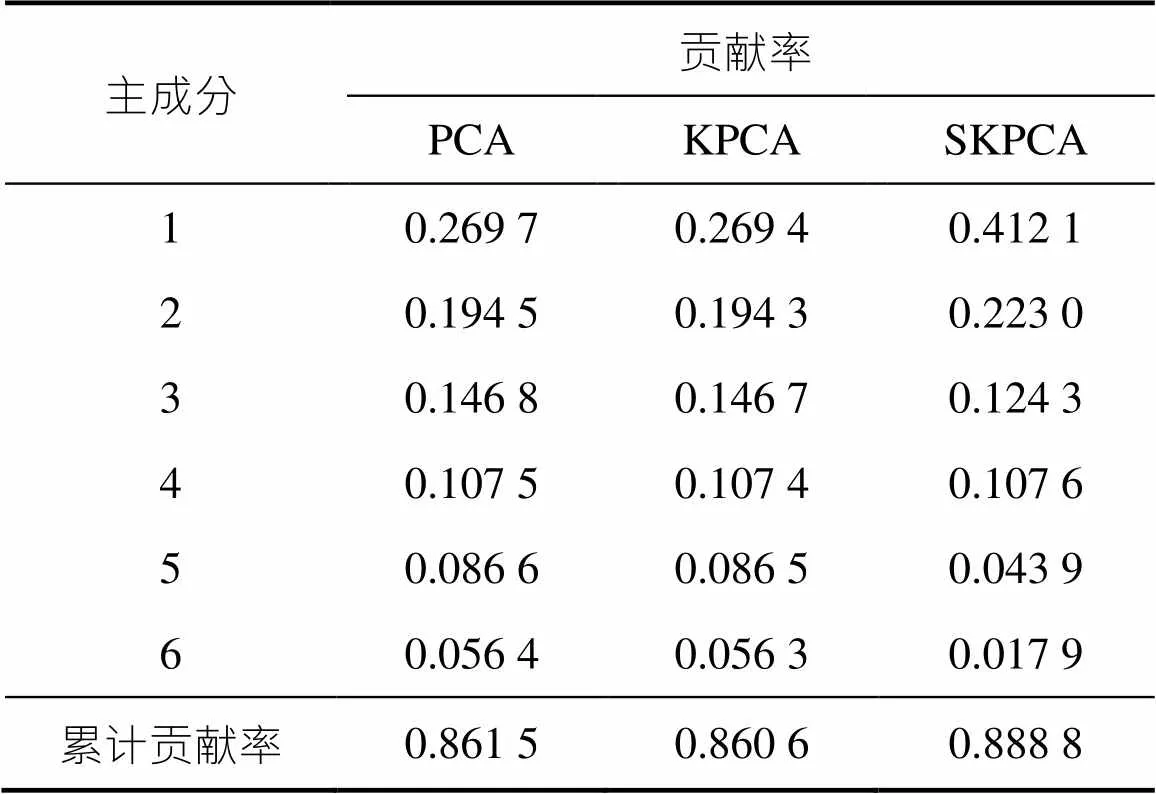
表2　基于PCA、KPCA、SKPCA的贡献率及累积贡献率

3.2 建模过程

分别使用LSSVM、PCA⁃LSSVM、SPCA⁃LSSVM对模型训练和测试，得到原干点数据和预测干点数据的拟合曲线和误差曲线。采用均方根误差(RMSE)和平均绝对误差(MAE)作为模型性能评价准则。

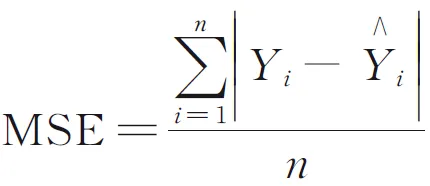
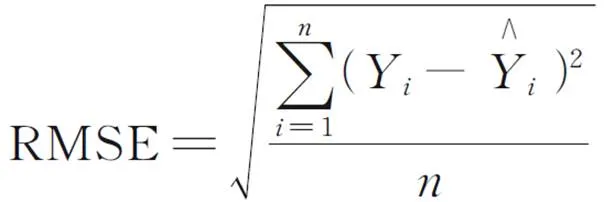
仿真结果如图1所示，模型性能对比如表3所示。

图1　常压塔塔顶汽油干点预测结果及拟合误差

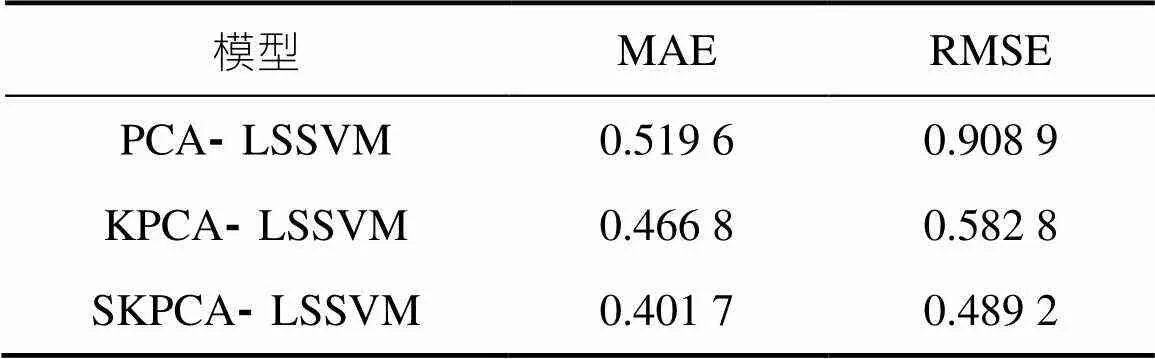
表3　三种模型的性能对比

从图1可以看出，与PCA⁃LSSVM、KPCA⁃LSSVM软测量建模结果相比，在常压塔塔顶汽油干点的预测走势上来看，SKPCA⁃LSSVM软测量建模结果更加逼近真实值，预测精度有了明显改善，基本上能满足工艺的要求；SKPCA⁃LSSVM软测量模型的预测误差比PCA⁃LSSVM、KPCA⁃LSSVM软测量模型的预测误差小，误差波动范围也减小了很多。由表3可知，SKPCA⁃LSSVM模型性能优于PCA⁃LSSVM、KPCA⁃LSSVM软测量模型。因此，SKPCA⁃LSSVM模型具有更好的预测精度和应用前景。

4 结 论

使用软测量方法对常压塔塔顶干点进行预测，分析了KPCA算法和LSSVM算法的缺点，提出了一种基于稀疏核主元分析(KSPCA)数据预处理新方法。首先，将数据映射到更高维的空间，解决了数据在低维空间内存在严重非线性相关问题。然后，在高维空间内对数据样本个主元进行稀疏化处理，减少了无关变量对方差的干扰，提高了主成分的稳定性。将经过SKPCA、KPCA和PCA处理后的数据分别输入到最小二乘支持向量机预测模型中。仿真结果表明，SKPCA⁃LSSVM解决了原始数据之间非线性问题，增加了模型的稀疏性,而且模型性能得到提高。

［1］ 俞金寿.软测量技术在石油化工中的应用［J］.石油化工，2000，29（3）：221⁃226.

［2］ Vapnik V N. The nature of statistical lLearning theory ［M］.New York：Springer⁃Verlag，1995.

［3］ Rumelhart D， Hinton G， Williams R. Learning representations by back propagatingerrors［J］. Nature， 1986， 323（6088）：533⁃536.

［4］ 李悦卿. 基于神经网络和最小二乘支持向量机的软测量技术应用研究［D］.青岛：青岛科技大学，2007.

［5］ 李悦卿，金思毅，陶少辉，等.最小二乘支持向量机用于常压塔汽油干点的软测量［J］.计算机与应用化学，2008（8）：928⁃930.

［6］ 王强，田学民.基于KPCA⁃LSSVM的软测量建模方法［J］.化工学报，2011，62（10）：2813⁃2817.

［7］ Suykens J， Lukas L， Vandewalle J. Sparse least squares support vector machine classifiers［C］// ESANN 2000， 8th European Symposium on Artificial Neural Networks， Bruges：［s.n.］，2000.

［8］ Kruif B， Vries T J A D. Pruning error minimization in least squares support vector machines［J］. IEEE Transactions on Neural Networks， 2003， 14（3）：696⁃702.

［9］ Zeng X， Chen X W.SMO⁃based pruning， methods for sparse least squares support vector machines［J］.IEEE Transactions on Neural Networks，2005，16（6）：1541⁃1546.

［10］ Kuh A，Wilde P D. Comments on "Pruning error minimization in least squares support vector machines"［J］. IEEE Transactions on Neural Networks，2007，18（2）：606⁃609.

［11］ 余正涛，邹俊杰，赵兴，等.基于主动学习的最小二乘支持向量机稀疏化［J］.南京理工大学学报，2012，36（1）：12⁃17.

［12］ 黄德先，江永亨，金以慧.炼油工业过程控制的研究现状、问题与展望［J］.自动化学报，2017，43（6）：902⁃916.

［13］ Wu J N， Wang J， Liu L. Feature extraction via KPCA for classification of gait patterns［J］. Human Movement Science， 2007， 26（3）：393⁃411.

［14］ 彭丽.基于稀疏主成分分析的股票投资组合研究［D］.成都：西南财经大学，2014.

［15］ 喻胜华，张新波.稀疏主成分在综合评价中的应用［J］.财经理论与实践，2009，30（5）：106⁃109.

［16］ 段怡雍. 基于稀疏主元分析的故障检测研究［D］.杭州：浙江理工大学，2019.

［17］ 楼志挺，李春祥.基于空间多点输入的LSSVM非高斯风压预测［J］.上海大学学报（自然科学版），2019，25（6）：1013⁃1022.

［18］ 孙斌，姚海涛.基于PSO优化LSSVM的短期风速预测［J］.电力系统保护与控制，2012，40（5）：85⁃89.

［19］ Zou H.The adaptive lasso and its oracle properties［J］. Publications of the American Statistical Association， 2006， 101（476）：1418⁃1429.

［20］ Zou H， Tibshirani H R. Sparse principal component analysis［J］. Journal of Computational and Graphical Stats， 2006， 15（2）：1⁃30.

［21］ 潘立登，李大宇，马俊英，等.软测量技术原理及应用［M］.北京：中国电力出版社，2009.

Application of SKPCA⁃LSSVM Model in Gasoline Dry Point Prediction

Guo Liying， Li Wenna， Lang Xianming

（School of Information and Control Engineering，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

The dry point of gasoline on the top of atmospheric tower is closely related to product quality, but it is difficult to measure the gasoline dry point online, and the soft sensor is a technical way to solve the estimation and control prediction of such variables. Due to the complexity of atmospheric and vacuum distillation process, the correlation between the variables increases. In this paper, sparse principal component analysis (SPCA) was introduced into kernel principal component analysis（KPCA） algorithm, and the input variables of the model were selected by sparse kernel principal component analysis（SKPCA） algorithm. The nonlinear dimensionality reduction between data was realized, the principal component structure was simplified, and the sparsity of principal component variables was increased. The selected sparse principal components were used as the input of the least squares support vector machine (LSSVM), and the soft sensor prediction model for the top dry point of atmospheric tower was established. The simulation results show that the SKPCA⁃LSSVM model has higher prediction accuracy and superior model performance compared with the traditional PCA⁃LSSVM and KPCA⁃LSSVM methods.

Soft sensor； Kernel principal component analysis； Sparse kernel principal component analysis； Least squares support vector machines； Dry point of gasoline

TE624；TP29

A

10.3969/j.issn.1672⁃6952.2022.03.013

1672⁃6952（2022）03⁃0074⁃05

http：//journal.lnpu.edu.cn

2021⁃03⁃15

2022⁃05⁃19

中国博士后科学基金项目(2020M660125)；辽宁省博士科研启动基金计划项目(2019⁃BS⁃158)；辽宁省教育厅项目(L2020017)；辽宁石油化工大学引进人才科研启动基金项目(2019XHHL⁃008)。

郭丽莹（1996⁃），女，硕士研究生，从事软测量技术原理与应用研究；E⁃mail：guoliying960302@126.com。

李文娜(1976⁃)，女，博士，讲师，从事信号处理、工业过程控制研究；E⁃mail：liwenna0810224@126.com。

（编辑 陈 雷）