基于改进粒子群算法的VSG参数自适应控制策略
2022-07-15郭建祎樊友平
郭建祎, 樊友平
(武汉大学 电气与自动化学院,湖北 武汉 430072)
0 引 言
近年来,随着可再生能源渗透水平的提高,由电力电子器件组成的变流器得到大范围的使用,导致电力系统整体的惯性下降,对系统的稳定运行产生危害,因此,改善变流器的动态响应成为研究的热门之一,在这个背景下,提出了虚拟同步发电机(virtual synchronous generator,VSG)技术。
目前,研究人员对VSG技术进行了大量的研究,从动态特性入手,将VSG技术和同步发电机对比,得到VSG技术的基本特性,并提出可以灵活设计惯性和阻尼参数[1-2]。在参数优化的研究中,大多数文献研究内容集中在设计参数自适应算法对参数进行优化,提出在乒乓算法基础上自适应改变虚拟转动惯量,改善了系统的动态响应[3-4]。文献优化了参数自适应变化的触发条件,以VSG系统的角速度和角加速度的关系为依据,动态分区域判断并调整阻尼系数或是转动惯量,对频率超调抑制能力更强,但参数初始值的计算过程繁琐[5-10];文献结合VSG数学模型提出将阻尼系数和转动惯量灵活配合使用的方法,提升了系统的稳定性,进一步可采用优化算法得到参数初始值[11-12]。
综上所述,现有的研究虽然在一定程度上优化了系统的动态响应,但仍存在不足之处:没有充分利用VSG参数灵活的特点,传统的参数计算过程繁琐,大多数优化系统动态响应的研究并未将系统的电能质量问题考虑在内,参数的优化无法同时考虑多个目标,造成系统的输出电能质量较低,整体控制效果不理想。
针对上述问题,本文以降低系统的输出误差和总谐波失真度为优化目标,利用改进的粒子群算法(particle swarm optimization, PSO)对VSG的参数进行优化计算,然后根据VSG系统的暂态功角特性,通过灵活调节转动惯量和阻尼系数来动态地改变阻尼比,进一步优化系统的动态响应。最后,在MATLAB/Simulink仿真平台上建立VSG系统,以Bang-Bang自适应策略、线性自适应策略和PSO策略、改进粒子群算法(improved particle swarm optimization, IPSO)策略以及常规固定参数策略为对比,验证本文提出自适应IPSO策略的可行性和优势。
1 虚拟同步发电机基本原理
1.1 虚拟同步机模型
传统的VSG系统如图1所示。系统主电路由直流源Vdc、电压型变换器、滤波电路、负载以及交流母线组成,控制回路中,首先采集主电路输出电压、电流、有功功率、无功功率等信号,然后经虚拟调速器、励磁控制器、电压电流双环控制器产生调制信号,最后产生控制变换器的脉冲信号[13-14]。
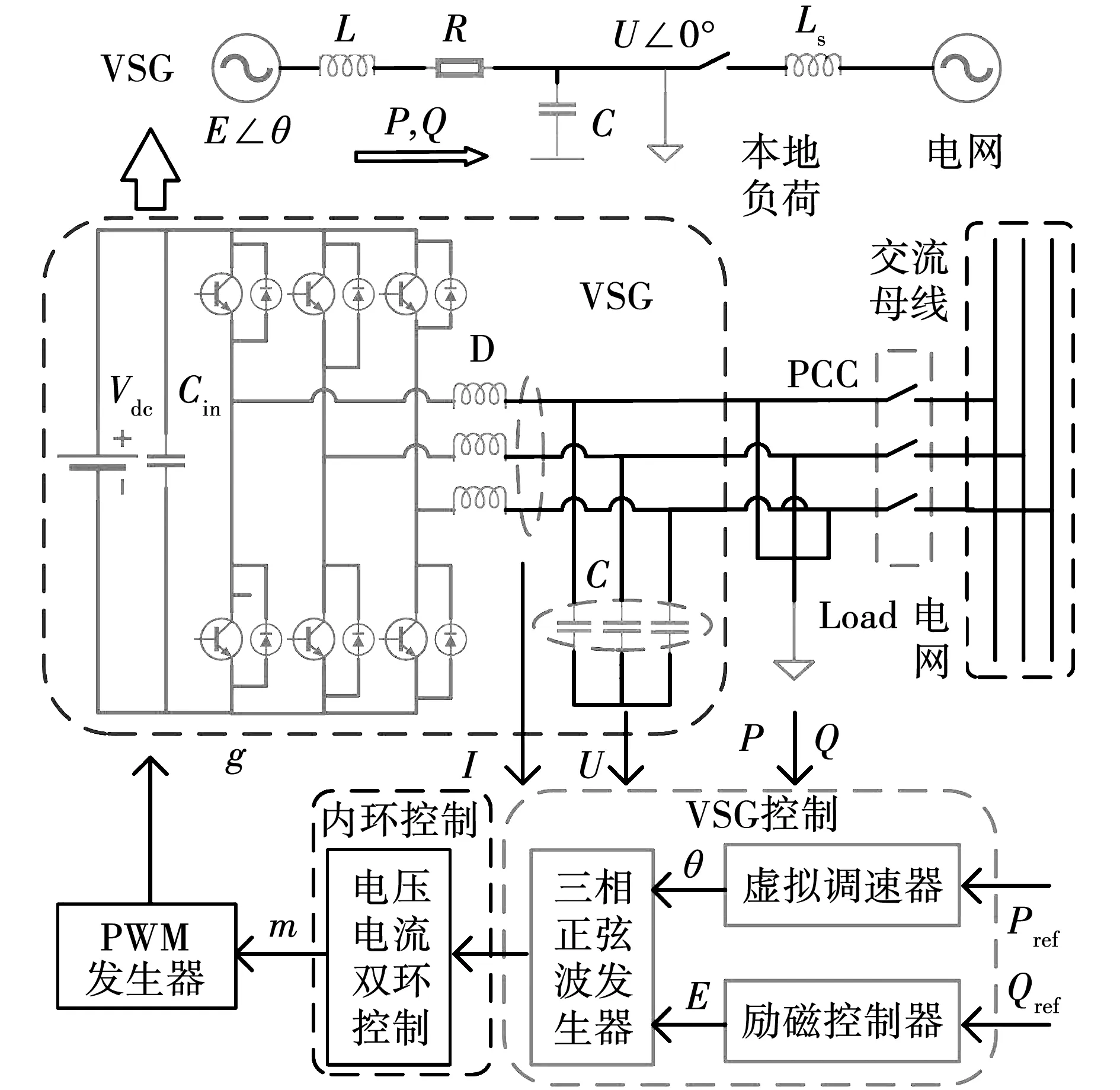
图1 VSG系统图
图1中:L为滤波电感;C为滤波电容;P、Q分别为变流器输出的有功、无功功率;I、U分别为VSG经LC滤波后输出电流和电压。
同步发电机的电气方程和二阶运动方程为:
(1)
式中:R代表定子电阻;X代表电抗;U代表电枢端电压;Tm代表机械转矩;Te代表电磁转矩;D代表阻尼系数;J表示转动惯量;ω表示机械角速度;ω0表示电网侧角速度;Δω表示机械角速度和电网侧角速度之差;θ是输出的功角。
1.2 功频与励磁控制
为了使整个变换器系统能够真正地表现出同步发电机的特性,还需要借鉴同步发电机调速器和励磁调节器的原理,设计出有功调节和无功调节[15]方程为:
(2)
式中:T0为机械转矩指令;kf为调频系数;Pref是给定有功功率;f是虚拟同步发电机机端电压的频率;f0是额定角频率;Pm是虚拟机械功率;kq为无功调节系数;U是输出三相电压额定有效值;Qref是无功功率的额定值;Q为逆变器机端输出的瞬时无功功率值;ku是电压调节系数;Uref是给定电压的幅值;E0为虚拟同步发电机的空载电势;E为虚拟电势指令。
式(1)和式(2)是虚拟同步发电机模型里面主要组成部分,可得到VSG控制原理框图如图2所示。
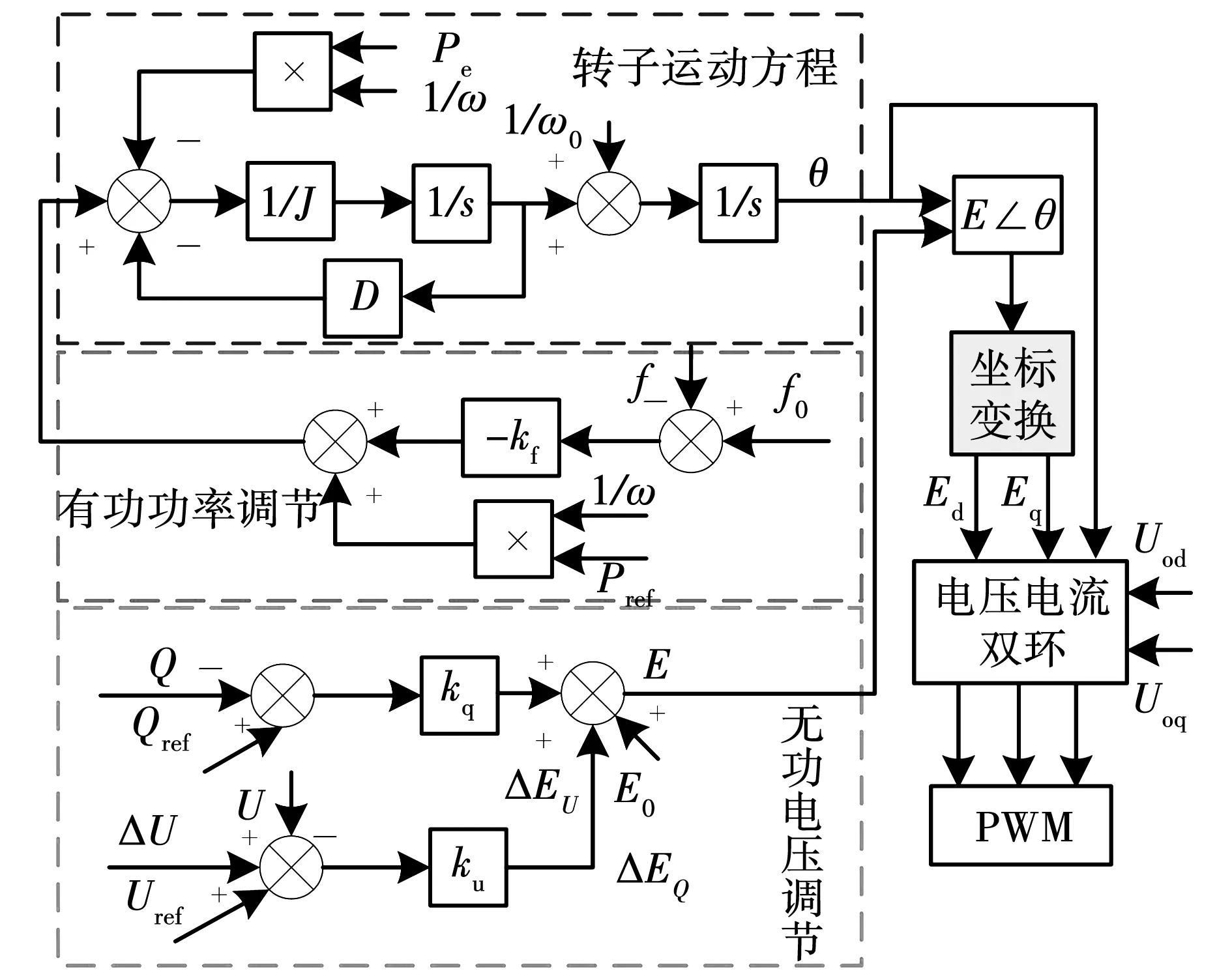
图2 VSG控制原理框图
2 VSG参数计算方法的优化
VSG的运行参数决定了系统的输出特性,目前大多数的研究集中在提升VSG的动态响应方面,忽略了系统的输出电能质量。在考虑系统输出动态响应时,传统的参数计算过程已经十分复杂,若想继续优化系统的输出电能质量就需要使用新的参数计算方法。本文对系统的输出误差以及电能质量进行综合考虑,采取改进粒子群算法对VSG参数进行寻优。粒子群优化算法的原理是模拟鸟群寻找食物的过程,鸟群会根据个体和群体极值动态地调整自身位置,通过迭代求得最优解。粒子群优化算法由于寻优能力强且收敛性好的优点而被广泛运用在各个领域[16-17]。
2.1 适应度函数设计
适应度函数可以用来对粒子位置的优劣程度进行评价,因此适应度函数的选取会对最优解产生影响。误差绝对值与时间乘积的积分(integrated time absolute error,ITAE)是判断误差大小的常用函数;总谐波畸变率(total harmonic distortion,THD)是判断电力系统电能质量的经典依据,将上述两个函数加权后作为本文采用的适应度函数,其中ITAE和THD的表达式[18]为:
(3)
式中:Uzon、Uzo1分别为输出电压谐波幅值和基波幅值;e(t)为输出误差。
适应度函数(fitness function,FF)表达式为
(4)
2.2 粒子群算法的改进
2.2.1 改进惯性权重
在粒子进化初期,过小的惯性权重会减小搜索空间;在后期,过大的惯性权重不利于算法收敛,因此,合理地改变惯性权重有利于得到更优的结果。本文使用的改进惯性权重的算法[19]表达式为
(5)
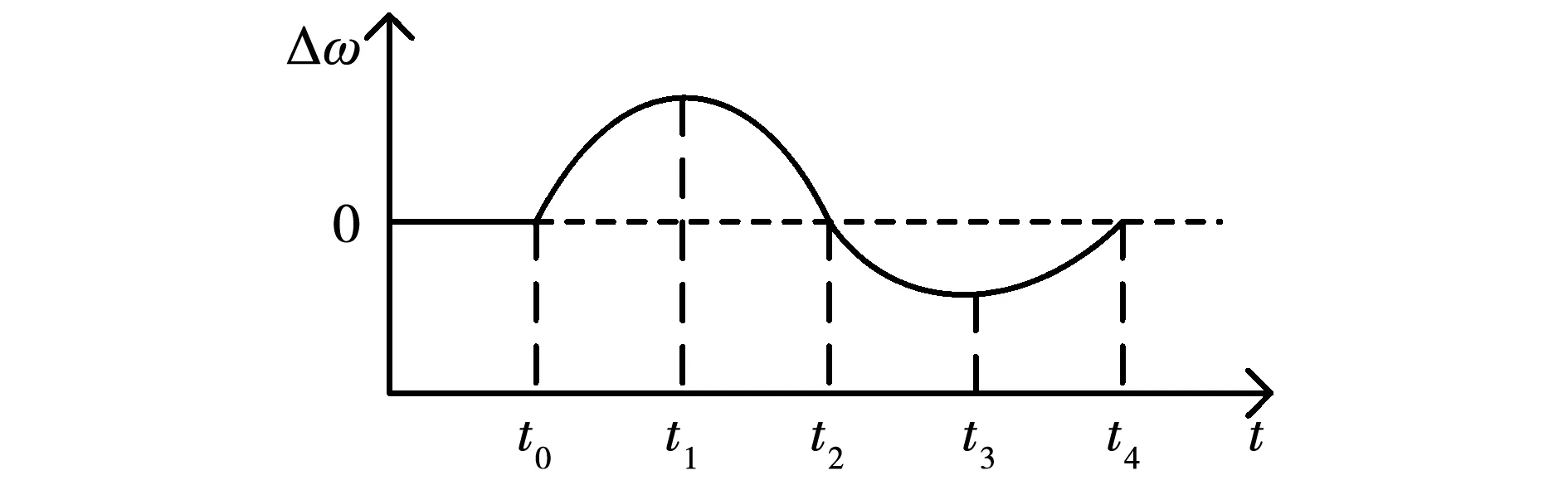
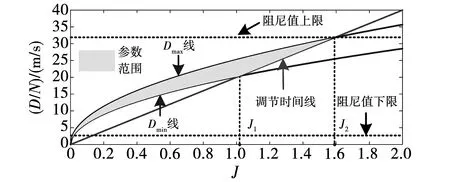
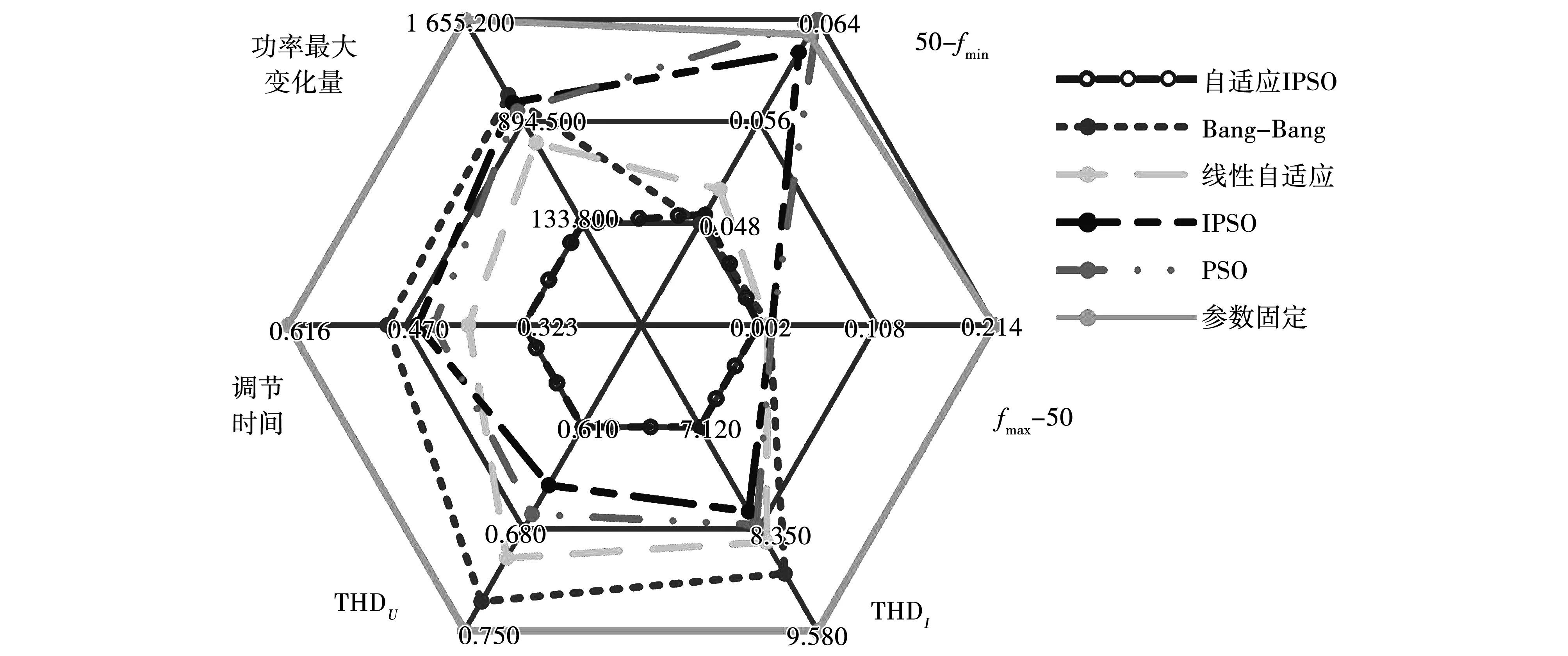
式中:ustart和uend分别为惯性权重的初值和末值,其取值范围是:0.4≤uend 2.2.2 改进学习因子 学习因子会影响算法的全局搜索能力,合理的取值能让算法在初期具备全局的搜索能力,在整个寻优空间进行搜索,在后期尽快收敛到全局最小值,加快收敛的速度。因此,本文通过动态调整c1和c2学习因子来达到此目的,其变化规律[19]为: (6) c2=3+c1。 (7) 式中:cstart为学习因子的初始值;cend为学习因子的最终值。 2.2.3 引入混沌算子 在混沌理论中,混沌系统参数初始值的变化可以影响到系统未来时刻的状态。借助混沌的不重复性,通过引入混沌算子Q来替代粒子的速度更新公式中的随机数r1和r2,从而避免粒子群陷入局部极小。混沌算子Q的计算公式[20]为 Q=xj+1=μxj(1-xj)。 (8) 式中:Q∈(0,1);j=0,1,2,…,M;μ是系统参数,本文取μ=4,此时混沌算子L[21]为 Q=4xj(1-xj)。 (9) 综上所述,改进后的速度更新公式为 (10) 忽略阻尼的影响,转子方程为 (11) 由式(11)可知,转动惯量的大小与系统角速度变化率成反比,因此,可以通过调节转动惯量来控制系统角速度变化率。 对VSG功率回路进行小信号分析,可得有功功率回路的传递函数为: (12) Kp≈3EU/X。 (13) 式中:X为等效阻抗;典型二阶系统的固有角频率ωn和阻尼比ξ表达式为: (14) 进一步由式(14)可得系统阻尼比随转动惯量与阻尼系数的变化趋势,如图3所示。 图3 阻尼比和调节时间 由图3(a)可知,在VSG系统中,阻尼比ξ的大小与阻尼系数D成正比,与转动惯量成反比;由图3(b)可知,阻尼系数与系统调节时间成反比,转动惯量与系统调节时间成正比。因此,可以通过调整转动惯量和阻尼系数的大小来改善系统的阻尼比,进而改善其动态响应。 传统VSG系统的转动惯量和阻尼系数均为恒定值,无法达到最优的控制效果。本文从VSG系统对参数的需求方面进行分析,对参数控制理论进行改进。在扰动情况下,系统的角速度变化量随时间的变化情况如图4所示。选取其中5个时间点:分别对应t0、t1、t2、t3和t4,根据频率偏差和频率变化率的变化情况来调整系统的转动惯量和阻尼系数[22]。 图4 Δω随时间的变化图 区间1(t0~t1):系统给定功率在t0之前维持不变,在t0时刻突然增加给定功率,根据转子运动方程可知,角频率会增加,电能转化为动能,dω/dt从0突增,此区间内dω/dt>0且Δω>0,在t1时刻系统输出角频率最大,此区间应该增大转动惯量,降低系统的角速度变化率,与此同时,减小阻尼系数。此时转动惯量与阻尼系数的调节规律[23]为: (15) 式中:J0、D0分别是稳定运行时的转动惯量和阻尼系数;k1、k2和m1分别为比例系数和指数系数。 区间2(t1~t2):此时系统的dω/dt<0,虚拟转子角频率在t1~t2由最大值开始减小并恢复到初始值,这个过程中系统的Δω>0,应取较小的转动惯量来快速到稳定状态,同时应增大阻尼系数来避免系统阻尼比过小而导致的系统频率震荡现象。因此,转动惯量和阻尼系数的调节规律为: (16) 区间3(t2~t3)与区间4(t3~t4)分析过程与前面的相似。但由于过大或者过小的参数均会降低系统的稳定性,因此应注意以下3点: 1)针对区间1的调节规律,若转动惯量和阻尼系数的计算值不在合理范围内,则应选取相应的上限值或者下限值。 2)为了避免参数过于频繁地改变,需要设置一个触发自适应函数的阈值。 3)转动惯量稳态值J0与阻尼系数稳态值D0是通过第2节的优化算法得到的。 综上所述,改进的参数控制理论可归纳为: J= (17) D= (18) 式中:Jmax、Jmin、Dmax、Dmin分别是转动惯量和阻尼系数的最大值、最小值;NJ、ND是频率变化率的阈值。式中参数的取值详细推导过程参考文献[23],转动惯量和阻尼系数稳态值通过前面改进的粒子群算法得到。 在设计系统时,需要综合考虑系统的调节时间、响应速度等性能,一般设计系统的阻尼比在(0.8,1)之间。其次,需要考虑有功功率环的稳定性,有功功率环可以看作一个二阶系统,其幅值裕量h和相位裕量γ的表达式[24-25]为: (19) 通常,幅值裕量h大于0,相位裕量γ在30°至80°之间。为方便计算,本文取γ>60°,可以得到如下范围: Re(si)=-D/2J≤-10。 (20) 综上所述,结合式(19)中阻尼比的取值范围得到转动惯量和阻尼的取值范围如图5所示(本文设置的额定容量为50 kVA),图中阴影区域是合理的取值区间。 图5 转动惯量与阻尼系数取值范围 Dmax和Dmin包络线的取值通过式(14)、式(20)得到: (21) (22) 有功功率环的开环传递函数在截止频率时需要满足[25]: (23) 为了保证系统动态响应的调节时间在合适的范围内,需要保证 (24) 即 D≤31.83。 (25) 可得转动惯量和阻尼的取值范围为: (26) 因此,当系统的转动惯量和阻尼系数在式(26)范围内自适应变化时,能够保证系统的阻尼比在(0.8,1)之间,进而能够维持系统的稳定性。 综上所述,本文的核心算法流程图如图6所示。 图6 IPSO自适应参数控制策略 为了对本文提出的控制策略进行验证,本文在MATLAB/Simulink平台上搭建VSG系统仿真模型,采用的相关控制参数如表1所示。 表1 仿真参数表 算法运行参数如表2所示。 表2 算法运行参数 算法运行过程中的适应度函数曲线如图7所示。可以看出,两种算法均可靠收敛,IPSO算法拥有更快的寻优速度,精度也优于PSO算法,并且IPSO算法的最终适应度函数值更小,证明IPSO算法收敛结果相对PSO算法更接近全局最优值,优化得到的参数如表3和表4所示。 图7 适应度函数曲线 表3 PSO优化结果 表4 IPSO优化结果 4.3.1 对比方案设计 为了验证本文所提方法在抑制系统输出波动和改善输出电能质量方面的优势,选择Bang-Bang自适应策略、线性自适应策略、IPSO优化策略、PSO优化策略以及传统固定参数策略作为对比,对比方案的参数设计如下: Bang-Bang自适应策略核心公式[26]为: (27) (28) 根据前文对转动惯量和阻尼系数变化范围的限制,这里设置Jmax为1.5、Jmin为0.5、Dmax为25、Dmin为15,当两者均为最大值时,阻尼比为0.81,当两者均为最小值时,阻尼比为0.841,均在合理范围内。 线性自适应策略的核心公式[27]为: (29) (30) 依然在前文计算得到的参数范围内设计线性自适应策略的参数,J0取值为0.9,D0取值为19.1,阻尼比为0.80,kj取值0.23,kd取值1.02。 IPSO策略与PSO策略的参数取值按照前面仿真结果设置。传统固定参数策略的J取值为1.1,D为1.5,阻尼比为0.57,其余参数和表2保持一致。 4.3.2 仿真结果 有功功率给定值的改变会对电网稳定造成影响,因此本文在0.5 s时模拟系统减小5 kW的有功功率指令,仿真结果对比如图8~图12所示。 图8和图9是本文方法和对比方法的调节过程中频率与功率变化曲线。由图8可知,在0.5 s时系统的功率给定值发生变化,导致系统频率发生波动,本文控制方法可使系统频率在0.823 s重新进入稳态,是所有方法中最快的。由图9可知,系统输出功率随着给定值变化而变化,在调节过程中,传统参数固定方法的功率超调量为1.66 kW,相比之下,本文控制方法的超调量只有0.13 kW,有效抑制了输出功率的超调现象。 图8 输出频率曲线 图9 输出有功功率曲线 图10和图11是调节过程中转动惯量和阻尼系数变化曲线。在0.5 s时,系统给定有功功率由20 kW降低到15 kW,此时系统给定功率小于负载功率,系统频率降低,dω/dt<0,根据前面的分区可知,此时系统处于区间3。由图10(a)可知,本文方法可以控制系统的转动惯量在0.5~0.56 s之间按照式(15)自适应变化,其中0.5~0.521 s之间自适应数值大于上限值,按照算法的原理取上限值,0.521~0.56 s则按照自适应计算值变化;由图11(a)可知,阻尼系数在0.5~0.56 s之间自适应变化,且数值无越限。 图10 转动惯量曲线 图11 阻尼系数曲线 图12是调节过程中阻尼比的变化情况。本文控制策略在0.5~0.56 s提供给系统较小的阻尼比,加快系统输出频率达到峰值的速度,缩短调节时间。在0.56~0.57 s之间,系统的输出频率从峰值向稳态值恢复,控制策略使得阻尼比迅速增大,避免系统发生频率振荡现象。PSO、IPSO参数优化策略与固定参数策略的阻尼比均不变,线性自适应策略和Bang-Bang自适应策略的阻尼比在受到波动后均自适应改变,与前面的理论设计相符合。 图12 阻尼比曲线 选取输出结果的频率最大值、最小值与50 Hz的偏差量、ΔPmax、调节时间、三相输出电压和电流的波形畸变率作为评估指标,其中波形畸变率是通过对系统输出电压和电流在0.5 s后的10个周波进行分析得到的,结果如图13所示。 根据图13可知,参数固定策略的整体控制效果最差。IPSO策略在电压波形THD、电流波形THD、频率差值方面均优于PSO策略,证明了IPSO算法的参数寻优结果更好。IPSO策略和PSO策略的波形THD指标均优于常规自适应算法,但常规自适应算法在抑制输出波动方面效果更好。本文使用的自适应IPSO策略能够在对系统输出电能质量进行优化的同时改善系统的动态响应,综合控制效果优于其他方法。 图13 系统输出指标雷达图 传统的虚拟同步发电机技术虽然能够通过模拟同步发电机的运行特性来提高系统的稳定性,但仍存在参数设计过程复杂、无法同时兼顾多个性能指标进行参数设计、调节时间长、暂态超调大的问题。针对这些问题,本文利用一种基于改进粒子群算法的VSG参数自适应控制策略来解决上述问题,并通过仿真验证了该方法的有效性,主要工作与贡献如下: 1)通过改进惯性权重和学习因子并引入混沌算子对粒子群优化算法进行优化,进一步提出以降低系统的输出误差和总谐波失真度为参数的优化目标,利用改进后粒子群算法对VSG系统参数进行优化。 2)分析了虚拟同步发电机系统的转动惯量和阻尼系数对系统频率稳定性的影响,然后根据系统的暂态功角特性,对传统VSG系统参数控制理论进行了改进,并设计了相应的自适应控制函数。 3)通过仿真将现有的VSG控制策略和本文的控制方法进行了对比。结果表明,本文的控制方法能够避免系统参数复杂的计算过程,提高系统输出电能质量,改善系统的动态响应,控制效果更好。3 VSG参数控制策略的改进
3.1 VSG参数对系统的影响

3.2 参数控制理论的改进
3.3 考虑系统稳定性的参数范围计算

4 仿真分析
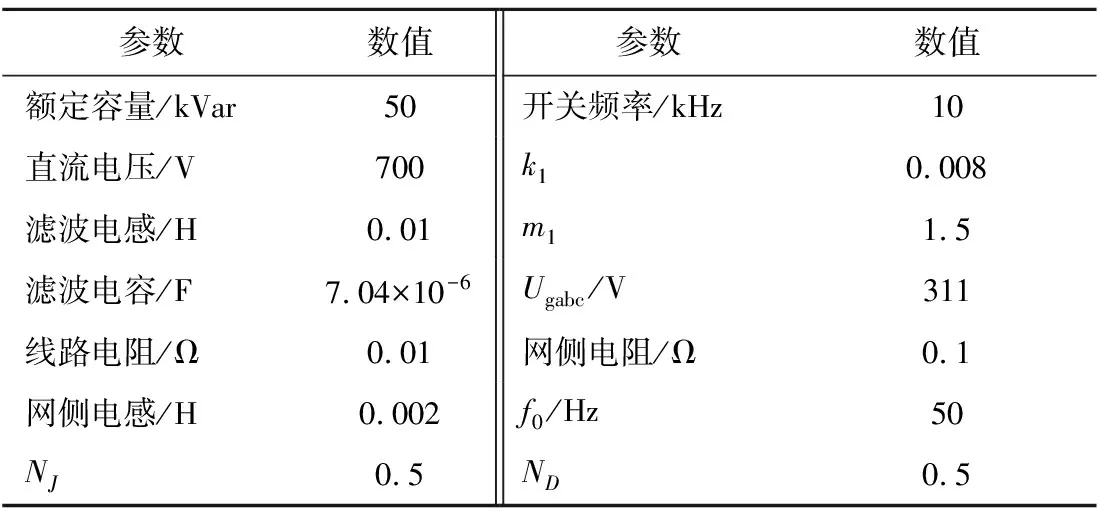
4.1 参数设置
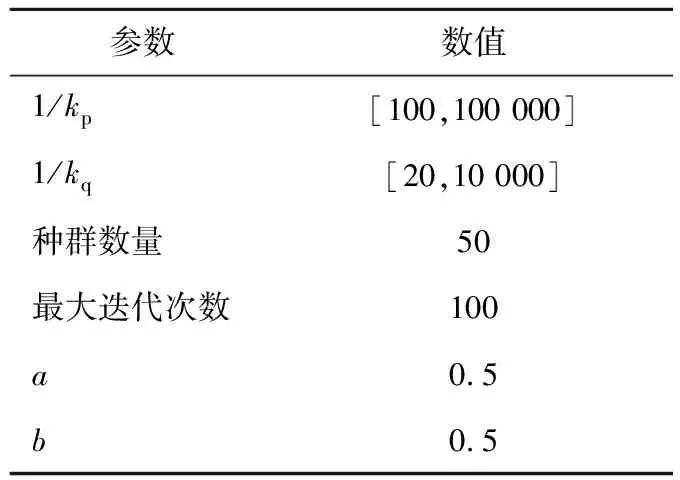
4.2 改进粒子群优化仿真
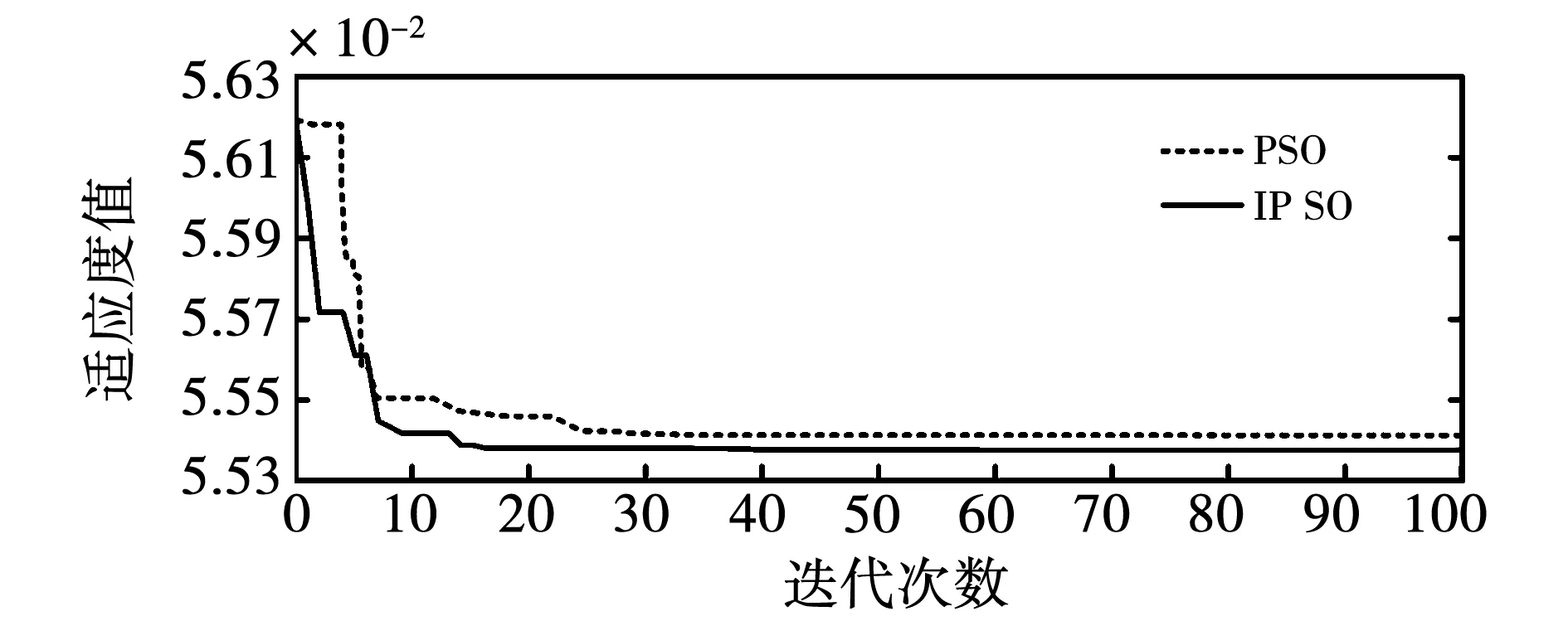
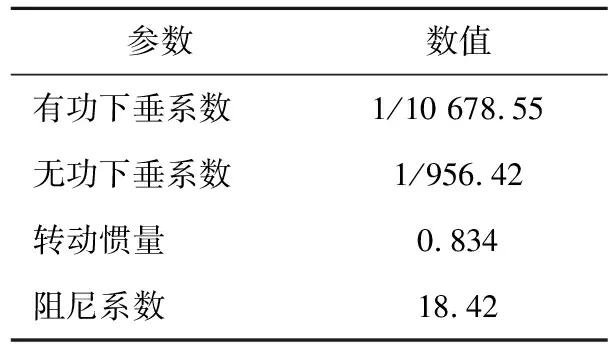
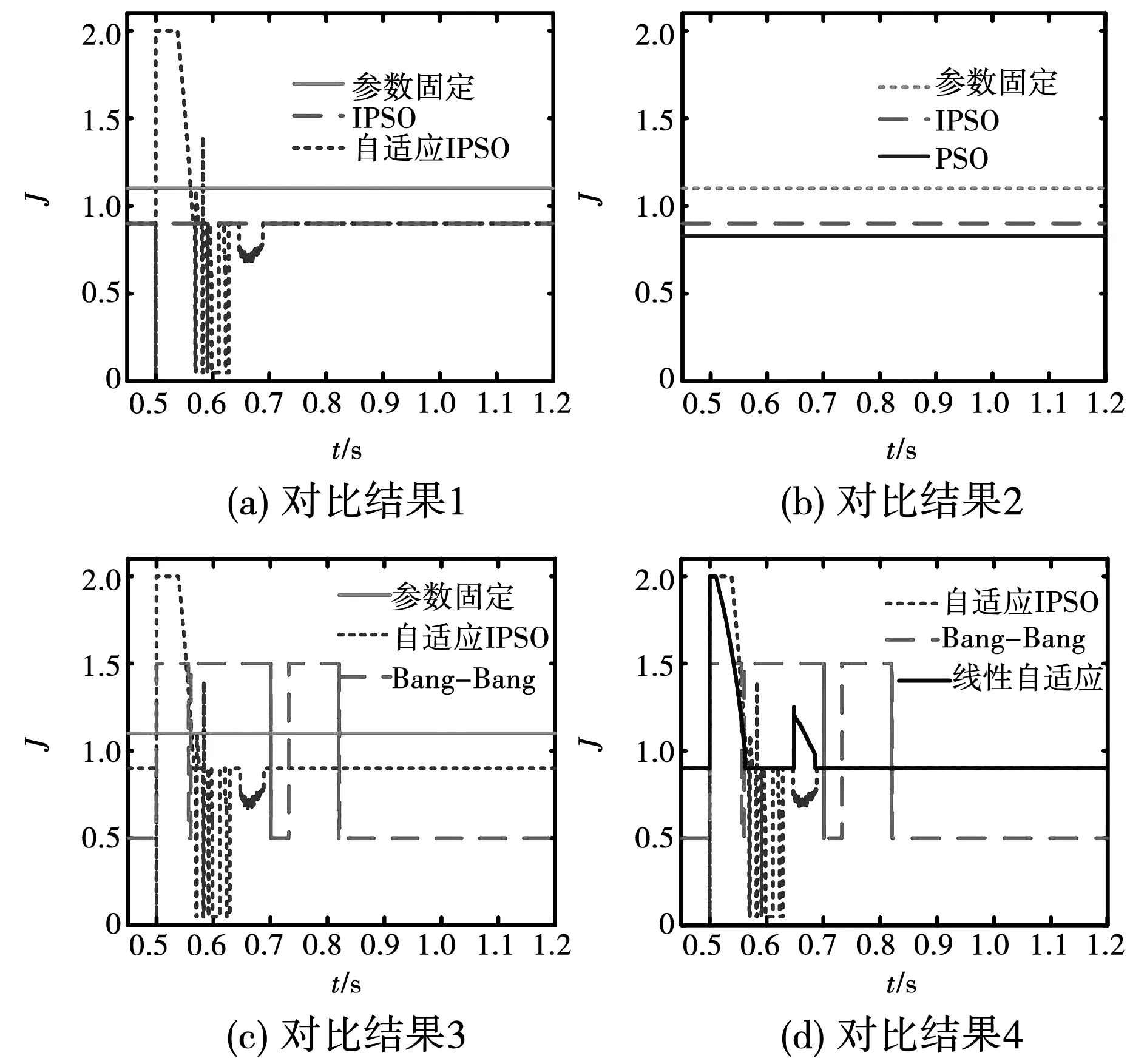
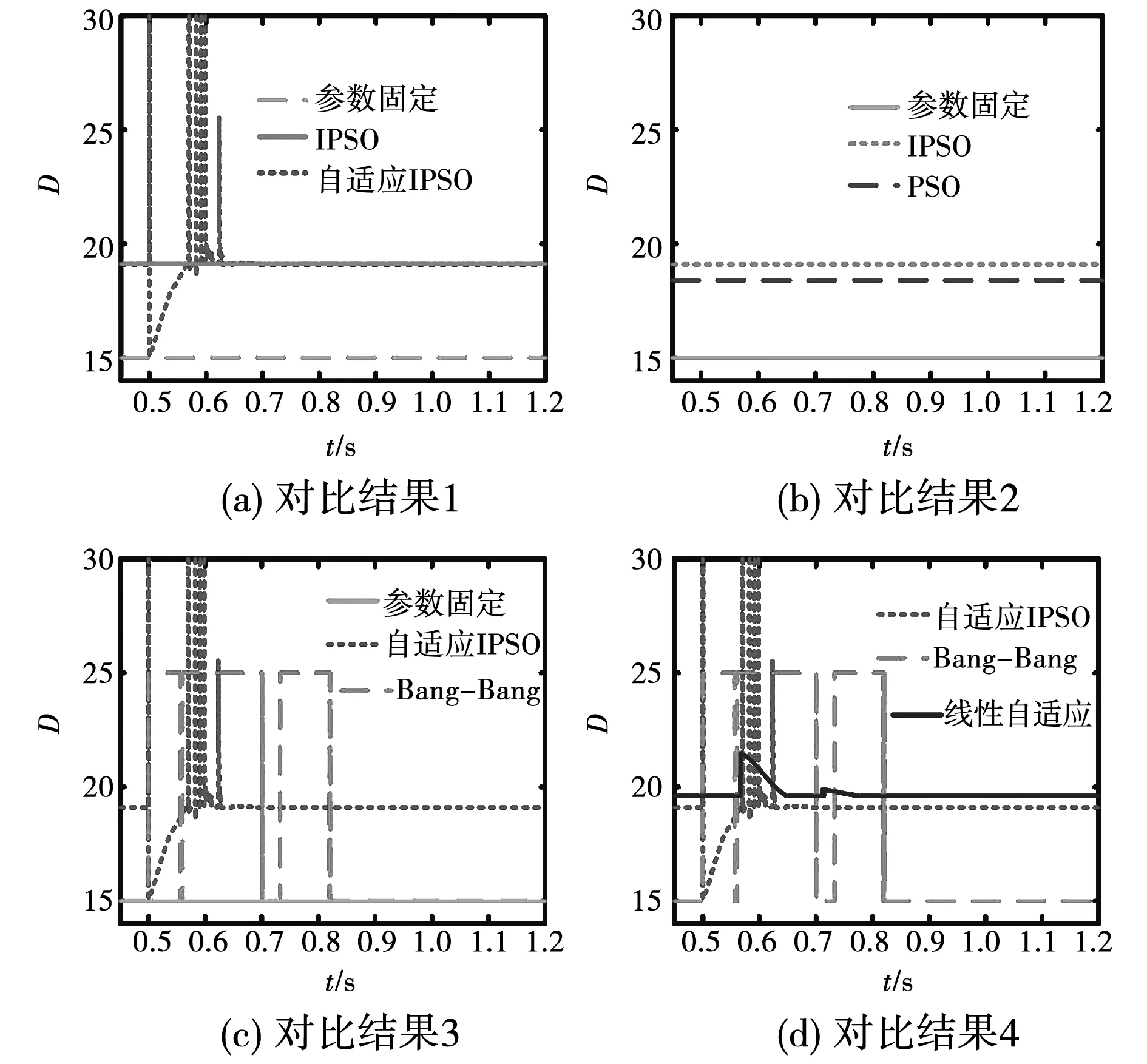
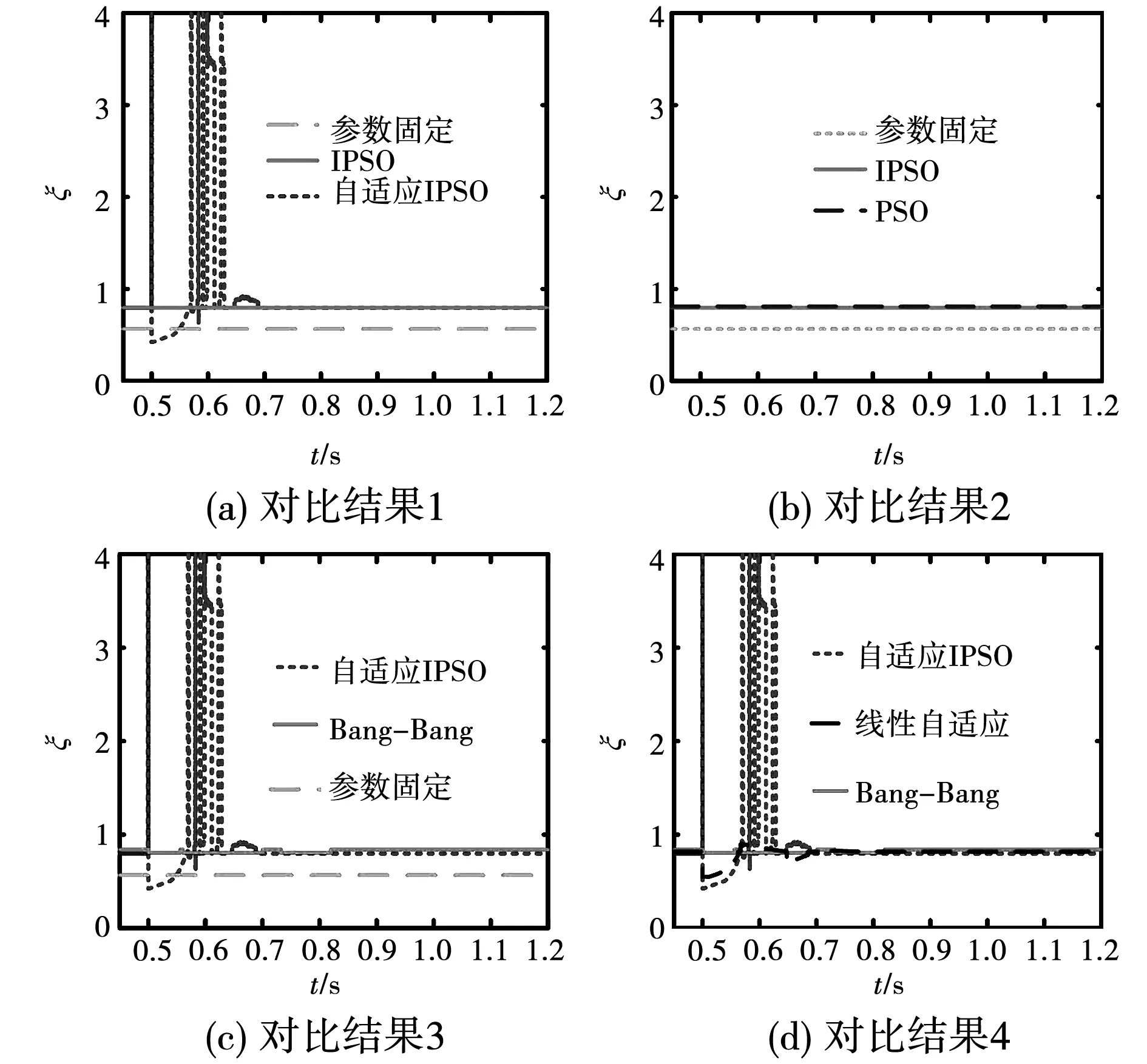
4.3 仿真结果对比


5 结 论
