基于UKF数据融合的勘测机器人定位方法
2022-07-15徐萌孔令华
徐萌, 孔令华
(1.福建工程学院机械与汽车工程学院,福州 350118;2.数字福建工业制造物联网实验室,福州 350118)
0 引言
在过去的20年中,对隧道、城市地下管廊、复杂洞穴环境等各类地下环境进行自主探索需求不断增长。具备自主定位导航功能机器人可应用于矿洞搜索救援、灾难响应及基础设施监测等领域[1]。由于卫星导航系统无法在地下正常工作,传统的IMU及里程计等传感器在长时间工作后会出现累计误差。因此必须提出一种能够提高移动机器人定位精度的导航方案。
目前,基于UWB(ultra-wideband)的定位系统最高定位精度可以达到厘米级[2]。其具有良好的信号隐蔽性、极低功耗、抗干扰能力强等特点,在室内定位中受到了越来越多的关注[3]。由于UWB属于超高频段,只适合视距传播条件,存在障碍物阻挡时,其测距精度会大打折扣。因此在复杂环境中仅使用某一种传感器很难在长时间内维持较高精度定位。众多学者开始研究UWB与其他传感器相结合的导航方法。例如,Zhang R. G.等[4]介绍了一种利用UWB、IMU、GNSS结合的室内外定位系统,可有效防止进出室内时丢失信号带来的影响;文献[5]中提出了基于卷积神经网络(CNN)的超宽带组合导航方法,可有效减小NLOS误差影响。文献[6]中利用2个UWB传感器及陀螺仪测量室内无人飞艇的姿态,并使用扩展卡尔曼滤波融合姿态信息,实现UAV自主导航;A. Marquez等[7]提出了利用IMU及UWB的传感器融合算法,实现精确的位置估计,提高了鲁棒性;Zhang W.等[8]设计了基于UWB与惯性测量单元的粮仓机器人定位系统,弥补了UWB传感器定位刷新频率低的问题,突破了对运动速度的限制,提高了定位精度。
本文采用UWB定位及IMU、里程计等传感器相结合的方式,通过UWB定位标签测量机器人位姿,与来自IMU及里程计的航向角及推算的位置信息,利用无迹卡尔曼滤波法做融合处理,得到了更为精确的航向角及位姿。该方法有效减少了UWB传感器因刷新频率低出现的数据延迟及里程计因随机漂移出现的累计误差。解决了在地下环境下无法准确获取航向及位置信息的问题,为勘测机器人实现高精度定位及导航提供了帮助。
1 多传感器定位系统
针对地下管廊、人防工程等需要定期巡检的地下工程,设计一种多传感器定位系统,如图1所示。该系统由SSMR(skid-steering mobile robot)四轮驱动移动机器人、UWB定位系统、计算终端组成。SSMR上装备IMU、里程计、定位标签传感器。可根据使用场景的范围大小配置不同数量的定位基站,其中最小定位系统应该至少由U0、U1、U2、U3四个定位基站组成。
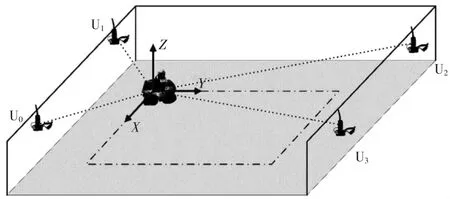
图1 地下空间定位系统
1.1 SSMR里程计定位
本文中使用的SSMR移动机器人,通过4台电动机驱动,并通过编码器获取位姿信息。该型机器人运动学示意图如图2所示。假设机器人几何中心与质心重合,以质心COG为原点建立机器人参考坐标系(x,y,z)。对机器人在世界坐标系(X,Y,Z)下水平运动进行分析。设机器人在COG坐标原点速度为v=[vx,vy,ωz]T。SSMR机器人相对世界坐标系状态方程为q=[X,Y,θ]T,其中X和Y代表COG点在世界坐标系中的坐标,θ为机器人参考坐标系X轴与世界坐标系X轴之间夹角,即机器人航向角。因此机器人在世界坐标系下的速度为q=[X˙,Y˙,θ˙]T。

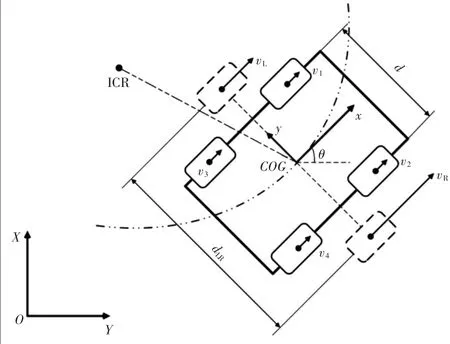
图2 SSMR移动机器人运动学示意图
SSMR移动机器人在转弯时,通过控制同侧轮速相同实现围绕ICR为圆心的运动,其实质为两侧转速不同的差速运动。参考文献[9]中的方法对四轮驱动机器人进行等效简化。则四轮驱动移动机器人简化为虚拟左右驱动轮的二轮差速运动,其中虚拟左右驱动轮速分别为vL、vR。vi(i=1,2,3,4)为实际驱动轮速度。转弯时同侧轮速相同,即满足式(2):

基于虚拟左右驱动轮速简化正运动模型可表示为
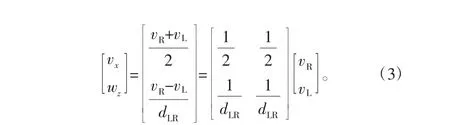
由式(1)、式(3)可以求出△t时刻SSMR机器人状态q=[X,Y,θ]T。如图3所示中(Xn,Yn,θn)为若干△t时间后的机器人状态,通过式(4)可计算机器人相对于初始状态的位姿。

图3 机器人轨迹推算

1.2 UKF数据融合算法
机器人里程计由位姿增量积分得到,工作精度高但存在累计误差。而超宽带传感器可以提供全局定位。二者相互融合可以弥补里程计存在累计误差的缺陷,提高定位系统鲁棒性。
由SSMR机器人轨迹推算模型可知该系统为非线性系统。针对非线性系统,无迹卡尔曼滤波(Unscented Kalman Filter,UKF)、扩展卡尔曼滤波(Extended Kalman Filter,EKF)均可解决非线性滤波问题。EKF算法对系统非线性部分进行一阶Taylor级数展开,这样线性化处理不可避免模型误差,同时会增加系统计算复杂度与成本[10]。而UKF则通过无迹变换UT(Unscented Transform)来得到非线性变换后的的概率分布。即对随机变量按分布进行sigma点采样,对采样点进行非线性变换以后获得后验分布。因此该算法可有效解决EKF算法估计精度低、稳定性差的问题[11]。
假设SSMR机器人以恒定线速度及角速度在二维平面上运动。以里程计测量信息作为系统输入,以UWB定位数据作为系统观测,将两种数据进行滤波融合。系统状态变量Xk=(x,y,θ)T定义为k时刻机器人在世界坐标系位姿。Zk=(x,y)T作为k时刻观测量。

式中:F及H分别为状态转移函数及观测函数;ωk为系统噪声,ωk~N(0,Q);vk为量测噪声,vk~N(0,R)。

UKF算法中步骤1)完成系统初始化,步骤2)、3)根据SSMR运动学模型,由上一时刻状态预测当前时刻状态。步骤4)利用传感器测量数据对预测值进行更新,得到最优状态估计。多传感器数据滤波融合的过程就是步骤2)、3)、4)的反复迭代[12]。
2 实验及结果分析
首先选择在实训中心大厅走廊搭建定位系统,该处处于室内,空间宽阔,适合模拟城市地下管廊等环境。遥控勘检机器人沿矩形路线一周,并在ROS操作环境中通过bag形式记录数据。
2.1 实验平台
本文采用的机器人为自主研发越野轮式移动机器人。采用四轮驱动、差速转向驱动方式。机器人上位机采用英特尔NUC(I5处理器),并装有ROS操作系统,下位机使用Pixhawk控制器,如图4所示。

图4 轮式勘检机器人平台
UWB定位系统选用Nooploop公司型号为LinkTrack定位、测距、数传一体化模块。内嵌三轴陀螺仪、三轴加速度计。测距、定位频率为200 Hz。定位范围为80 m,二维定位精度为10 cm。
2.2 实验设置
实验区域长宽约 为29.5 m ×12.5 m,如图5所示。在该实验环境中按长宽29.5 m×9 m矩形设置4部定位基站,并分别命名为U0、U1、U2、U3。机器人以初始位置作为原点,运动轨迹沿(0,0)、(9,0)、(9,22.5)、(0,22.5)坐标运行一周。其中可能遮挡UWB信号的为中间镂空护栏。
2.3 定位精度
以勘测巡检机器人初始位置为坐标原点,机器人在实验区域,沿着矩形轨迹绕场一周,并最终回到原点。通过不同传感器定位方法得到的轨迹如图6所示。从图中可以看出,仅使用里程计定位时,定位轨迹比较平滑,但是随着时间变化机器人在第一个转弯处航向估计就发生了较大的偏差,导致机器人位姿估计发生漂移,整个运动轨迹无法形成闭环。使用里程计与惯导结合定位,该方法可以通过惯导估计航向,弥补里程计因机器人打滑所产生的航向累计误差。使用超宽带定位修正里程计定位方法,该方法不仅可以避免航向估计误差,更可以通过全局定位减少里程计累计误差。由图中可以直观看出两种方法均能实现轨迹回环。
如图6所示,由图中可以看出机器人里程计定位在运行到25 s左右经过第一个转弯点便出现偏差,并且在X 轴方向上的偏差随时间推移而增大。
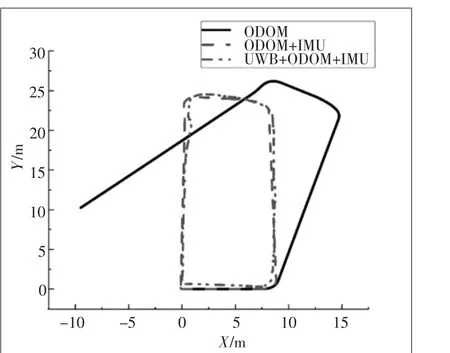
图6 定位轨迹图
图7、图8分别为X 轴方向定位误差及Y 轴方向定位误差,由图中可以看出本文所提出的UWB组合定位方法相比于里程计定位具有更高的定位精度

图7 X轴定位误差箱图

图8 Y轴定位误差箱图
由表1中数据分析可知,在位置估计上里程计定位误差约为4.4629 m, 而里程计惯导融合定位及超宽带融合定位均能达到厘米级定位,其中超宽带融合定位比里程计惯导定位精度提升40%,且方差值更小,具有鲁棒性。
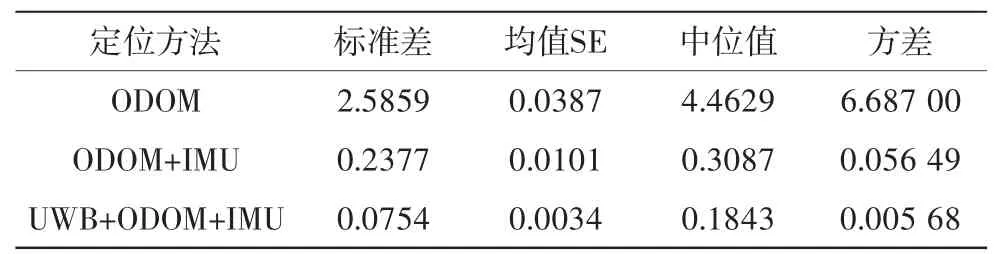
表1 各定位方法精度 m
3 结论
实验结果表明,机器人在29.5 m×12.5 m的无GPS环境中作业时,定位误差可达到厘米级。所提出的UKF融合滤波算法定位算法相对于单独使用里程计定位精度有一定的提升。在地下空间等缺少GPS高精度导航环境下,该方法可有效提高勘测机器人定位精度,实现机器人在地下环境的自主导航。
