座舱盖骨架危险薄弱部位可靠性分析研究
2022-07-15邱蕾蕾王雪许光群谢金标
邱蕾蕾,王雪,许光群,谢金标
(国营芜湖机械厂,安徽 芜湖 241007)
0 引言
某型飞机活动座舱盖主要由前中后弧框、侧骨架、通条压板和有机玻璃组成[1],主要作用是为飞行员进出座舱盖提供通道及良好的飞行视野,同时在飞行中保护飞行员免受外界气流的影响[2-3]。飞机在服役过程中不仅要承受各种循环加载载荷,同时还需抵挡外来物(如鸟撞等)带来的冲击力[4],这些性能要求座舱盖结构有足够的强度来满足飞行安全。
经外场使用统计,飞机在飞行过程中座舱盖骨架侧型材、前弧支臂及中弧拉杆处等部位裂纹故障的发生概率较高,属于危险薄弱部位,裂纹的扩展对飞行安全产生较大的影响。针对裂纹扩展规律,Sih[5]和Hartranft[6]研究了复变量方法,结果表明裂纹的强度因子与型材的厚度有着极大的关联;对于板材在受到拉伸和弯曲载荷时,裂纹失稳后延续扩展准则,Wynn等[7]进行深入研究,结果表明“能量型”准则与实际情况更加吻合;Lanciotti等[8]对铝合金材质的贯穿性裂纹在拉伸和弯曲应力共同作用下的扩展速率进行了研究,结果表明裂纹扩展速率与拉伸与弯曲应力的占比有关。
本文针对座舱盖骨架侧型材危险薄弱部位进行了损伤容限分析,主要包括未修理下侧型材损伤容限、采用1 mm厚钢板加强后侧型材损伤容限,以及1.5 mm厚钢板加强后侧型材损伤容限。研究结果表明,采用钢板加强后,座舱盖骨架侧型材使用可靠性得到了极大的提升。
1 典型危险薄弱部位介绍
某座舱盖侧型材骨架通过多个锁环与机身上的锁钩相连将座舱盖固定到前机身上,经过座舱盖静力疲劳试验和外场服役期间故障数据统计,发现座舱盖锁环处侧型材出现凹坑、裂纹(如图1)。其主要原因为锁钩受载状态受锁钩与锁环的间隙影响,同时第4把锁钩结构不同于其它锁钩,而左右两侧锁环结构形式均相同,静力试验显示第4把锁环在飞行过程中所承受的载荷最大。

图1 某型机座舱盖锁环处凹坑
2 危险薄弱部位有限元建模
基于ABAQUS有限元软件建立图2所示的有限元模型,分别建立以下3种表示不同工况的模型:修理前不含钢板,修理后钢板厚度分别为1 mm和1.5 mm。
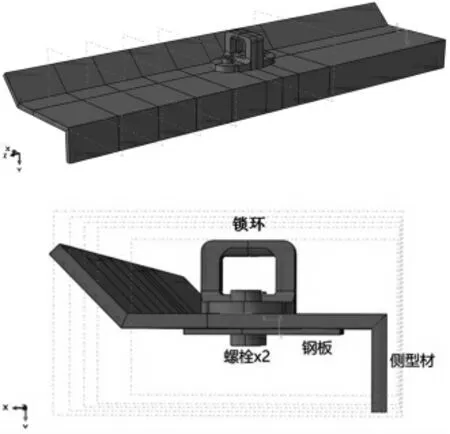
图2 有限元建立的侧型材与锁环结构示意图
其中侧型材的材料为铝合金,力学性能参数为:密度为2700 kg/m3,弹性模量为70 GPa,泊松比为0.33。锁环、螺栓及钢板的材料为钢,力学性能参数为:密度为7800 kg/m3,弹性模量为202 GPa,泊松比为0.3。
网格划分如图3所示,对于锁环采用C3D10网格类型,对于侧型材、螺栓、钢板采用C3D8网格类型。

图3 锁环、螺栓、钢板和侧型材的划分网格示意图
载荷条件和边界条件如图4所示,载荷施加在锁环内侧,沿离面方向(图中-y方向)大小为20 549 N,沿指向舱内方向(图中-x方向)大小为3358 N,对两侧如图所示位置进行固支约束。
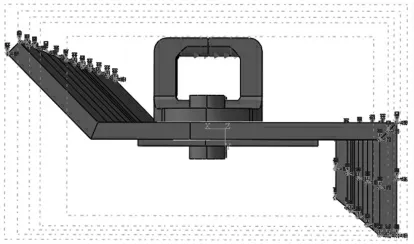
图4 ABAQUS中施加载荷与边界条件
3 有限元计算结果
考虑锁环、锁钩由于接触间隙不均匀而造成的载荷分散性,参考静力试验中所测锁环和锁钩上的试验数据,将用于侧型材与锁环连接孔损伤容限分析的载荷谱按一定比例加重,设定初始裂纹设置为穿透裂纹3 mm。
3.1 修理前计算结果
修理前,整体结构的Mises应力云图如图5所示,最大应力位于侧型材孔边。为方便按照图6所示的相邻孔边裂纹模型计算,即侧型材与锁环连接孔为有限大板相邻孔边裂纹,受钉传载荷、远端(参考界面)弯矩和均匀拉应力作用。结构尺寸分别为:两孔之间距离为26 mm;板厚t=3 mm;孔径D=6.2 mm。选取S11方向观察其载荷分布情况。
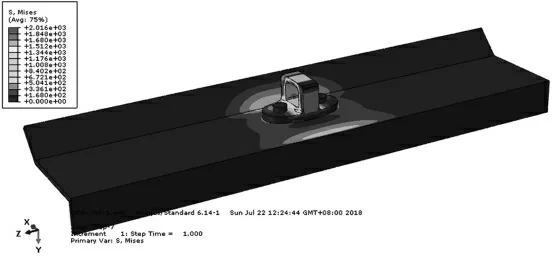
图5 结构Mises应力云图
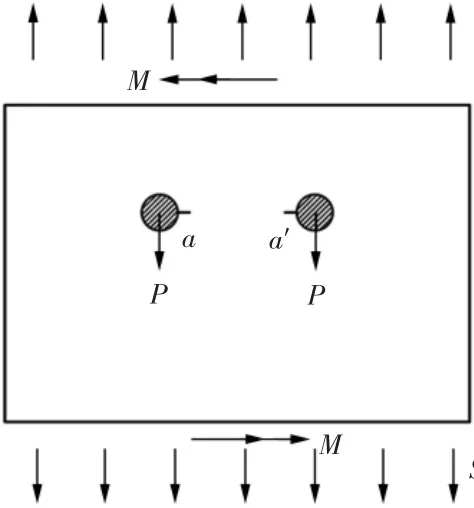
图6 相邻孔边裂纹
如图7所示,在板的远端应力较小,应力主要集中于孔边,并且在孔边上下表面受力明显不同,上表面最大应力为拉应力,下表面为压应力,上下表面间存在弯矩,故在计算时应考虑弯矩的影响。
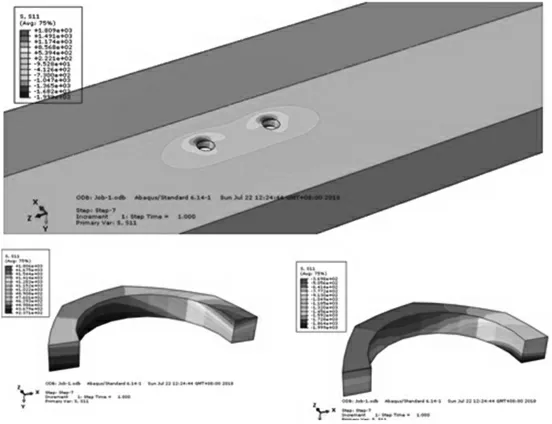
图7 侧型材及上下孔边S11应力云图
3.2 修理后加1 mm厚钢板计算结果
结构Mises应力云图如图8所示。侧型材及上下孔边S11应力云图如图9所示。
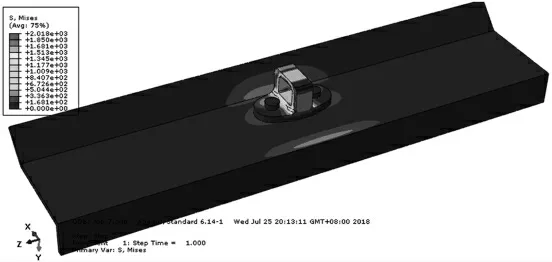
图8 结构Mises应力云图
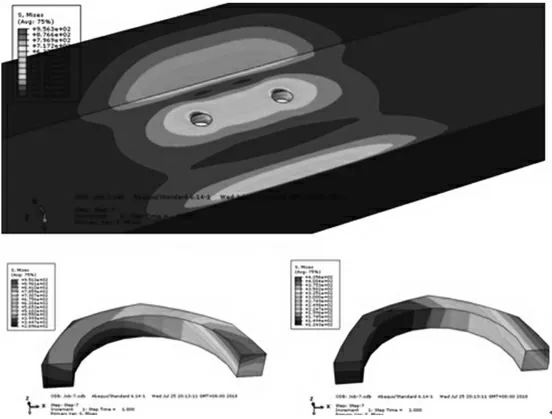
图9 侧型材及上下孔边S11应力云图
3.3 修理后加1.5 mm厚钢板计算结果
结构Mises应力云图如图10所示。侧型材及上下孔边S11应力云图如图11所示。
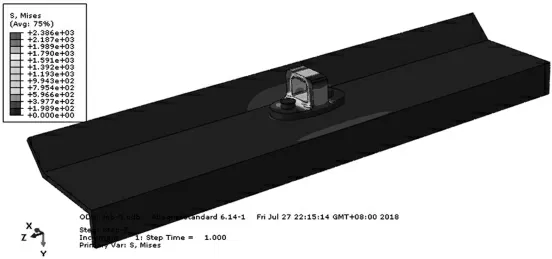
图10 结构Mises应力云图
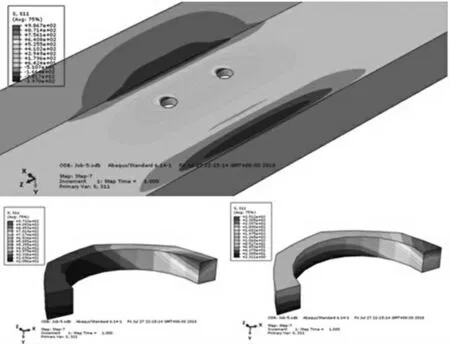
图11 侧型材及上下孔边S11应力云图
3.4 弯矩和钉传载荷
如图12所示,首先计算了Py和Pz载荷对螺栓处的弯矩(如图12(a)),然后简化侧型材与锁环为一对边简支矩形薄板在集中载荷作用下的弯矩模型(如图12(b)),最后分别计算侧型材两个螺栓孔处的弯矩(如图12(c))。
1)计算锁环上Py和Pz载荷对螺栓的弯矩(如图12(a))。Pz载荷与螺栓间的弯矩可简化为悬臂梁,此处Pz=3358 N,L=12.5 mm。Pz载荷与螺栓间的弯矩MPz=Pz×L=41975 N·mm;同理,可以计算Py载荷与螺栓间的弯矩,其中离心Py载荷与销钉之间距离为1.5 mm。此处分别计算两种不同Py值的情况:若Py=20549 N,弯矩M-Py=20549×1.5=30823.5 N·mm,其方向与M-Pz相反,故载荷对于螺栓连线的弯矩M螺栓=41975-30823.5=11151.5 N·mm;若Py=13000 N,弯矩M-Py=13000×1.5=19500 N·mm,M螺栓=41975-19500=22475 N·mm。
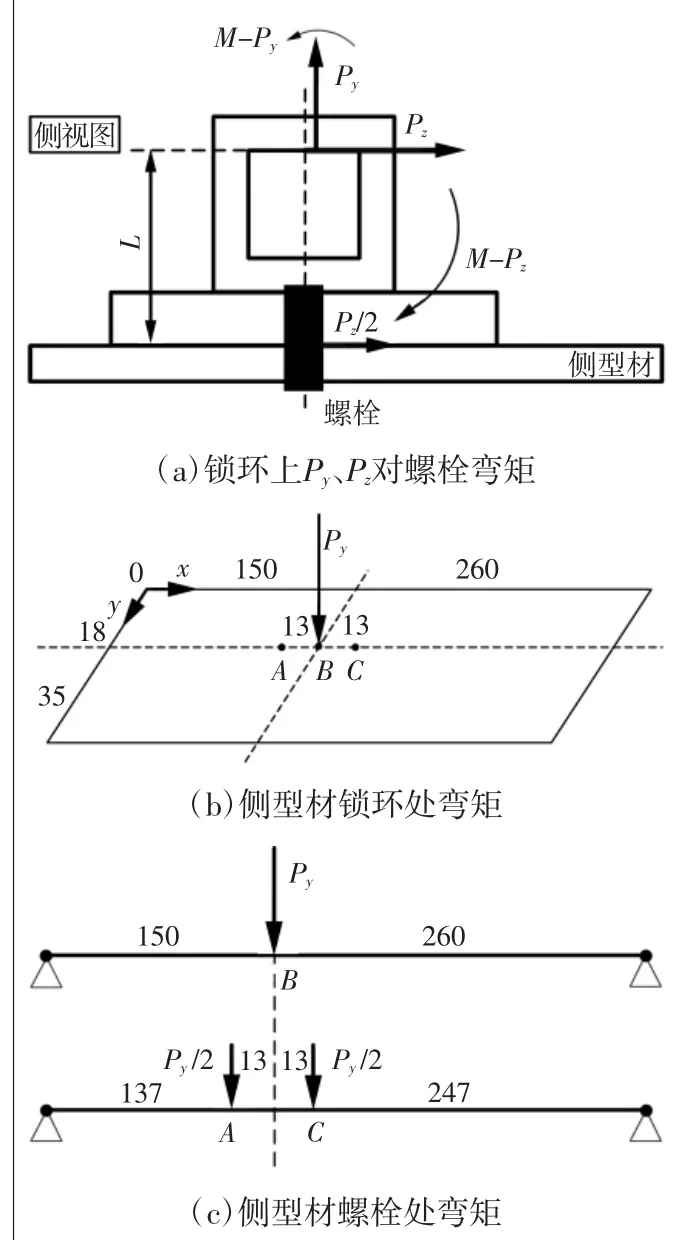
图12 弯矩计算过程示意图
2)计算锁环当量集中力,计算锁环处弯矩,如图12(b)所示,四边简支板,与板的尺寸相比,两螺栓孔间距可忽略不计,认为B点为载荷Py作用点,若载荷Py=20549 N,根据弹性力学计算得到B点处的弯矩Mx=483114.68 N·mm;若载荷Py=13000 N,根据弹性力学计算得到B点处的弯矩Mx=305634.86 N·mm。
3)分别计算侧型材两个螺栓孔处的弯矩。如图12(c)所示,将载荷等效为在两个螺栓处,即将B点载荷等效到A和C。Py=20549 N时,A点弯矩MA=483114.68×137÷150=441244.743 N·mm,C 点弯矩MC=483114.68×247÷260=458958.948 N·mm;Py=13000 N时,A点弯矩MA=305634.86×137÷150=279146.50 N·mm,C点弯矩MC=305634.86×247÷260=290353.117 N·mm。
最后,分别计算两个螺栓处的最终弯矩,即平板内A、C各个点的弯矩加上螺栓处弯矩,即MA总=MA+M螺栓。Py=20549 N时,A点弯矩MA总=452396.243 N·mm,C点弯矩MC总=483114.68×247÷260=470110.448 N·mm;Py=13000 N时,A点弯矩MA总=301621.5 N·mm,C点弯矩MC总=312828.117 N·mm。可以看出,针对不同的Py值,均显示C点弯矩略大于A点。
此外,由于存在2个螺栓,故单个螺栓上的钉传载荷P=Pz/2=1679 N。
4 损伤容限分析
4.1 计算模型
裂纹类型为有限大板相邻孔边裂纹,受钉传载荷、远端(参考界面)弯矩和均匀拉应力作用。此处采用其1/2模型进行计算分析,如图13所示。
如图13所示,尺寸分别为:W=260 mm(取锁环至最后端面距离,图12中C点距离);W=150 mm(图12中A点距离);B=13 mm;D=6.2 mm。
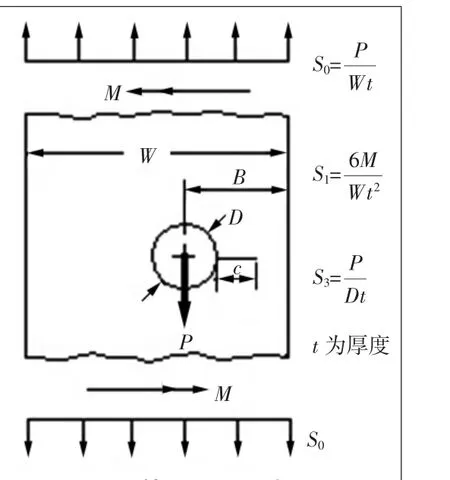
图13 计算模型示意图(1/2模型):穿透裂纹
4.2 材料属性
此处计算所采用材料为2系铝合金包铝板材,屈服强度σy=340 MPa,抗拉强度σb=452 MPa,其在高温(150 ℃)下L-T 方向的裂纹扩展速率曲线如图14所示。
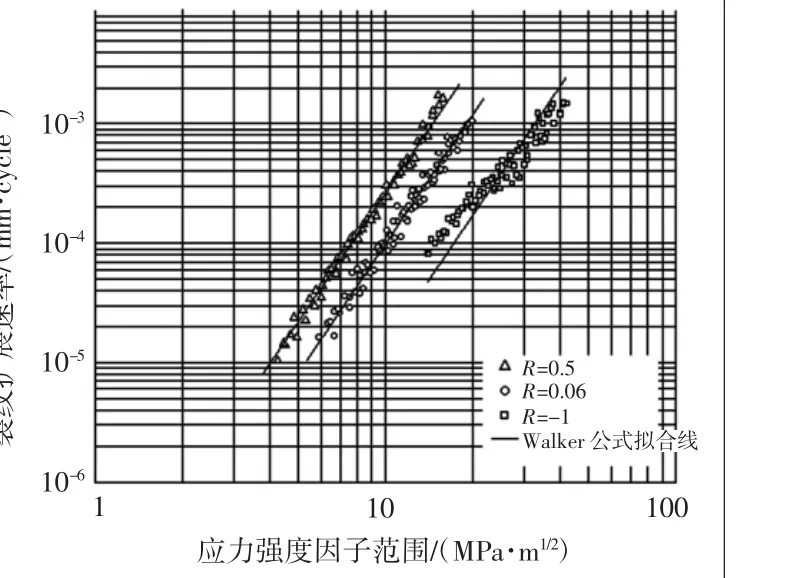
图14 2系铝合金包铝板材L-T方向高温da/dNΔK数据及Walker公式拟合线
采用Walker公式拟合:

相关参数具体拟合值为:C=2.209×10-8;n=3.60;M1=0.56(R≥0)。
4.3 施加载荷
结合图13所示的计算模型,对于不同的工况,等效载荷计算公式为:
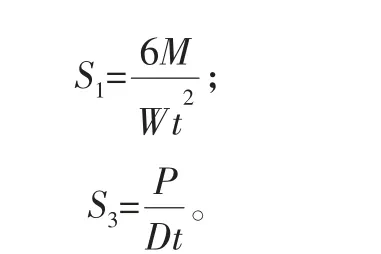
式中,宽度W按照完整模型宽度计算,W=410 mm。
有限元计算结果显示在距离孔的远端,拉伸应力非常小,近似等于0,这是由于边界约束的存在,所以此处计算时取S0=0 MPa,对修理后的情形亦同。
4.4 失效准则
1)临界K准则。Kmax超过断裂韧度Kc,t=3 mm,Kc=67.64。
2)净截面屈服准则(NSY准则)。
3)两侧裂纹尖端塑性区重叠连通,此处采用基于Irwin公式的循环塑性公式来计算:
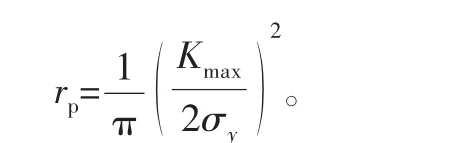
4.5 计算结果
4.5.1 修理前计算结果
此处分为4种情况,分别计算Py=20549 N、Py=13000 N时在W=260 mm(C点)和W=150 mm(A点)处对应的裂纹扩展寿命,然后取最危险情况进行后续分析。
1)第一种情况:Py=20549 N,W=260 mm。
S1=764.407 MPa,S3=90.268 MPa,失效方式为两侧裂尖塑性区重叠连通,临界裂纹长度为9.07 mm,最大应力强度因子Kmax=52.07,对应两侧裂纹扩展剩余长度为0.93 mm,计算临界裂纹长度循环塑性区长度rp=1.86 mm,一半即为0.93 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。计算结果为:经历总循环数为857,等效飞行小时为1045.80 h。
2)第二种情况:Py=13000 N,W=260 mm。
S1=508.664 MPa,S3=90.268 MPa,失效方式为两侧裂尖塑性区重叠连通,临界裂纹长度为9.40 mm,最大应力强度因子Kmax=41.77,对应两侧裂纹扩展剩余长度为0.60 mm,计算临界裂纹长度循环塑性区长度rp=1.20 mm,一半即为0.60 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。计算结果:经历总循环数为3625;等效飞行小时为4462.52 h。
3)第三种情况:Py=20549 N,W=150 mm。
S1=735.604 MPa,S3=90.268 MPa;失效方式为两侧裂尖塑性区重叠连通,临界裂纹长度为9.105 mm,最大应力强度因子Kmax=50.90,对应两侧裂纹扩展剩余长度为0.895 mm,计算临界裂纹长度循环塑性区长度rp=1.784 mm,一半即为0.892 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。计算结果:经历总循环数为956,等效飞行小时为1170.70 h。
4)第四种情况:Py=13000 N,W=150 mm。
S1=490.441 MPa,S3=90.268 MPa,失效方式为两侧裂尖塑性区重叠连通,临界裂纹长度为9.42 mm,最大应力强度因子Kmax=40.87,对应两侧裂纹扩展剩余长度为0.58 mm,计算临界裂纹长度循环塑性区长度rp=1.15 mm,一半即为0.58 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。计算结果:经历总循环数为3950,等效飞行小时为4871.32 h。
可以看出在Py=20549 N、W=260 mm时,裂纹扩展寿命是最短的,故修理后均基于此固定参数进行分析。
给出修理前Py=20549 N、W=260 mm时的裂纹长度与飞行小时关系,如图15所示。
剩余强度与裂纹长度关系如图16所示。
4.5.2 修理后加1 mm厚钢板计算结果
失效方式为两侧裂尖塑性区重叠连通,临界裂纹长度为9.50 mm;最大应力强度因子Kmax=38.47,对应两侧裂纹扩展剩余长度为0.50 mm,计算临界裂纹长度循环塑性区长度rp=1.01 mm,一半即为0.50 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。经历总循环数为6838;等效飞行小时为8419.44 h。裂纹长度与飞行小时关系如图17所示。剩余强度与裂纹长度关系如图18所示。
4.5.3 修理后加1.5 mm厚钢板
失效方式为两侧裂尖塑性区重叠连通;临界裂纹长为9.59 mm,最大应力强度因子Kmax=34.08,对应两侧裂纹扩展剩余长度为0.41 mm,计算临界裂纹长度循环塑性区长度rp=0.80 mm,一半即为0.40 mm。可以保证剩余裂纹可扩展长度即为两侧裂纹尖端塑性区重叠时的长度。经历总循环数为15 720;等效飞行小时为19 356.20 h。裂纹长度与飞行小时关系如图19所示。剩余强度与裂纹长度关系如图20所示。
初始计算的裂纹扩展寿命按照分散系数2进行折算,计算结果如表1所示。

表1 侧型材与锁环连接孔裂纹扩展寿命(飞行小时) h
5 结论
座舱盖骨架侧型材修理后加1 mm和1.5 mm厚钢板后,孔边应力明显减小,采用1 mm钢板加强后寿命比原始提高了约8倍,1.5 mm钢板提高了约17倍,大大提高了座舱盖危险薄弱部位使用的可靠性,降低了座舱盖外场使用的风险,进一步保障了飞行员的生命安全。

图15 裂纹长度-飞行小时曲线图

图16 剩余强度-裂纹长度关系图

图17 裂纹长度-飞行小时曲线图

图18 剩余强度-裂纹长度关系图
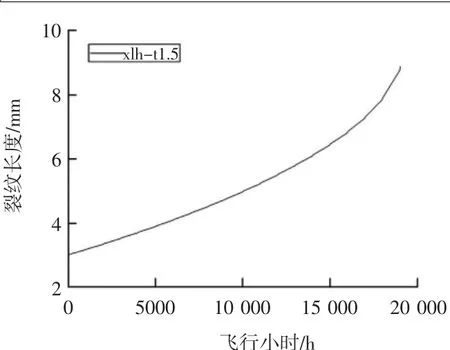
图19 裂纹长度-飞行小时曲线图
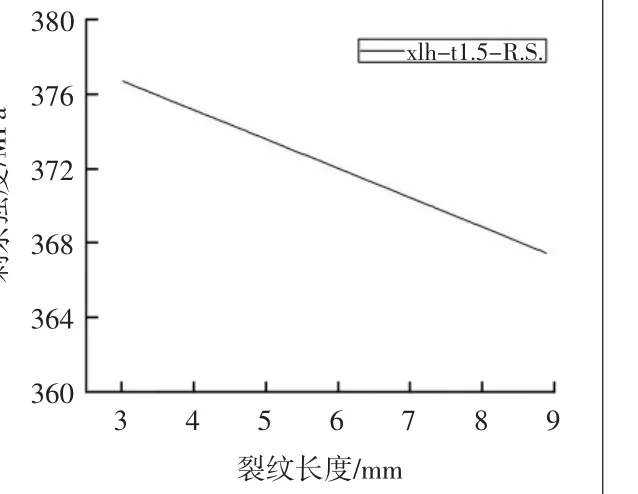
图20 剩余强度-裂纹长度关系图
