等效场变换理论及浅海声辐射计量

何 呈， 王 彪， 罗成名， 马 林， 李晓曼

(江苏科技大学 电子信息学院， 江苏 镇江 212000)

水下目标声辐射常用的计量方法分为两类：一类是直接测量法，它需要选择开阔水域，满足目标结构声辐射的远场条件，同时将水域处理成无边界的理想声介质，不考虑水域边界的声散射；另一类方法是间接测量法，通过获取目标结构表面的振动参数，结合声场格林函数，推算目标结构远场的辐射声。

受空间尺度的限制，目前常用的声辐射计量方法是一种间接测量技术——近场声全息技术(near-field acoustic holography, NAH)。该技术在20世纪80年代初由Maynard等[1-2]提出，使用放置在平板声源附近的共形麦克风阵列获得声场的复声压，重构出平板声源的振动参数。NAH自提出以来，在国内外声源辐射[3-7]、声散射测量[8]和声源识别[9-11]的研究中得到了广泛应用。

由于水下目标尺寸大、海洋广阔等因素，水下声场通常涉及很大的空间范围，在研究中非常关注声源的远场特性。自由场中的远场特性由于与测量环境无关，通常被用于声源声辐射特性的评判依据，显得尤为重要。暴雪梅等[12-14]采用声全息技术获得源面的声场，然后根据自由场中远场与源面的格林函数预测声源的远场声场。在此过程中，经历了两次声场估计：第一次是属于声学反问题求解，得到源面振动参数；第二次属于声学正问题，得到源面振动辐射声在远场的分布。

针对有限空间内的辐射声获取技术，孙超等[15]采用波叠加源算法(WSA)和Helmholtz方程最小二乘算法(HELS)的NAH，在有限空间内将混合声场进行分离得到声源在自由空间的辐射声场估计。Wall等[16]提出了一种多源统计优化近场声全息方法(M-SONAH)，M-SONAH可以在多源环境下重建目标近场声压，误差较小。宋玉来等[17-18]针对传声器阵列两侧存在相干声源的非自由声场重建问题，可以在非自由声场的测量条件下，有效去除干扰声的影响,实现目标声场的准确重建。Jin等[19]提出了一种只依赖全息面数据的直接声场分离方法，简化了分离位于全息面不同侧面的相干声源的过程，Bi等[20]利用该原理实现了目标入射声与散射声的分离。胡博等[21-22]采用矢量水听器来进行声全息重构，与传统声压水听器相比，降低了测量系统的复杂程度。

NAH本质上属于声场的逆问题，通过声源的辐射声场反向溯源，对声源的振动参数进行估计。NAH还需要准确的源面信息，用于构造源面与观测空间的格林函数。当声源结构间存在相互遮挡、源与全息面存在相对运动时，源面与全息面的声场格林函数复杂，涉及到复杂的动态多体散射问题[23]。

综上所述，目前声辐射直接计量法需要大空间范围以满足远场测试条件；有限空间中辐射声计量面临所需参数众多，需要精密的源面几何参数，辐射声场获取过程繁琐，存在声场逆问题求解等问题。针对空间辐射声场计量中面临的以上问题，本文提出了一种新的声辐射场估计理论——等效场变换(equivalent field transformation, EFT)理论。该理论无须源面几何信息，与声源的几何形状、材质、运动状态无关。当声源在目标空间内时，就能获得准确的目标声辐射结果；无须预先对源上振动参数进行估计，可直接得出声源在自由场远场或近场的声场，属于声场的正问题，求解上不存在不适定的问题；对测量环境没有限制，适用于非自由场环境。声散射本质上属于目标在入射声激励下的再辐射问题，该理论也适用于目标声散射的计量。

1 等效场变换理论

假设目标空间V0中存在一个体积声源，其任意点的辐射声压是ps(x0,y0,z0)，坐标点(x0,y0,z0)在空间V0内部，如图1所示。

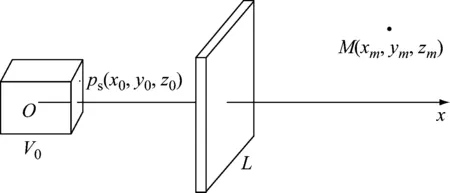
图1 空间区域对空间点变换Fig.1 The transformation form a region to a point (The observation results from point M can be predicted by the observation results of space L)

根据声波叠加原理，待测点M(xm,ym,zm)的声压为

(1)

式中，gM(x0,y0,z0)是V0中坐标点(x0,y0,z0)到M点的声场格林函数。

观测空间L上某一点(xl,yl,zl)的声压为

pL(xl,yl,zl)=

(2)

式中，gL(x0,y0,z0,xl,yl,zl)是空间V0中坐标点(x0,y0,z0)到空间L上坐标点(xl,yl,zl)的声场格林函数。

假设存在函数q(xl,yl,zl)，使得式(3)成立。

(3)

将式(1)、(2)代入式(3)得到

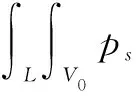
(4)

式(4)表明，对于空间V0中的任意一点(x0,y0,z0)，均满足式(5)。

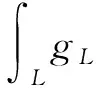
gM(x0,y0,z0),∀(x0,y0,z0)∈V0

(5)

在自由场环境下，空间点(x0,y0,z0)到M点的声场格林函数gM(x0,y0,z0)和点(x0,y0,z0)到观测空间L上坐标点(xl,yl,zl)的声场格林函数gL(x0,y0,z0)均可由点源的球面波扩展得到，gM和gL是已知量。将gM和gL代入式(5)即可解出函数q(xl,yl,zl)。

将观测空间L上的实测值pL(xl,yl,zl)与函数q(xl,yl,zl)代入式(3)，可求出M点的声压pM(xm,ym,zm)。当式(5)的解存在时，说明能够通过观测空间L中的观测数据直接获得M点的声场；反之则不能。

该方法使用声源外某一观测空间的观测值，经过声场变换获得声源在外场空间某一待测位置点的声场值，观测空间获取的结果与空间位置点的声场结果等效，称之为等效场变换(EFT)。EFT与近场声全息方法相比，不需要知道源面的几何形状，只需得出函数q(xl,yl,zl)即可通过声源观测空间L上观测值，直接获得目标空间V0中的任意声源在外空间某一位置或方向上的取值。

2 权系数函数q(xl,yl,zl)与声场分析

2.1 V0中声场分布与M点声场获取

gM(x0,y0,z0)是空间V0中的一点(x0,y0,z0)到M点的声场格林函数，根据声场互易原理，gM(x0,y0,z0)也可以被看作是M点到空间V0中的点(x0,y0,z0)的声场格林函数。因此，当M点为单位无指向性点源(声压为1，相位为0)时，格林gM(x0,y0,z0)在空间V0中的分布，与M点的点源辐射声在空间V0中的声压场分布一致。

假设测量空间L上使用收发合置换能器，式(3)表明，使用权系数q(xl,yl,zl)激发的声场与M点的单位点源辐射声在空间V0中的声场一致。由此可得出EFT理论的一条推论：

当空间L上的收发合置换能器在系数q(xl,yl,zl)的加权下，V0中的声场与M点无指向性单位点源激发的声场一致时，便可通过空间L上的观测值与权系数q(xl,yl,zl)获得空间V0中任意声源在M点的声场。

如图2所示，处于M点的单位无指向性点源在空间V0的声场为pM(x0,y0,z0)，(x0,y0,z0)∈V0。如图3所示，空间L上的收发合置换能器在空间V0的激发声场为pL(x0,y0,z0)，(x0,y0,z0)∈V0。假设L上的收发合置换能器在权函数q(xl,yl,zl)的作用下，激发的V0声场与M处单位点源激发的V0声场一致，如式(6)所示。

pM(x0,y0,z0)=pL(x0,y0,z0)，∀(x0,y0,z0)∈V0

(6)

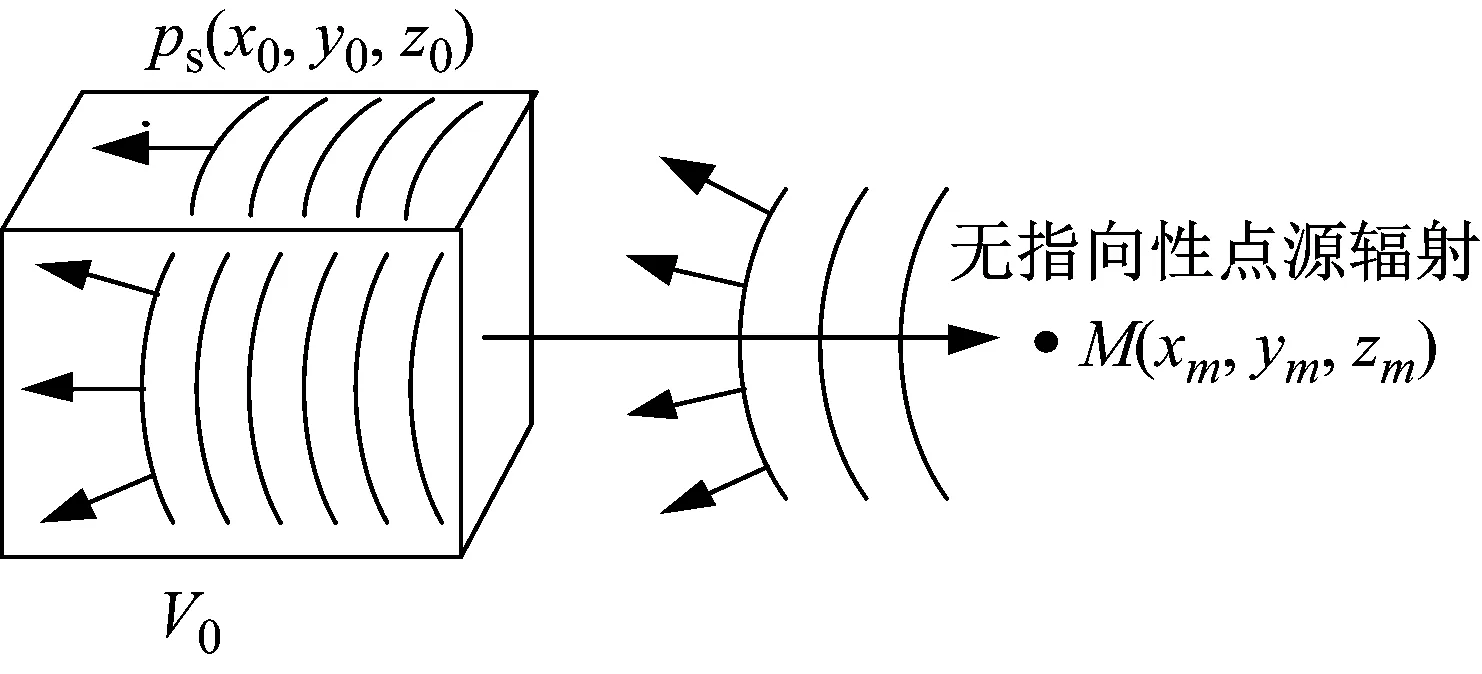
图2 M点无指向性声源在空间V0的声场Fig.2 The sound field in space V0 caused by unit omni-point source M

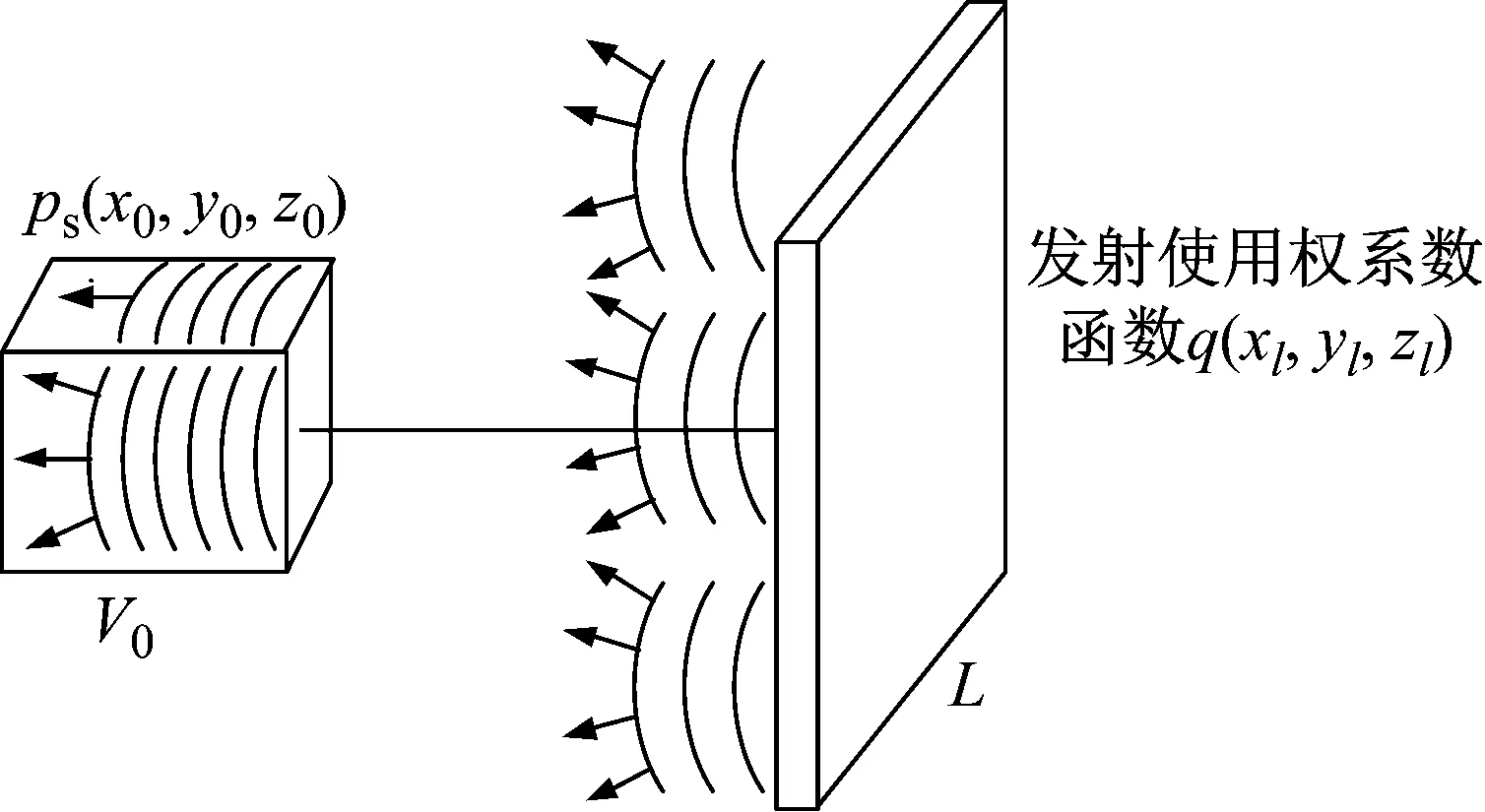
图3 声源L在函数q(xl,yl,zl)加权下的声场(V0中声场与图2中的一致)Fig.3 The sound field in space V0 caused by source L under the weighting function q(xl,yl,zl) (the sound field in V0 is consistent with that in Fig.2)

那么，当L上的收发合置换能器用于接收时，在权系数q(xl,yl,zl)作用下，就能够获得空间V0中任意声源在M点的声场取值，如图4所示。实现对观测空间V0到空间点M的声场变换。该变换方法与声源s0的内部结构、几何形状、材质、声源类型、指向性、以及运动状态均无关，只须声源处于空间V0内部，就能获得声源在外场M点的声场。

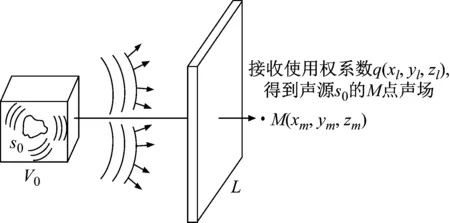
图4 空间V0中声源s0的近场辐射获取Fig.4 Obtain near-field sound radiation of source s0 in space V0

2.2 声源的远场指向性获取

当需要获得声源的远场特性时，理论上M点距离声源无穷远。M点的单位无指向性点源的辐射声在空间V0中的声压场分布为平面波，如图5所示。

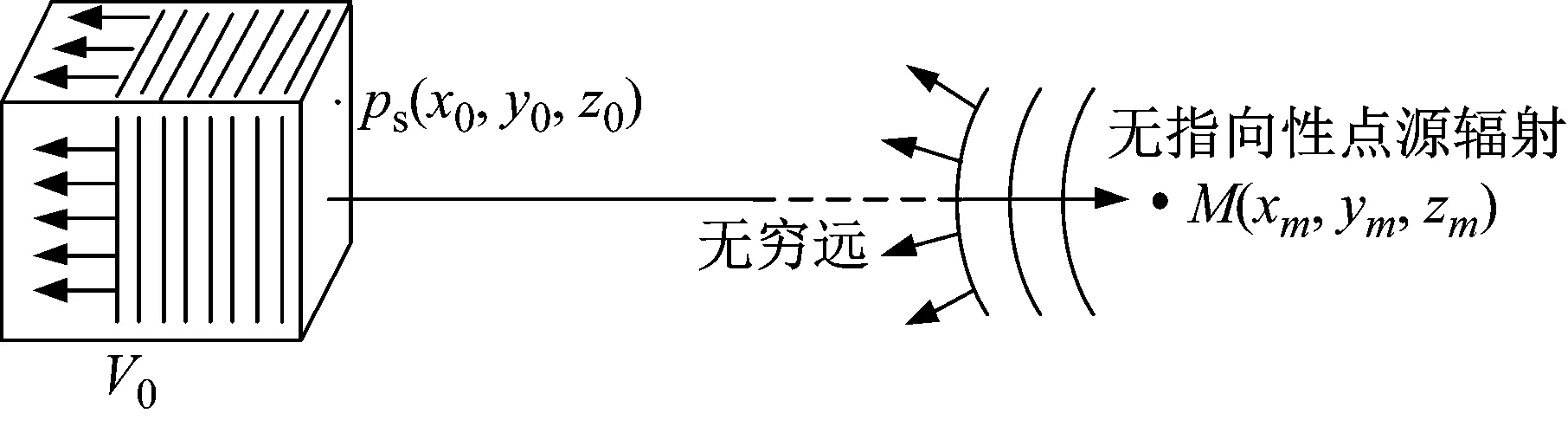
图5 空间V0中平面波Fig.5 Plane wave in space V0 from a unit omni-point-source at M which is far from V0

根据前面的推论可知，若空间L上的收发合置换能器能够在空间V0中激发平面波如图6所示。那么将发射时使用的加权函数q(xl,yl,zl)用于接收，就能够获得空间V0中任意声源的远场声场，如图7所示。

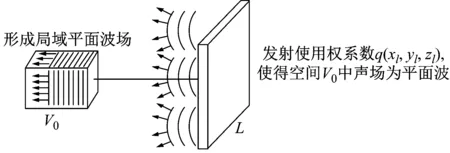
图6 空间L上的收发合置换能器形成空间V0中的平面波Fig.6 Transducers in space L forms plane wave in space V0 by weighting function q(xl,yl,zl)

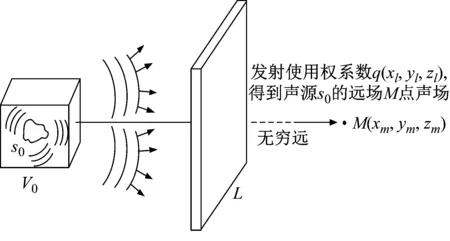
图7 空间V0中声源s0的远场辐射获取Fig.7 Far-field radiation acquisition for sound source s0 in space V0

采用这种方法一次仅能获得声源在某一方向上的指向性，不同方向上的指向性可通过两种方法获取：① 旋转声源。通过原地旋转声源s0，获得声源在不同方向上的远场取值，归一化后得到声源的指向性函数；② 调整权系数函数q(xl,yl,zl)。通过调整虚拟待测点M的方位，获得不同的权系数函数q(xl,yl,zl)，当空间V0中平面波的掠射角为(α,θ)时，所获得的是(-α,-θ)方向上的声源远场结果。第二种方法能够在声源和观测空间L位置均保持不变的情况下，获得声源在不同方位的指向性。

3 声场测量范围分析

受空间V0、L尺寸和相对位置的限制，图1所示的测试结构并不能获得声源在空间任意位置的声场，EFT能测量的空间范围有限。由前面的推论可知，当M点在空间V0中激发的声场与L在空间V0中激发的声场一致时，才能够通过观测空间L上的观测结果得到M点的声场取值。因此，从声的传播规律来分析，图1所示结构系统所能测量的空间范围与L在空间V0中能够激发的声场有关。从声场互易原理分析，EFT的测量空间也可以理解成声源V0发出的声波被L完全遮挡的空间范围。

(1) 自由场中的声场获取范围

当声源处于自由场中时，声线按直线传播，能够获取的声场范围是图8中从L右侧完全观测不到V0的区域。假设V0是发光体，L是不透光的遮挡物，那么能够获取的声场空间范围是L外侧完全黑暗的区域。

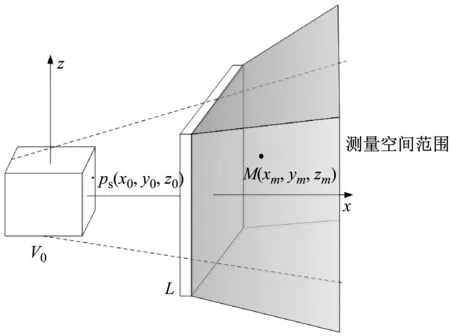
图8 声场的声场获取范围Fig.8 The sound field acquisition range of NAT

当L较小时，L外侧完全黑暗的区域是图9中的灰色空间区域，能够获取的空间区域是L～A之间的锥形区域。随着L的逐渐缩小，锥形的长度逐渐减小，直到L与A点完全重合。此时，EFT的声场获取范围仅有一个点，且该点与L重合。

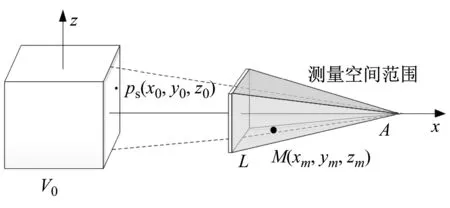
图9 当L较小时的声场获取范围Fig.9 The sound field acquisition range when L is small

当L包绕声源所在的空间V0时，如图10所示。EFT的声场获取范围是L以及L的整个外空间。

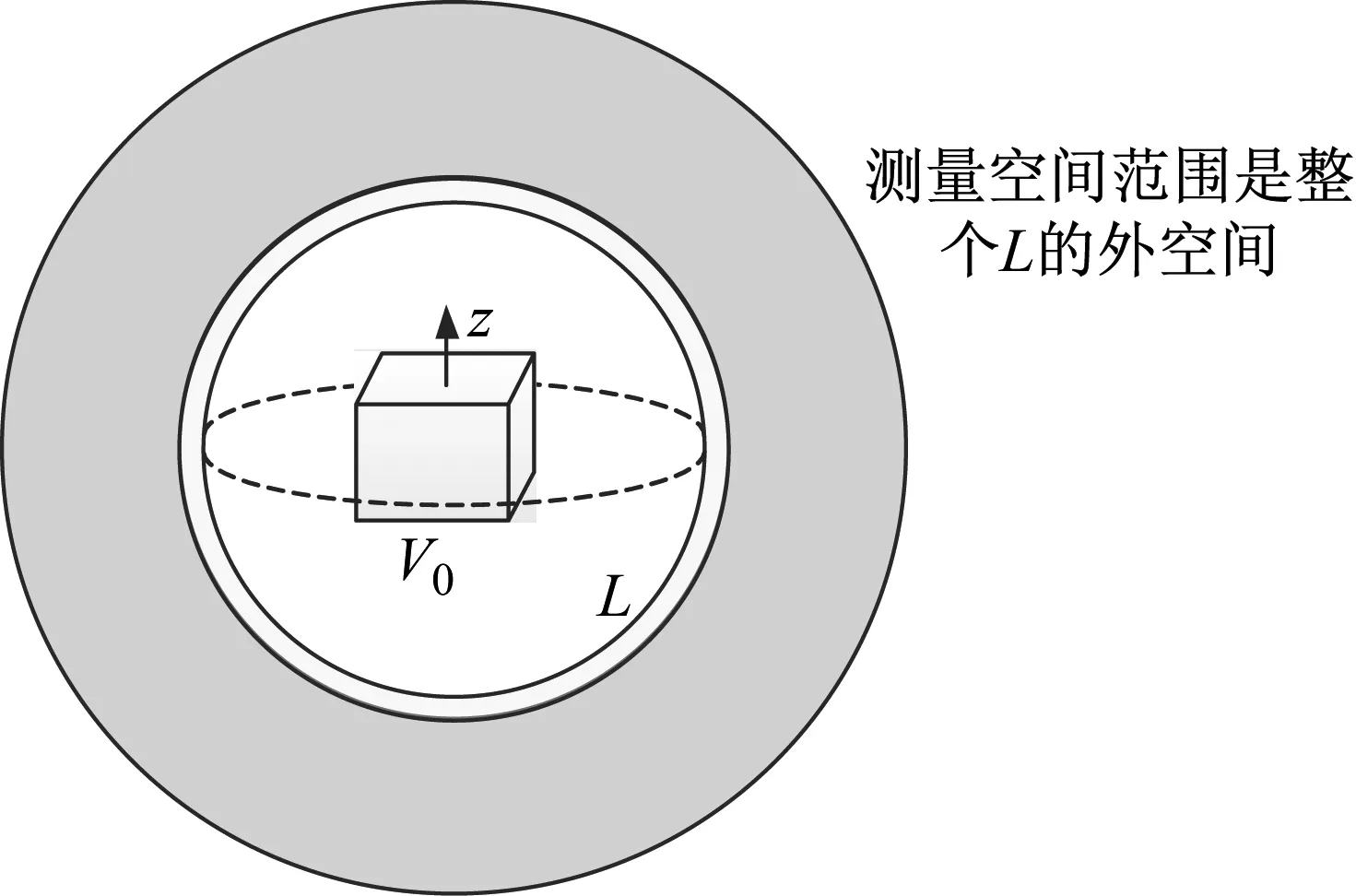
图10 L包绕声源空间V0的情况Fig.10 The measurement space range where L surrounds the sound source space V0

(2) 浅海环境中的声场获取范围

当测量系统位于浅海环境时，观测空间L会在海面和海底镜反射的影响下扩展垂直方向上的尺度，如图11所示。测试的声场获取范围是L及L右侧在y方向呈一定辐射开角的半空间。

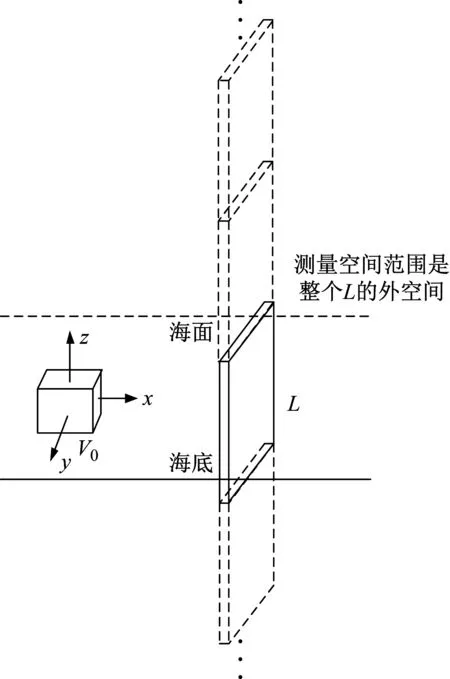
图11 浅海波导中的声场获取范围Fig.11 The measurement space range in shallow water

以上给出了不同条件下基于EFT理论的声场获取范围，在实际应用中须具体分析是否能够通过L上收发合置换能器在空间V0激发出所需的声场结构，即公式(5)中权系数函数q(xl,yl,zl)的解是否存在。这与空间V0、L的大小、位置以及测试频率有关。在空间V0小、L大、频率低的情况下，容易在空间V0激发出所需的声场结构；反之困难。

4 声场仿真验证

EFT通过观测空间的观测结果得到空间某一点/方向的声场，而非一片区域的声场，相当于在已知多个相关参数条件下，只获取一个参数。由此可以推测，EFT的声场获取精度是有保障的。下面通过声场数值仿真对该理论做进一步的验证。

观测空间中的收发合置阵元个数N=20，在H=15 m的垂直空间呈直线均匀分布。以垂直收发阵列的顶点为原点，垂直方向为z轴，建立如图12所示的坐标系。声源采用连续线阵，中心点的坐标位置(R,H/2)，其中R=7.5 m。声源长度l=1 m，工作频率f=2 kHz。

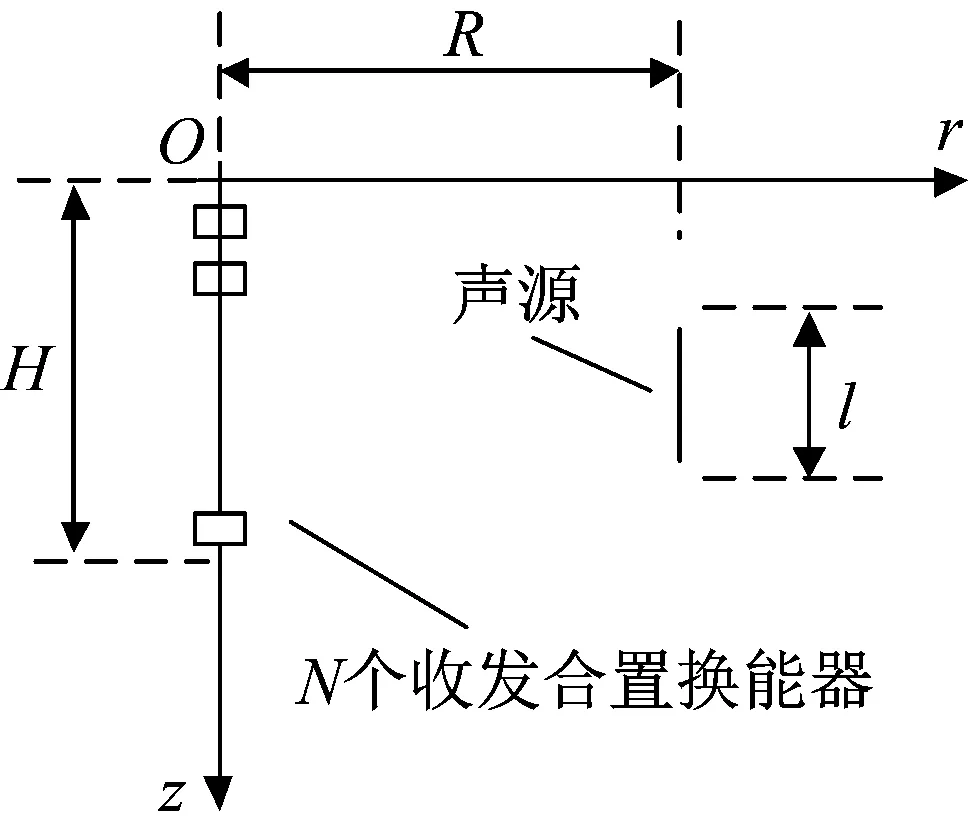
图12 自由场测试布置图Fig.12 Free-field testing layout

假设观测点M位于(-5 m,H/2)，位于该点的无指向性单位点源所发出的声场如图13所示。

以(R,H/2)为中点、边长1.5 m的立方体作为目标空间V0。调整收发合置换能器的权系数qi(i=1,2…N)，使得在V0中产生的声场与图13中该区域的声场一致。

当垂直阵未经过加权，得到结果如图14(a)所示，加权后得到的声场如图14(b)所示。水平6.75～8.25 m和垂直6.75～8.25 m包围的区域是目标区域。将加权后得到的声场与目标声场做复数差(声压场取复数)再取绝对值，然后除以图13中V0区域的平均声场幅度，得到声场的相对误差，如图14(c)所示。V0所在位置的误差最小。图14(d)所示是垂直发射阵加权后的声场相位，图中V0所在位置的相位与图13(b)中V0所在位置的相位相同。图14(c)、(d)说明垂直阵在权系数qi(i=1,2…N)的作用下，在V0区域形成的声场与点声源(-5 m,H/2)形成的声场一致。

加权系数的取值如表1所示。取值是复数，复数的模代表对信号的幅度调整，相位代表对信号相位的调整。

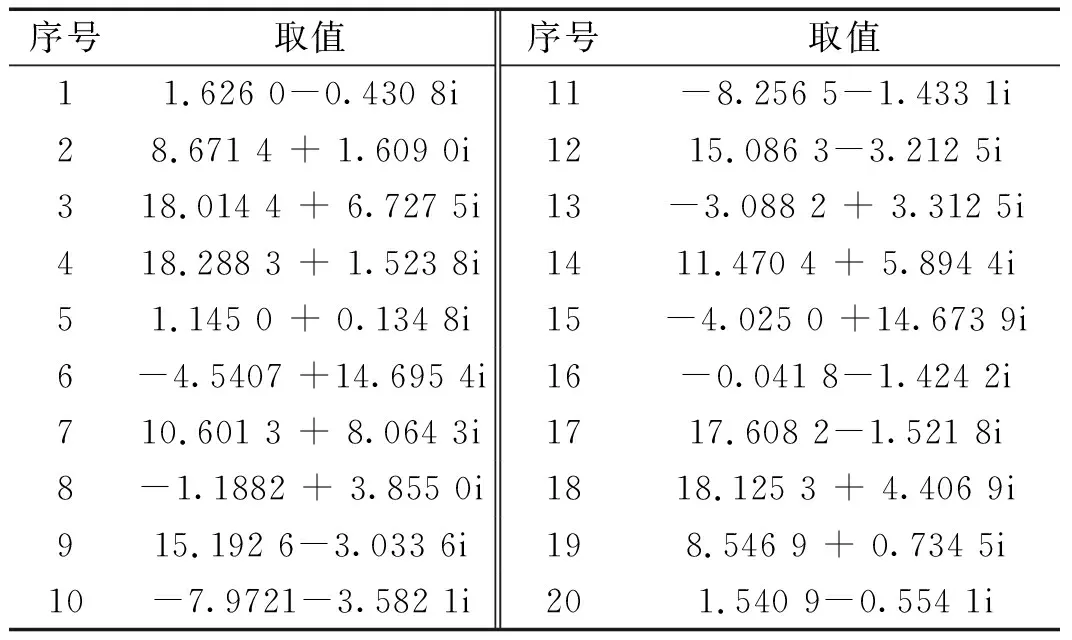
表1 加权系数Tab.1 The weighting factors

将连续线源放入目标区域，声源的辐射声场如图15所示，可以观察到辐射声场具有明显的指向性。

图15 线声源激发的声场Fig.15 The radiated sound field of a line source

旋转声源，由垂直阵接收声源的辐射声，通过表1所示的加权系数对接收到的声信号加权，获得声源在待测点M的声场。如图16(a)所示，是EFT与理论结果的对比，可以发现它们基本重合。图16(b)、(c)、(d)分别是2.5 kHz、3 kHz和4 kHz的结果对比，可以观测到EFT得到的结果与理论值一致。

将测试环境改为浅水，水深15 m，换能器和声源中心点均处于7.5 m深度，其余条件不变，如图17所示。

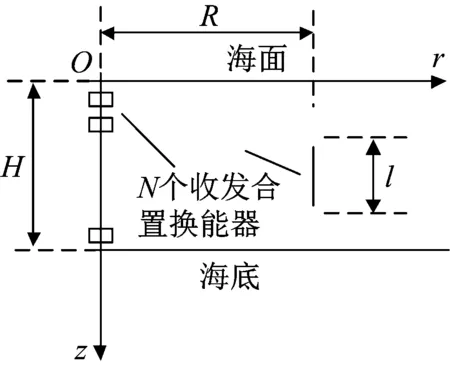
图17 浅海测试布置Fig.17 The shallow water testing layout

图18(a)是未加权的垂直阵在浅水激发的声场，可以发现声场分布起伏不定。图18(b)是加权后垂直阵在浅水激发的声场，在声场中间目标区域形成了一个声场相对平坦的区域。将图18(b)所示的声场与图13所示的声场相比较，取相对误差，得到图18(c)，颜色越亮表示误差越小，可以发现中间目标区域的误差最小。图18(c)是垂直阵加权后在浅海激发声场的相位，中间区域的声场相位与图13(b)所示中间目标区域的相位一致。说明垂直阵在目标区域V0激发的声场与自由场中无指向性单位点源M在目标区域V0激发的声场一致。此时，垂直发射阵使用的权系数就是待求参数q(xl,yl,zl)的解。

将待测声源放入目标区域，旋转声源，由垂直阵的观测值与权系数q(xl,yl,zl)测得不同频率下声源的指向性，如图19所示。可以观测到EFT得到的结果与理论结果吻合。

5 结 论

相比于NAH先获取源面的振动数据，再估算声源的辐射声场，提出了一种目标声辐射获取新理论——等效场变换理论(EFT)。该理论通过对观测空间的观测结果进行加权，获取目标空间内任意声源在待测点的声场。该理论无需声源的外形几何信息，与声源的材质和所处运动状态均无关。EFT能够应用于混响场条件，可获取指定空间内任意声源在自由场中的辐射声场或指向性。进一步给出了EFT理论中权系数的选取标准和判别依据。讨论了当需要获取声源的远场指向性时，目标空间中的声场结构为平面波。分析了自由场、浅海环境条件下，EFT方法的所能获取的声场范围。环境越复杂，EFT的测量范围反而越广阔。最后在自由场和浅水环境下对EFT法获取有限长线源的散射声场进行了数值仿真，得到的结果与自由场中理论结果吻合，验证了EFT理论的正确性。受文章篇幅限制，本文现阶段只考虑了自由场与浅海波导声场，下一步将研究EFT在其他类型条件下的应用。该理论为解决复杂环境下复杂声源的辐射计量问题提供了新思路。