三稳态电磁式涡激振动俘能装置发电性能研究

2022-07-14吴子英常宇琛李永越刘丽兰

振动与冲击 2022年13期

吴子英，常宇琛，赵伟，李永越，刘丽兰

(西安理工大学机械与精密仪器工程学院,西安 710048)

流致振动现象初期研究重心主要集中在如何抑制流致振动对高耸建筑物海洋结构物[1-2]的危害，如广东虎门大桥也受到了流致振动的危害。此外，科学界也对流致振动现象进行开发利用，提出了基于流致振动的能量捕获装置，较为典型是基于涡激振动和驰振的能量捕获装置，基于流致振动的能量捕获研究也成为了能量捕获领域的热点话题[3-4]。

较为成功的最早研究涡激振动能量捕获装置的是美国密歇根大学Bernitsas等[5]提出的涡激振动能量发电装置VIVACE，该装置利用海洋洋流流经圆柱体时，引发圆柱体产生涡激振动从而带动电磁感应式转子发动机发电来捕获流体动能，成功开创了人类在海洋洋流能量利用中的里程碑。涡激振动能量捕获装置多样，多采用压电悬臂梁连接圆柱形钝体型结构，如宋汝君等[6]提出的复摆式涡激振动俘能器，分别从理论和实验角度研究了水流流速与俘能功率之间的关系。罗竹梅等[7]提出了串列、并列和错列布置的耦合连接型五圆柱柱体结构涡激振动俘能器，获得了柱群俘能结构集中俘获低速海流能的初步理论。在结构参数影响研究方面，白旭等[8]分析了低阻尼条件下不同质量比对涡激振动能量捕获效率的影响。曹东兴等[9]从理论和实验角度较为详细的研究了流速、圆柱体直径、磁间距、磁极和外接电阻等系统参数对俘能器振动特性及输出电压的影响。

目前的涡激振动俘能装置多可以简化为线性振动系统，共振带宽过窄；相较于线性振动，非线性振动因具有较宽的工作带宽，所以基于非线性振动的俘能装置受到了国内外学者的广泛关注。如Ma等[10]针对如何提高非线性频宽做了大量研究；首次使用了两段线性弹簧建立非线性系统使得俘能装置在过渡区域也可使用，提出了自适应非线性刚度理念；实验证明，此装置可在水速0.275 m/s以上充分俘能，俘能效率较传统的线性系统有较大提升。Qin等[11]建立了涡激振动和驰振复合振动装置(BPEH)，引入双稳态系统进一步提高俘能效率；该装置在全流速范围内，涡激振动和驰振相互发挥耦合作用，可以适应复杂激励的流速场。谭洪波等[12]提出了一种多稳态驰振能量捕获器，对其动力学响应和发电性能进行了数值仿真研究；三、四稳态系统有较浅的势阱，在较小的外界激励能量下，系统易产生大幅运动模式。

本文将弹簧提供的三稳态特征与电磁式涡激振动能量发电装置相结合，提出了一种三稳态电磁式涡激振动俘能装置，通过引入单向离合器校正发电机输入轴的转动方向，使用三相交流电磁发电机实现能量转换，通过数值仿真分析非线性系统参数对发电性能的影响规律，分析能量俘获装置结构参数、单向离合器以及飞轮大小对涡激振动俘获装置发电性能的影响规律。

1 三稳态涡激振动俘能装置和力学模型

1.1 三稳态涡激振动俘能装置模型

涡激振动是由于流体黏性作用使得其在绕流圆柱体后侧产生了交替脱落的漩涡，从而引起了柱体横向的往复运动，如图1所示。

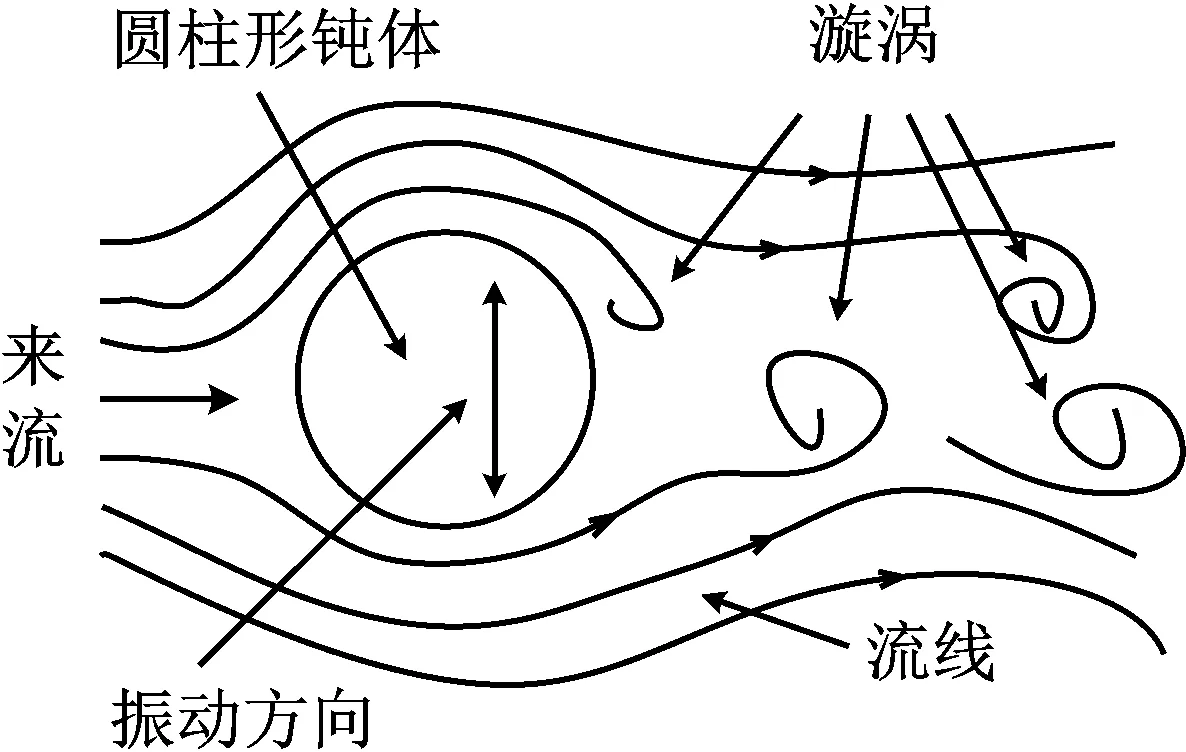
图1 涡激振动原理示意图Fig.1 Schematic of vortex induced vibration

本文通过引入非线性回复力和单向离合器，提出的一种可进行钝体上下两个振动方向动能捕获的新型三稳态电磁式涡激振动俘能装置，如图2所示。图2中，在中心轴6上左侧安装有左齿轮4、正向单向离合器14，中心轴6右侧安装有右齿轮7、反向单向离合器13，左/右齿轮分别通过正向/反向单向离合器与中心轴6相连，中心轴6借助联轴器12与发电机11和飞轮10相连，钝体1固定在钝体支架15末端，钝体支架15在直线导轨3中上下滑动，左右齿轮同时与钝体支架相连，弹簧2安装在钝体支架15与机架5间。圆形截面钝体1在水流的冲击下产生上下运动，当钝体1向上运动时，钝体支架15带动左齿条17和右齿条16同时向上运动，由于正向/反向单向离合器工作方式不同，正向单向离合器14工作，此时，反向单向离合器13不工作，从而左齿条17带动与其啮合的左齿轮4转动，而右齿轮8不发生转动，左齿条17、左齿轮4、正向单向离合器14通过中心轴6将钝体1的向上直线运动转换为驱动转子发电机11发电的旋转运动。当钝体1向下运动时，右齿条16驱动右齿轮7转动，反向单向离合器13工作，正向单向离合器14不工作，此时左齿轮4空转，右齿轮7将钝体1向下的直线运动转换为驱动转子发电机11发电的旋转运动。在水流的冲击下，钝体1上下运动，发电机11始终朝着一个方向转动。

1-圆形截面钝体；2-弹簧；3-直线导轨；4-左齿条；5-左齿轮；6-机架；7-中心轴；8-右齿轮；9-右齿条；10-固定板；11-飞轮；12-转子发电机；13-联轴器；14-反向单向离合器；15-右齿条；16-正向单向离合器；17-钝体支架图2 三稳态涡激振动俘能装置模型Fig.2 3D model of tristable vortex induced vibration energy harvester

1.2 非线性回复力

本文的非线性回复力建模借助Yang等[13]的思想，如图3所示。

图3中，中心惯性质量M由一个水平支撑弹簧和一对斜弹簧支撑，具有Ks(N/m)刚度的弹簧起到了恢复机构的作用；当外部激励作用于M(钝体)时，钝体以y(t)方向振动。虽然每个弹性构件都提供线性恢复力，但由于几何构型的关系，产生的力具有很强的非线性。是非线性系统的几何参数，其a,b,c,l为弹簧的正常状态长度。采用质量M来决定整个系统的质量，因其质量远大于弹性构件的质量，故弹簧的动质量总和可以忽略不计。

对于给定的位移，非线性系统的弹性势能Us表达式如下：

(1)

(2)

选取参数a=0.07 m、b=0.02 m、c=0.015 m、Ks=200 N/m、l=0.05 m，由式(1)可得出势能函数如图4，可看出具有明显的三稳态特征。

图4 三稳态系统势能图Fig.4 Tristable potential energy function

1.3 尾流振子方程

Hartlen等[14]最早提出了流固耦合的尾流振子模型，把流场近尾迹动力学用振子来模化；采用Van der Pol方程来描述近尾迹流场的振荡特性，计算得到了正确的升力变化规律。Facchinetti等[15]在流固耦合模型中分别采用结构的位移、速度和加速度来耦合并表示流体振子的运动过程，通过对比计算，认为采用加速度描述振子的受力最为理想。本文亦采用加速度项来描述本文发电装置的流固耦合现象，Van der Pol尾流振子的方程为

(3)

式中：q为无量纲参数，意为尾流振子；ε为非线性项中的小参数；A为结构对流体的耦合动力参数。尾流振子无量纲参数q定义为

(4)

式中:CL是流体对结构的瞬时升力系数；CL0是对应的静态圆柱体横向升力幅值；Ωf表示漩涡脱落频率

(5)

式中：U为流体的流速；D为刚性圆柱体的外径；St为斯特劳哈尔数。

1.4 三稳态涡激振动俘能装置力学模型和动力学方程

该涡激振动俘能装置由两部分构成：水流和非线性弹簧支承的钝体相互耦合作用而构成的尾流振子系统；单向离合器、齿轮与转子式发电机构成的转子发电系统。对图1所示结构模型进行力学简化，将圆形钝体和齿条简化为如图5所示的集总质量。

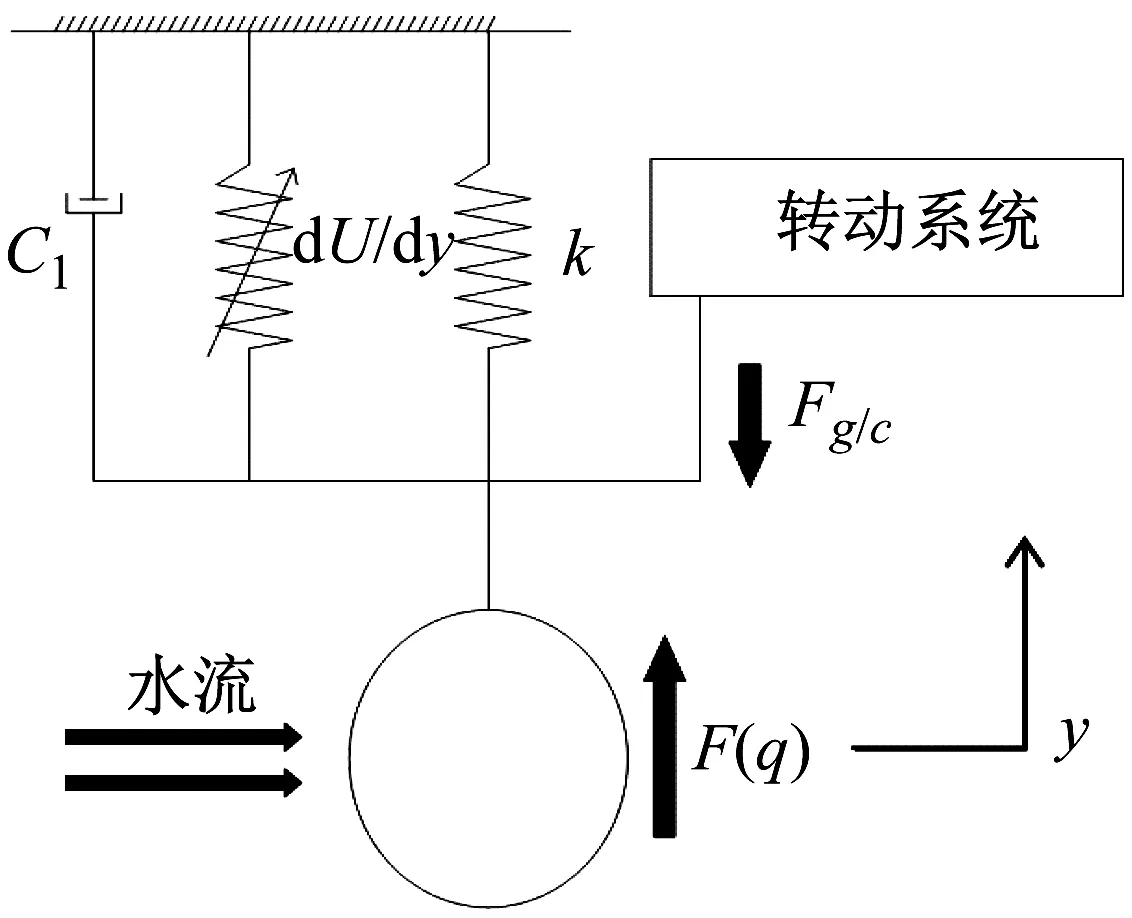
图5 钝体系统力学模型Fig.5 Mechanical model of bluff vibration system

根据牛顿第二定律和尾流振子方程，可以得到直径为D的单自由度非线性弹簧支承的刚性钝体在自由流速度为U的平稳匀速流动中的动力学方程为

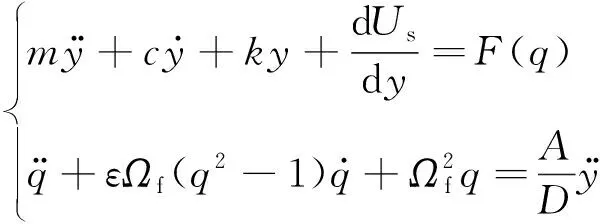
(6)

式中：m为刚性圆柱体质量和流体附加质量，即m=ms+ma；ms为圆柱体质量；ma为流体附加质量，即ma=1/4CmρπD2L；Cm为附加质量系数；ρ为流体密度；c为结构阻尼cn和流体阻尼cf之和，c=cn+cf；cf为流体阻尼，cf=γΩfρD2；F(q)为水流激励力，F(q)=1/4ρU2DCL0Lq；L为钝体长度。

1.5 转子系统力学模型和动力学方程

将齿轮、单向离合器、转子发电机和飞轮部分简化为如图6所示的转子系统模型。

图6 转子系统力学模型Fig.6 Schematic of nonlinear restoring force

在转子系统工作过程中，由于钝体上下振动的速度变化，导致左/右齿轮的转速也发生变化，发电机也处于运转状态，此时会出现两种工作状态：① 左/右齿轮转速大于发电机的转速，钝体的动能能量通过齿轮、单向离合器到发电机，转化为电能，此时钝体和发电机处于结合状态；② 左/右齿轮转速小于发电机的转速，由于单向离合器只有在输入转速大于输出转速时才起作用[16]，所以钝体的动能能量无法通过齿轮、单向离合器到发电机，此时钝体和发电机处于脱离状态。因此需要将上述两种状态分别进行建模研究。

在结合状态下，水流力F(q)通过钝体和单向齿轮结构传递到发电机，发电机产生阻力

(7)

综上，得到结合状态下三稳态涡激振动俘能装置流固电耦合的动力学方程为

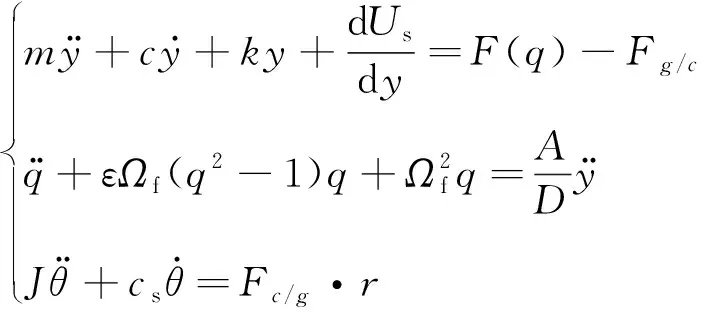
(8)

式中：Fg/c是发电系统对钝体系统的阻力，与此同时也是发电系统的动力，所以Fg/c和Fc/g大小相同，方向相反；J是齿轮、中心轴、发电机和飞轮的总转动惯量；Cs是发电系统的阻尼系数；r为齿轮半径。

根据法拉第感应定律得到角位移引起电动势的电压UVIV

(9)

进一步可得到俘能装置的发电功率表达式P

(10)

式中：ke为电势系数；RL为发电机外电阻；Ra为发电机内电阻。

(11)

式(11)的解可写为

θ=θ0e-(ceq/J)t

(12)

式中:θ0为发电机的最大转速;t为衰减时间。因此，脱离周期的阻尼力和输出电压为

(13)

综上，得到脱离状态下，三稳态涡激振动俘能装置流固电耦合的动力学方程为

(14)

2 数值仿真

相对于双稳态势能函数，三稳态势能函数具有3个稳定平衡点和2个不稳定平衡点，势阱深度较双稳态浅，在较弱的外界激励下三稳态系统通常更易产生大幅运动模式。单向离合器结构具有速度相反运动校正功能，从而使本文的俘能装置具有更高的发电效率。主要从以下两个方面进行数值仿真研究：① 将三稳态涡激振动俘能装置与双稳态涡激振动俘能装置发电性能对比，探究三稳态能量捕获器的特点；② 研究俘能装置结构参数对发电功率的影响规律，探寻俘能装置较佳结构参数配置；探讨有无单向离合器与飞轮大小对发电性能的影响。仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

2.1 双稳态与三稳态俘能装置发电功率和动力学响应比较

2.1.1 势能函数比较

三稳态和双稳态的势能函数如图7所示。

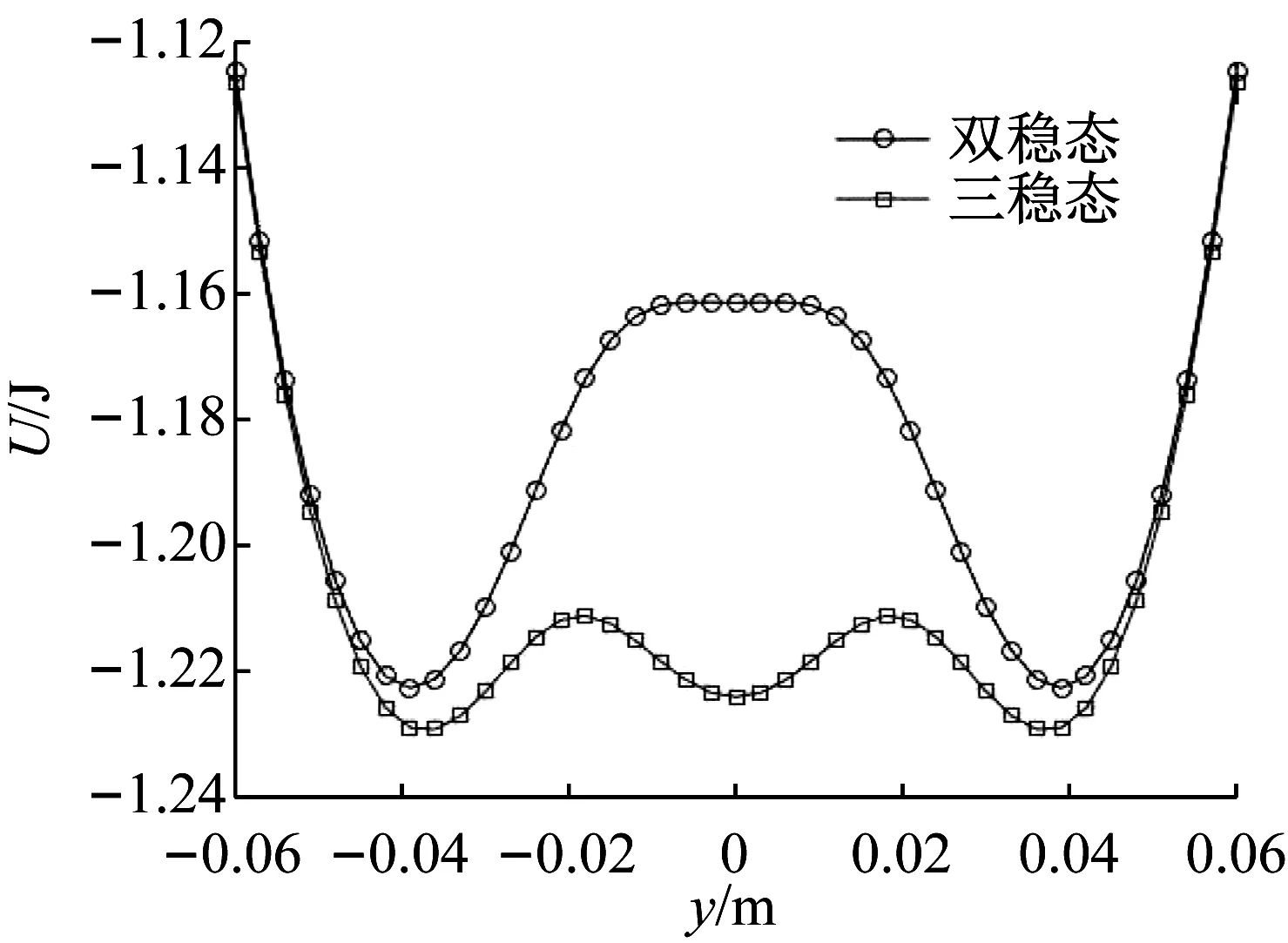
图7 两种稳态系统势能函数对比Fig.7 Bistable and tristable potential energy function

由图7可知：双稳态俘能器具有两个对称势阱和一个势垒，而三稳态俘能器具有三个势阱和两个势垒。从图中得出双稳态俘能器的势垒高度-0.062 J，而三稳态俘能器的势垒高度仅为-0.033 J，差值为0.029 J。即三稳态系统较双稳态系统势垒显著降低，在相同的外界激励下，三稳态俘能器可以更容易地越过势垒，实现大幅度运动。

2.1.2 振幅比和发电功率

在流致振动研究中，通常采用振幅比(A*)来描述钝体的位移幅度，振幅比(A*)被描述为实际位移与钝体的半径的比值，即：

A*=y/D

(15)

两种系统的振幅比和发电功率如图8所示。

由图8可知:① 在引入三稳态系统之后，在振幅比的峰值数值高于双稳态系统；且无论是双稳态或是三稳态系统，都会随着流速的继续增加而减小；这是因为钝体采用圆柱体，发生“涡激振动”现象；涡激振动显著的特点是较低流速下产生涡激共振使发电装置的振动幅值最大，且存在“自限性”现象;② 随着流速的增加，两种俘能系统功率的变化曲线同样遵循涡激振动的“自限性”现象：在流速为0.32 m/s时，取到最大值，随后流速再增加，功率减小；三稳态系统不仅在峰值高于双稳态，且降低的速率也明显慢于双稳态。说明从发电性能来看，三稳态系统远远优于双稳态系统。通过与文献[9]的研究结果相比，本文的仿真研究结果与文献[9]的研究结果有相似性，也证明了本文的结果有一定的正确性。

综上，可得出部分结论：① 引入双稳态和三稳态后，阻流体的振动均出现了在一定流速范围内，随着流速的增大而增大的趋势，且之后出现了“自限性”现象；② 相对于双稳态，引入三稳态后的钝体随着流速的增大，其振幅比增大的幅度较大；且发电功率都有明显的提升，说明三稳态系统较双稳态系统来说有更优良的发电性能。

2.1.3 动力学响应

为了进一步分析振幅比情况，我们选取图8曲线中三个速度点U=0.22 m/s，U=0.32 m/s和U=0.42 m/s，得到钝体的相图与振幅比图，如图9～图11所示。

从图9、图10和图11可以看出，在三个流速的情况下，双稳态和三稳态俘能装置钝体的增大速度大小基本一致，但与双稳态俘能装置，三稳态俘能装置的钝体振幅比更大。

根据式(5)可以计算出三种流速0.22 m/s、0.32 m/s和0.42 m/s的漩涡脱落频率分别为0.44、0.63和0.83 Hz，对式(6)进行扫频数值仿真，得到三稳态涡激振动俘能系统中钝体的振动幅值响应曲线，如图12所示。

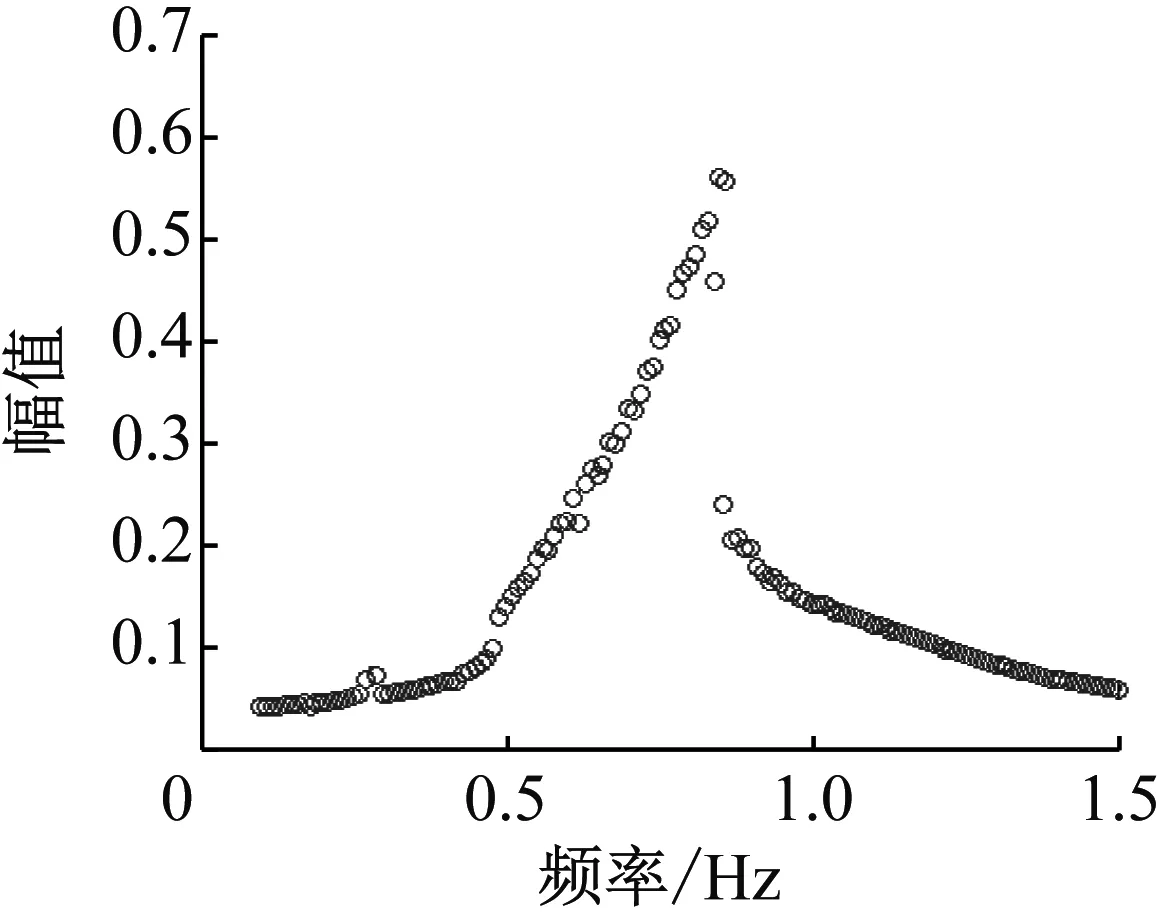
图12 非线性幅频响应曲线Fig.12 Nonlinear Relationship curve of vibration amplitude of TVIVEH vs. frequency

从图12可以看出，文中三稳态涡激振动俘能装置具有非线性振动特征，共振频带较宽，漩涡脱落频率也位于非线性共振频带中，随着漩涡频率的增大，俘能系统非线性振动的幅值也随之增大，从0.8左右振幅有所下降，侧面验证了理论建模的正确性。

2.2 质量比对系统的影响

质量比m*的定义为钝体的结构质量与其排开水的流体质量之比，数学表达如式(16)所示

(16)

分别取质量比m*=1.02,1.27，1.66,1.91；其他参数分别取值为D=100 mm，RL=10 Ω；四个质量比下俘能装置发电功率的仿真结果如图13所示。

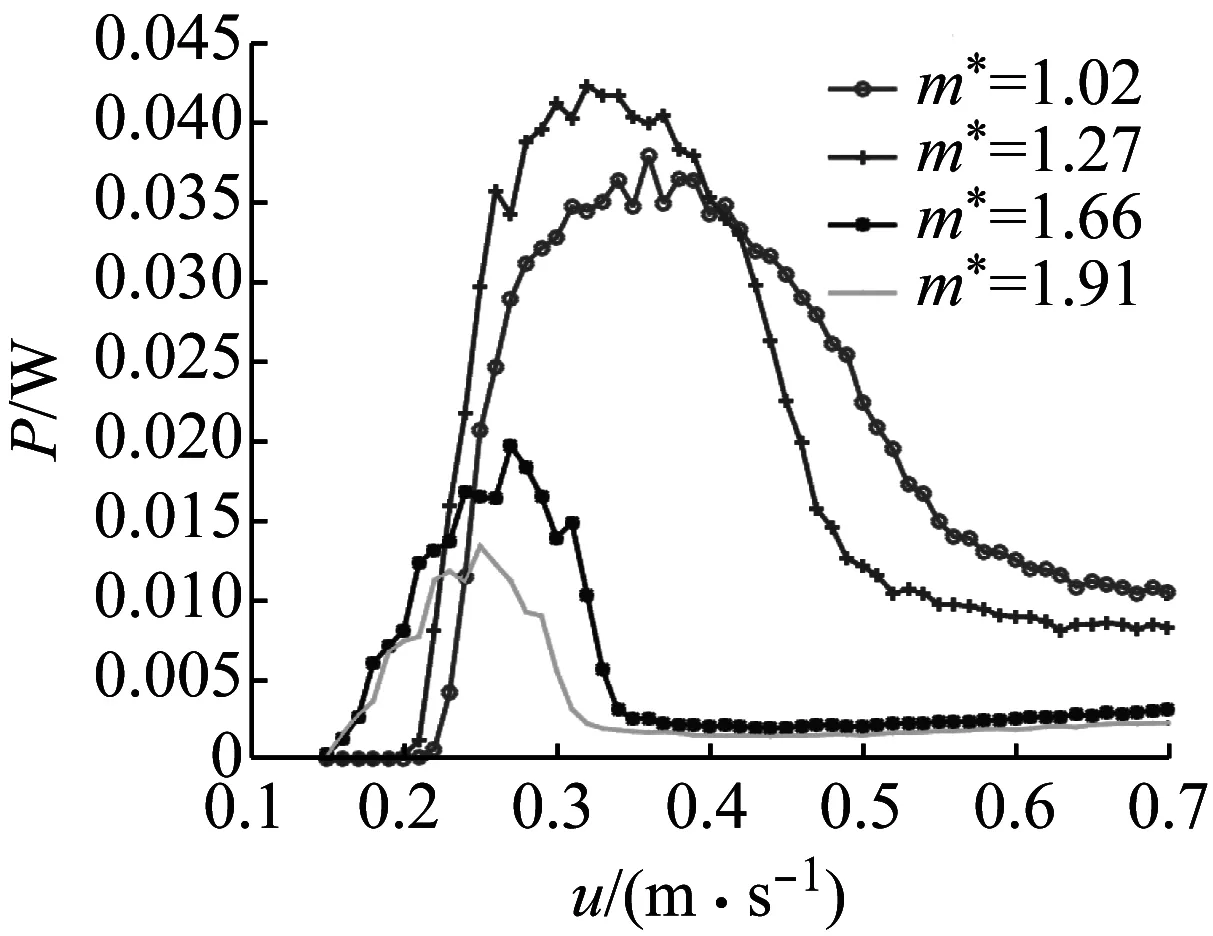
图13 不同质量比下功率随流速变化曲线Fig.13 Relationship curve of power of TVIVEH vs. water velocity under different mass ratio

从图13可以看出，三稳态涡激振动能量俘能器系统在不同质量比下平均功率趋势均为快速增长然后下降趋势；且当质量比大于1.27时，随着质量比的增加，俘能装置的发电功率在不断减小。说明质量比为1.27时，俘能装置发电性能较佳。

2.3 钝体直径对系统的影响

钝体直径主要影响涡激振动的涡脱频率和尾流钝体q，因此钝体直径的选取要在适宜的范围内，取钝体直径90 mm，100 mm，110 mm和120 mm，根据图13，其他关键参数分别取值为m*=1.27，RL=10 Ω；四个钝体直径下俘能装置发电功率的仿真结果如图14所示。

图14 不同钝体直径下功率随流速变化曲线Fig.14 Relationship curve of power of TVIVEH vs. water velocity under different diameter of bluff

从图14可以看出，三稳态涡激振动能量俘能器系统在不同钝体直径下其平均功率趋势均为快速增长然后下降趋势；且当直径大于100 mm时，随着直径的增加，发电功率在不断减小。

为了准确分析钝体直径对装置发电性能的影响规律；取U=0.32 m/s时，分析不同的钝体直径对于发电性能的影响，如图15所示。

图15 不同钝体直径装置发电功率曲线Fig.15 Relationship curve of power vs. diameter of bluff

由图14和图15可知，在质量比m*=1.27直径为100 mm时，该系统的钝体直径可获得最大发电量。

2.4 负载电阻对系统的影响

三稳态涡激振动电磁式发电装置的发电系统的电阻主要分为发电机内阻(Ra)和负载电阻(RL)；发电机内阻是随发电机不同而固定的数值，而本节则是在探究不同的负载电阻对装置的发电性能特性有何影响；分别取RL=5 Ω，10 Ω，15 Ω，20 Ω，其他关键参数分别取值为m*=1.27，D=100 mm；四个负载电阻下俘能系统的发电功率如图16所示。

图16 不同负载电阻下功率随流速变化曲线Fig.16 Relationship curve of power of TVIVEH vs. water velocity under different load resistance

由图16可知，三稳态涡激振动能量俘能器系统在不同负载电阻下平均功率趋势均为快速增长然后下降趋势；且当负载电阻大于10 Ω时，随着负载电阻的增加，发电功率在不断减小。

为了准确分析负载电阻对装置发电性能的影响规律；取U=0.32 m/s时，保持质量比参数1.27和直径参数100 mm不变，分析不同的负载电阻对于发电性能的影响，如图17所示。

图17 不同负载电阻装置发电功率曲线Fig.17 Relationship curve of power vs. load resistance

由图16和图17可知，负载电阻为10 Ω时，俘能装置输出功率最大，该负载电阻值为该系统的最优参数。

2.5 单向离合器和飞轮大小的影响

飞轮是利用自身转动惯量来吞吐能量，从而减少发电机转速的速度波动，使输出功率更平稳。分析有/无单向离合器(记为MMR/No-MMR)时，俘能装置发电功率变化情况，同时也给出了两种不同转动惯量(即0.000 7 kg·m2和0.000 2 kg·m2)飞轮下的发电功率情况，如图18所示。

图18 有/无飞轮和有大/小飞轮下功率曲线Fig.18 Relationship curve of power of TVIVEH vs. time with/without large/small moment of inertia

由图18可知：

(1) 有单向离合器：转动惯量较大的飞轮可以使得运动较为平缓；在脱离状态下，大转动惯量转子系统的速度下降的速度要低于小转动惯量转子系统的速度下降的速度，说明大飞轮的转子系统可以俘获更多的可利用能量；在流体的输入能量固定的情况下，该结构可以有效的提高装置的俘能效率。与文献[16]的研究结果对比，本文的仿真结果与文献[16]有较大相似之处，也佐证了本文研究的正确性;

(2) 无单向齿轮结构：俘能装置仅仅俘获了上下运动中的一个方向的振动能量，无论是大小转动惯量，都基本不会影响到装置的俘能功率和俘能效率；飞轮的转动质量的改变对于整个系统来说，影响很小，可以忽略不计。