齿轮-轴承传动系统擦边碰撞的动力学特性分析

2022-07-14高建设崔秉奇丁顺良杨林杰

振动与冲击 2022年13期

高建设，崔秉奇，丁顺良，杨林杰

(1.郑州大学机械与动力工程学院，郑州 450000； 2.郑州机械研究所，郑州 450000)

齿轮传动由于具有传动准确、可靠性高等优点，渐渐成为广泛使用的传动装置之一。随着对齿轮性能要求的提高，如何减少齿轮副冲击振动和噪声是当前亟待解决的关键问题[1]。为便于润滑和防止齿轮热膨胀卡死，齿轮间需具有适当的齿侧间隙，这会导致齿轮副齿面存在冲击、碰撞等现象，对齿轮的性能、寿命等诸多方面产生一定的影响。例如，随着齿面的磨损或工况的细微变化，冲击可能会导致原本正常的周期运动突变为异常的振动，影响齿轮的使用寿命甚至安全性。因此，对齿轮系统的冲击特性进行深入的研究，不仅有利于推动非光滑动力学的发展，而且有利于识别齿轮系统可能出现的不利工况，更重要的是通过分析齿轮系统的运动状态来获得理想的工作条件，避免冲击碰撞以降低噪声、增加齿轮寿命，提高齿轮系统的工作性能。

目前，齿轮系统动力学特性已经被广泛地研究。向玲等[2]运用周期扩大法的思想，研究了支承阻尼对多自由度齿轮系统的影响。田亚平等[3]运用PNF法和延续算法对单级齿轮系统的周期运动进行了分析。Shi等[4]建立含接触比的时变齿隙模型，研究了转速、扭矩载荷和齿面温度对时变齿隙的影响。林何等[5]基于OGY混沌控制理论对齿轮-轴承系统的混沌运动进行了多周期控制。陈思雨等[6]研究了在考虑时变刚度和摩擦时，轮齿间隙及载荷参数对齿轮系统冲击动力学响应的影响。唐进元等[7]基于图胞映射法讨论了时变啮合刚度和摩擦对系统全局特性的影响。He等[8]建立了考虑滑动摩擦和真实时变刚度的多自由度齿轮模型。上述研究为齿轮系统动力学的研究提供了重要思路。但关于齿轮副间擦边碰撞的研究较少，其动力学机理仍然不是十分清楚。尹桩等[9]研究了重合度为1的单级齿轮啮合过程中齿面冲击对系统运动状态的影响。

对齿轮系统动力学的研究主要采用频闪映射的方法，但这种方法不能展现出齿轮副啮入、啮出时的动力学特性。为此，本文以含间隙齿轮-轴承系统为研究对象，定义齿面碰撞面Poincaré映射以及齿背碰撞面Poincaré映射，结合分岔图、啮合力变化图、相图、以及最大Lyapunov指数图等揭示齿轮副啮入、啮出冲击下系统运动状态的变化，分析擦边碰撞对系统动力学特性的影响。

1 齿轮-轴承系统动力学模型

齿轮-轴承系统由轴承支撑和齿轮副组成[10]，假设主、从动齿轮均为标准的渐开线直齿圆柱齿轮，不考虑运动时齿轮副、支撑轴承的摩擦力，且忽略轴的弯曲和变形。

基于上述假设，齿轮-轴承系统简化模型如图1所示。

图1 齿轮-轴承传动系统简化模型Fig.1 Simplified model of gear-bearing transmission system

其动力学方程如下[11-13]

(1)

主、从动齿轮的转动惯量、质量、基圆半径、扭转角位移、轴承的支撑力、外力矩、啮合阻尼、支撑刚度分别用Ii，mi，Ri，θi，Fi，Ti，ci，ki(i=1,2)表示，时变啮合刚度、静态传递误差、啮合阻尼、齿轮等效质量、沿啮合线载荷、波动载荷用kh(t)，e(t)，ch,mc,Fm,FaT(t)表示，fi(yi)和fh(p)分别表示轴承径向间隙和齿侧间隙的位移函数，表达式如下

(2)

(3)

其中

x=R1θ1(t)-R2θ2(t)

p=x+y1-y2-e(t)

Fm=T1/R1=T2/R2

FaT(t)=m1T1(t)/2I1

式中:kh(t)[14]以谐波级数形式展开;khm为平均啮合刚度;khar(r=1,2,…)为各谐波分量系数;φhr为对应相位角;ω为齿轮啮合频率。

(4)

式中：x1、x3、x5表示轴承径向和齿轮啮合综合误差无量纲位移；x2、x4、x6分别表示无量纲位移相应的无量纲速度；ki3、ζi3(i=1,2,3)表示时变啮合刚度和齿面啮合阻尼系数；kii、ζii(i=1,2)表示轴承支承刚度和阻尼系数；Fm、Fah1表示负载系数和内部激励系数。

无量纲化后齿轮间隙函数和轴承径向间隙函数为

(5)

(6)

式中：D为无量纲齿侧间隙;bi为无量纲轴承径向侧隙。

用最小啮合综合误差xmin与齿侧间隙D来判断齿轮系统中存在的无冲击、单边冲击、双边冲击等冲击状态。

用F表示齿轮啮合时齿轮副之间产生的无量纲啮合力

F=-2ζ33x6-k33(t)fh(x5)

(7)

当齿轮啮合综合误差x5=D时，则齿轮副之间发生齿面擦边碰撞;若x5=-D，则发生齿背擦边碰撞。

定义符号“P-Q-R”为系统的运动状态，其中P表示系统的周期数,Q表示一个啮合周期内齿面碰撞数，R表示一个啮合周期内齿背碰撞数。即P-0-0表示无冲击，P-Q-0表示单边冲击，P-Q-R表示双边冲击。

2 Poincaré截面分析

根据系统相轨迹和碰撞面(x5=±D)相交的情况，可以分为以下几种类型[15-17]：

(1) 相轨迹和碰撞面Σ始终保持无交集的状态，即相轨迹只在区域Σ+内运动。

(2) 相轨迹从区域Σ+穿越碰撞面Σ到区域Σ-，运动一定时间后再次穿越碰撞面Σ回到区域Σ+，并且可能会发生多次类似运动。

(3) 相轨迹和碰撞面Σ相切，即相轨迹和碰撞面Σ仅相交于一点X3，整个过程中，相轨迹仅在区域Σ+内运动。

一般分析系统非线性特性使用频闪映射的方法[18-19]，但是，这种方法会掩盖碰撞面(图2碰撞点Xi(i=1,2,3))处的特性。因此，在相轨迹每次到达碰撞面时采样，若存在采样点，则说明相轨迹经过碰撞面。据此探究擦边碰撞对系统动力学特性的影响。

图2 相轨迹和碰撞面Σ相交示意图Fig.2 Schematic diagram of the intersection of phase trajectory and impact surface Σ

根据以上碰撞分析，针对模型定义三种Poincaré截面：

(1) 时间Poincaré截面

时间Poincaré截面也称频闪采样，即每隔一个激励周期2π/Ω对相轨迹进行采样。Poincaré截面可记为

σ1={(x1,x2,x3,x4,x5,x6,θ)∈6×S1,

θ=Ωt=0mod(2π)}

(2) 齿面碰撞面Poincaré截面

选择主、从动齿轮啮合综合误差x5=D作为Poincaré截面，取啮合后的瞬间建立Poincaré映射。每当相轨迹到达齿面碰撞面时进行采样，并计算此时的无量纲啮合力F，揭示此时齿轮系统所处的冲击状态。Poincaré截面可记为

σ2={(x1,x2,x3,x4,x5,x6,F,θ)∈7×S1,x5=D}

(3) 齿背碰撞面Poincaré截面

选择主、从动齿轮啮合综合误差x5=-D作为Poincaré截面，采样方法和齿面碰撞面Poincaré截面类似，Poincaré截面可记为

σ3={(x1,x2,x3,x4,x5,x6,F,θ)∈7×S1,x5=-D}

3 非线性动力学擦边特性分析

3.1 无量纲激励频率Ω对擦边特性的影响

首先研究激励频率变化下的擦边碰撞特性。忽略轴承径向间隙的非线性力-位移关系，取基准参数为：Fm=0.2,Fah1=0.05，ε=0.2，D=1.0，ξ11=ξ22=0.01，ξ13=ξ23=0.012 5，ξ33=0.05，F1=F2=0.1，k11=k22=1.25，无量纲激励频率Ω∈[0.7,1.6]。运用Runge-Kutta法对方程组(4)进行求解并计算碰撞面啮合力，结合最大Lyapunov指数图[20]分析擦边碰撞对系统的影响。

对Poincaré截面进行分析，图3为σ1截面的分岔图。图4为σ2和σ3截面啮合力F的周期变化图。其中，虚线(F=0)以下区域表示σ2截面上采样点计算的啮合力，虚线以上区域表示σ3截面上采样点计算的啮合力。图中虚线以上区域不存在点，说明相轨迹未到达齿背碰撞面。当Ω∈[0.811 75,1.301 00]时，系统处于无冲击状态，当Ω∈[0.700 00,0.811 75]∪[1.301 00,1.600 00]时，系统处于单边冲击状态。图5为最大Lyapunov指数图(the largest Lyapunov exponents, TLE)。

图3 齿轮啮合综合误差x随Ω变化分岔图Fig.3 The bifurcation diagram of gear comprehensive error of meshing x changing with Ω

图4 无量纲啮合力F的周期变化图Fig.4 The periodic variation diagram of dimensionless meshing force F

图5 最大Lyapunov指数图Fig.5 The largest Lyapunov exponent

当Ω>1.530 00时，系统为周期1运动，无量纲齿面啮合力F也为1周期，这说明主、从动齿轮每次齿面啮合时，啮入点的速度均相同，运动规律，TLE值小于零且保持稳定，此时系统处于单边冲击状态。当Ω=1.530 00时，由“1-1-0”(根据上文定义，第一个“1”代表系统周期为1，第二个“1”代表齿面碰撞为1周期，第三个“0”代表无齿背碰撞情况)向“2-1-0”转迁时发生倍周期分岔，突变点处TLE值近似为0。

当Ω=1.506 75时，无量纲齿面啮合力F趋近于0，系统发生擦边碰撞(x=D，齿面碰撞面)并发生分岔。无量纲齿面啮合力F由2周期突变为3周期，突变点TLE近似为0，系统由“2-2-0”向“4-3-0”转迁。擦边碰撞点前后的相图如图6(a)、图6(b)和图6(c)所示。当Ω=1.508 00时，相轨迹穿越σ2截面4次，发生2次脱啮。随着Ω的减小，系统发生擦边碰撞(图6(b))，系统相图的拓扑结构发生突变。可见图6(c)，相轨迹穿越σ2截面6次，发生3次脱啮。

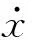
当Ω=0.811 75时，系统再次发生擦边碰撞(x=D，齿面碰撞面)，由“1-0-0”向“1-1-0”转迁，无量纲齿面啮合力F突变为1周期，但擦边碰撞未对系统周期造成影响，TLE值保持稳定。擦边碰撞前后系统相图如图7(a)、图7(b)和图7(c)所示。当Ω=0.812 50时，如图7(a)所示，系统处于无冲击状态，相轨迹全部位于x=1的右侧。随着Ω的减小，系统发生擦边碰撞(图7(b))，当Ω=0.811 00时(图7(c))，系统由无冲击状态转变为单边冲击状态，但其相轨迹和图7(a)、图7(b)相轨迹相同，其拓扑结构未发生改变，可看作是相轨迹向左平移而系统周期保持不变。

当Ω=0.804 40时，向“2-2-0”迁移时发生倍周期分岔，分叉点TLE值向0发生突变。当Ω=0.797 00时，系统再次发生擦边碰撞(x=D，齿面碰撞面)，转迁至“2-3-0”运动。此次擦边碰撞依然未对系统周期造成影响，TLE值保持稳定。擦边碰撞前后系统相图如图8(a)、图8(b)和图8(c)所示。可见齿轮副在一个啮合周期内脱啮次数增加一次，相轨迹的拓扑结构未发生改变且冲击状态保持不变。随着Ω的持续减小，系统逐渐由倍周期分岔通向混沌。TLE值突变并大于0，呈震荡上升态势。

由上述分析可知，随着Ω的变化，系统会不断地改变其运动的轨道。而齿面擦边碰撞的发生，有可能会对系统的运动状态(P-Q-R)产生不可预见的影响，改变系统的运动周期和冲击状态。当擦边碰撞发生，TLE值突变时，系统产生分岔，齿轮的运动状态发生较大改变。而当TLE值保持稳定时，系统未出现分岔现象，系统周期数保持稳定但啮合力发生改变，相轨迹可视为向左平移穿过碰撞面而其拓扑结构未发生变化。

3.2 齿侧间隙D对擦边特性的影响

为了保证正常的装配和润滑，齿轮副必须保证必要的齿侧间隙，其大小对擦边碰撞特性会产生一定影响。忽略轴承径向间隙引发的非线性力-位移关系，取基准参数固定为：Fm=0.2,Fah1=0.05，ε=0.2，Ω=1.45，ξ11=ξ22=0.01，ξ13=ξ23=0.012 5，ξ33=0.05，F1=F2=0.1，k11=k22=1.25，无量纲齿侧间隙D∈[0,1.0]。

图9为σ1截面上分岔图。图10为σ2和σ3截面上啮合力F的周期变化图，D<0.171 60时虚线(F=0)以上和以下区域均存在点，系统处于双边冲击状态，D>0.171 60时仅虚线以下区域存在点，系统处于单边冲击状态。图11为最大Lyapunov指数图。

图9 齿轮啮合综合误差x随D变化分岔图Fig.9 The bifurcation diagram of gear comprehensive error of meshing x changing with D

图10 无量纲啮合力F的周期变化图Fig.10 The periodic variation diagram of dimensionless meshing force F

图11 最大Lyapunov指数图Fig.11 The largest Lyapunov exponent

由图9可见，当D∈[0,0.596 40]时，系统为周期1运动，齿面啮合力和齿背啮合力同时存在并且均为1周期。随后系统运动在D=0.059 72和D=0.065 24处发生跳跃且于前一点处发生分岔。跳跃点处TLE值出现突变且近似为零。值得注意的是，D=0.065 24处齿面啮合力突然急剧减小至零附近但未极限接近零，系统处于“2-1-1”运动，为探究此时系统是否发生擦边碰撞，其相图如图12所示。此时，xmin<-D，运动状态和图9、10相互对应，但未存在擦边碰撞的情形。

图12 D=0.065 24系统相图Fig.12 Phase portraits of system in D=0.065 24

当D=0.106 80时，齿背碰撞面发生擦边碰撞(x=-D，齿背碰撞面)，σ3截面上无量纲齿背啮合力F突变为2周期，系统转迁为“2-1-2”运动，TLE值未发生改变。擦边碰撞点前后的相图如图13(a)、图13(b)和图13(c)所示。当D=0.106 10时(图13(a))，相轨迹穿越齿背碰撞面2次，发生1次脱啮。擦边碰撞(图13(b))后，当D=0.107 60时(图13(c)),相轨迹穿越齿背碰撞面4次，发生2次脱啮，但相轨迹拓扑结构未发生改变，系统始终保持双边冲击的状态。

当D=0.121 86时，齿背碰撞面再次发生擦边碰撞(x=-D，齿背碰撞面)并发生分岔，系统发生分岔且TLE值突变至零附近，齿背啮合力F突变为3周期，齿面啮合力F突变为2周期。系统由“2-1-2”向“4-2-3”状态转迁。碰撞前后相图如图14所示。当D=0.120 80时(图14(a))，相轨迹穿越齿背碰撞面4次，发生2次脱啮。相轨迹和齿背碰撞面发生擦边碰撞(图14(b))后，拓扑结构发生变化。如图14(c)所示，相轨迹穿越齿背碰撞面6次，发生3次脱啮。

随后，当D=0.141 00时系统突变至“n-n-n”运动，TLE值突变并大于0，呈高位震荡态势，齿面啮合力和齿背啮合力均突变为长周期。当D=0.172 20时，系统发生边界激变向“4-3-0”转迁。随后，TLE值和系统的运动状态保持基本稳定，系统对齿侧间隙D的变化不再敏感。

综上所述，齿背擦边碰撞会对系统的运动状态产生影响。擦边碰撞发生时，当系统相图未发生拓扑变化且TLE值保持稳定，齿轮副间啮合力改变而周期数保持不变。当相图发生拓扑变化时，系统运动状态改变，特征同前。并且，当齿侧间隙较小时，系统的运动状态较不稳定且存在双边冲击的现象，擦边碰撞现象频繁。当D>0.172 20时，系统发生激变后运动状态保持稳定，齿轮啮合综合误差随着齿侧间隙的改变呈线性变化。