被动变阻尼装置有限元分析、优化设计与试验验证
2022-07-14付伟庆史明妹张春巍
付伟庆, 史明妹, 李 通, 李 茂, 张春巍
(1.青岛理工大学 土木工程学院,山东 青岛 266033;2.蓝色工程区工程建设与安全协同创新中心 青岛理工大学,山东 青岛 266033)
在结构振动控制中,半主动控制减振效果较好,但其实施过程较为复杂,造价较高;被动黏滞阻尼器控制简单有效,但其最优控制范围较窄[1-2]。目前国内外研究主要针对变阻尼TMD、变阻尼隔震支座和位移相关型变阻尼阻尼器以及在传统半主动控制手段上进行改进和创新,对通过机械方式将被动控制系统实现半主动控制的效果未见相关研究[3-7]。
被动变阻尼装置(passive viscous damping device, PVDD)是在普通的黏滞阻尼器基础上研发设计的新型阻尼器。该装置可不需外部能源输入,采用机械方式实时改变阻尼系数,输出可变阻尼力,实现半主动控制的目的,图1和图2分别为被动变阻尼装置的实物图和阻尼阀构造图[8]。
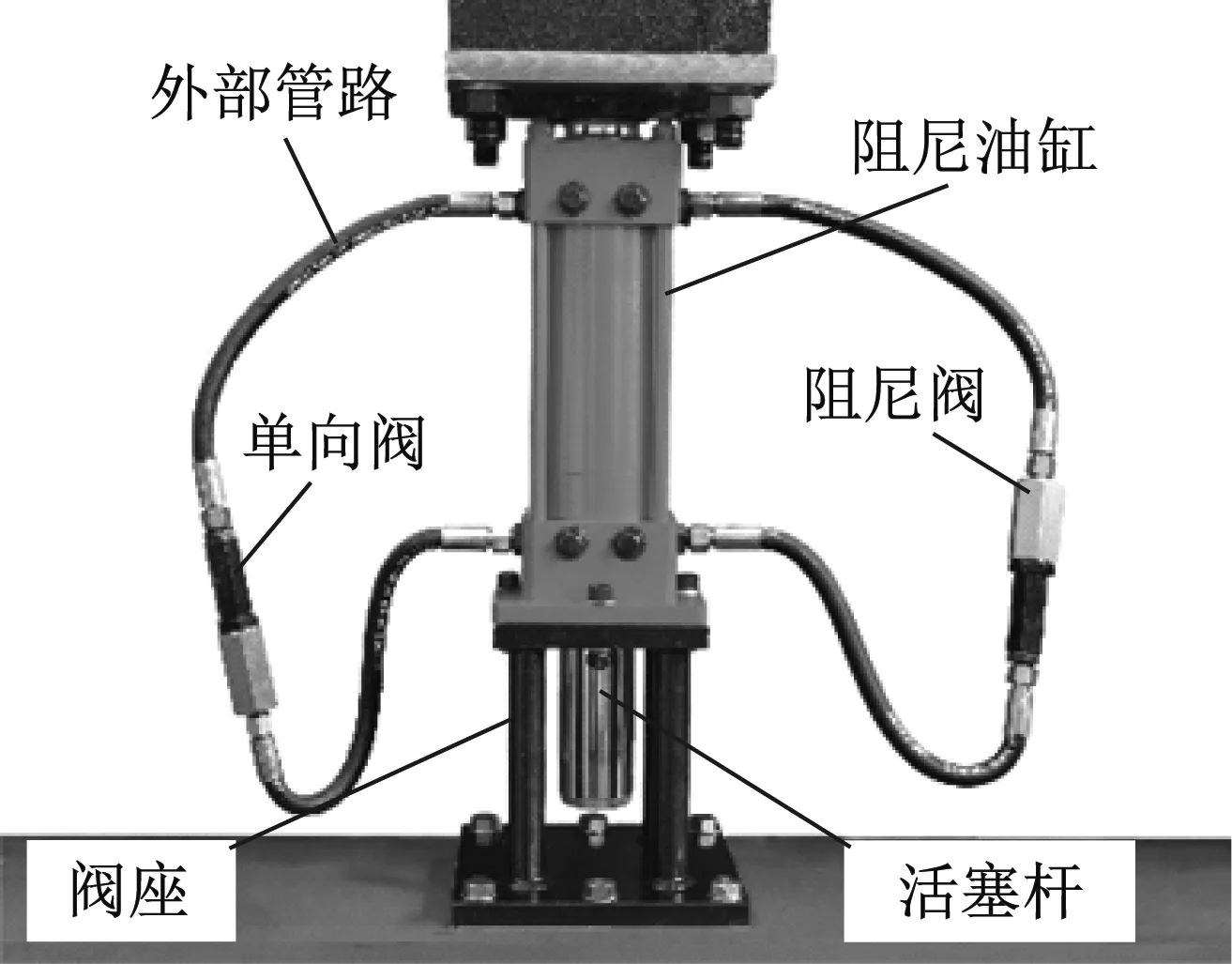
图1 被动变阻尼装置实物图Fig.1 Physical drawing of passive variable damping device

图2 阻尼阀构造图Fig.2 Damping valve construction drawing
被动变阻尼装置(PVDD)工作时,阻尼介质通过外部管道流入控制阀流入口。当外界激励速度增加,缸内的液体压力大于控制阀内的弹簧预压力时,活动阀芯弹簧被压缩,交叉孔的面积开始变小,阻尼器的阻尼系数开始增大,输出的阻尼力不断增大,这就实现了变阻尼的效果。
前期试验中发现,被动变阻尼装置阻尼阀的交叉孔形状对阻尼器出力时程影响很大,不同孔型出力时程存在差异性。另外,装置中组件的尺寸参数对阻尼器最大出力值影响也很大,不同设计参数组合下得到的阻尼器最大出力值不同。阻尼器最大出力和出力时程研究,对该装置的工程应用具有重要意义。
本文在前期被动变阻尼装置初始设计和性能试验的基础上,采用计算流体动力学方法,抽取阻尼器中主要出力构件——阻尼阀部分,对其进行了有限元建模和试验验证,通过计算分析得到阻尼阀不同交叉孔型下的出力时程特点。接着以凸形孔阻尼阀为例,利用正交设计法对影响最大出力的主要因素进行组合计算,得到相同位移条件下最大阻尼力的参数优化组合。最后选取代表性的菱形和倒三角形阻尼阀进行参数计算和分析,通过性能试验验证两种孔型优化设计阻尼器最大阻尼力值的正确性和参数优化方法的有效性。所做研究为被动变阻尼装置的进一步开发与应用提供了良好的理论基础和试验依据。
1 阻尼阀有限元分析及试验对比
1.1 阻尼阀有限元建模与分析
阻尼阀是变阻尼装置的主要构件,也是变阻尼装置的主要出力部分。为简化计算,本文仅对阻尼阀流体进行建模分析,假设模型中的固体材料不发生变形,并将弹簧简化为作用在活动阀芯上的弹性力,因此仿真重点对阻尼阀内部流体进行动网格数值模拟[9]。模拟采用6DOF模型,并根据UDF手册编写UDF程序,设定活动阀芯重心位置坐标、弹簧刚度,弹簧预压力值为重心坐标位置和实际位置坐标的差值与弹簧刚度的乘积。由于模型的对称性,采用四分之一模型进行计算并设置对称边界条件,采用ANSYS软件进行分析,流体网格模型如图3所示。表1为流体和弹簧的参数设置。

图3 阻尼阀流体网格模型图Fig.3 Damping valve fluid mesh model diagram

表1 流体和弹簧参数Tab.1 Liquid and spring material properties
根据流量等效原则,将活塞杆的运动速度转化为阻尼阀入口流体速度[10]
Ac·vc,max=(Acy-Arod)·vmax
(1)
式中:Ac为阻尼阀入口截面面积;vc,max为节流阀入口处流体的流速;Acy为阻尼油缸的截面面积;Arod为活塞杆截面面积;vmax为活塞杆运动速度。
1.2 阻尼力计算公式推导
由于被动变阻尼装置的阻尼出力除阻尼阀外还有阻尼油缸、外部管路和单向阀,阻尼油缸产生的阻尼力较小,在此处忽略不计,对外部管路和单向阀阻尼力进行单独计算。
外部管路产生的阻尼力根据达西阻尼公式[11]
(2)
式中:hf是沿程阻力损失;λ是水头损失系数;l是管道长度,d是管道内径,v是管道流速,g是重力加速度。其中,
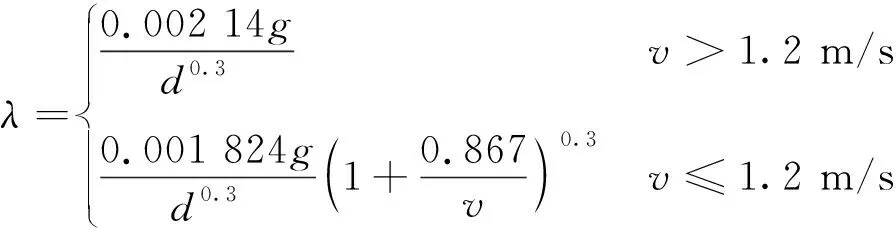
(3)
单向阀的压力损失根据流量关系式进行计算[12]
(4)
式中:Q是单向阀液体流量;C是流量系数;A是流通面积;ΔP是压力损失;ρ是液压油密度。
因此,阻尼器产生的阻尼力F由三部分组成,其中,Fval为阻尼阀产生的阻尼力
F=hf+ΔP+Fval
(5)
1.3 有限元阻尼力计算与性能试验对比
模型计算采用与试验相同的加载机制及模型参数,根据试验工况,分别对圆形、倒三角形孔型阻尼阀进行有限元计算,为对被动变阻尼装置的耗能能力和变阻尼趋势进行验证,本文选取阻尼力-位移曲线将模拟结果与试验结果进行对比,装置试验研究参见文献[13]。图4为试验所用交叉孔型示意图,表2为试验加载工况及模型参数。部分工况对比结果如图5所示。
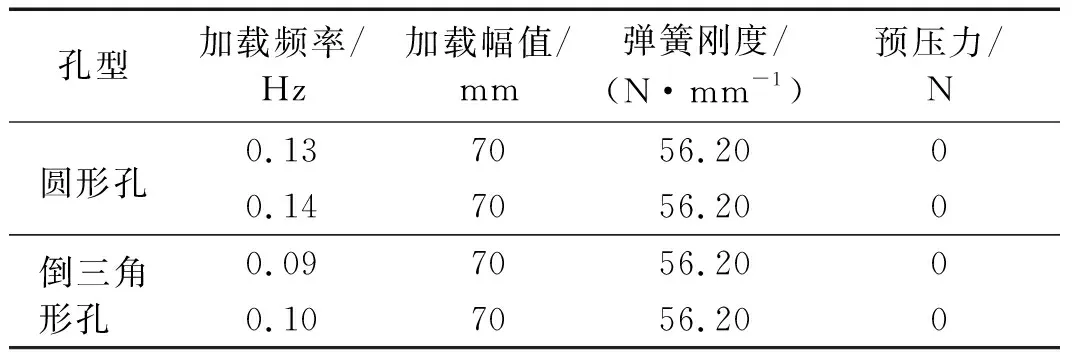
表2 试验加载工况及模型参数Tab.2 Experimental loading conditions and model parameters
针对仿真模拟与试验得到的最大阻尼力之间的误差进行了对比,具体的误差值见表3。
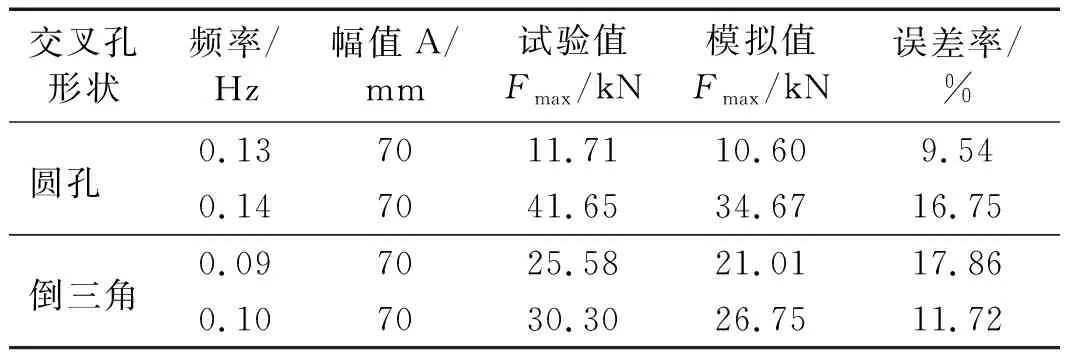
表3 误差分析表Tab.3 Error grid analysis
通过对模拟与试验的对比分析可以看出,两种孔型模拟计算结果与试验曲线趋势吻合较好,最大阻尼力误差为17.862%,一般工程应用中,试验与数值模拟的误差允许在20%以内是可以接受的,因此对比结果的最大误差满足要求。试验得到的滞回曲线表现为左右不对称,力最大值并不位于位移为零位置处,模拟计算表现相对对称性。差别原因在于试验具有时滞性而模拟没有时滞性,试验表现出的时滞性是由于液体黏度的存在而表现出来的滞后性,该滞后性会对结构的控制效果产生影响,对被动变阻尼装置的出力过程和阻尼力的大小无影响,减小时滞性的影响将在后续进行研究。
试验曲线上下相对不对称,是由于加工误差使活动阀芯与固定阀芯之间的摩擦程度不同,在相同的流体力作用下活动阀芯位移程度不同,导致滞回曲线上下两侧的最大出力不同。通过提高试件加工的精度可以减小该误差。
尽管数值计算结果和试验曲线存在一些差异性,但最大出力与试验结果接近,阻尼力变化趋势也较为接近,证明有限元建模和模拟方法的正确性,这为后续的参数分析及优化设计奠定了基础。
2 阻尼阀孔形对出力影响的有限元分析
2.1 不同交叉孔形阻尼阀设计
为初步探究不同交叉孔型对出力过程的影响,在装置有限元模型验证的基础上,且为便于加工制造,设计菱形、正三角、凸形、矩形、圆形、倒三角六种交叉阻尼孔型,进行装置不同阻尼出力过程和最大出力的计算分析。交叉孔初始面积均为23.75 mm2,交叉孔的长度设为5.5 mm,为确保模拟对比过程中因素分析的唯一性,且保证实际操作的安全性,将活动阀芯最大位移设置为4.6 mm,入口速度采用频率f为0.14 Hz,幅值A为70 mm,模拟分析过程中参数设置及过程均与上述验证模拟过程相同。图6为倒三角形和菱形交叉孔活动阀芯与固定阀芯装配设计实物图。
2.2 交叉孔形对出力影响有限元分析
针对设计出的几种孔型阻尼阀进行综合分析,图7给出了几种交叉阻尼孔变阻尼装置的滞回曲线。图8为不同交叉孔型交叉孔面积与阻尼力关系曲线。

图8 阻尼阀交叉孔面积与阻尼力关系Fig.8 Relationships between cross orifice area of damping valve and damping force
在最大阻尼力值方面,从滞回曲线图看出不同交叉孔的最大出力值不同。倒三角形阻尼阀的最大出力是其它交叉孔形状两倍多。从速度与阻尼力关系曲线中看到,倒三角孔阻尼力突变速度最小,菱形孔阻尼力突变的速度较大。在阻尼出力时程方面,在相同的加载速度下,倒三角和菱形孔型是阻尼系数变化最为剧烈的,但倒三角的阻尼力值大于菱形孔;圆形、矩形、凸形和正三角形交叉孔阻尼系数变化则比较平缓。原因在于被动变阻尼装置的出力大小与交叉孔的面积相关,而不同的交叉孔型在相同的速度下交叉孔剩余面积和剩余面积变化率不同,这就导致不同的孔型阻尼出力峰值和阻尼系数突变速度的不同。
针对不同交叉孔型出力时程和阻尼力峰值的不同,可在实际情况中选择不同的交叉孔型。倒三角和菱形阻尼阀阻尼系数变化比较大,适用于要求阻尼力变化比较剧烈的情况,且倒三角的适用于阻尼力要求较大的场景。圆形、凸形、矩形、正三角孔阻尼力随速度变化比较平缓,其阻尼系数变化比较小,这些孔型适于要求阻尼出力变化比较平缓的情况。
图8表示了交叉孔剩余面积与产生阻尼力之间的关系,随着交叉孔面积的减小,阻尼力在不断增加。各种孔型阻尼力随着交叉孔剩余面积的变化趋势与图7中阻尼力产生趋势是相同的,并且不同交叉孔型的阻尼力时程变化与图7中阻尼系数变化呈现相同的趋势,这说明被动变阻尼装置阻尼力峰值大小是交叉孔剩余面积决定的,而不同交叉孔型呈现出不同的时程特点,则是由于不同交叉孔面积变化率所导致。交叉孔剩余面积与阻尼力的关系解释了不同交叉孔型阻尼力峰值与阻尼系数变化趋势不同的原因。
3 装置最大出力影响因素分析和设计参数优化
以凸形孔阻尼阀为例,利用正交设计表划分影响装置最大出力的因素和水平,通过计算确定影响装置最大出力的主要因素[14-15]。再通过对这些影响因素的组合分析,得到相同位移条件下最大阻尼力值的最优参数组合。
3.1 最大出力影响因素分析
影响阻尼出力大小的因素有流入孔的半径、流入口的长度、弹簧的刚度和预压力和交叉孔的形状等。弹簧的刚度和预压力主要体现在活动阀芯的位移上,可将两者看成活动阀芯位移大小对阻尼出力的影响。
正交设计根据正交性从全面试验中挑选出部分有代表性的点进行试验,具有“均匀分散,齐整可比”的特点。利用正交设计表L25(56)计算确定各因素对装置最大出力的影响程度,因素水平表见表4。

表4 因素水平表Tab.4 Factor level table mm
在直观分析的基础上进行方差分析,构造F统计量,生成方差分析表,对因子主效应做检验。表5和表6分别是阻尼出力的方差分析表和剔除最不显著影响因素的影响阻尼出力的方差分析表。
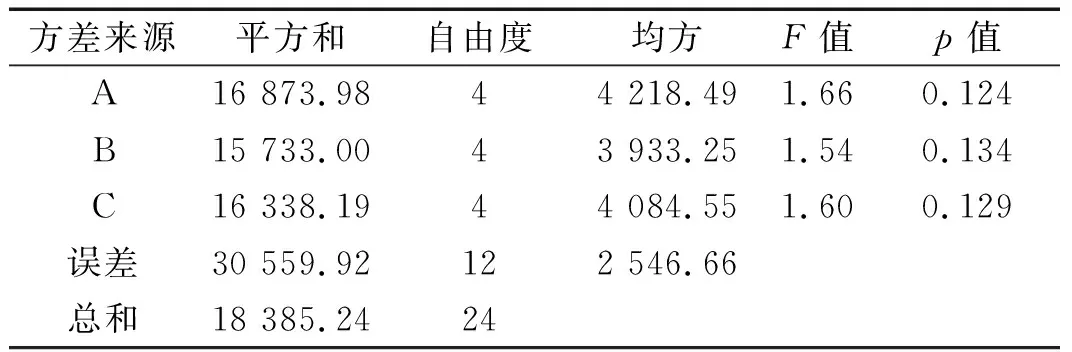
表5 阻尼出力方差分析表Tab.5 Variance analysis table of damping force
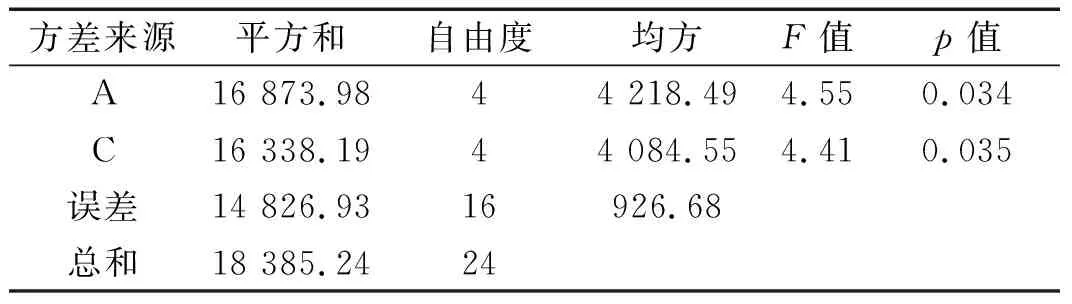
表6 剔除B后阻尼出力方差分析表Tab.6 Variance analysis table of damping output after eliminating B
从方差分析表中可以看到三个因子的p值均大于0.05,剔除一个最不显著的因子B重新做方差分析,见表6。
新得到的方差分析表中A(入口半径)因子的p值=0.034<0.05,是最显著的,说明A(入口半径)因子是影响阻尼出力的主要因子;C(阀芯位移)因子的p值=0.035<0.05,说明它也是影响阻尼出力的主要因子,但次于A因子。因此三个因素对阻尼出力的影响大小排序为A,C,B。
经具有科学统计依据的方差分析得到的结果与直观分析得到的结果一致。由模拟结果看出变阻尼装置最佳水平组合是A1B5C5,也即流入口半径越小,长度越长,活动阀芯位移量越大,装置产生的阻尼力越大。将A1B5作为适合已有阻尼器最优出力阻尼阀尺寸(以下简称最优组合),将A3B3看做阻尼阀的普通尺寸组合(以下简称一般组合)。
3.2 最大出力值最优参数组合
选取出力变化较大的倒三角和菱形孔型,结合正交分析提取的主要影响因素,对两种孔型进行最优参数组合计算,并将最优组合与一般组进行对比分析。在相同的入口速度下,计算结果如表7、8和图9所示。

表7 倒三角模拟工况及结果Tab.7 Inverted triangle simulation conditions and results
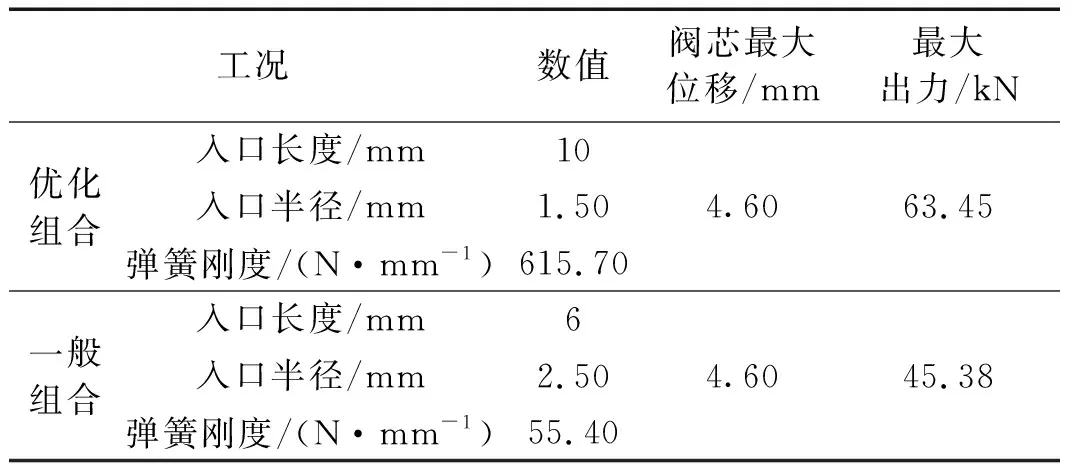
表8 菱形模拟工况及结果Tab.8 Rhombus simulation conditions and results
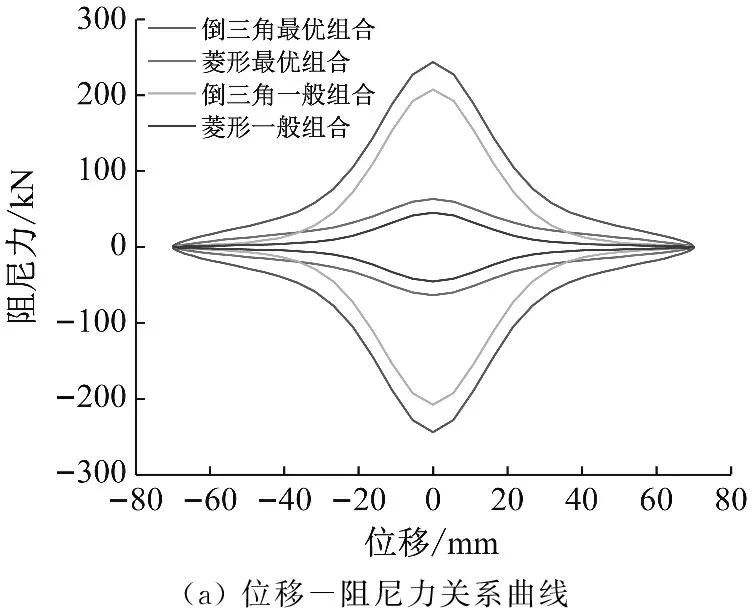
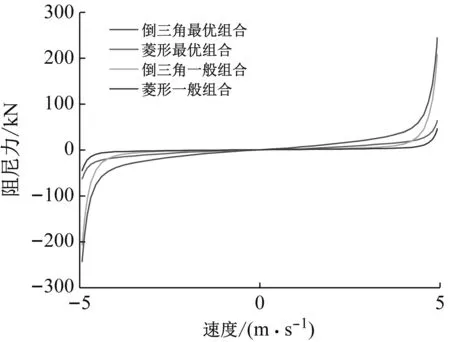
(b) 速度-阻尼力关系曲线图9 菱形、倒三角阻尼阀滞回曲线图Fig.9 Hysteretic loops of diamond-shaped and inverted triangular damper valves
从上述图表中可以看出,采用优化组合的变阻尼装置的滞回曲线明显比一般组合更为饱满,且最大出力也相对更大;在相同的速度,相同的活动阀芯位移下,最优组合的最大出力更大;最优组合阻尼力突变的速度相对于普通组合的速度更大。
按相同优化计算过程,可得到其它孔型节流阀相同活动阀芯位移下,最大阻尼出力的最优参数组合。限于文章篇幅,不再列出。
4 装置优化设计最大阻尼力值的试验验证
对优化参数设计前后装置的最大出力值,通过性能试验进行验证和优化效果对比。
4.1 装置性能试验简介
试验在青岛理工大学结构实验室进行,采用正弦位移u(t)=Asin(2πft)加载机制,加载速度为v(t)=2πfAcos(2πft),其中,f为加载频率,A为加载幅值。被动变阻尼装置试验按照加载幅值为40 mm、50 mm、60 mm、70 mm,加载频率选取范围为0.02~0.3 Hz,从小到大逐级递增进行加载,加载频率与加载幅值的组合值作为被动变阻尼装置的加载速度,该组合速度范围基本可涵盖结构所需。试验通过更换不同形状的阻尼阀,得到不同的交叉阻尼孔形状控制被动变阻尼装置的出力过程和大小。试验装置采用的各种交叉孔孔型初始面积相同,且初始交叉孔长度为5.5 mm,为保证试验过程的安全性,将节流阀试件最大的位移设置为4.6 mm。图10为试验过程图。

图10 试验中装置图Fig.10 Diagram of device in test
4.2 优化设计阻尼器性能试验和优化效果对比
图11为倒三角交叉孔型阻尼器优化前后设计参数组合位移与阻尼力关系部分试验对比结果。图12为优化前后速度与阻尼力关系试验结果对比图。
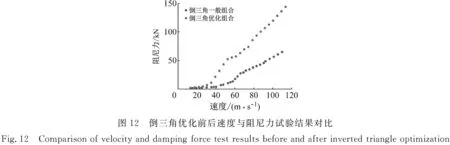
从图11和图12中可见,优化参数后的被动变阻尼装置相比于优化前组合具有更好的耗能性能。在相同的加载频率和试验条件下,优化设计后被动变阻尼装置提供的最大阻尼力明显大于未优化下,这证明了优化过程计算的正确性和优化方法的有效性。
为验证优化结果及方法的准确性,将相同条件下阻尼出力较大的倒三角和菱形交叉孔孔型的最优组合进行试验,并将试验结果与模拟结果进行对比,由于篇幅限制,只选取部分频率进行对比,图13为两种孔型的模拟和试验对比结果。
从图13中看出,优化模拟结果与试验结果吻合较好,两者在最大阻尼力与阻尼力的变化趋势大致相同,进一步证明优化结果和方法的准确性。本次优化结果及方法为被动变阻尼装置后续的研究及应用提供了理论基础。
5 结 论
(1) 被动变阻尼装置简化有限元模型的计算值与试验结果吻合度较好,证明了建模过程和仿真模拟方法的正确性。
(2) 设置不同孔型的阻尼阀装置出力时程特点不同。倒三角和菱形孔阻尼阀适用于要求阻尼力大,阻尼力变化比较剧烈的情况;圆形孔阻尼阀适用于要求阻尼力变化平缓且阻尼力比较大情况;凸形、矩形、正三角孔阻尼阀适用于要求阻尼力小,且变化比较平缓的情况。
(3) 通过正交设计法确定了影响装置最大出力值的主要因素,并计算出相同位移条件下最大出力值影响因素的最优参数组合。
(4) 通过被动变阻尼装置的性能试验,验证了优化设计参数后阻尼器最大出力值的正确性。与一般参数组合阻尼器试验值的对比,证明了该设计参数优化方法的有效性。
