旋转输流管中管结构强迫振动的格林函数解
2022-07-14范谨铭常学平
范谨铭, 常学平, 陈 美
(西南石油大学 机电工程学院,成都 610500)
输流管结构在航空航天、石油工业、海洋工程等领域有着广泛的应用,在内流的作用下会使得结构发生流固耦合振动,容易引起结构失效。作为最为典型的流固耦合结构,输流管系统的自由振动与强迫振动问题引起众多学者的关注[1-4]。
Ni等[5]将微分变换法推广至几种典型边界条件下输流管道的自由振动问题,将得到的系统固有频率和临界流速与微分求积法的结果进行了比较,验证了方法的可靠性。基于挠度的多项式逼近,Khudayarov等[6]将含脉动内流的流致振动问题归结为一个常积分-微分方程组的研究,并用数值方法求解。赵千里等[7]利用伽辽金法研究了层流模型和平推流模型对输流管系统固有频率及临界流速的影响。应用一种改进傅里叶级数方法,不同边界的梁模型与输流管系统的横向振动问题被进行了研究,且该方法具有收敛快、精度高的特点[8-10]。Lannes等[11]通过试验研究了内流为双相流时输流管的强迫振动问题,并且讨论了含气率与系统响应的关系。
然而,工业中的输流管结构往往是更加复杂的,例如旋转输流管结构、管中管结构等。这些耦合系统的动力学特性受到诸多因素的干扰,研究难度会大大增加。因此针对非常规输流管结构的研究成为近些年的热点。
Wang等[12]以两端简支的双壁碳纳米管为例,研究了各参数对结构稳定性的影响,发现内外管间材料的弹性系数对临界流速有着显著的影响。Bi等[13]对管中管结构的减振功能进行了验证,发现该结构在控制各种因素引起的海底管道的振动方面有很大的潜力。旋转输流管在旋转运动和流固耦合陀螺效应的综合影响下,可以被视为双陀螺系统[14]。Lian等[15]建立了水平井非线性钻柱的动力学理论模型,讨论了旋转速度、钻压频率等因素对系统的影响。Chang等[16]研究了气体钻井中钻柱在气体结构相互作用下的振动特性,发现气体钻井钻柱的固有频率比泥浆钻井钻柱的高。
在求解输流管模型的动力学问题时,格林函数法是一种极为方便的方法,此方法不仅可以得到系统闭合形式的响应解,也可被用来研究系统的频率问题[17]。Li等[18]采用格林函数法给出了具有不同边界条件的输流管道受迫振动的格林函数解,并通过三个算例验证了方法的有效性。Zhao等[19]将该方法应用于输流曲管中,研究了不同参数对系统切向位移和径向位移的影响。借助双参数地基上输油管道强迫振动的格林函数,Li等[20]讨论了边界弹簧系数对输流管系统稳定性的影响,结果表明系统的自振频率和临界流速与边界条件有很大的关系。
综上所述,格林函数法的突出优点是能够获得系统强迫振动响应的解析解,具有极高的精确性和可靠性。但尚未有学者得到旋转管中管(PIP)耦合系统强迫振动的格林函数解。因此本文建立了输送双相内流的旋转管中管(PIP)结构横向强迫振动的控制方程,并依次采用分离变量法、Laplace变换和Laplace逆变换得到系统的格林函数。对模型的控制方程进行解耦将会得到单管模型、旋转管道模型及无旋转管中管结构的格林函数。在数值讨论部分,首先验证本文方法的可靠性,然后以悬臂结构为例,研究不同参数对格林函数的影响,研究结果为旋转管中管结构的动力学设计提供了理论依据。
1 旋转PIP系统控制方程的建立
图1为输运气-液双相流的旋转PIP系统的力学模型,由长度均为L的外管、内管以及两管之间的保温层组成。内管中含有水平流动的双相流,UL、UG分别表示液相流速和气相流速。根据力学性能将保温层简化为沿着管长方向分布的弹簧阻尼系统,且刚度系数为K,阻尼系数为C。为了便于识别,角标i、o被用来区分内管和外管的参数。内管的内外径分别为di、Di,外管的内外径分别为do、Do。在系统的左侧给出了系统的坐标系,其中O为原点坐标,z代表轴向方向,x和y表示两个垂直的横向方向。在轴向内管受到轴向压力Ni的作用,外管受到轴向压力No的作用,在Oxz平面内,外管受到指向y方向的均布载荷P(z,t)的作用,同时内管和外管绕z轴匀速转动,转速均为Ω。

图1 含双相流的旋转PIP系统的力学模型Fig.1 Mechanical model of spinning PIP system with two-phase flow
1.1 系统的动能
用i、j、k分别表示沿着x轴、y轴和z轴的单位矢量,则内管和外管上某一点的位移矢量ri、ro的表达式为
(1)
式中:u1、u2表示内管任一点在x方向和y方向的位移;u3、u4为外管上任一点在x方向和y方向的位移;uz1、uz2分别表示内外管在z方向的位移。
因此内管与外管上任意一点的速度矢量表示为
(2)
在当前的研究中,不考虑内部双相流随系统的转动,因此液相和气相的速度矢量形式为
(3)
旋转管中管系统的动能由内管的动能T1、外管的动能T2、液相的动能T3及气相的动能T4组成,它们的表达式分别为
(4a)
(4b)
(4c)
(4d)

根据Lannes等的双相流滑移因子模型,得到气体体积分数ε、空化率α和滑移因子Ke的表达式为
(5)
式中:CG和CL分别表示单位长度管内气相和液相的体积;QG和QL表示相应的体积流量。因此在式(4)中,mG=ρGCG,mL=ρLCL,其中ρG和ρL分别为气相和液相的密度。
此外,在双相流滑移因子模型中,气体体积分数ε和滑移因子Ke的关系为
(6)
根据式(2)和(3),单位长度管内的气相的质量mG和气相流速UG可以表示为
(7)
综上,旋转PIP系统的总的动能T表示为
T=T1+T2+T3+T4
(8)
1.2 系统的势能
在本文的研究中,系统的势能包含内管的应变能U1、外管的应变能U2、保温层的等效弹簧的弹性势能U3及等效阻尼器的耗散能U4,它们的表达式为
(9a)
(9b)
(9c)
(9d)
式中:Ei、Eo分别为内管和外管的杨氏模量;Ii、Io分别为内管和外管的截面惯性矩。
因此,系统的总势能U可表示为
U=U1+U2+U3+U4
(10)
1.3 系统的外力功
旋转PIP系统所受的外力有轴向压力Ni、No,以及横向的均布载荷P(z,t)。因此,系统的外力功可以表示为


(11)
1.4 系统的控制方程
采用广义哈密顿变分原理进行控制方程的建立,其表达式为
(12)
将式(8)、(10)、(11)代入式(12),经过化简计算得到了旋转PIP系统的四个控制方程,按顺序分别为内管在x方向、内管在y方向、外管在x方向及外管在y方向的控制方程,表示如下
(13a)
(13b)
(13c)
(13d)
为了使得计算变得简洁,引入以下无量纲量
(14)
将式(14)代入旋转PIP结构横向振动的控制方程中,得到了考虑双相流及轴向压力的旋转PIP系统的无量纲控制方程为
(15a)
(15b)
(15c)
(15d)
在表1中给出了本文模型的几种无量纲的边界类型,其中η用来指代管中管系统的无量纲位移η1、η2、η3和η4,撇号代表对无量纲位置ξ的微分。

表1 模型的几种边界条件Tab.1 Several boundary conditions of the model
2 格林函数法求解
2.1 PIP系统的格林函数解
在本文的研究中,横向外力为简谐力,即
p(ξ,τ)=q(ξ)eiωτ
(16)
式中,ω为无量纲外激频率。
旋转PIP系统的控制方程,即式(15)的解可以表示为以下形式
η1(ξ,τ)=X1(ξ)eiωτ,η2(ξ,τ)=X2(ξ)eiωτ
η3(ξ,τ)=X3(ξ)eiωτ,η4(ξ,τ)=X4(ξ)eiωτ
(17)
将式(17)代入式(15),化简后可得
(18)
式中,系数aj、bj、cj、dj(j=1,2,3,4)的表达式为
(19)
根据格林函数的定义,可知式(18)的格林函数解与下式相同
(20)
式中,δ(·)为狄拉克函数。
获得系统横向振动的格林函数的方法有很多,拉普拉斯变换及拉普拉斯逆变换是较为便捷的一种。对式(20)中的无量纲位置变量ξ进行拉普拉斯变换,整理可得相应得象函数为

(21a)

(21b)
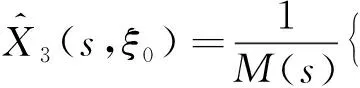
(21c)

(21d)
式中,λmn(m=1,2,3,4;n=1,2,3,4)为M(s)的m行n列的代数余子式。M(s)的表达式为
(22)
其中,M1、M2、M3和M4的表达式如下
(23)
通过对式(21)执行拉普拉斯逆变换,便得到了相应的四个格林函数Gm(ξ,ξ0)(m=1,2,3,4)为
X‴4(0)Φm16(ξ)+Φm16(ξ-ξ0)H(ξ-ξ0)
(24)
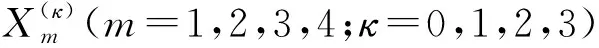

利用所求得的四个格林函数及线性叠加原理,便可求得旋转PIP系统强迫振动内外管在x方向和y方向的响应解ηm(ξ,τ)(m=1,2,3,4)为

(25)
2.2 格林函数中未知系数的计算
利用表1中不同的边界条件,可以求出相对应的格林函数解的未知参数。利用旋转PIP系统的格林函数解Gm(ξ,ξ0)(m=1,2,3,4)对无量纲位置坐标ξ的第一~三阶导数,并取ξ=1,整理得到下式
(26)
式中,Qmn(m=1,2,3,4;n=1,2,3,4)均为四行四列的矩阵,它们的表达式如式(27)所示;Xm(m=1,2,3,4)为左边界条件列阵,Gm(m=1,2,3,4)为右边界条件列阵,fm(m=1,2,3,4)为外激励项列阵,它们的表达式在式(28)中给出。
(27a)
(27b)
(27c)
(27d)
(28a)
(28b)
(28c)
式中,Ψ=1-ξ0。
根据表1将所对应的边界条件代入式(25),经过化简计算便得到了式(24)相对应的格林函数中的未知左边界系数。将求解得到的左边界系数和已知的边界条件代入式(24),便得到了完整的旋转管中管系统的四个格林函数解。
3 数值结果及讨论
本文所研究的PIP系统的相关参数为:长为L=10 m,内管的内径为di=0.16 m,内管的外径为Di=0.22 m,外管内径do=0.22 m,外管外径Do=0.26 m,内、外管的弹性模量均为2×1011N/m2,密度均为7 850 kg/m3,液相内流密度为ρL=1 000 kg/m3,气相内流密度为ρG=1.2 kg/m3。
3.1 解的有效性验证
本小节忽略保温层的作用和旋转的影响,通过解耦得到了无旋转输流管横向振动的动力学模型。利用格林函数法求解了两端都为简支边界的输流管模型的横向振动。验证部分结构模型及材料属性的相关参数取自于马腾等,无量纲参数βi的取值为0.5,内流取为单相流,并取三组无量纲内流流速uL分别为0、1和2。通过改变外激频率ω,得到了三种无量纲内流流速下,在0.7位置处作用单位简谐载荷时0.1处的幅频曲线。图2给出了在三种内流流速下前三阶无量纲固有频率曲线规律,其具体数值在表2中给出。通过与马腾等采用改进傅里叶法得到的结果进行对比,可以发现采用本文的方法得到的结果与参考文献基本一致。两种方法存在误差的原因主要是马腾等采用的改进傅里叶法存在截断误差,在求解系统的频率时会与精确解产生明显的误差。而本文的格林函数法得到的解为精确的解析解,更精确与可靠。

表2 具有不同内流流速的模型的无量纲频率Tab.2 Dimensionless frequencies of models under different boundaries
3.2 不同参数对无旋转PIP系统的影响
本小节以不旋转的悬臂PIP系统为研究对象,研究气体体积分数、轴向压力、内流流速及弹簧刚度系数对系统格林函数基础响应的影响。
图3展示了外激励频率为ω=20时,含有不同气体体积分数的无旋转悬臂管中管系统的格林函数解。计算时的相关无量纲参数为k=300、c=2、uL=3、pi=0、po=0。设置了三组气体体积分数分别为0、0.4和0.8,且力的作用点为ξ0=1。由于无旋转系统的响应只会在受力的y方向产生,表示x方向响应的G1(ξ,1)与G3(ξ,1)都为0,因此不在图中给出。从图中可以看到,在内流的作用下,此时内管与外管在x方向的格林函数基础响应G2(ξ,1)与G4(ξ,1)的响应是呈整体相反趋势的。随着气体体积分数的增大,G4(ξ,1)在靠近固定端的一侧几乎不变,在靠近自由端的一侧逐渐增大。而G2(ξ,1)在ξ小于7.8时,随着气体体积分数的增大响应逐渐增大,在靠近自由端时表现出相反的规律。

图3 具有不同气体体积分数的无旋转悬臂PIP系统的格林函数Fig.3 Green’s functions of non-spinning cantilever PIP system with different gas volume fractions
图4所示为无量纲弹簧刚度系数分别为0、100、200的无旋转悬臂PIP系统横向强迫振动的格林函数解G2(ξ,1)与G4(ξ,1)。为了使得结果对比清晰,忽略了阻尼、轴力及流速的影响,即取c=0、uL=0、pi=0、po=0、uL=0、εG=0。并且设置了三组无量纲弹簧刚度系数分别为0、100、200,无量纲外激频率取为30。从图4中可以清楚地发现,在此条件下,随着弹簧刚度系数的增大,外管的响应逐渐减小,而内管的响应逐渐增大。

图4 具有不同刚度系数的无旋转悬臂PIP系统的格林函数Fig.4 Green’s functions of non-spinning cantilever PIP system with different stiffness coefficients
图5给出的是无旋转悬臂PIP系统施加不同的外管轴向压力po时的格林函数解G2(ξ,1)和G4(ξ,1)。计算时,其他的无量纲参数为k=200、c=2、uL=0、pi=0、εG=0,且此时的无量纲外激频率为ω=20。三组无量纲外管轴力为0、4、8,随着轴力的改变,内管与外管在y方向上的格林函数解也随之发生变化。从图中可以发现,在该条件下,随着外管轴向压力的增大,内管自由端的响应随之增大。而外管表现的较为复杂,在靠近固定端一侧响应随着外管轴向压力的增大而减小,在自由端是先减小后增大。

图5 具有不同轴向压力的无旋转悬臂PIP系统的格林函数Fig.5 Green’s functions of non-spinning cantilever PIP system with different axial pressures
图6表示了液相流速uL分别为0、2、4时无旋转悬臂PIP系统强迫振动的格林函数解G2(ξ,1)与G4(ξ,1)。计算时无量纲外激频率为ω=30,而其他相关参数的取值分别为k=200、c=2、pi=0、po=0、εG=0。随着流速的变化,内外管受力向的格林函数解也相应地发生变化。其中内管受流体直接的作用,在固定端一侧响应随着流速的增大而减小,而在自由端一侧,流速为0和2时几乎相同,当流速继续增大为4时才表现出不同的形式。由于弹性层的作用,外管也会受到内流的影响,其格林函数解在固定端一侧随着流速的增大而增大,而在自由端一侧则是随着流速的增大而减小。

图6 具有不同内流流速的无旋转悬臂PIP系统的格林函数Fig.6 Green’s functions of non-spinning cantilever PIP system with different flow velocity
3.3 旋转速度与内流流速的综合影响
本小节考虑了旋转的影响,讨论了旋转速度和内流流速对外激频率为ω=10时的系统的强迫振动的格林函数解的影响。计算时,不考虑轴向压力、气体体积分数、弹簧刚度系数等因素的影响,相关无量纲不变量取为k=300、c=2、pi=0、po=0、εG=0。无量纲液相流速uL的范围为0~1,无量纲旋转速度Ω*的取值范围为0~20。结果在图7中以云图的形式表示。
图7表示了此时条件下管中管结构ξ=1点受单位简谐力时ξ=1处的格林函数响应解的响应云图。其中G1(1,1)和G3(1,1)分别表示内管和外管在x方向的基础响应,而G2(1,1)和G4(1,1)分别表示内管和外管在y方向的基础响应。从图7(a)和图7(b)中可以看到,内管产生了复杂的响应,这种现象归因于内外管的相互作用,式(13a)和(13b)中弹性层的刚度项和阻尼项使系统内外管产生耦合作用。从图7(c)和图7(d)中可以看到,当有转速存在时,虽然系统的受力方向为y方向,但是由于旋转耦合作用的影响,系统在x方向也会产生较大的响应,这个现象是由方程(13c)和(13d)中的旋转科氏效应引起的。此外,从图中可以清楚地看到,在低流速且无量纲旋转速度Ω*在7或13附近时,内、外管的两个方向上会产生较高重合度的共振带,且转速和流速的变化会影响共振区间。从方程(13)中可以看出,由于内外管x和y方向的旋转科氏力项符号相反,系统固有频率会出现分岔,且旋转速度和内流流速会改变系统刚度,进而使得系统的固有频率发生变化;当外激频率接近管中管结构中内管或外管某一个方向的固有频率时,系统就会发生共振。在内管或外管某一方向上发生共振时通过弹簧层的作用使得其他方向上产生了较大的响应,进而会影响系统的正常工作,降低结构的可靠性,引起结构的失稳与破坏。因此,在工程中需要避免接近图7中所示的共振带。
4 结 论
本文建立了计入气-液双相流和轴向外载的旋转管中管结构的动力学模型,采用格林函数法进行了求解,得到了适用于各种边界条件的旋转管中管结构横向振动的格林函数。根据线性叠加原理,得到了旋转管中管结构横向强迫振动响应的解析解。本文的结果同样适用于具有不同边界条件的无旋转单管、无旋转双管及旋转单管结构的横向强迫振动问题的研究。在数值分析与讨论部分,利用格林函数法得到以下结论:
(1) 通过格林函数幅频特性曲线获得了具有不同内流流速的无旋转输流管模型的前三阶固有频率。经过与参考文献的结果的对比,验证了格林函数解的高精确性和本文方法的可靠性。
(2) 以悬臂管中管结构为例,讨论了气体体积分数、内流流速、弹簧刚度系数和轴向压力等对无旋转管中管结构的格林函数响应的影响。在本文所取的条件下,随着气体体积分数的增大,内外管自由端的格林函数响应均减小;随着轴向压力或内流流速的增大,内外管自由端的格林函数响应均增大;随着弹簧刚度系数的增大,内管自由端的格林函数响应增大,而外管自由端的格林函数响应减小。
(3) 当无量纲外激频率为10时,在关于流速和转速的格林函数云图中,发在现内外管的两个横向振动方向上会产生较高重合度的响应带。且当Ω*在7或13附近且uL小于1时,管中管结构会产生显著的共振现象。工程中需要选取远离共振带的的转速与流速以避免产生过大的响应,以免引起结构的破环。
