圆柱阵特征波束分解与综合超指向性波束形成方法

朱少豪, 杨益新, 汪 勇



圆柱阵特征波束分解与综合超指向性波束形成方法

朱少豪, 杨益新, 汪 勇

(西北工业大学 航海学院, 陕西 西安, 710072)

为了将较小尺寸兼顾较高空间指向性的传感器阵列应用于空间受限的水下无人系统等平台上, 文中采用超指向性波束形成方法以提高小尺寸传感器阵列的空间指向性和阵增益, 从而改善阵列的目标探测性能。首先介绍了基于特征波束分解与综合(EBDS)的圆环阵超指向性波束形成方法, 然后提出了圆柱阵在任意俯仰角方向分两级子阵波束形成的数学模型, 并推导了各向同性空间均匀噪声场中的圆柱阵噪声互谱矩阵。圆柱阵波束图和阵增益的仿真结果表明, 文中提出的方法在低频段的指向性和阵增益远高于常规波束形成方法, 其拓展了EBDS方法的适用范围, 增强了圆柱阵的探测性能, 为小尺寸阵列进一步应用到低频水下无人系统探测中提供参考。

水下无人系统; 超指向性; 特征波束分解与综合; 圆柱阵

0 引言

在自主水下航行器(autonomous undersea vehicle, AUV)、遥控水下航行器(remotely operated vehicle, ROV)等水下无人系统中, 常常需要声传感器(水听器)阵列进行目标探测、识别、定位和跟踪以及水下通信等任务[1-2]。由于小型水下无人系统平台空间有限, 水听器阵列的尺寸受到了限制, 但信号处理中的常规波束形成(conventional beamforming, CBF)往往需要较大尺寸的阵列才能获得较为理想的结果。针对这个问题, 超指向性波束形成方法给出了解决方案, 它能够在不改变阵列尺寸的情况下提高空间指向性和阵增益, 并且具有频率不变响应等优点。

经过多年发展, 人们提出了多种超指向性方法以满足不同阵型的需要。由Capon[3]于1969年提出的最小方差无失真响应是经典的最大化阵增益的超指向性波束形成方法。圆环阵能够提供水平全向360°的均匀波束, 并且没有左右弦模糊。利用圆环阵型的对称性, 人们分别提出了相位模态域[4]、差分[5]和特征波束分解与综合[6-7](eigenbeam decomposition and synthesis, EBDS)等超指向性模型。圆环阵EBDS方法给出了超指向性的解析闭式解, 相比其他近似求解的超指向性模型更为精确, 在此基础上, 文献[8]给出了圆柱阵分两级子阵进行波束形成的EBDS超指向性数学模型, 与全局处理相比, 能够减少波束形成计算量, 但是此方法只能针对从水平方向入射的声信号。

文中提出针对圆柱阵任意俯仰角方向都能进行EBDS超指向性波束形成的数学模型。首先, 把圆柱阵上具有相同水平方位角的阵元(相当于一个垂直的线阵)作为第1级子阵, 在任意指定的俯仰角方向上进行常规波束形成, 这样圆柱阵就转换为一个带有指向性阵元的圆环阵; 将此圆环阵作为第2级子阵, 求解其在各向同性噪声场中噪声互谱矩阵, 由于此矩阵具有循环特性, 可以采用EBDS模型得到圆柱阵超指向性的最优解。文中将EBDS超指向性方法从单一水平方向推广到任意俯仰角方向, 拓展了EBDS方法的适用范围, 增强了圆柱阵的探测性能, 为进一步将小型圆柱阵成功应用于水下无人系统平台提供了参考。

1 高阶超指向性信号模型

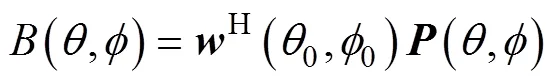
波束的指向性因子可表示为

在三维空间各向同性均匀噪声场中, 最大指向性因子的值等于最优阵增益, 由此得到最优加权值为[2]

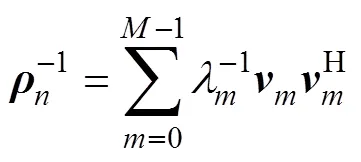
则基于特征波束分解与综合模型的最优加权向量可重写为[6]

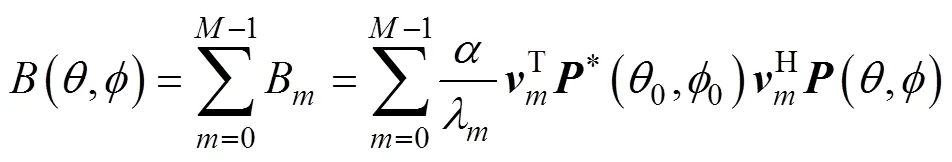
(12)

式中,为偶数。

2 圆柱阵子阵分级波束形成

2.1 两级子阵波束形成信号模型

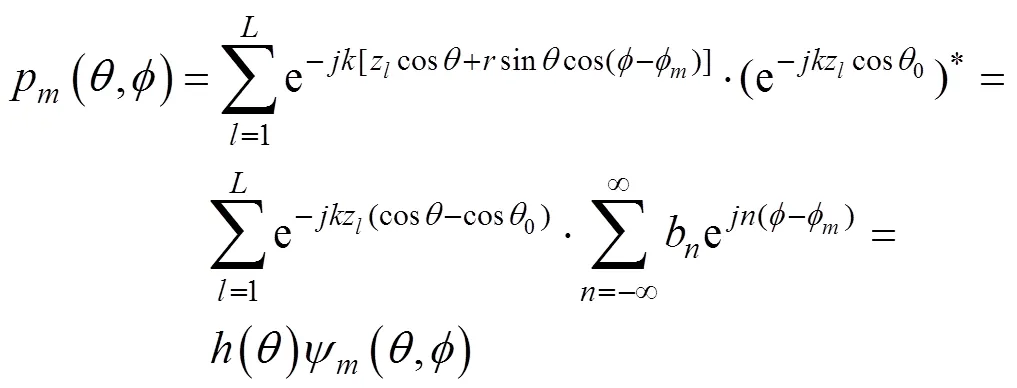
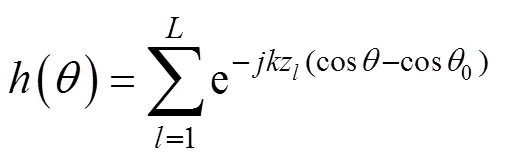
通过子阵第1级常规波束形成, 圆柱阵等效转化为圆环阵, 包含有个带有指向性的阵元。在此基础上可进一步求解其噪声互谱矩阵。

2.2 噪声互谱矩阵

3 仿真分析

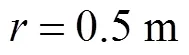
3.1 波束图

为进一步体现圆柱阵EBDS方法指向性的优势, 图5给出了CBF和EBDS方法的三维波束图, 可以看到, CBF方法在低频时几乎没有明显的指向性, 而EBDS方法指向性明显。由于EBDS超指向性波束具有宽带恒定束宽特性, 所以在一定低频范围内, EBDS方法能够保持恒定的较窄波束, 这也是超指向性方法的优势所在。当过小(频率过低)时, 超指向性方法的稳健性也会大大降低, 但是可以采用降秩技术提高稳健性, 截断不稳健的高阶项而保留稳健性较高的低阶项。

3.2 指向性因子和阵增益

图6给出了圆柱阵EBDS方法随变化的各阶特征波束的理论指向性因子。在值为0.4~4的范围内, 阶数越高, 指向性因子越大; 当值小于0.4时, 第5阶和第6阶指向性因子逐渐减小至0, 这是因为高阶特征波束对误差更敏感, 其特征值在较小时变得极小(小于10–16), 从而给计算带来了一定的误差。

图7是CBF和EBDS方法随变化的阵增益曲线。其中EBDS曲线是图6中各阶特征波束指向性因子相加求和的结果。从图7中可以看出, EBDS方法在低频段的阵增益远远高于CBF方法。在值小于0.4时, EBDS方法的阵增益有所减小, 这是因为在频率过低时, EBDS方法的高阶波束由于对误差的敏感性, 其指向性因子变小, 图6说明了这一问题。因此当> 0.4时, 各阶特征波束均处在稳健的范围内, 可选择全部阶数的指向性因子进行求和; 当0.2 << 0.4时, 第6阶特征波束已经不稳健, 此时可选择第1~5阶指向性因子进行求和; 当< 0.2时, 可根据特征波束的稳健性情况, 采用降秩技术适当舍弃不稳健的高阶指向性因子。

4 结束语

文中提出了圆柱阵在任意俯仰角方向进行EBDS超指向性波束形成的数学模型。首先, 把圆柱阵上具有相同水平方位角的阵元作为第1级子阵, 在任意指定的俯仰角方向上进行常规波束形成, 得到一个带有指向性阵元的圆环阵; 将此圆环阵作为第2级子阵, 求解了其在各向同性噪声场中噪声互谱矩阵, 然后采用EBDS模型得到圆柱阵超指向性的最优解。仿真结果表明, 文中提出的圆柱阵分2级子阵进行波束形成的超指向性波束形成方法在低频段的指向性和阵增益远高于常规波束形成, 将圆柱阵EBDS超指向性方法从单一水平方向推广到任意俯仰角方向, 拓展了EBDS方法的适用范围, 增强了圆柱阵的探测性能, 为进一步将小型圆柱阵成功应用于水下无人系统平台提供了理论参考。

[1] Stojanovic M. High-speed Underwater Acoustic Communications[M]. U.S.: Springer, 2002: 1-35.

[2] 汪勇, 杨益新, 马远良. 圆环形声学传感器阵列超指向性理论及方法[J]. 水下无人系统学报, 2017, 25(4): 297- 310.Wang Yong, Yang Yi-xin, Ma Yuan-liang. Discussion about the Superdirective Beamforming Theory and Methods of Circular Acoustic Sensor Arrays[J]. Journal of Unmanned Undersea Systems, 2017, 25(4): 297-310.

[3] Capon J. High-Resolution Frequency-Wavenumber Spectrum Analysis[J]Proceedings of the IEEE, 1969, 57(8): 1408-1418.

[4] Meyer J. Beamforming for a Circular Microphone Array Mounted on Spherically Shaped Objects[J]Journal of the Acoustical Society of America, 2001, 109(1): 185-193.

[5] Benesty J, Chen J. Study and Design of Differential Microphone Arrays[M]. Berlin: Springer-Verlag, 2013: 184.

[6] Ma Y L, Yang Y X, He Z Y, et al. Theoretical and Practical Solutions for High-order Superdirectivity of Circular

Sensor Arrays[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 203-209.

[7] Wang Y, Yang Y X, Ma Y L, et al. High-order Superdirectivity of Circular Sensor Arrays Mounted on Baffles[J]. Acta Acustica United with Acustica, 2016, 102(1): 80-93.

[8] 朱少豪, 汪勇, 杨益新. 圆柱阵子阵分级处理的稳健超指向性波束形成方法[J]. 声学学报, 2018, 43(4): 600-611. Zhu Shao-hao, Wang Yong, Yang Yi-xin. Robust Superdirective Beamforming for Cylindrical Arrays Based on Subarray Processing[J]. Acta Acustica, 2018, 43(4): 600-611.

[9] Trees V H L. Optimum Array Processing : Part IV of Detection, Estimation and Modulation Theory[M]. U.S.: Wiley-Interscience, 2002: 293-303.

[10] Tee G J. Eigenvectors of Compound-Circulant and Alternating Circulant Matrices[J]. Department of Mathematics the University of Auckland New Zealand, 2005, 36(6): 195-211.

[11] Bertilone D C, Killeen D S, Bao C. Array Gain for a Cylindrical Array with Baffle Scatter Effects[J]. Journal of the Acoustical Society of America, 2007, 122(5): 2679- 2685.

Superdirective Beamforming Method for Cylindrical Arrays Based on Eigenbeam Decomposition and Synthesis

ZHU Shao-hao, YANG Yi-xin, WANG Yong

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

To apply the small-aperture sensor array with relatively high spatial directivity to the space-limited unmanned undersea systems or other platforms, the superdirective beamforming method is used to improve thespatial directivity and array gains of the sensor array, and the target detection performance of the array is improved. First, a superdirective beamforming method based on eigenbeam decomposition and synthesis(EBDS) for circular arrays is introduced; then, a superdirective beamforming model for cylindrical arrays is proposed by using two-level subarrays at arbitrary pitch direction, and the noise cross-spectral matrix with circulant property in the isotropic noise field is derived. Simulation results of beampatterns and array gains show that the proposed superdirective beamforming method has many advantages over the conventional beamforming method in the directivity and the array gain at low frequency, which extends the application scope of cylindrical arrays with the EBDS and enhances the detection ability of cylindrical arrays. This study may provide a reference for application of small-aperture sensor array to detection of unmanned undersea systems at low frequency.

unmanned undersea system; superdirectivity; decomposition and synthesis(EBDS); cylindrical array

TJ630.34; TB566

A

2096-3920(2018)05-0421-06

10.11993/j.issn.2096-3920.2018.05.007

2018-08-30;

2018-09-19.

国家重点研发计划(2016YFC1400200); 国家自然科学基金项目(11604259); 装备预研领域基金项目(6140451020116HK03001).

朱少豪(1989-), 男, 在读博士, 主要研究方向为水声信号处理.

朱少豪, 杨益新, 汪勇. 圆柱阵特征波束分解与综合超指向性波束形成方法[J]. 水下无人系统学报, 2018, 26(5): 421-426.

(责任编辑: 许 妍)