分布式声学黑洞浮筏系统隔振性能研究

2022-07-14庞福振

振动与冲击 2022年13期

赵楠，王禹，陈林，庞福振

(1.驻上海地区第八军事代表室，上海 200011； 2.中国船舶及海洋工程设计研究院，上海 200011;3.哈尔滨工程大学船舶工程学院，哈尔滨 150001)

声学黑洞(acoustic black hole，ABH)是近年来新兴的减振降噪技术，其结构特点为厚度h与距离尖端的距离x符合h(x)=εxm(m≥2)的函数关系，其功能特点为弯曲波在结构尖端聚集，波长逐渐减小并趋近于0，发生尖端无反射现象[1-2]，从而降低弯曲波在结构中的传递，实现减振降噪的目的。

目前，已有大量学者对声学黑洞结构做出相关研究[3-6]；何璞等[7]基于一维声学黑洞原理，提出声学黑洞盒式结构，并利用有限元分析方法探究了该结构的振动特性，研究表明声学黑洞盒式结构对振动峰值具有5～30 dB的削减作用；郭浩[8]提出一维声学黑洞杆结构，并将该结构应用于球拍设计和动力吸振器设计，研究表明，带有阻尼的声学黑洞结构能够有效降低振动响应峰值；刘尊程等探究了二维声学黑洞薄板的振动特性，并将其应用于浮筏结构上，研究表明内嵌二维声学黑洞的浮筏结构可有效提升其隔振性能；李熙等[9-11]则从理论和试验角度对声学黑洞结构减振效果进行对比研究，研究表明，声学黑洞结构减振效果良好，其结构参数对减振效果影响较大。

综上可以看出，声学黑洞具有结构简单，抑振效果良好等特点，但在船舶浮筏系统中应用声学黑洞过程中，由于浮筏结构形式限制，可嵌入声学黑洞的区域较少，其对浮筏隔振性能的提升有限；为此，本文结合工程实际问题，提出分布式声学黑洞应用方案，采用四个小尺寸声学黑洞代替单个大尺寸声学黑洞，利用数值仿真方法，依次探究了分布式声学黑洞对平板结构、典型筏架结构以及浮筏隔振系统的抑振效果，最终以某船舱段为研究对象，采用分布式声学黑洞方案，降低了船舶机械噪声水平，能够在有限区域内进一步提升声学黑洞的抑振性能，为船舶减振降噪提供新的思路和参考。

1 声学黑洞基本原理

声学黑洞结构是基于天文学中黑洞概念提出的，声学黑洞结构在厚度上满足特定的幂律关系：h(x)=εxm(m≥2)，理想情况下，声学黑洞结构具备弯曲波尖端无反射的特性，向结构尖端传递的弯曲波将被困在尖端，同时振动的能量也将在尖端汇聚并耗散。

一维声学黑洞基本结构形式如图1所示。

图1 一维声学黑洞结构示意图Fig.1 Schematic diagram of one-dimensional ABH

根据文献[1]中对声学黑洞基本原理的描述可知：当弯曲波向声学黑洞尖端边界传播时，结构上任一点到结构尖端整体波的相位为

(1)

式中，k(x)为弯曲波在结构上的局部波束。其具体指为

(2)

可以看出在特定频率下，kp为一常数，在m大于等于2的条件下，当x趋于0则有k(x)趋于无穷，说明在结构尖端位置，局部波数趋于无穷，波长趋于0。即弯曲波永远无法到达结构尖端位置，也将无法发生反射现象。实现声学黑洞结构的减振效果。

将一维声学黑洞截面，绕其尖端旋转一周，形成中心凹陷的圆盘结构即为二维声学黑洞，其基本结构形式如图2所示。

图2 二维声学黑洞结构示意图Fig.2 Schematic diagram of two-dimensional ABH

弯曲波在二维声学黑洞中传播过程中，会在厚度变化区域发生偏转，将汇集在声学黑洞中心位置并耗散，实现对结构振动响应的抑制[12]。

但工程实际中，由于尖端厚度趋于0，使得结构加工较为困难，无法达到理论上对弯曲波的完全吸收，一般情况下，将对其尖端结构进行截断，并附加一定的阻尼材料，以弥补尖端阶段对声学黑洞结构噪声的负面影响。

2 分布式声学黑洞浮筏系统设计

2.1 分布式声学黑洞方案设计

本文采用四个声学黑洞替代单个大尺寸声学黑洞，形成分布式声学黑洞应用方案，其中分布式声学黑洞的半径为单个声学黑洞半径的一半，保证两种方案中声学黑洞的面积相同。分布式声学黑洞示意图如图3所示。

四个声学黑洞的方案可以在保持声学黑洞总面积恒定的条件下，不明显改变声学黑洞占用结构的区域。两个或者三个声学黑洞的方案则不具备上述的优势。在分布式声学黑洞方案中，声学黑洞的位置以尽可能减小对原结构的改变为原则，均匀紧凑的分布在结构中。

为验证分布式声学黑洞方案的有效性，本章依次以平板结构、典型筏架结构为研究对象，开展分布式声学黑洞对结构振动响应的抑制效果研究，并与单个声学黑洞方案的抑振效果进行对比分析。

2.2 分布式声学黑洞方案对结构抑振效果分析

2.2.1 分布式声学黑洞平板结构振动特性分析

(1) 声学黑洞平板模型

为验证分布式声学黑洞方案的有效性，对比单个声学黑洞与分布式声学黑洞方案对平板结构振动响应的抑制效果的差异，建立如图4所示的声学黑洞平板模型，主尺度为长360 mm，宽250 mm，厚6 mm，声学黑洞区域黑洞结构半径为100 mm，模型激励点为水平中线距离右端50 mm位置处的P0点，激励力载荷为单位力，振动响应考核点为P1～P8，其中，用点P1～P5的平均振动加速度级表示结构边缘的振动水平，用点P6～P8的平均振动加速度级表示激励点附近区域的振动水平，如图4所示。

图4(a)中声学黑洞半径为100 mm，厚度变化符合函数h(r)=6/10 000×r2，r为与声学黑洞中心的距离，去除声学黑洞结构中r<10 mm区域内的结构，并用恒定厚度板填充该区域，使得结构整体厚度变化连续，在声学黑洞中心位置附加半径为20 mm，厚度为2 mm的阻尼材料。图4(b)为分布式声学黑洞平板，嵌入四个小尺寸声学黑洞，每个声学黑洞半径为25 mm，去除声学黑洞结构中r<2.5 mm区域内的结构，阻尼材料半径为5 mm。

在进行有限元建模分析时，采用具有不同厚度属性的板单元来对声学黑洞的变厚度区域进行建模，该方法解决声学黑洞厚度连续变化带来的网格划分困难问题[13]，提高了计算效率，并且与实体单元模型的振动响应吻合良好。

(2) 声学黑洞平板振动特性分析

采用有限元法对上述声学黑洞平板进行相应分析，所建立的有限元计算模型如图5所示，其中声学黑洞区域被划分为45个具有相同宽度的同心圆环，每个圆环具有不同的厚度属性。

所得考核点平均振动响应曲线如图6和7所示。

图6 考核点P1～P5平均振动响应Fig.6 Average vibration response of points P1-P5

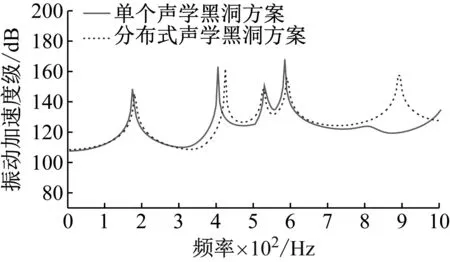
图7 考核点P6～P8平均振动响应Fig.7 Average vibration response of points P6-P8

从图6和7可以看出：分布式声学黑洞平板的振动响应曲线在900 Hz产生了一个新的峰值，是由于分布式声学黑洞嵌入后产生的新的振动模态所导致，但该处峰值大小较小；在前几个峰值位置处，分布式声学黑洞平板振动响应峰值均向高频方向发生偏移，峰值大小约下降3～7 dB。说明四个声学黑洞的设计将提高对低频弯曲波的捕获能力，降低声学黑洞平板在低频范围内振动响应。

2.2.2 分布式声学黑洞典型筏架结构振动特性分析

通过前文的研究可知，分布式声学黑洞对平板的抑振效果更好，但筏架结构本身是相对复杂的三维立体结构，为此本节以典型筏架结构为研究对象，典型筏架结构具有筏架的基本特征结构，进一步探究分布式声学黑洞方案对典型筏架结构的振动特性。

(1) 声学黑洞典型筏架结构模型

筏架典型支撑结构如图8所示的，其中上下面板长680 mm，宽580 mm，厚度为11 mm，垂向支撑板厚度为12 mm，上层隔振器连接板面板厚度为18 mm，下层面板隔振器连接板面板厚度为11 mm；筏架整体高度400 mm。

将几何模型进行离散，保证每个波长中有6个网格，所得有限元模型如图9所示。其中声学黑洞嵌入位置为下层隔振器垂向支撑板中心，图9(b)为单个声学黑洞典型筏架，声学黑洞半径为96 mm，厚度变化符合函数h(r)=6/962×r2，r为与声学黑洞中心的距离，去除声学黑洞结构中r<9.6 mm区域内的结构，并用恒定厚度板填充该区域，使得结构整体厚度变化连续，在声学黑洞中心位置附加半径为19.2 mm，厚度为2 mm的阻尼材料，图9(c)为分布式声学黑洞典型筏架，声学黑洞尺寸均为图9(b)中声学黑洞尺寸的一半。

(2) 声学黑洞典型筏架结构振动特性分析

考虑到隔振器下表面通常采用四角螺栓连接方式，因此激励点位置为上层隔振器面板共设有四个激振力，大小为单位力，考核点位置为下层隔振器面板的均方振速。经计算，得到1 000 Hz频率范围内不同计算模型的振动响应曲线如图10所示。

图10 声学黑洞典型筏架结构考核点振动响应曲线Fig.10 Vibration response curve of typical raft structure check point of ABH

从图10中可以看出：

(1) 单个声学黑洞或分布式声学黑洞典型筏架结构能有效降低考核点在1 000 Hz以内的大部峰值的振动响应大小。

(2) 相比于无声学黑洞典型筏架结构，分布式声学黑洞典型筏架结构考核点的振动响应控制较好，大部分频点减振效果可达3～9 dB，部分频点减振效果更佳可达20 dB以上；

(3) 相比于单个声学黑洞典型筏架，分布式声学黑洞典型筏架响应曲线中大部分峰值减振效果提升1 dB以上，最多可提升3.8 dB。

综上可以看出，分布式声学黑洞方案能够在不明显改变结构的条件下，更好的对典型筏架结构的振动响应进行控制，提高了典型筏架结构的隔振性能。

2.3 分布式声学黑洞浮筏系统模型

由前文可知分布式声学黑洞方案可进一步提高典型筏架结构的隔振效果，本节将以某船舶大型浮筏隔振系统为基础，设计分布式声学黑洞浮筏系统。

在浮筏系统建模时，采用刚体对所承载的设备进行建模，其质量为2.1 t；采用4节点shell单元进行筏架结构和基座结构建模，筏架主尺度为模型总尺寸为3 500 mm×2 000 mm×400 mm；采用弹簧阻尼系统进行隔振器单元建模，上层隔振器12个，下层隔振器6个，隔振器参数如表1所示，最终浮筏隔振系统有限元分析模型如图11所示。

表1 隔振器参数Tab.1 Vibration isolator parameters

浮筏结构形式复杂，在确定声学黑洞嵌入位置时，考虑到筏架结构受到激振力位置为上层隔振器的面板处，激振力产生的弯曲波将依次由面板传递至肘板、支撑板以及整个筏架结构，为了更好的对弯曲波进行吸收和耗散，本次声学黑洞嵌入位置为筏架上层隔振器连接板肋板位置处，该位置距离激振点较近，是弯曲波传播的主要路径，此外，肘板结构应力分布呈现指端应力大，中心应力的小的规律，声学黑洞的嵌入对原结构相对较小，结构依然连续完整，结构强度不是主要问题，本文暂不做讨论。在分布式声学黑洞方案中，为了使得声学黑洞更均匀的嵌入在肘板结构中，采用三角形的排布形式，具体声学黑洞嵌入方案及有限元模型如图12所示。