双浮动密封橡胶O形圈接触应力分析*

2022-07-14王永乐沈宗沼丁思云

润滑与密封 2022年7期

王永乐谢星李香沈宗沼丁思云

(合肥通用机械研究院有限公司安徽合肥 230031)

工程机械设备、煤矿机械设备等长期工作在含泥沙颗粒等恶劣环境下，其旋转动密封是十分关键的部件，直接影响着设备的可靠性和工作效率。目前采用较多的橡塑或聚氨酯材料唇形密封，在运转过程中存在润滑脂损耗严重、磨损失效和寿命短等问题。双浮动端面密封由于其特殊的结构，可适用于泥沙等恶劣工况条件，且具有结构简单、耐磨损、耐振动冲击、密封性好以及寿命长等优点[1]，目前已逐渐应用于掘进机滚刀、推土机履带负重轮两端及采煤机滚筒和减速器等工程机械密封系统[2-4]。

一般双浮动密封是由一对端面硬度很高的金属浮动动环、静环及对应安装的橡胶O形圈和浮封座构成，其结构对称，通过O形圈轴向压力压紧形成端面密封。双浮动密封装置结构如图1所示。其中，O形圈作为密封环的弹性补偿元件，被摩擦力固定在浮封座内；同时其还具有辅助密封功能，这对双浮动密封的运行起着非常关键的作用。许多学者对橡胶O形圈的受力进行了分析计算及试验研究。李振涛等[5]利用ABAQUS软件建立O形圈轴对称模型，对不同工况下O形圈的应力分布规律进行分析，确定了O形密封圈材料易失效的位置。刘杰夫和吕晓仁[6]分析了盾构机密封O形圈静态接触下应力与压缩率、流体压力、硬度等的变化规律，但未能模拟真实结构参数，即不同斜面角度下的接触模型。蔡智媛等[7-8]利用有限元软件分析了轴安装过程中O形圈的应力变化及对静密封性能影响规律。SUKUMAR等[9]对不同硬度值的O形圈试样进行了应力-应变数据测量，并作为有限元参数进行分析计算。SANG等[10]利用有限元软件分析了液压密封O形圈的轴向摩擦力、最大摩擦应力及接触应力，并通过试验测试验证了数值计算的有效性。

图1 双浮动密封结构示意

目前的研究针对O形圈平面压缩较多，对具有一定倾斜角的接触问题研究很少见。本文作者以双浮动密封为研究对象，利用有限元方法开展不同浮封座和浮动环的斜面角度等对O形圈接触过程应力影响的研究，为双浮动密封结构设计提供理论指导。

1 计算模型

1.1 几何模型

依据JB/T 8293—2014《浮动油封》标准的规定，选取公称尺寸为220 mm×187 mm×19 mm的浮动环和浮封座作为研究对象进行分析，对应橡胶O形圈尺寸为φ200 mm×11.5 mm,浮封座斜面角度α=10°。O形圈初始位置分别与浮封座及浮动环相切。由于双浮动密封结构的对称性，文中将其简化为二维轴对称模型并取其一侧进行分析。简化后的几何模型如图2所示。

1.2 有限元模型

双浮动密封结构参数、压缩状态等因素对O形圈的受力和密封性能起着关键作用。O形圈的应力分析计算属于几何非线性、材料非线性和状态非线性的接触问题，文中采用增广拉格朗日接触算法处理。其特点是：接触压力对于接触刚度的敏感性降低，有利于在给定接触刚度较大时计算收敛，也可以一定程度上提高计算精度。橡胶材料属于超弹性近似不可压缩体，其本构关系是复杂的非线性函数，通常用应变能函数表示。目前广泛采用Mooney-Rivlin模型描述橡胶材料的应变能函数，同时附加体积约束能量项，得到修正的应变能函数[11]。文中采用双参数的Mooney-Rivlin模型进行计算，其本构方程为

W=C10(I1-3)+C01(I2-3)

式中：I1、I2为应变张量的2个主不变量；C10和C01为材料常数。

根据相关标准[12]的推荐及工程应用经验，文中选用邵氏A70度的丁腈橡胶为O形圈材料，其对应材料参数为：C10=0.739 MPa，C01=0.185 MPa[13]。

由于浮动环及浮封座的刚度远大于橡胶材料，文中不考虑其变形，故将其设置为刚体。由于密封两侧压差非常小，所以不考虑介质压力的影响。为模拟安装过程，将浮封座整体轴向压缩率设置为S，浮动环端面设置为固定约束。将O形圈与浮动环背斜面及浮封座内斜面分别定义为2个接触对，接触类型设置为摩擦。橡胶与金属件的摩擦因数初步设置为0.2[14]。进行网格划分时，对O形圈进行了加密处理，将其单元尺寸设为0.4 mm。

2 计算结果及分析

2.1 压缩率对O形圈应力的影响

图3示出了O形圈在压缩率S为4%～24%(轴向压缩距离分别为2～12 mm)时的von Mises应力分布。可以发现：起初O形圈的最大应力分别出现在与2个刚体接触位置附近；随着压缩率的增加，接触带宽度随之增加，高应力区域不断扩大并逐渐连通形成哑铃型；随着压缩率的进一步增加，高应力区域逐渐缩小到中部形成椭圆形，并向外发散减小；压缩过程中O形圈所受等效应力分布较均匀。但当压缩率S=24%时，由于O形圈上部与浮动环接触并发生挤压变形，导致最大应力位置发生变化，右侧分布偏多。

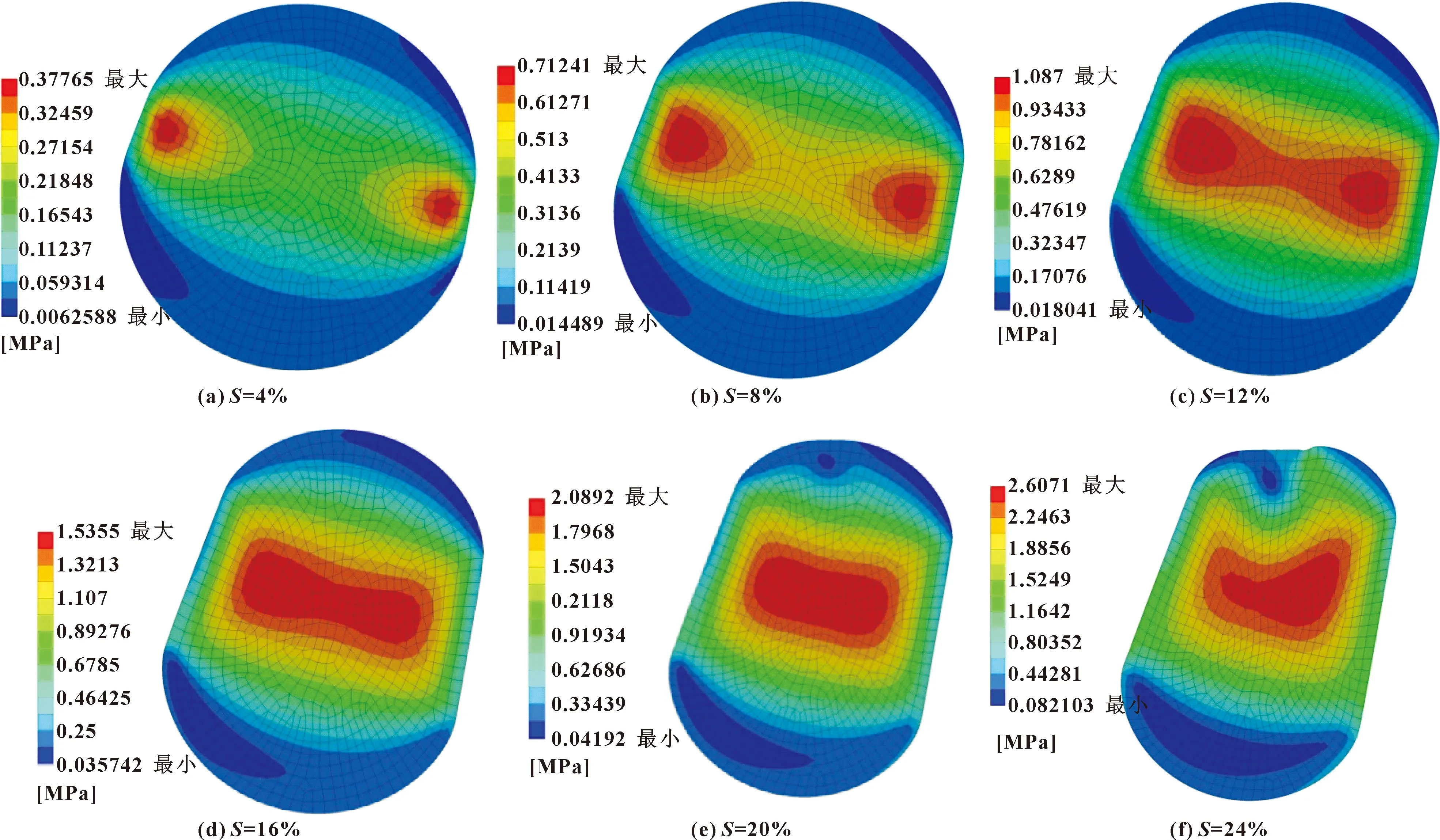
图3 不同压缩率S下的von Mises应力分布

图4所示为O形圈在轴向压缩率S为4%～24%时平面剪切应力分布。可以看出，随着压缩率的增加，最大剪切应力范围由两侧开始的接触位置附近向中间扩大，压缩过程中高剪切应力始终处于有相对转动的接触部位前端位置。当S=24%时，由于O形圈上部与浮动环接触，导致最大剪切应力位置发生变化，如图4(f)所示，最大剪切应力位置主要集中分布于右侧上部接触位置附近。由于橡胶圈抗剪切变形能力远小于其抗压缩变形能力，所以最大剪切应力位置也反映了O形圈易出现损坏的部位。在设计中，应在满足密封性能的前提下，尽量减小O形圈所受的最大剪切应力。

图5示出了S=20%时O形圈整体位移情况。由于在整个压缩过程中，两侧刚体对O形圈接触部位产生摩擦、挤压作用，使O形圈相对产生逆时针的转动，最大位移出现在其右侧与轴向移动的浮封座接触位置的前端。接触压力反映的是O形圈与刚体接触对间的压力，其最大值反映了O形圈密封力的大小。当接触压力小于密封流体压力时，接触对间可能出现缝隙，导致泄漏量增大，使密封失效。图6所示为压缩率S=20%时对应的接触压力分布。可以发现：最大接触压力分别位于两侧接触部分中心位置，并向外逐渐减小。此时，有利于油膜进入外部密封间隙，对密封起到一定的润滑及散热作用，最大密封力达2.4 MPa。

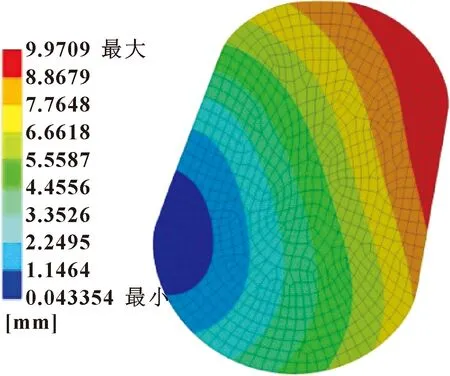
图5 总变形(S=20%)

图6 接触压力分布(S=20%)

图7示出了各应力最大值随压缩率的变化。可知，最大等效应力与接触压力随压缩率的增大增幅相对较大，且二者的增长率相近，这说明压缩率的增加能明显提高O形圈的密封力。最大剪切应力也几乎呈线性增加，但变化幅度相对较小。当S>20%时，剪切应力增幅明显变大，此时不利于O形圈的受力。所以，在满足密封力及端面比压的前提下，要保持适当的压缩率才能提高O形圈的使用寿命。而过大的压缩率会使橡胶圈产生永久性变形、降低其弹性、加剧老化，进而引起密封失效。

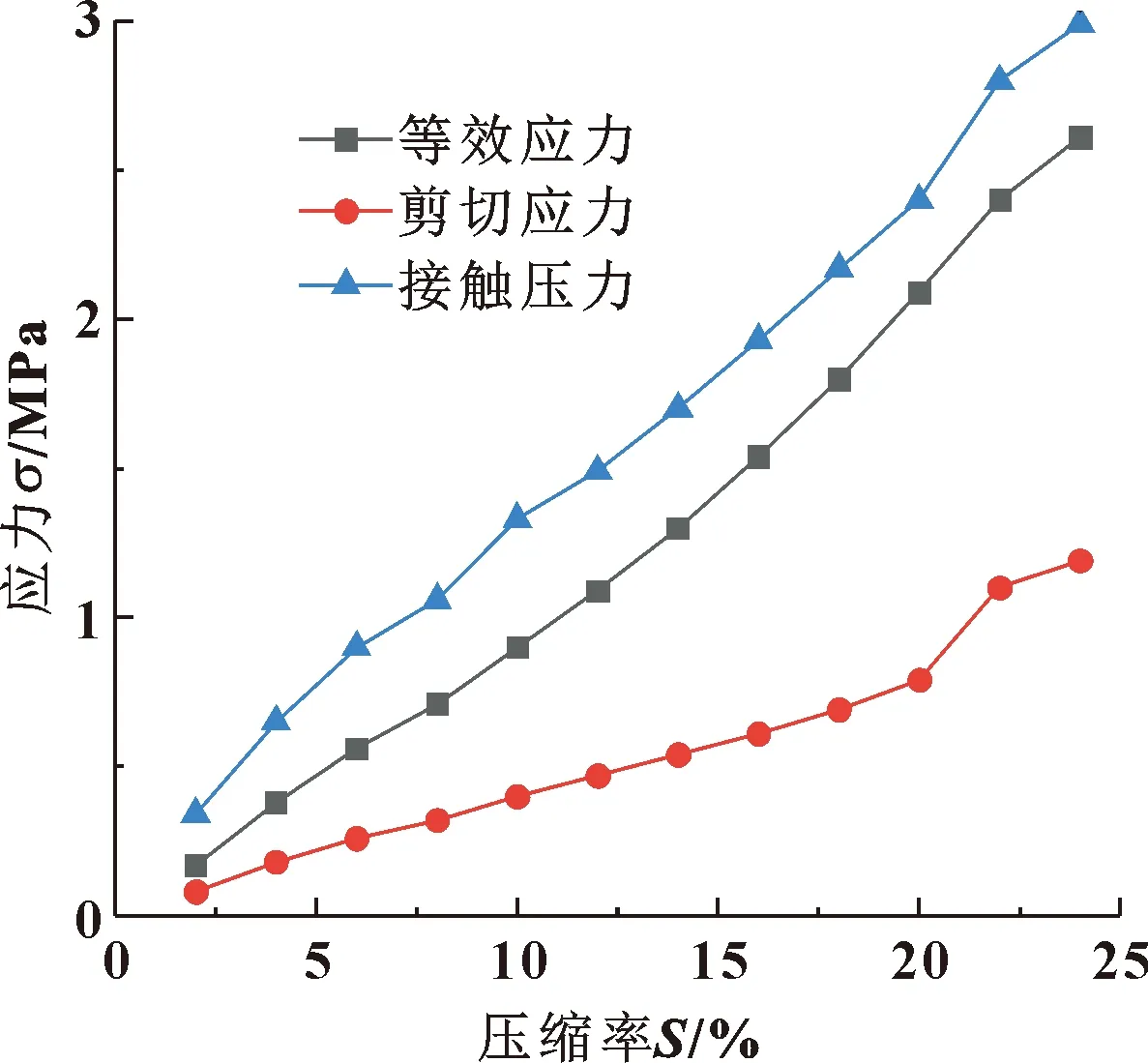
图7 各应力最大值随压缩率的变化

对压缩过程中O形圈与浮封环接触位置的网格节点按逆时针顺序从0～25进行编号，图8所示为O形圈在不同的压缩率下，左侧接触对不同节点编号上的接触压力。可见，接触压力均呈现抛物线形分布，最大接触压力位于接触部位的中心处，其幅值随着压缩率S的增大而增大；随着压缩率S的增大，接触部位发生了移动，接触压力范围及数值也随之增大。

2.2 结构参数对O形圈应力的影响

在浮动密封结构中，浮封座斜面角度α、浮动环斜面角度β是2个重要的结构参数，其角度的变化直接影响O形圈的受力。如图9所示，在β=21°时，随着浮封座斜面角α的增加，等效应力总体趋于减小，接触压力先减小后缓慢增加，而剪切应力整体变化较小，并在α=10°时处于最小。如图10所示，在α=10°时，随着浮动环斜面角β的增加，等效应力、接触压力呈递增趋势，但剪切应力上下波动，整体变化不明显，在β=21°时，剪切应力最小。

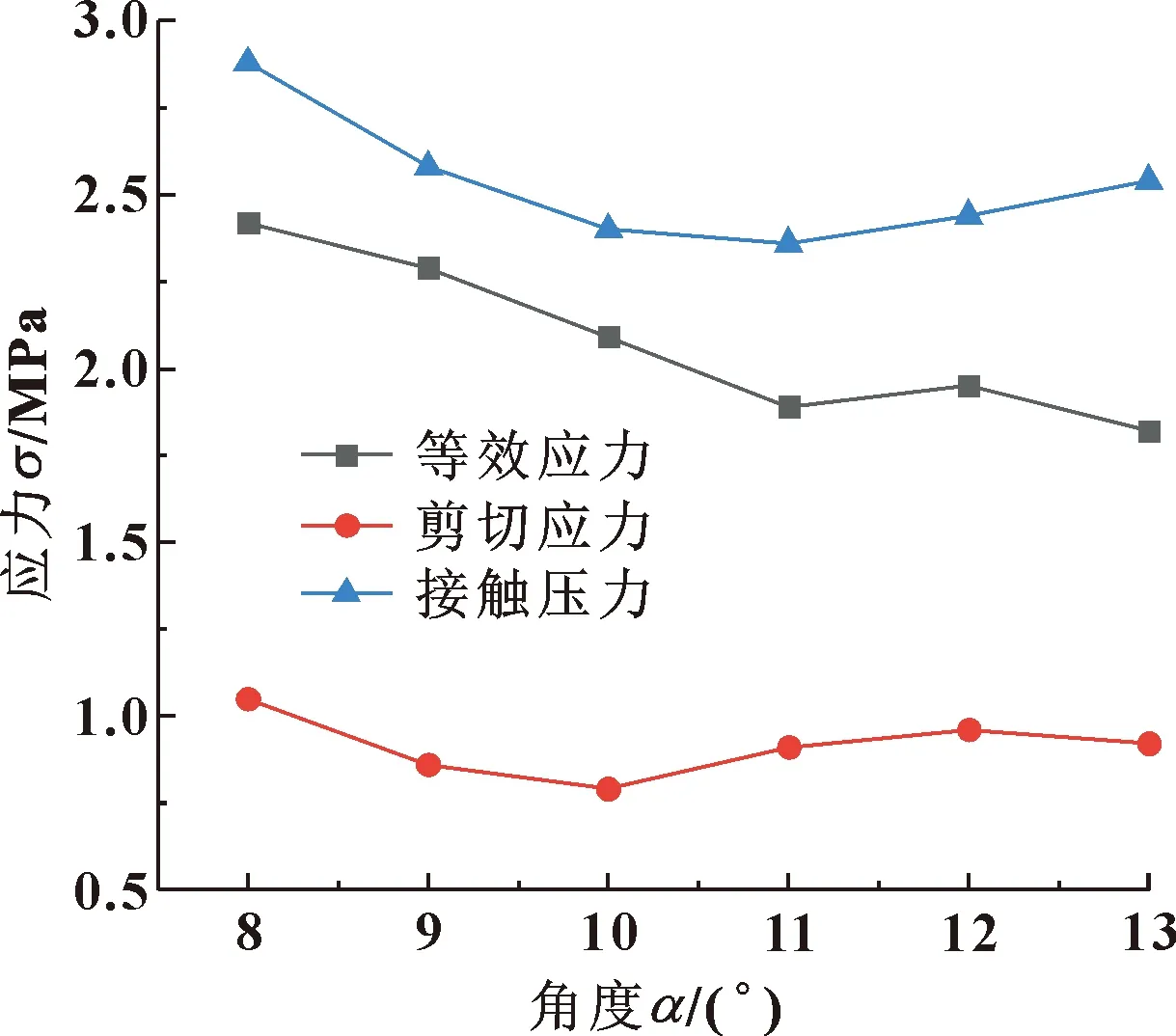
图9 浮封座斜面角度α对应力的影响(β=21°)

最大剪切应力最小时，O形圈最不易发生剪切失效[6]。所以，当α=10°、β=21°时，在保证密封性能的同时，有利于O形圈的受力。

图10 浮动环斜面角度β对应力的影响(α=10°)

2.3 摩擦因数对O形圈应力的影响

为保证橡胶O形圈能够传递足够的扭矩而不打滑，浮动环的背斜面与浮封座的内斜面需具有一定的表面粗糙度，一般推荐值为Ra6.3～12.5 μm[15]。图11示出了浮动环的背斜面与O形圈间的摩擦因数对O形圈应力的影响。可以发现：当O形圈与接触斜面的摩擦因数取0.1～0.4时，对于O形圈应力的影响很小，可以忽略不计，所以在进行密封设计时并非粗糙度值越大越好。