动态车辆共乘问题的双模式协作匹配算法
2022-07-12郭羽含刘永武
郭羽含 刘永武
(辽宁工程技术大学软件学院 辽宁葫芦岛 125105)
车辆共乘(ride-sharing)问题指对一定时空范围内的可用服务车辆与无车乘客的出行需求进行匹配并对其行驶路径进行规划,以提升运输资源利用率、减少车辆的并发使用,对降低运输成本、缓解交通拥堵、降低环境污染具有重要作用.
根据车辆提供的服务特性,一般将车辆共乘问题分为顺风车模式和出租车模式.其中,顺风车模式指车主和乘客通过共乘服务平台发布其各自行程,需最大化车主与乘客的共享路程;而出租车模式指车主以运输乘客赚取利润为目,需最小化车主所在地和乘客所在地间的无共乘路程[1].与顺风车模式相比,出租车模式仅移除了车主从乘客目的地行驶到自身目的地的过程,因此可看作顺风车模式的一种特例,故本文针对顺风车模式进行研究.
基于匹配实时性可将共乘问题分为静态共乘问题(static ride-sharing)和动态共乘问题(dynamic ride-sharing).静态共乘问题仅考虑一个固定时间窗口内的车主与乘客匹配及路径规划,且车主与乘客的出发时间和位置均可预先获取,匹配完成后车主根据规划的路径行驶,沿途不再进行后续匹配活动,路径也不再变更.此种共乘模式限制了车主的实载率,导致运输资源利用率降低、乘客的匹配等待时间增加.动态共乘问题考虑一个动态持续的过程,车主在行驶过程中可继续匹配沿途满足路程约束和乘客要求的待匹配乘客并持续优化车主的行驶路径.该模式对静态共乘进行了扩展,可更好地利用运输资源,降低乘客的等待时间.
相较于传统车辆路径规划问题[2-3]和静态共乘问题[4],国内外对于动态共乘问题的研究较少,文献[5-6]对本问题进行了综述,将其研究方向主要归纳为提高车主和乘客的匹配度[7-11]、降低行程开销[12-15]和减少用户等待时间[16-18]等方面.
1) 在提高匹配度方面.Zhang等人[7]设计了一种能够最大化乘客流动性的贪婪算法;Stiglic等人[8]以接客点来提高匹配方案的效率和灵活性;Zhan等人[9]建立了一个最大化服务乘客数量、最小化出行成本的动态共乘系统;Enzi等人[10]引入多模式汽车和乘车共享问题,并通过基于列生成的双层分解算法进行求解;Ta等人[11]设计了一种基于共享路程比率最大化的匹配模型.
2) 在降低行程开销方面.刘文彬等人[12]设计了一种以最小化车辆绕行距离为优化目标的线性时间插入操作方法;Alisoltani等人[13]使用基于动态出行的宏观模拟来评估解决方案,考虑了通过出行时间获得最优解决方案的拥堵效应和动态出行方案;Özkan[14]通过制定乘客共享模型证明了联合定价和匹配决策对系统性能有显著影响;Schilde等人[15]提出了2套考虑车辆行驶速度影响因素的元启发式匹配方案.
3) 在减少用户等待时间方面.Cheikh-Graiet等人[16]提出了基于禁忌搜索的元启发式动态拼车优化算法;曹斌等人[17]提出了一种高效的大规模多对多拼车匹配算法;肖强等人[18]基于泊松分布模拟了出租车合乘概率及等待时间.
由于动态共乘需实时计算数以万计的车主与乘客的匹配订单,因此对算法的求解效率和求解质量要求极高.虽然近年来已对动态共乘进行了部分研究工作,但在全局最优性、动态匹配实时性和共乘比率等方面仍存在不足.如文献[1,11]中提出的自适应搜索策略和近似解算法在考虑求解效率时并未考虑车主和乘客的匹配率;动态共乘问题对实时性要求较高,文献[19-25]在考虑车主匹配率或总体消耗时并未考虑车主的实时性匹配问题;文献[20-21,23-33]在优化总体行驶距离或总体行时间时忽略了车主和乘客间路径重合度,降低了车主和乘客的共乘路径,无法高效提高运输效率.表1对现有的代表性研究进行了总结,并分析了各研究对时间窗、绕行距离、总花费、匹配率等主要指标的考虑情况.
本文针对固定时空范围内的动态共乘问题展开研究,将匹配过程分为离线匹配阶段和在线匹配阶段.首先,提出通用共乘比率和首尾距离度2种评估标准,以准确地评估不同阶段的匹配价值;其次,提出一种基于约束时间窗和绕行距离约束的距离矩阵生成算法,于匹配前对车主和乘客集合进行筛选,从而降低数据规模,并通过改进的距离矩阵生成算法计算车主与乘客间的距离矩阵;再次,在离线匹配阶段提出一种基于带权路径搜索树的通用共乘比率生成算法以提升求解质量,从而提高全局匹配率;最后,于在线匹配阶段提出一种首尾距离度的实时订单插入算法,根据实时匹配到的乘客对离线匹配阶段生成的标准路径进行动态更新,在保证实时性的情况下进一步提升全局匹配率.
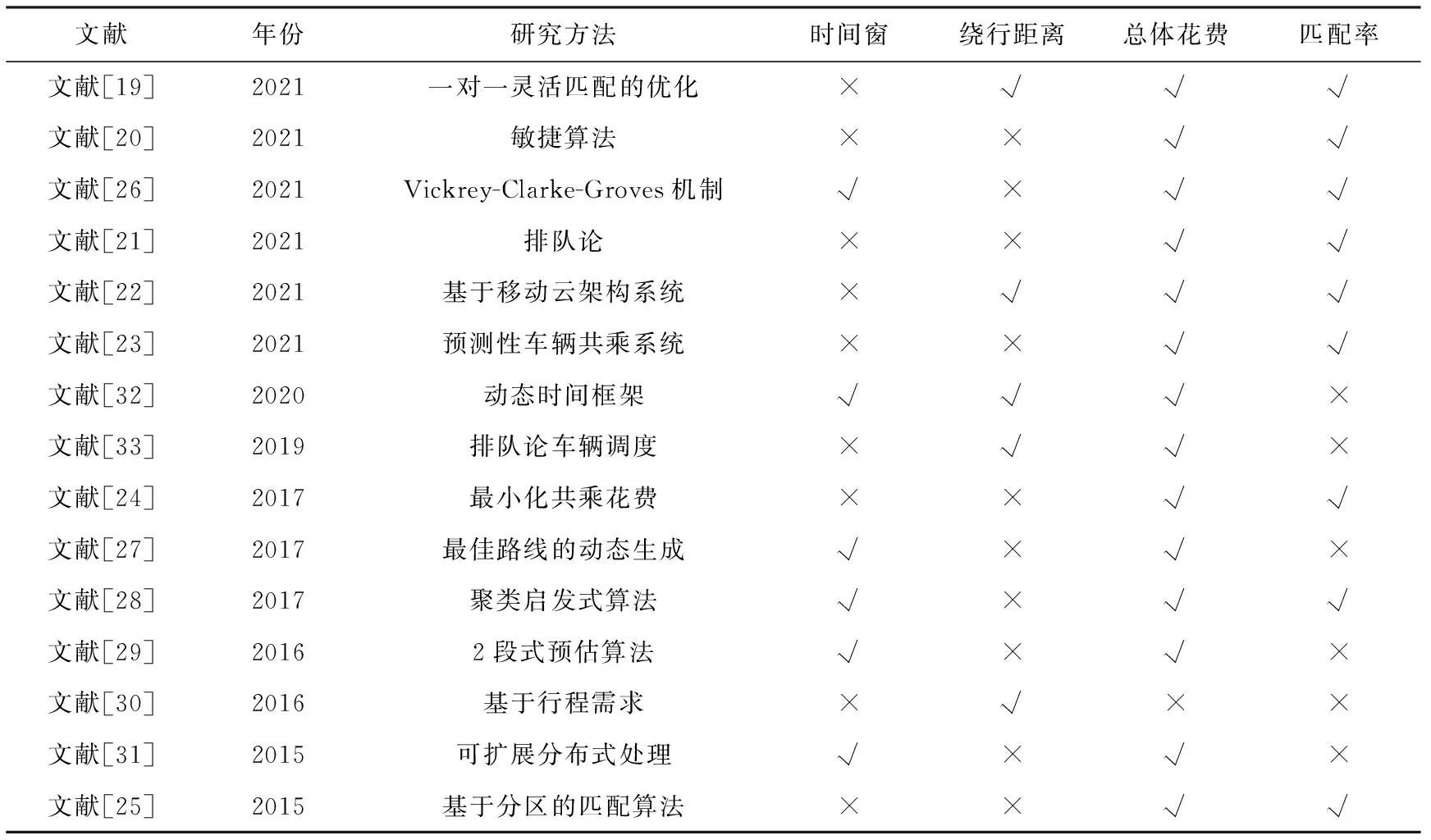
Table 1 Related Research Situation of Dynamic Ride-Sharing表1 动态共乘相关研究情况
本文的主要贡献有4个方面:
1) 针对动态共乘问题形式化定义了2种匹配价值评估标准,并建立了一种基于双模式协作匹配的数学模型,将匹配过程动态描述为离线匹配阶段和在线匹配阶段;
2) 于离线匹配阶段提出了带权路径搜索树中的单条带权路径理论,并基于此理论构建了一种基于带权路径搜索树的通用共乘比率生成算法;
3) 于在线匹配阶段提出了单一首尾距离度评估标准和基于2种距离系数的复合首尾距离度评估标准,结合实时更新标准路径的订单插入算法,构建了一种基于首尾距离度的实时订单插入算法;
4) 通过大量真实算例进行了实验分析,验证了本算法解决动态共乘问题的有效性,并证明了基于双模式的匹配方法可以大幅增加高价值共乘路程、降低车辆空载率,从而提升交通资源利用率.
1 问题建模
本节首先对动态共乘问题涉及的角色进行定义,然后对离线匹配阶段和在线匹配阶段及其优化目标进行建模.
1.1 角色定义
定义1.车主.集合D={di,i∈[1,m]∩}表示车主集,其中di代表车主i,车主当前状态statusi=[ldi,adi,Cdi,Tdi,Ldi]表示每个车主具有所在地ldi、目的地adi、车容量Cdi、出发时间Tdi和初始行驶路径Ldi五个属性.
定义2.乘客.集合R={rj,j∈[1,n]∩}表示乘客集,其中rj代表乘客j,以乘客行程tripsj=[lrj,arj,Trj]表示每个乘客具有所在地lrj、目的地arj和出发时间Trj三个属性.
在动态共乘匹配过程中,由于车主di能够沿途匹配多个乘客r,即单车主多乘客问题,传统共乘比率(shared route percentage,SRP)[34]只能处理单车主单乘客问题,在处理单车主多乘客时会变得异常复杂,因而求解匹配结果也变得尤为困难.本文基于带权路径搜索树提出了通用共乘比率,可在计算动态匹配问题时高效地求得匹配结果.传统共乘比率计算方式为
(1)
其中,dis(lrj,arj)表示乘客rj的所在地lrj和目的地arj间的距离;dis(ldi,lrj)表示车主di的所在地ldi与乘客rj的所在地lrj间的距离;dis(arj,adi)表示乘客rj的目的地arj与车主di的目的地adi间的距离.
定义3.通用共乘比率(general shared route per-centage,GSRP).GSRP是指车主与乘客共乘路径占车主因接送乘客行驶的总路径的比率.
对于任意车主di,给定一个带权路径搜索树Tree=(V,E)和权重函数ω:E→.其中,V表示为车主di的所在地和目的地与待匹配乘客rj的所在地和目的地组成的节点集,E表示节点间的边集;权重函数将2个节点间的每条边映射到实数值的权重上.搜索树中的单条带权路径swp=〈v1,v2,…,v2(c+1)〉的权重ω(swp)是构成该路径的所有边的权重之和:
(2)
对于任意的i和j,1≤i≤j≤2(c+1),其中c为当前匹配乘客数,定义从节点vi到节点vj的最短路径权重为
(3)
δ(v1,v2(c+1))即为单条带权路径的最短路径.λ为此最短路径中的共乘路径:
λ=swp-〈v1,v2〉-〈v2c+1,v2(c+1)〉.
(4)
通用共乘比率可表达为
(5)
则GSRP的形式可分解为共乘路径和单条带权最短路径2段路径:
(6)
s.t.i,j∈[1,2(c+1)],
(7)
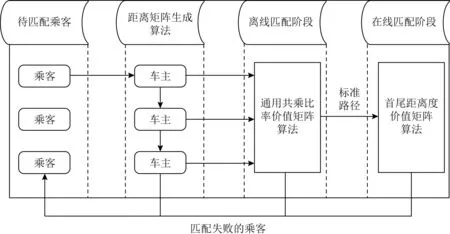
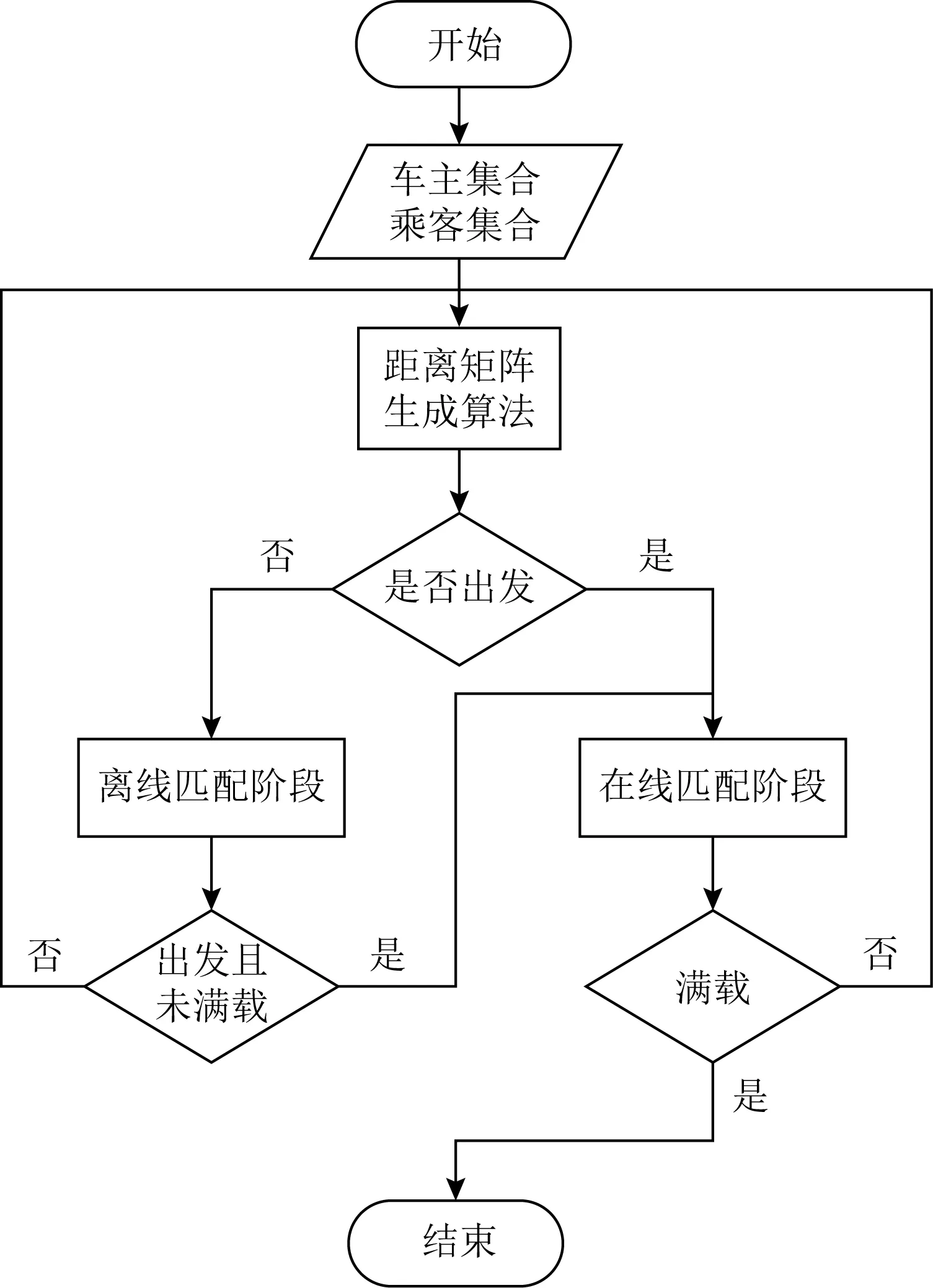
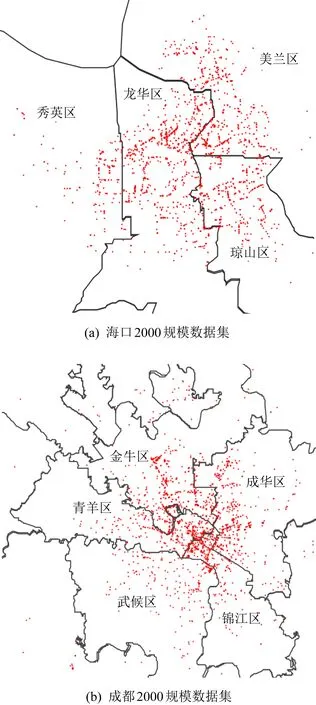
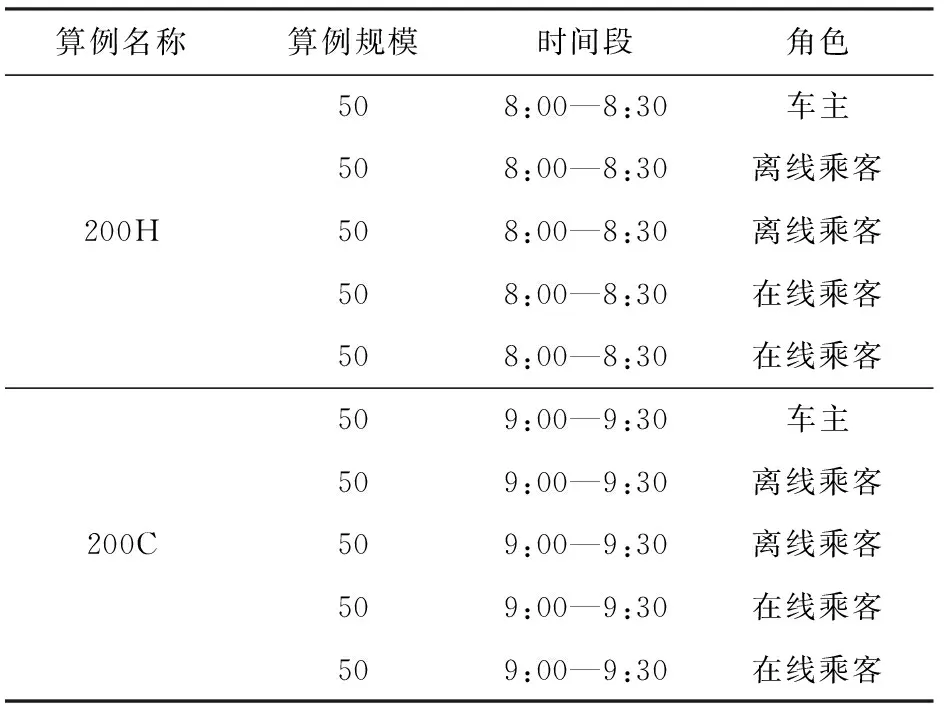
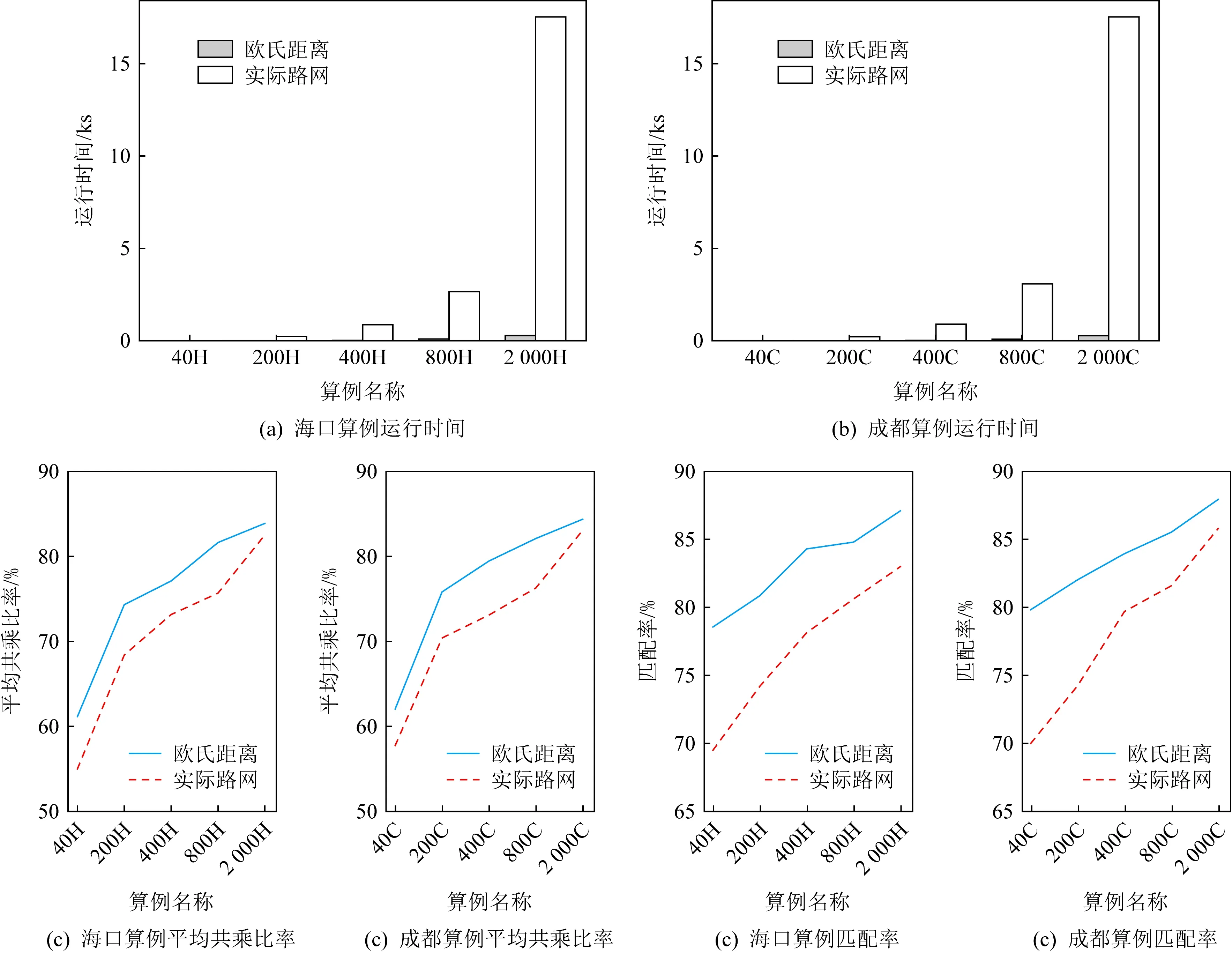
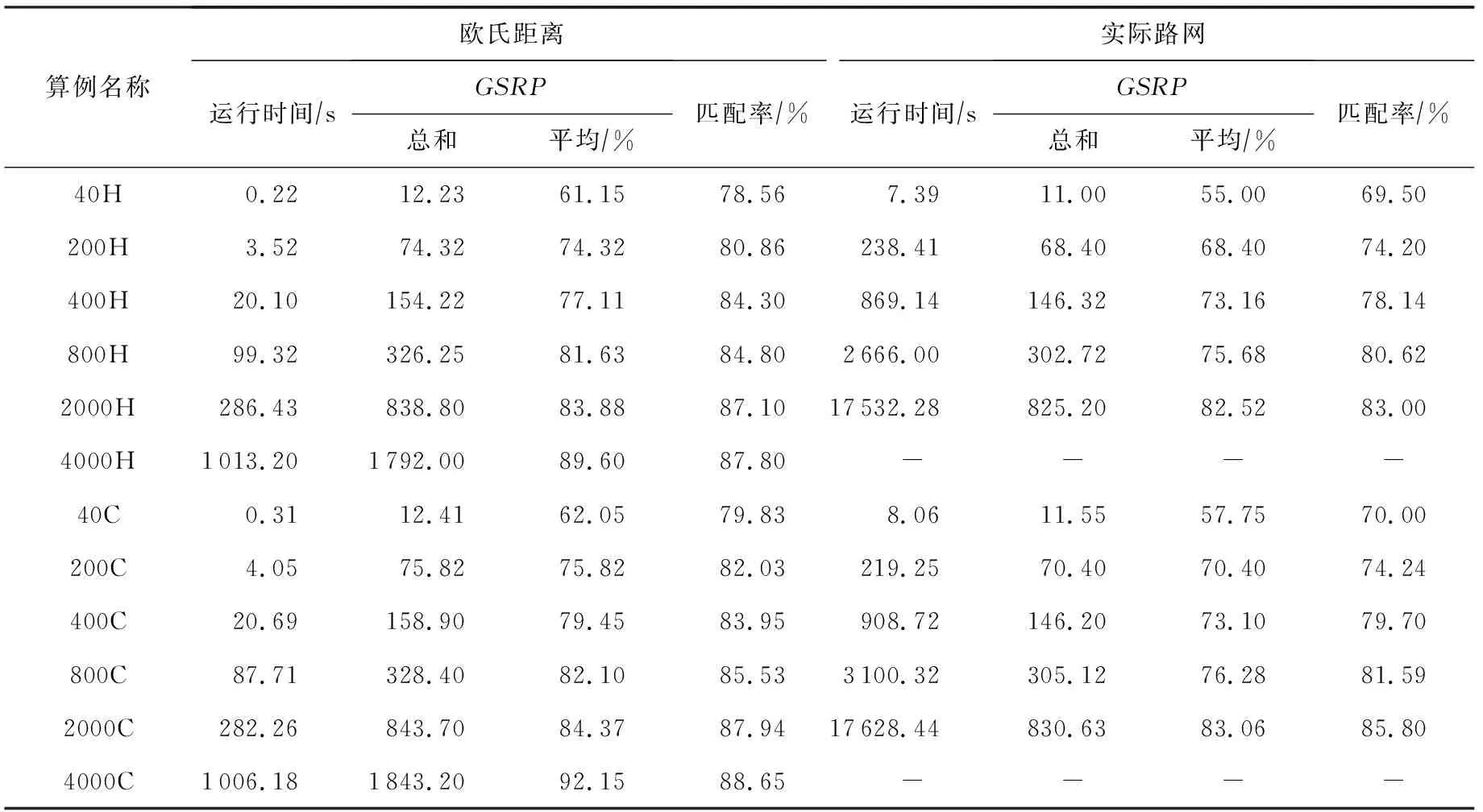
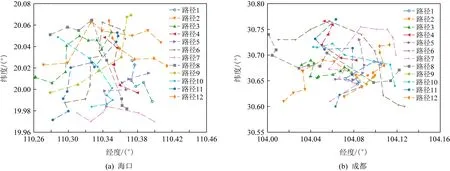
i (8) c≤Cdi. (9) 其中,式(7)限定了i和j的取值范围;式(8)中〈vi,vi+1,…,vj〉是1条有序的路径;式(9)是乘客数小于车辆的最大容量. 离线匹配阶段使用GSRP来评价车主共享资源的利用效率,并以绕行距离(detour length,DL)[34]对其进行约束,从而平衡车主共享效率和乘客订单可行性.车主与乘客的GSRP反映了乘客与车主的匹配价值.车主出行效益取决于乘客与之共乘的共享路径长短,因此,该值越大则表示车主的高匹配价值路程越长,车主的运输资源利用效率越高,反之则表示车主把大量路程浪费在独自行驶过程中,空载率越高,运输资源的利用效率越低. 定义4.标准路径L.L即为离线匹配阶段和在线匹配阶段在动态匹配过程中规划出的行驶路径,其距离为disL.车主的初始标准路径为未匹配乘客时的行驶路径Ld,其距离为disLd.同理,乘客的初始标准路径为其独自出行的行驶路径Lr,其距离为disLr.针对车主的绕行距离定义为dDL,针对共乘乘客的绕行距离定义为rDL,计算公式为: (10) 在线匹配阶段使用首尾距离度作为匹配标准,针对离线匹配后生成的标准路径,首尾距离度反映了在线匹配阶段待匹配乘客所在地和目的地是否在标准路径附近,以及距离车主所在地和目的地的远近,该值越大则表示待匹配乘客的路径与标准路径越接近,从而大大减小了车主更新标准路径的幅度和接送待匹配乘客的绕行距离. 定义5.首尾距离度(location to destination,LTD).LTD表示乘客r所在地和目的地分别与标准路径各个部分间以及车主所在地和目的地的最短距离加权和的倒数. 设有车主与乘客生成的标准路径L、待匹配乘客r、乘客所在地lrj与标准路径L各个部分间的最短路径Llr和乘客目的地arj与标准路径L各个部分间的最短路径Lar;乘客所在地lrj与车主所在地ldi间的最短路径Lldr和乘客目的地arj与车主目的地adi间的最短路径Ladr.为进一步提升算法求解效率,在离线匹配阶段未匹配到乘客的情况下,于在线匹配阶段使用单一首尾距离度进行评估,如式(11)所示;否则,使用复合首尾距离度进行评估,如式(12)所示. (11) (12) s.t.Larad∉L, (13) Lldlr∉L, (14) θ,η≤1,θ+η=1, (15) 其中,θ表示乘客r所在地和目的地与车主d所在地和目的地的距离系数,η表示乘客r所在地和目的地与标准路径的距离系数,距离系数在乘客距离标准路径的远近和乘客乘车的路程间做出权衡,车主可根据个人意愿设置2种距离系数来调整待匹配乘客集合.L表示离线匹配后生成的标准路径,Larad表示乘客r目的地之后对应的标准路径的部分,Lldlr表示乘客r所在地之前对应的标准路径的部分.式(13)表示在计算乘客r所在地到标准路径的最短距离时不计算目的地之后的部分路径Larad;式(14)表示在计算乘客r目的地到标准路径的最短距离时不计算所在地之前的部分路径Lldlr;式(15)限定了2种距离系数的取值范围.本文涉及的变量如表2所示: Table 2 Variables表2 变量表 双模式协作匹配算法在进行数学建模时将优化目标根据离线匹配阶段和在线匹配阶段不同的价值评估标准进行分析.离线匹配阶段以定义3中的通用共乘比率来评价车主与乘客的匹配价值,定义车主i与乘客j匹配价值为gij;在线匹配阶段以首尾距离度来评价对应的匹配价值,此时车主i和乘客j的匹配价值为wij.xij和yij分别表示离线匹配阶段和在线匹配阶段车主与乘客是否匹配.问题目标即为通过动态共乘匹配过程得出一种匹配方案使得所有车主乘客匹配对的价值总和最大.此时的目标函数为: (16) s.t.xij+yij≤1,∀i∈[1,m],∀j∈[1,n], (17) (18) (19) xij,yij∈{0,1},∀i∈[1,m],∀j∈[1,n], (20) dDL≤μ×disLd, (21) rDL≤μ×disLr, (22) Trj>Tdi(xij+yij), (23) D∩R=∅. (24) 其中:式(17)表示每名乘客与每名车主间只能在离线匹配阶段或在线匹配阶段匹配一次;式(18)表示每名乘客只能匹配到1名车主;式(19)表示每名车主在离线和在线匹配阶段匹配到的总乘客数应小于等于车容量;式(20)限定xij和yij的取值范围,0表示不匹配,1表示匹配;式(21)定义了车主的绕行距离,μ为绕行距离系数,约束车主的最大绕行距离;式(22)定义了共乘乘客的绕行距离,μ为绕行距离系数,约束乘客的最大绕行距离;式(23)表示待匹配乘客出发时间晚于车主出发时间;式(24)表示车主和乘客具有身份唯一性. 动态共乘匹配过程需对数以万计车主乘客集合进行全局匹配,对算法的求解效率和求解质量要求极高,主要面临3个求解难点: 1) 全局最优性.由于并发的车主乘客数量巨大,且在匹配后行驶过程中仍实时出现新车主和新乘客,故求解难度高,难以保证匹配速度与质量. 2) 共乘比率.在动态共乘匹配过程中,车主能够沿途匹配多个乘客,即车主乘客一对多问题.在面对一对多问题时,计算单车主单乘客匹配问题的传统共乘比率会变得异常复杂,因而无法获得较好的求解效果. 3) 动态实时性.在计算车主和乘客间的通用共乘比率时,由于实际路网数量巨大、复杂度高,同时需要规划出任一车主和乘客每段路径的最短路径,子路径规划难度高,故计算量巨大,无法保证算法的实时性. 本节针对数学建模阶段提出的研究难点提出相应的解决方案,设计了双模式协作匹配算法.于2.1节提出距离矩阵生成算法,在匹配前对乘客集合进行约束处理筛选出车主和对应的待匹配乘客集合,简化最短路径的计算复杂度和计算量,从而保障了后续匹配过程中的动态实时性;于2.2节离线匹配阶段中,针对动态车辆共乘问题中的全局最优化问题,提出了基于单条带权最短路径的带权路径搜索树,并根据带权路径搜索树提出了基于通用共乘比率的价值矩阵生成算法,解决了基于传统单车主单乘客共乘比率的价值矩阵生成算法在处理单车主多乘客时计算异常复杂的问题;于2.3节在线匹配阶段使用基于首尾距离度的价值矩阵生成算法来代替计算量巨大的基于共乘比率的价值矩阵生成算法.本算法总体框架如图1所示,总体流程如图2所示: Fig. 1 Bimodal cooperative matching algorithm frame图1 双模式协作匹配算法总体框架图 Fig. 2 Bimodal cooperative matching algorithm process图2 双模式协作匹配算法流程图 本节针对动态共乘匹配中在计算车主与乘客的匹配程度时计算量大以及存在大量对于当前车主无效的乘客集合的问题,提出2个解决方案: 1) 于匹配前为车主筛选出待匹配的乘客集合,无须计算复杂的实际路网,因此模型早期可在不花费大量计算开销的情况下筛选出部分待匹配乘客R.此阶段输出的是经过车主绕行距离约束和时间约束筛选的待匹配乘客集合Rd,待匹配乘客满足当前车主最基本的匹配约束. 2) 在计算GSRP和LTD时,最大的开销为循环计算待匹配乘客与标准路径上各节点间的最短距离,因此本文中采用算法1中的距离矩阵来存储最短距离,可很大程度上降低时间开销.距离矩阵生成算法根据已经得到的标准路径上各节点计算与待匹配乘客rj间的最短距离,在计算距离矩阵时使用上三角矩阵代替方阵,使得原本的时间消耗从O(m×n)降为O(m×n/2),最终得到距离矩阵U.距离矩阵生成算法见算法1. 算法1.基于约束时间窗和绕行距离约束的距离矩阵生成算法. 输入:车主集合D、乘客集合R和标准路径; 输出:车主的待匹配乘客集合Rd. ①d∈Dandr∈R; ②Dis_matrix(L,r)=U[d][r]; /*距离矩阵函数*/ ③M=N=[L,lr,ar]; ④ forminM.size ⑤ forninm ⑥ ifm==n ⑦u(m,n)=0; /*u为U[d][r]中的距离元素*/ ⑧ else ⑨u(m,n)=Euclidean_dis(m,n); ⑩ end if /*从距离矩阵中获得节点间的距离*/ /*超出车主最大绕行距离,不满足时间窗约束*/ /*从待匹配乘客集合中移除乘客r*/ 在离线匹配计算共乘比率过程中最大的计算开销为最短路径的计算.对于大型算例,Dijkstra算法和Floyd算法计算开销过大,本文使用欧氏距离代替实际路网距离计算,通过实验验证基于欧氏距离在共乘比率和匹配率方面不会产生较大误差,且能够提升算法求效率. (25) 如式(25)所示,任意2点间的欧氏距离小于或等于相同的2点间的实际路网距离,如乘客与车主间的欧氏距离不满足当前车主di的最大绕行距离约束,则无须计算实际路网距离,直接将该乘客排除在车主di的匹配范围之外. 动态共乘匹配过程由于并发的车主乘客数量巨大,且在匹配后行驶过程中仍实时出现新车主和新乘客,故很难解决全局最优性问题.针对此问题需高效计算得到车主与乘客的共乘比率,然而基于传统单车主单乘客的共乘比率计算方法无法解决动态共乘匹配过程中的多车主多乘客问题,因此本文的双模式协作匹配算法在离线匹配阶段主要提出2个解决方法: 1) 基于带权路径搜索树提出了通用共乘比率计算方法,依赖树形结构的高搜索效率和通用共乘比率的高求解质量来解决全局最优性问题和共乘比率问题. 2) 于离线匹配阶段根据匹配结果从带权路径搜索树中搜索得到匹配方案的最优路径,即为标准路径,使用标准路径进行下一次的动态匹配,下一名乘客的匹配过程建立在上一名乘客与车主匹配完成规划出的标准路径上,能够有效地提高乘客间的关联性从而进一步增大车主与乘客的匹配率,减小乘客的乘坐距离. 离线匹配阶段,车主与乘客的匹配为非实时过程,设计算法时更加偏向于考虑求解质量和匹配程度.离线匹配算法流程如图3所示. Fig. 3 Offline matching algorithm process图3 离线匹配算法流程图 设车主数量为m,乘客数量为n,以价值函数生成的m×n的价值矩阵为G,其中元素gij表示车主i和乘客j的价值.离线匹配算法基于带权路径搜索树,依赖树形结构的高搜索效率及GSRP带来的高求解质量.车主di通过共乘服务平台发布当前状态statusi,乘客rj通过共乘服务平台发布行程tripsj,共乘服务平台根据statusi和tripsj将车主和乘客执行算法1,得到车主di的待匹配乘客集合Rd,在车主绕行距离和车容量的约束下进行动态匹配.在计算此阶段的标准路径时,首先通过算法1求得初始标准路径上的点与待匹配乘客间的距离矩阵;然后根据算法2创建关于待匹配乘客rj和车主di的带权路径搜索树Tree,将待匹配乘客rj的所在地lrj和目的地arj以及车主di的所在地ldi和目的地adi定义为{key,value}: (26) 算法2.基于带权路径搜索树的通用共乘比率生成算法. 输入:车主集合D、待匹配乘客集合Rd; 输出:离线阶段标准路径. ① fordinD ② forrinR ③Dis_Matrix(d,r); ④ 初始标准路径L; ⑤Tree←Init_Tree(); /*初始化带权路径搜索树*/ ⑥Tree.root=ld; /*车主所在地为根节点*/ ⑦ldi.InsertChild()→ldi.cj=lrj; /*将乘客所在地插入到根节点,例: ⑧lrj.BrotherNode=lrj,j≠this j; /*乘客所在地节点的兄弟节点,例: ⑨Tree←InsertNode(); ⑩ whilek≤2(c+2) andarj.leaf= False do /*为乘客的所在地节点插入子节点,例: /*为乘客的目的地节点插入子节点,例: /*节点的权重等于累计节点权重*/ /*共乘路径和车主行驶总路径*/ /*gij为G中的元素*/ 以ldi为根节点,按照算法2的规则依次插入乘客的所在地lrj和目的地arj,形成搜索树的所有swp=〈v1,v2,…,v2(c+1)〉,从带权路径搜索树中获得单条带权最短路径,即为当前已匹配乘客生成的标准路径,由定义3可得GSRP,从而求得待匹配乘客和车主的价值矩阵G,由KM算法求解价值矩阵G,得到最优匹配方案.当前未匹配乘客和新进入的待匹配乘客组成下一次的输入乘客集合,循环执行直至满载或者进入在线匹配阶段.非实时的离线匹配阶段结束后,得到一条离线匹配阶段动态规划的标准路径. 动态匹配过程中的实时匹配过程对匹配的动态实时性要求极高,算法需要同时兼顾全局最优化、共乘比率和动态实时性,然而在计算车主和乘客间的共乘比率时,由于实际路网数量巨大、计算复杂度高,同时需要规划出任一车主和乘客每段路径的最短路径,子路径规划难度高,故计算量巨大,无法保证算法的实时性.因此本文的双模式协作匹配算法在线匹配阶段主要提出3个解决方法: 1) 使用首尾距离度代替计算消耗巨大的通用共乘比率作为价值评估标准,首尾距离度综合考虑乘客的所在地和目的地与车主行驶的标准路径间的最短距离以及乘客所在地和目的地与车主的所在地和目的地间的最短距离,使用欧氏距离代替实际路网进行计算,能够在保证匹配率和共乘比率的前提下高效地计算出匹配结果. 2) 根据离线匹配阶段得到的标准路径和匹配方案选择使用单一首尾距离度或者复合首尾距离度来进一步提高匹配率,从而满足动态共乘在线阶段的实时性要求. 3) 根据在线匹配阶段的匹配方案使用实时订单插入算法将当前匹配到的乘客的出发地和目的地实时地更新到标准路径. 以下为在线匹配阶段设计过程:在线匹配阶段中针对离线匹配阶段生成的标准路径,若车主已匹配到乘客但处于未满载状态,为扩大车主di的共乘比率,车主di在行驶过程中继续匹配沿途的乘客rj,根据车主当前的statusi和乘客发布的tripsj进行在线匹配阶段的匹配过程,由于车主与乘客的匹配过程实时进行,因此需着重考虑算法的求解效率,使用基于首尾距离度的价值矩阵生成算法计算车主di和待乘客的LTD,从而求得待匹配乘客和车主的价值矩阵W,由KM算法求解价值矩阵W,得到最优匹配方案,并使用实时订单插入算法将当前匹配到的乘客的出发地和目的地实时地更新到标准路径,车主按照实时规划的路径行驶.在线匹配算法流程如图4所示: Fig. 4 Online matching algorithm process图4 在线匹配算法流程图 由于标准路径是通过车主所在地和目的地的当前最短路径,如车主选择接送所在地和目的地均靠近标准路径的乘客,因此车主在接送新乘客时不会产生较大的绕行距离,从而在增加乘客的同时扩大共乘比率.在计算待匹配乘客与标准路径各部分间最短距离时,如乘客的投影点不在标准路径上,则此时计算首尾距离度需考虑额外的绕行距离.具体的路径分析如图5和图6所示. Fig. 5 The distance between a rider and the standard path图5 乘客与标准路径间的距离 Fig. 6 Distance analysis between a rider and standard path图6 乘客与标准路径间的距离分析 如图5所示,经离线匹配后得到一条标准路径: L=〈ld,lr1,ar1,ad〉, (27) 此时乘客r2进行匹配,在到达目的地之前r2所在地与标准路径有2个投影点P1和P2,在所在地之后r2目的地与标准路径有2个投影点P3和P4. 乘客r2所在地与路径〈ld,lr1〉间的距离为dis(lr2,ldlr1);r2所在地与路径〈lr1,ar1〉间的距离为dis(lr2,lr1ar1)+dis(P2,lr1),其中dis(P2,lr1)为额外绕行距离,此时乘客r2所在地与标准路径的最短距离为dis(lr2,ldlr1). 乘客r2目的地与路径〈lr1,ar1〉间的距离为dis(ar2,lr1ar1);r2目的地与路径〈ar1,ad〉间的距离dis(ar2,ar1ad).此时乘客r2目的地与标准路径的最短距离为dis(ar2,ar1ad). 为了在实时匹配阶段更好地节省计算资源,在保证匹配结果的前提下,此处只计算到达乘客r目的地前与标准路径各部分的最短距离和乘客r所在地后与标准路径各部分的最短距离,从而避免了出现反向接送乘客的现象. 如图6所示,可通过式(28)(29)计算乘客与标准路径间的最短距离.连接部分标准路径AB和乘客r得到一个三角形,如△rAB和△rBA是直角三角形或者锐角三角形,最短距离为乘客r距离AB的直线距离,否则需考虑额外绕行距离. 乘客r所在地与标准路径的最短距离: (28) 乘客r目的地与标准路径的最短距离: (29) 设车主数量为m,乘客数量为n,经过离线匹配后得到车主的当前状态statusi和乘客行程tripsj,以价值矩阵生成算法生成m×n的价值矩阵W,其中元素wij表示车主i和乘客j的匹配价值.单一首尾距离度矩阵生成算法如算法3所示: 算法3.单一首尾距离度价值矩阵生成算法. 输入:车主集合D、待匹配乘客集合Rd; 输出:单一首尾距离度价值矩阵W. ① 初始化价值矩阵W; ② fordinD ③ forrinR ④Dis_Matrix(r,Ld); /*此时标准路径为车主原行驶路径*/ ⑤Llr=shortest_path(lrj,Ld); /*乘客所在地与标准路径最短距离*/ ⑥Lar=shortest_path(arj,Ld); /*乘客目的地与标准路径最短距离*/ /*wij为W[d][r]中的元素*/ ⑧W[d][r]=wij; /*单一首尾距离度矩阵*/ ⑨ end for ⑩ end for 标准路径作为引导线来计算复合首尾距离度,旨在确保匹配到的乘客在标准路径附近.综合考虑离线匹配阶段得出的匹配方案和标准路径,单一首尾距离度矩阵生成算法只选择乘客所在地和目的地与标准路径间的最短距离和的倒数作为首尾距离度,具有较高的求解效率,可用于离线匹配阶段未匹配到乘客的情况.但对于离线匹配阶段已匹配到乘客并生成了标准路径的情况,在进行乘客路径的更新时可能导致标准路径发生较大的变动,从而增加不必要的低效路程.故对于已匹配到乘客的情况,在线匹配阶段采用复合首尾距离度作为评估标准,且绕行距离约束仍然有效. 算法4.复合首尾距离度价值矩阵生成算法. 输入:车主集合D、待匹配乘客集合Rd; 输出:单一首尾距离度价值矩阵W. ① 初始化价值矩阵W; ② fordinD ③ forrinR ④Dis_Matrix(r,Ld); /*此时标准路径为车主原行驶路径*/ ⑤Llr=shortest_path(lrj,Ld); /*乘客所在地与标准路径最短距离*/ ⑥Lldr=shortest_path(lrj,ldi); /*乘客所在地与车主所在地最短距离*/ ⑦Lar=shortest_path(arj,Ld); /*乘客目的地与标准路径的最短距离*/ ⑧Ladr=shortest_path(arj,adi); /*乘客目的地与车主目的地最短距离*/ /*wij为W[d][r]中的元素*/ ⑩W[d][r]=wij; /*复合首尾距离度矩阵*/ 定义fjk为把匹配乘客rj插入到标准路径中使目标函数增长最大的位置后目标函数的改变量. 实时订单插入算法的核心思想为将已匹配乘客插入到能使目标函数增长最大的位置.算法5描述为: 算法5.实时订单插入算法. 输入:W; 输出:标准路径. ① 选择wijinW: ② s.t.wij=max(wij); ③i∈[1,m]∩,j∈[1,n]∩; ④ if (j,L)arg maxfjL ⑤ 将乘客rj更新到标准路径; ⑥ end if 迭代执行算法5,将已匹配到的乘客插入到标准路径中,直至车辆满载或已无可选乘客. 本文使用海口市和成都市双数据集进行实验,通过算法的求解速度和求解质量进行评估.实验仿真语言为Python3.7,运行环境为Intel®CoreTMi7-10750H CPU @ 2.60 GHz 2.59 GHz,16 GB RAM. 实验数据集基于滴滴出行盖亚数据开放计划(didi chuxing gaia initiative),数据范围涵盖海口市和成都市车主乘客全天出行轨迹数据,自出行轨迹数据中随机选取40/200/400/800/2000/4000名参与者,并随机指定50%为车主,50%为乘客,其中海口市和成都市2000数据规模的模拟分布如图7所示. Fig. 7 Distribution of drivers and riders图7 车主和乘客分布图 由于数据集本身密集程度对实验参数和实验结果的影响较大,因此采用海口市和成都市双数据集生成算例对实验结果进行评估,算例属性由表3 Table 3 Properties of Instance表3 算例属性表 可知.此处只列举了规模为200的算例,其余算例分别命名为40H/40C,400H/400C,800H/800C,2000H/2000C,4000H/4000C,其中,数字表示数据规模,H和C分别表示海口市数据集和成都市数据集. Fig. 8 Comparison between Euclidean distance and actual distance图8 欧氏距离与实际路网对比图 3.2.1 欧氏距离与实际路网距离对比 动态共乘匹配过程对算法求解的实时性要求极高,面对大规模需要计算最短路径的数据时,实际路网距离需要花费大量路网计算开销,很难满足实时性,因此本文使用欧氏距离进行计算,并对基于欧氏距离的本文算法和使用Dijkstra算法计算实际路网距离的本文算法的实验结果进行评估. 本文通过对海口市和成都市40H/40C,200H/200C,400H/400C,800H/800C,2000H/2000C,4000H/4000C规模的算例使用基于欧氏距离的双模式协作匹配算法和基于实际路网距离的双模式协作匹配算法进行对比,其中海口市和成都市实际路网数据从OpenStreetMap获得,实际路网数据集包含海口市45 417个节点和48 080条边,成都市37 853个节点和40 758条边,实验结果表明所需求解的平均通用共乘比率、匹配率和匹配方案差异较小.实验参数为μ=1.5,θ=0.4,η=0.6.实验结果如图8和表4所示. 1) 从图8所示的算法运行时间对比图可知,基于实际路网距离的本文算法在处理不同规模的数据时耗时明显高于基于欧氏距离的本文算法,且在处理大规模数据集时运行时间呈现出异常的增长态势,无法满足动态车辆共乘的实时性要求.由表4可知:基于欧氏距离的本文算法和基于实际路网距离的本文算法在处理海口市数据集不同规模算例时平均运行时间为81.91 s和4262.64 s,前者仅为后者的1.92%;基于欧氏距离的本文算法和基于实际路网距离的本文算法在处理成都市数据集不同规模算例时平均运行时间为79.00 s和4 372.96 s,前者仅为后者的1.81%. 2) 从图8所示的海口市和成都市双数据集实验结果可知,在平均通用共乘比率和匹配率方面,基于欧氏距离的本文算法实验结果与基于实际路网的本文算法实验结果差异较小.由表4可知:基于欧氏距离的本文算法和基于实际路网距离的本文算法在处理海口市数据集不同规模算例时平均通用共乘比率分别为81.75%和78.70%,平均匹配率为83.12%和77.09%,平均相差4.54%;基于欧氏距离的本文算法和基于实际路网距离的本文算法在处理成都市数据集不同规模算例时平均通用共乘比率82.51%和79.29%,平均匹配率为83.85%和78.26%,平均相差4.41%. 3) 需要指出,在处理算例为4000H/4000C时,基于实际路网距离的算法求解时间已经完全无法满足动态共乘匹配,因此表4只列出了基于欧氏距离的实验结果,在进行平均通用共乘比率、平均匹配率和平均运行时间对比时也是基于2种数据集前5组算例的实验结果. Table 4 Comparison Between Euclidean Distance and Actual Distance表4 欧氏距离与实际路网对比表 Fig. 9 Comparison of running time between improved distance matrix and normal distance matrix图9 改进距离矩阵与普通距离矩阵的运行时间对比 3.2.2 距离矩阵生成时间对比 在计算距离矩阵时使用上三角矩阵代替方阵的生成,改进后的距离矩阵生成算法与普通距离矩阵生成算法的时间比较由图9和表5可知.表5记录了海口市和成都市双数据集下车主乘客对数量、普通距离矩阵生成方法和改进距离矩阵生成算法的运行时间. 由图9和表5的实验结果可知,改进后的距离矩阵生成算法在处理海口数据集和成都数据集时均表现出较好的结果,各组算例中改进算法的运行时间平均为普通算法的53%. Table 5 Running Time Between Improved Distance Matrix and Normal Distance Matrix表5 改进距离矩阵与普通距离矩阵的运行时间 s Fig. 10 Result of sole offline matching图10 单纯离线匹配模式结果 3.2.3 价值矩阵生成时间对比 本节对比单纯离线匹配模式、单纯在线匹配模式和双模式协作匹配算法3种不同模式下算法的运行时间和匹配率.本文提出的双模式协作匹配算法采用离线匹配模式和在线匹配模式相结合的混合模式.实验参数为:绕行距离系数μ=1.5,算例为200H/200C.实验结果见图10~12和表6. Fig. 11 Result of sole online matching图11 单纯在线匹配模式结果 由图10可知单纯离线匹配模式在海口市和成都市双数据集下的评估表现.本模式下,平均匹配率为93.71%.单纯离线匹配模式下本文提出了基于带权路径搜索树的通用共乘比率算法,考虑乘客之间的关联性,乘客的匹配建立在前一名乘客与车主已经形成的标准路径的基础上,从而兼顾车主的通用共乘比率和已匹配乘客的绕行距离.在匹配次数较少时,此模式的运行时间较短,但是随着匹配乘客逐步增加,标准路径增长,算法的运行时间较长,不能满足即时匹配的要求,因此,单纯离线匹配模式适用于非即时的预约单处理. 由图11可知单纯在线匹配模式在海口市和成都市双数据集下的评估表现.单纯在线匹配模式下本文提出了基于首尾距离度匹配价值评估标准代替需要大量计算开销的通用共乘比率,针对离线匹配结果设计了单一首尾距离度和复合首尾距离度2种评估方式,使用实时订单插入算法将乘客插入标准路径,该方案具有较快的处理速度,但是平均匹配率为46.78%,仅为单纯离线匹配模式匹配率的49.91%.因此,单纯在线匹配模式更加适用于即时订单处理. 由图10和图11可知,单纯离线匹配模式具有高匹配率和低匹配速率的特性,单纯在线匹配模式具有高匹配速率和低匹配率的特性,因此,根据实际情况将二者结合成为一种双模式协作匹配算法,该模型包含离线匹配阶段和在线匹配阶段,在处理非即时的预约单时具有高匹配率且能兼顾匹配速率,在处理即时的实时单时具有高匹配速率.由图12可知双模式协作匹配算法在海口市和成都市双数据集下的评估表现,该图记录了双模式协作匹配算法的连续4次匹配过程.在匹配时间方面,双模式协作匹配算法前2次匹配为离线匹配阶段,因此匹配时间较单纯在线匹配模式有一定的增长;后2次匹配为在线匹配阶段,针对即时性订单具有较快的匹配效率,较单纯离线匹配模式匹配时间有了显著降低.在匹配率方面,离线匹配阶段使用通用共乘比率和标准路径来增加乘客间的关联性,因此匹配率较单纯在线匹配模式有了显著提升;在线匹配阶段针对前2次离线匹配阶段生成的标准路径进行在线匹配,每一名乘客的匹配建立在前一名乘客与车主形成的标准路径的基础上.因此,在离线阶段和在线阶段的双模式的协作匹配下,在线匹配阶段的匹配率较单纯在线匹配阶段的匹配率有了一定增长. Fig. 12 Result of bimodal cooperative matching algorithm图12 双模式协作匹配算法结果 Table 6 Comparison of Sole Offline Matching, Sole Online Matching and Bimodal Cooperative Matching Algorithm 实验对比数据由表6可知,单纯离线匹配模式在双数据集下,前2次的匹配过程平均运行时间为1.59 s,平均匹配率为89.08%;后2次匹配过程的平均运行时间为607.15 s,平均匹配率为98.24%.由此可看出单纯离线匹配模式只有在匹配次数较小时能够兼顾运行时间和匹配率. 单纯在线匹配模式在双数据集模式下,前2次的匹配过程平均运行时间为0.43 s,平均匹配率为45.92%;后2次匹配过程平均运行时间为0.74 s,平均匹配率为47.65%.单纯在线模式的平均匹配率为单纯离线匹配模式的49.91%.本文采用的双模式协作匹配算法的在海口市和成都市2个数据集下都能够兼顾匹配率和匹配速度,在算法运行时间和求解质量上有着显著的效果,平均运行时间为0.79 s,仅为单纯离线匹配模式下的0.26%,平均匹配率为85.53%,相较于单纯在线匹配模式提升了82.83%. 3.2.4 双模式协作匹配算法 本节介绍双模式协作匹配算法在不同数据规模下的运行结果.实验参数为:绕行距离系数μ=1.5,复合首尾距离度的距离系数θ=0.4,η=0.6.表7记录了成都市数据集不同算例在离线匹配阶段的GSRP的平均值、GSRP超过80%和90%的比率、绕行距离、共乘距离和行驶距离,以及在线匹配阶段的LTD. 分析表7可知,双模式协作匹配算法的平均GSRP为84.86%.数据规模在800以下时离线匹配阶段的54.25%的平均GSRP低于0.8;数据规模在4 000以下时离线匹配阶段的50.50%低于0.9.离线匹配阶段GSRP超过80%和90%的比率与数据规模呈正相关. Table 7 Bimodal Cooperative Matching Algorithm in Different Data Sizes表7 不同数据规模的双模式协作匹配算法 3.2.5 参数敏感性分析 本节分析了离线匹配模式下绕行距离系数对算法运行时间、平均GSRP和匹配率的影响以及在线匹配模式下距离系数对算法运行时间、LTD和匹配率的影响,实验算例为200H,实验结果如图13所示. 在离线匹配模式下,随着绕行距离的增大,算法的运行时间呈下降趋势,匹配率和平均GSRP呈上升趋势;在线匹配模式下,随着距离系数θ的增大和η的减小,算法的运行时间呈上升趋势,LTD逐渐减小,匹配率先呈上升趋势后逐渐下降,在θ=0.4且η=0.6时达到峰值,此时的平均匹配率为82.53%. 3.2.6 路径演示 本节通过路径演示分析实验结果的可行性和准确性.实验算例为200H/200C,实验参数为μ=1.5,θ=0.4,η=0.6.图14为离线匹配阶段双数据集实验结果中单条路径演示;图15为增加了在线匹配阶段的双模式协作匹配下双数据集实验结果中单条路径演示;图16为双模式协作匹配下双数据集实验结果总体的路径演示. 分析离线匹配阶段的单条路径和双模式协作匹配算法下的单条路径演示可知,离线匹配后通过在线匹配可有效地为车主匹配到新的高匹配价值乘客,并证明了在线匹配阶段增加乘客时离线匹配阶段规划的标准路径未产生较大的变动.合理地将乘客插入到标准路径中,表明本文算法求解具有较高的质量和实用性. 本节对双模式协作匹配算法与一种较新的自适应搜索策略[1]进行实验比较求解效率和质量.实验参数为μ=1.5,θ=0.4,η=0.6.表8记录了成都市不同规模数据集、双模式协作匹配算法的离线匹配阶段和在线匹配阶段2个阶段的运行时间、匹配率和GSRP,以及自适应搜索策略2个阶段的运行时间和SRP. 动态共乘问题主要存在全局最优性、共乘比率和动态实时性等方面的挑战.本文综合考虑时间约束、绕行距离、运行时间和匹配率,并且证明本文算法在运行时间和共乘比率方面优于其他算法.具体对比分析和结果为: 1) 在双模式协作匹配算法的离线匹配阶段,基于带权路径搜索树定义了通用共乘比率,解决了自适应搜索策略中使用的传统共乘比率算法在面对单车主多乘客时计算异常复杂的问题.由表8可知,在500对规模下,本文算法平均共乘比率为80.14%,双模式协作算法的总体平均共乘比率为77.32%,自适应搜索策略的总体平均共乘比率为59.62%,仅为双模式协作匹配算法总体平均共乘比率的77.11%. 2) 在双模式协作匹配算法的在线匹配阶段,采用首尾距离度代替自适应搜素策略中传统的共乘比率算法作为价值评估标准,并根据离线匹配阶段得到的标准路径和匹配方案选择使用单一首尾距离度或者复合首尾距离度来进一步提高匹配率,从而保证了在线匹配阶段的实时性.由表8可知,在不同数据规模下本文模型的运行速度相较于自适应搜索策略有较大的提升.在10对算例下,本文算法平均运行时间仅为自适应策略的4.10%;在500对算例下,本文算法平均运行时间仅为自适应搜索策略的45.43%.本文算法总体平均运行时间仅为自适应搜索策略的44.86%. Fig. 13 Parameter sensitivity analysis图13 参数敏感度分析 Fig. 14 Offline matching stage single route demonstration图14 离线匹配阶段单条路径演示 Fig. 15 Bimodal cooperative matching algorithm single route demonstration图15 双模式协作匹配算法单条路径演示 Fig. 16 Bimodal cooperative matching algorithm partial geographical demonstration图16 双模式协作匹配算法部分路径演示 Table 8 Comparison of the Results of Bimodal Cooperative Matching Algorithm and Adaptive Strategy 3) 自适应搜索策略中并未考虑匹配率,因此只列出了本文模型的平均匹配率.双模式协作匹配算法在离线匹配阶段的不同数据规模下平均匹配率为98.36%,在线匹配阶段的不同数据规模下平均匹配率为67.36%,在不同数据规模下的总体平均匹配率为82.86%. 本文提出了一种基于离线匹配和在线匹配的双模式协作匹配算法.首先,对待匹配的乘客进行约束处理,以筛选满足约束的车主乘客对,并对距离矩阵的生成方式进行了改进;其次,在离线匹配阶段,提出了一种基于带权路径搜索树的通用共乘比率生成算法;再次,于在线匹配阶段提出了2种基于首尾距离度的实时订单插入算法,采用了一种便于计算且具有较好评估能力的评估标准进行匹配价值评估;最后,通过实验对单纯离线匹配模式、单纯在线匹配模式和双模式协作匹配算法进行比较,并将双模式协作匹配算法与自适应搜索策略进行比较.实验表明,本文提出的双模式协作匹配算法具有较高的实用价值,兼顾算法求解效率和求解质量,并且在运行时间和匹配率上均比自适应搜索策略更具有优势.此外,基于双模式的匹配算法通过增加有效共乘路程,降低了车辆空载率,从而大幅提升了交通资源利用率和运输效率. 需要指出的是,本文提出的双模式协作方式仍较为单一,在离线匹配和在线匹配的转换方面还存在优化的空间.后续研究将探索对双模式协作的拓展方法,考虑使用强化学习和超启发式算法提升离线模式和在线模式动态转换的自主性和智能性,从而进一步提升匹配效率和匹配质量. 作者贡献声明:郭羽含负责方法设计、结构设计和论文修改;刘永武负责实验实现和论文初稿撰写.
1.2 优化目标
2 双模式协作匹配算法
2.1 距离矩阵生成算法
2.2 离线匹配阶段

2.3 在线匹配阶段


3 实验与分析
3.1 算 例
3.2 匹配实验结果分析

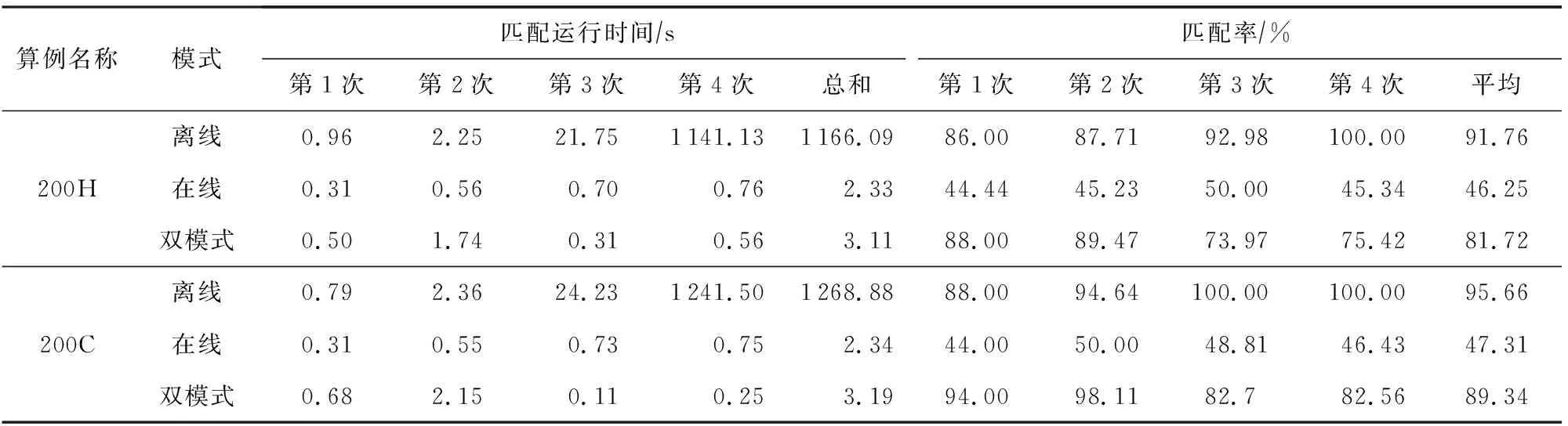
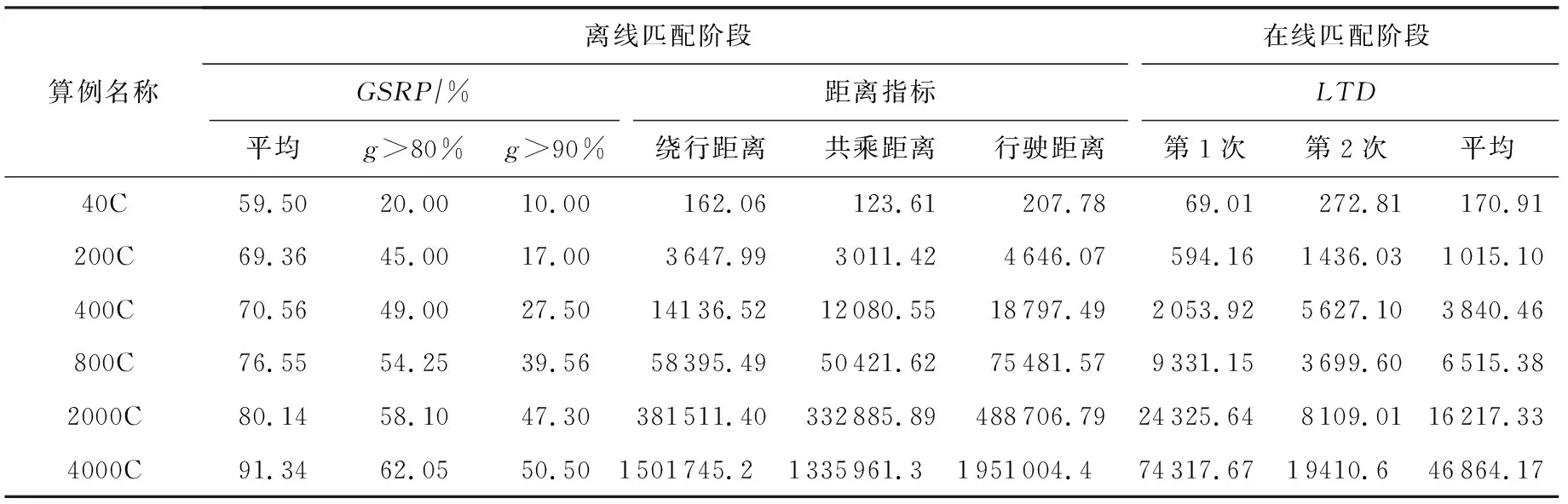
3.3 对比实验
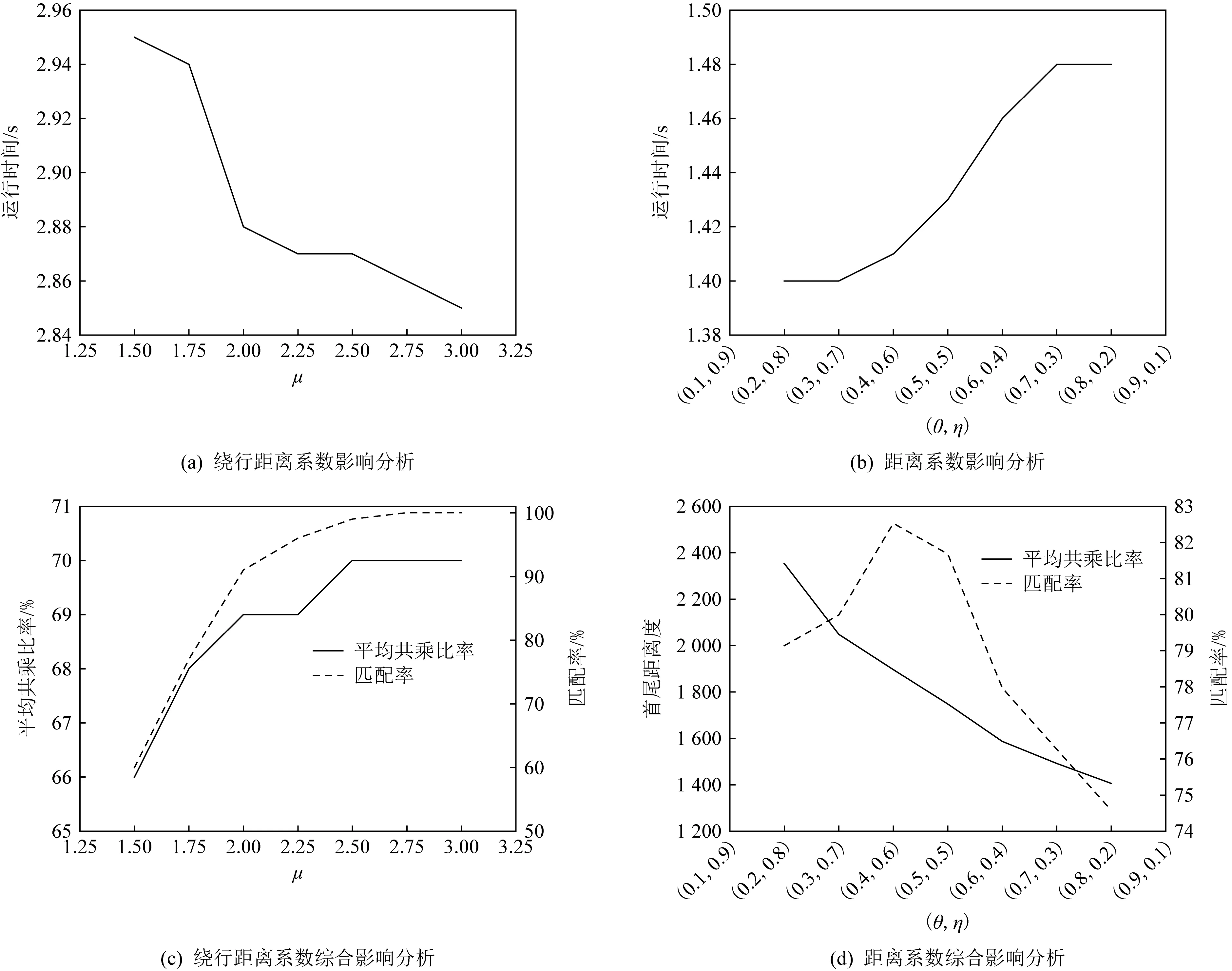

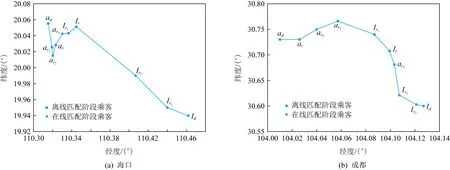

4 总结与展望
