基于图卷积的异质网络节点分类方法

谢小杰 梁 英 王梓森 刘政君

1(中国科学院计算技术研究所泛在计算系统研究中心 北京 100190) 2(中国科学院大学计算机科学与技术学院 北京 100049) 3(移动计算与新型终端北京市重点实验室(中国科学院计算技术研究所) 北京 100190)

近年来，图神经网络受到了研究者的广泛关注.通过端到端的方式对不规则网络结构(非欧氏空间)进行分析和挖掘，图神经网络能够有效揭示网络中的节点特征、关系特征和网络结构等隐含语义信息，生成上下文相关的节点表示，在知识图谱、社交网络、推荐系统等方面发挥了重要作用[1].

节点分类是图神经网络最重要的下游任务之一，目的是利用已标注节点学习网络语义信息，生成节点特征表示，识别未标注节点的类别[2].例如，在引文网络中，节点表示文献，文献引用构建了节点间的连接关系，通过学习文献的文本和引用关系特征，可以生成文献的特征表示，预测文献的研究主题[3].

图神经网络节点分类主要分为同质网络节点分类和异质网络节点分类.同质网络仅包含一种节点类型，且节点间的连接关系单一，如引文网络[3]中文献间的引用关系、协作网络[4]中学者间的合作关系和社交网络[5]中用户间的关注关系等.而现实世界中的数据关系复杂多样，构成的网络更多是异质网络，它包含多种类型的节点和关系，不同类型的节点以及节点间的关系揭示了不同的语义信息.例如，在学术网络[6]中，除了文献间的引用关系外，还包括学者与文献间的写作关系、文献与期刊间的发表关系等.

图神经网络能够利用网络中丰富的语义信息和全面的结构信息进行精准的节点分类，但是现有研究在节点分类上仍然面临着2个挑战：

1) 如何充分利用异质网络中丰富的语义信息，提升节点分类的效果.同质网络仅包含一种节点类型和关系类型，语义信息单一，在建模复杂数据关系上存在明显的局限性.异质网络由多种类型的节点和关系组成，语义信息丰富，能够有效描述多样化的数据特征.充分利用异质网络的多语义信息开展研究，可以适应更加复杂的数据场景.

2) 如何充分利用网络中全面的结构信息，学习合理的节点特征表示.异质网络结构复杂，仅使用对称元路径[6]揭示网络中同类型节点间的内在联系，不能充分发现邻居节点的相关性，需要引入邻居节点权重，结合节点特征、关系特征、邻域特征等全面的网络结构信息进行分析，区分不同邻居节点的重要性，生成更合理的节点表示，提升节点分类效果.

为应对上述2个挑战，本文提出了一种基于图卷积的异质网络节点分类框架(heterogeneous network node classification framework, HNNCF)，用于解决异质网络上的节点分类问题.首先，约简异质网络，将异质网络转换为语义化同质网络，简化网络结构并保留异质网络的多语义信息；然后，基于图神经网络中的消息传递框架，设计图卷积节点分类方法，在语义化同质网络上学习合理的邻居权重，生成节点异质语义表示，并利用节点异质语义表示识别节点的类别标签.同时，分别在3个公开数据集上，对本文设计的异质网络约简方法和图卷积节点分类方法进行了实验对比和分析，结果表明本文所提方法有效提升了节点分类效果.

本文的主要贡献包括3个方面：

1) 提出了一种基于图卷积的异质网络节点分类框架(HNNCF)，通过将异质网络约简为语义化同质网络，并利用消息传递框架实现图卷积节点分类，有效地解决了异质网络上的节点分类问题.

2) 提出了一种异质网络约简方法，结合对称元路径和关系表示池化函数，设计转换规则，生成语义化同质网络，简化了异质网络结构，保留了丰富的语义信息，便于适应消息传递框架.

3) 提出了一种图卷积节点分类方法，基于消息传递框架，计算无1-sum约束的邻居节点权重，加权聚合邻域特征，生成节点语义表示，充分利用了语义化同质网络的结构信息，进一步提升了分类效果.

1 相关工作

图神经网络能够充分利用网络中丰富的语义信息和全面的网络结构信息，以端到端的方式学习任务相关的节点表示，解决节点分类等问题.根据网络类型的不同，可将图神经网络节点分类的方法分为同质图神经网络方法和异质图神经网络方法.

在同质图神经网络方法中，Tomas等人[3]提出了一种图卷积网络(graph convolution network, GCN)，通过编码一阶邻域结构学习节点表示，综合利用了网络结构和节点特征信息，提升了节点分类效果.由于GCN无法适应大规模动态网络，Hamilton等人[7]提出了一种图神经网络框架GraphSAGE(graph sample and aggregate)，对中心节点的高阶邻域进行采样，结合不同的池化方式聚合邻域特征，提升了分类性能.Velickovic等人[8]认为不同邻居节点具有不同的重要性，提出了图注意力网络(graph attention network, GAT)学习邻居节点权重，通过多头注意力对邻域特征进行加权聚合，生成了更加合理的节点表示，获得了比GraphSAGE更好的分类效果.为了学习同质网络中潜在的关系特征，Wang等人[9]提出了一种邻边卷积方法，通过节点特征表示的差异性体现关系特征，将关系包含的语义信息融入到了节点表示学习中.Gilmer等人[10]提出了一种通用的消息传递神经网络(message passing neural network, MPNN)，对现有的图卷积网络进行了泛化，通过消息传递规则和聚合函数学习节点表示，有效建模了节点特征、关系特征和邻域结构等网络信息.虽然同质图神经网络节点分类方法能够充分学习网络结构特征，但是仅能建模单一语义关系，无法直接运用在异质网络中.因此，现有研究更关注于异质图神经网络方法，以充分利用网络语义信息，适应复杂的数据场景.

异质图神经网络方法重点关注网络结构和语义关系建模.异质网络结构由不同类型的节点和关系组成，表达了复杂数据的信息交互，融入异质结构特征有利于提升下游任务效果.在网络结构建模方法中，为了充分利用邻域结构信息，异质图神经网络(heterogeneous graph neural network, HetGNN)方法[11]提取了属性、文本、图片等异质邻居节点特征，结合注意力机制[12]生成包含丰富特征的节点表示.与HetGNN方法不同，Hu等人[13]提出了一种异质网络Transformer框架，通过时序编码和图采样对大型动态异质网络进行预训练，提取异质网络结构特征，提升节点分类等任务的效果.Yun等人[14]从结构生成的角度出发，提出了一种端到端的异质网络生成框架图变换网络(graph transformer networks, GTN)，通过邻接矩阵学习软选择机制，构建新的网络结构用于节点表示学习.异质网络语义信息主要通过关系类型和关系组合表达，建模多语义关系，能够有效揭示丰富的语义信息.在语义关系建模方法中，为了减少异质网络建模的复杂性，异质图注意力网络(heterogeneous graph attention network, HAN)方法[15]通过对称元路径将异质网络分解为多个表达不同语义关系的同质网络，并利用GAT聚合邻域特征，综合考虑了不同邻居节点的重要性.陈亦琦等人[16]提出了一种复合关系图卷积网络(composite relation graph convolution network, CRGCN)，通过建模属性网络中用户-属性等基本关系和用户-属性-用户等复合关系，学习编码关系特征的节点表示.Vashishth等人[17]提出了一种多关系图神经网络框架(composition-based multi-relational graph convolutional networks, CompGCN)，根据不同关系类型和邻居类型设置不同的组合算子，通过聚合邻域特征学习节点特征表示.异质网络结构复杂多样，直接建模难度较高，与网络结构建模方法相比，语义关系建模方法可以简化异质网络结构，降低语义和结构信息提取的复杂度.在语义关系建模方法中，虽然现有方法利用对称元路径简化异质网络结构，保留了丰富语义特征，但忽略了网络结构中关系语义信息的深度挖掘，无法充分发现不同连接关系和邻域节点语义提取的差异性，导致难以准确捕捉网络中的语义和结构特征，影响节点分类效果.

本文提出的方法充分利用了异质网络语义和结构信息，有效解决了异质网络节点分类问题.该方法可以深入挖掘语义关系特征，通过保留异质语义信息的关系表示向量和无1-sum约束的邻居节点权重充分发现不同连接关系和邻居语义提取的差异性，提升节点分类效果.

2 基于图卷积的异质网络节点分类框架(HNNCF)

本节重点介绍信息网络、异质网络、对称元路径、单节点多关系异质网络、语义化同质网络等概念及定义，并对HNNCF进行具体描述.

2.1 概念定义

定义1.信息网络.信息网络被定义为无向图G=(V,E,A,P,φ,φ)，其中，V表示节点集合，E表示关系集合，A表示节点类型集合，P表示关系类型集合，φ:V→A表示节点类型映射函数，φ:E→P表示关系类型映射函数.

异质网络是具有多种节点和关系类型的信息网络，多样化的节点和关系共同描述了异质网络中的语义信息，见定义2.

定义2.异质网络[15].给定信息网络Gh=(Vh,Eh,Ah,Ph,φh,φh)，如果|Ah|+|Ph|>2，则称Gh为异质信息网络，简称为异质网络.

例1.图1(a)所示的异质网络由多种类型的节点和关系构成，节点集合Vh={z1,s1,s2,s3,u1,u2}，关系集合Eh={〈z1,s1〉,〈z1,s2〉,〈z1,s3〉,〈s1,s2〉,〈s2,s3〉,〈s1,u1〉,〈s2,u1〉,〈s2,u2〉,〈s3,u2〉}，节点类型集合Ah={Z,S,U}，关系类型集合Ph={Z-S,S-S,S-U}，满足异质网络|Ah|+|Ph|>2的约束.其中：节点映射φh(z1)=Z，φh(s1)=φh(s2)=φh(s3)=S，φh(u1)=φh(u2)=U；关系映射函数φh(〈z1,s1〉)=φh(〈z1,s2〉)=φh(〈z1,s3〉)=Z-S，φh(〈s1,s2〉)=φh(〈s2,s3〉)=S-S，φh(〈s1,u1〉)=φh(〈s2,u1〉)=φh(〈s2,u2〉)=φh(〈s3,u2〉)=S-U.

元路径描述了异质网络上不同类型节点间的组合关系，而对称元路径是首尾对称的元路径，表达了同类型节点间的语义关系，详见定义3和定义4.

例2.在图1(a)所示的异质网络中，ZSU是1条长度为2的元路径，描述了节点类型Z,S,U之间的组合关系；SUS是1条长度为2的对称元路径，s1—u1—s2是对称元路径SUS的实例，表达了S类型节点s1，s2通过与u1节点相连构建的语义关系.

Fig. 1 Examples of different types of graph structures图1 不同类型的网络结构示例

单节点多关系异质网络由一种节点类型和多种关系类型构成，是异质网络的一个特例.该网络仅包含单一类型的节点，且节点之间具有多种类型的关系，详见定义5.

定义5.单节点多关系异质网络.给定信息网络Gr=(Vr,Er,Ar,Pr,φr,φr)，如果|Ar|=1且|Pr|>1，则称Gr为单节点多关系异质网络.此时，Er={〈vi,vj,t〉|vi,vj∈Vr∧t∈Pr}，即vi与vj间的任意关系均对应一种关系类型.

例3.如图1(b)所示，单节点多关系异质网络由一种节点类型和多种关系类型构成，节点集合Vr={s1,s2,s3}，关系集合Er={〈s1,s2,S-Z-S〉,〈s1,s2,S-U-S〉,〈s1,s2,S-S〉,〈s2,s3,S-Z-S〉,〈s2,s3,S-U-S〉,〈s2,s3,S-S〉,〈s1,s3,S-Z-S〉}，节点类型集合Ar={S}，关系类型集合Pr={S-Z-S,S-S,S-U-S}，满足单节点多关系异质网络|Ar|=1和|Pr|>1的约束.其中，节点映射函数φr(s1)=φr(s2)=φr(s3)=S，关系映射函数φr(〈s1,s2〉)=φr(〈s2,s3〉)={S-Z-S,S-S,S-U-S}，φr(〈s1,s3〉)={S-Z-S}.

与异质网络不同的是，语义化同质网络仅包含单一的节点类型和关系类型，同类型节点间的关系表示描述了关系包含的语义信息.

定义6.语义化同质网络.给定信息网络Gg=(Vg,Eg,Ag,Pg,φg,φg)，如果|Ag|=1且|Pg|=1，则称Gg为语义化同质网络，简称为同质网络.此时，Eg={〈vi,vj,ei,j〉|vi,vj∈Vg∧ei,j∈m}，Pg={tg}，vi与vj间仅具有唯一关系类型tg，且对应m维异质关系表示ei,j，表达了关系的异质语义信息.

例4.如图1(c)所示，语义化同质网络由一种类型的节点和关系构成，节点集合Vg={s1,s2,s3}，关系集合Eg={〈s1,s2,e1,2〉,〈s2,s3,e2,3〉,〈s1,s3,e1,3〉}，节点类型集合Ag={S}，关系类型集合Pg={tg}，满足语义化同质网络|Ag|=1和|Pg|=1的约束.其中，节点映射函数φg(s1)=φg(s2)=φg(s3)=S，关系映射函数φg(〈s1,s2〉)=φg(〈s2,s3〉)=φg(〈s1,s3〉)={tg}.

为了方便叙述，表1给出了HNNCF中用到的符号，并解释了符号代表的含义.

Table 1 Symbol Explanation Table表1 符号对照表

2.2 HNNCF框架描述

为了对异质网络上特定类型的节点进行分类，本文提出一种基于图卷积的异质网络节点分类框架(HNNCF)，学习异质网络上的语义关系和网络结构信息，提升节点类别标签识别的精准性.

异质网络的结构复杂、语义丰富，为了合理地学习异质网络中的语义特征，通常将异质网络转换成同质网络，然后利用图神经网络学习节点表示，但在转换同质网络的过程中，缺乏关系特征建模，难以有效利用语义关系信息.因此，HNNCF首先通过异质网络约简，将异质网络转换成语义化同质网络，简化网络结构并充分保留异质网络的多语义信息.

DGL(deep graph library)[18]，PyG(PyTorch geometric)[19]等主流图神经网络计算库使用的消息传递框架是一种图卷积网络泛化框架，支持节点特征、关系特征和邻域结构等特征信息建模[10].为了融入异质语义特征、充分利用关系特征和邻居权重等网络结构信息，HNNCF基于消息传递框架设计图卷积节点分类方法，学习合理的邻居节点权重，进一步生成节点异质语义表示，提升节点类别标签识别精度.

HNNCF主要包括2个阶段，分别是异质网络约简和图卷积节点分类，如图2所示.

1) 异质网络约简.给定待学习表示的节点类型，将异质网络简化为语义化同质网络，保留多种语义信息，便于适应消息传递框架.首先，利用对称元路径，将异质网络转换成单节点多关系异质网络，通过节点间不同的关系类型保存异质网络中的多种语义信息.然后，对节点间的多重关系进行语义融合，将单节点多关系异质网络进一步转换成语义化同质网络，利用节点间的关系表示向量保存融合后的异质语义信息.

2)
图卷积节点分类.基于消息传递框架和语义化同质网络，设计图卷积网络节点分类方法，融入异质语义信息和网络结构信息.首先，结合关系表示向量，学习邻居权重，区分邻居节点重要性，并对邻域特征进行加权聚合，生成节点异质语义表示.然后，利用全连接层将节点异质语义表示投影到类别空间，计算节点的类别概率分布，并根据类别概率分布确定节点的类别标签.

3 异质网络约简方法

本节详述HNNCF的异质网络约简方法，设计转换规则，将异质网络简化为语义化同质网络，利用节点间的关系表示保存异质网络中的多语义信息.

3.1 异质网络—单节点多关系异质网络转换

首先将异质网络Gh转换为单节点多关系异质网络Gr，受文献[15]启发，本文设计了转化规则进行网络结构初步化简，通过不同的对称元路径构建同类型节点间的多语义关系.

对于给定的特定节点类型Ac，令M为异质网络Gh上的对称元路径集合，即M={f=A1A2…Aδ+1|A1=Ac∧∀i∈[1,l+1]，Ai=Aδ+2-i}.下面给出从异质网络Gh=(Vh,Eh,Ah,Ph,φh,φh)到单节点多关系异质网络Gr=(Vr,Er,Ar,Pr,φr,φr)的网络结构转换规则.

规则1.节点转换规则.给定节点类型Ac，∀vi∈Vh，若φh(vi)=Ac⇒构建节点集合Vr={vi|vi∈Vh∧φh(vi)=Ac}.

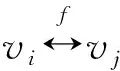
规则3.类型转换规则.构建节点类型集合Ar={Ac}；关系类型集合Pr={t|t=ω(f)∧f∈M}.

规则4.映射转换规则.令节点类型映射函数φr=φh；关系类型映射函数φr:Er→Pr，φr(vi,vj)={t|〈vi,vj,t〉∈Er∧vi,vj∈Vr∧t∈Pr}.

规则1转换后的节点集合Vr仅保留给定类型Ac的节点，且Vr⊂Vh.

规则2构建转换后的关系集合Er，如果Vr中的节点vi和vj在异质网络Gh上通过对称元路径f进行连接，则vi和vj之间在单节点多关系异质网络Gr中具有连接关系，对应的关系类型t可以保留化简前节点间的语义信息，vi和vj之间的连接关系可以有多种，且关系类型也不一定相同.ω为对称元路径集合M到关系类型集合Pr的映射函数，构建了对称元路径f与关系类型t之间的一一映射关系.

规则3转换后的节点类型集合Ar只有一种类型Ac，且Ar⊂Ah；规则4中节点类型映射函数保持不变，即φr=φh.与转换前的关系类型不同，规则3和规则4将生成新的关系类型，在异质网络Gh中节点类型为Ac的节点之间，如果存在不同的对称元路径，则分别对应单节点多关系异质网络Gr中不同的关系类型.

利用对称元路径进行网络结构转换，可以保留特定的节点类型，并构建节点间的多重语义关系，不仅降低了网络结构复杂度，而且保留了节点间的异质语义信息.

例5.如图1(a)和图1(b)所示，设Ac=S，M={S-Z-S,S-U-S,S-S}，根据异质网络—单节点多关系异质网络转换规则，可知Vr={s1,s2,s3}，Er={〈s1,s2,S-Z-S〉,〈s1,s2,S-U-S〉,〈s1,s2,S-S〉,〈s2,s3,S-Z-S〉,〈s2,s3,S-U-S〉,〈s2,s3,S-S〉,〈s1,s3,S-Z-S〉}，Ar={S}，Pr={S-Z-S,S-U-S,S-S}.其中，ω分别将元路径映射为S-Z-S，S-U-S，S-S类型.

3.2 单节点多关系异质网络—同质网络转换

由3.1节的网络结构转化规则，得到单节点多关系异质网络Gr.本节进一步讨论简化网络结构的方法，把Gr转换为语义化同质网络Gg，并将异质语义融入到Gg的关系表示中.

本文首先利用embedding方法[20]和Gr的关系类型集合Pr构建关系类型嵌入表T，对于每种关系类型t∈Pr，在T中设置对应的向量表示et∈m，通过向量形式表达关系类型的语义信息，m为关系类型表示的维度.

给定关系类型嵌入表T，通过规则5～8所示的关系语义转换规则将单节点多关系异质网络Gr=(Vr,Er,Ar,Pr,φr,φr)转换为语义化同质网络Gg=(Vg,Eg,Ag,Pg,φg,φg).

规则5.节点转换规则.构建节点集合Vg=Vr.

规则6.关系转换规则.构建关系集合Eg={〈vi,vj,ei,j〉|ei,j=Θt∈φr(vi,vj)et∧et∈T}.

规则7.类型转换规则.构建节点类型集合Ag=Ar，关系类型集合Pg={tg}.

规则8.映射转换规则.设置节点类型映射函数φg=φr，构建关系类型映射函数φg:Eg→Pg，φg(vi,vj)={tg|〈vi,vj,ei,j〉∈Eg∧tg∈Pg}.

由于转换前后节点未发生变化，规则5转换后的节点集合保持不变，保留了单节点多关系异质网络中Gr中的所有节点.

规则6转换后的关系类型集合Eg中，vi和vj间的多种关系类型φr(vi,vj)被max，add，mean等池化聚合函数Θ转换为单一关系类型tg，并将融合后的多种关系语义信息保存到异质关系表示ei,j中.

因为语义化同质网络Gg中只包含一种节点类型和关系类型，规则7转换后节点类型集合Ag仅包含一种节点类型Ac，Ag=Ar.同时，规则8会生成新的关系类型tg，转换为语义化同质网络Gg后，节点间的关系类型均相同.

通过关系语义转换规则，节点vi和节点vj间的多语义关系被转换成了具有异质关系表示ei,j的单一关系连接，不仅融合了多种异质语义信息，同时进一步将单节点多关系异质网络简化为了语义化同质网络，便于适应消息传递框架.

例6.如图1(b)和1(c)所示，通过为关系类型S-Z-S，S-U-S，S-S设置向量表示eS-Z-S，eS-U-S，eS-S，并根据单节点多关系异质网络—同质网络转换规则，可得Vg={s1,s2,s3}，Eg={〈s1,s2,e1,2〉,〈s2,s3,e2,3〉,〈s1,s3,e1,3〉}，Ag={S}，Pg={tg}.

4 图卷积节点分类方法

本节讨论HNNCF的图卷积节点分类方法.基于消息传递框架，设计消息传递过程，学习语义化同质网络上的邻居节点权重、语义关系、邻域上下文等网络结构特征，生成更新节点表示，并输入单层全连接层，计算节点的类别概率分布，识别类别标签.

4.1 消息传递过程

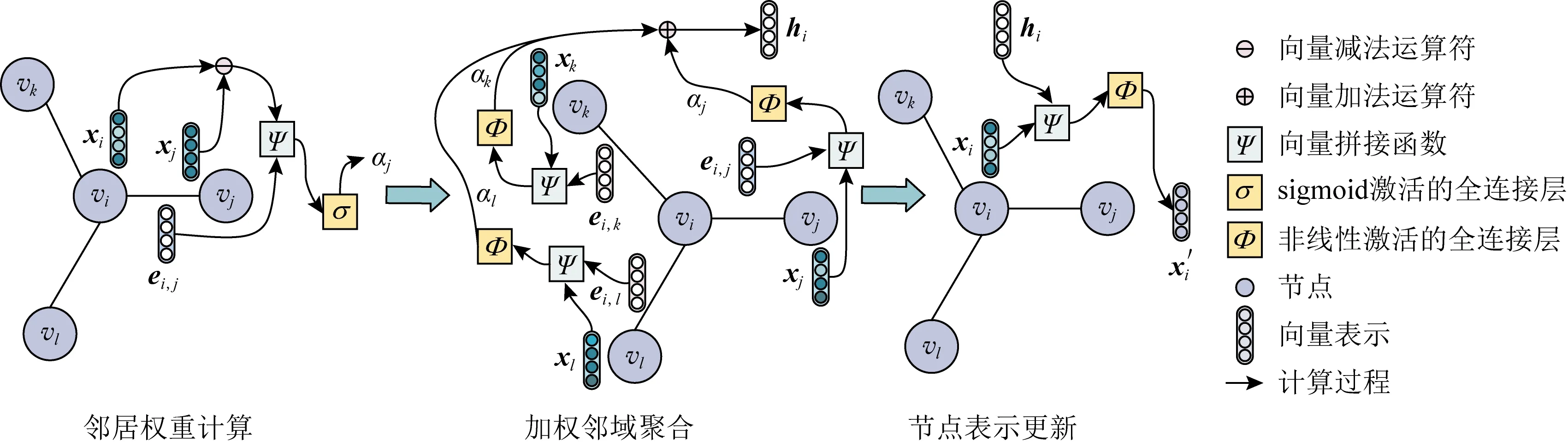
Fig. 3 The message passing process图3 消息传递过程

消息传递框架是一种图卷积泛化框架，能够灵活建模节点特征、关系特征和邻域特征，主要通过邻域特征聚合和节点表示更新实现图卷积操作[10]，分别如式(1)、式(2)所示：

(1)

(2)

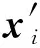
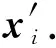
本文利用消息传递框架，学习语义化同质网络Gg中的节点表示，用于识别节点类别标签.给定节点初始特征表示集合X={xi∈n|vi∈Vr}，可从节点的文本、属性等内容中提取，或利用embedding方法[20]学习节点的初始特征表示.

图3展示了由中心节点vi及其邻居节点vj,vk,vl构成的语义化同质网络上的消息传递过程.其中，xi,xj,xk,xl分别为节点vi,vj,vk,vl的初始特征表示；ei,j,ei,k,ei,l分别为中心节点vi与邻居节点vj,vk,vl之间的异质关系表示.具体步骤为：

1) 邻居权重计算.以邻居节点vj为例，根据vi和vj的初始特征表示之差xi⊖xj，以及异质关系表示ei,j，计算邻居节点vj的邻居权重αj.

2) 加权邻域聚合.利用非线性变换提取邻居节点初始特征表示和异质关系表示中的特征，并通过邻居权重加权聚合，获取中心节点vi的邻域上下文表示hi.

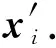
4.1.1 邻居权重计算

为了区分不同邻居节点的重要性程度，减少不相关邻居节点引入的噪声，本文借鉴注意力机制[12]和关系卷积[9]的思想，设计了具体的邻居权重计算方法.利用中心节点vi和邻居节点vj的特征表示之差xi⊖xj和异质关系表示ei,j，计算邻居节点vj的邻居权重αj，确定邻居节点的重要性，具体计算方法为

αj=σ((Wwgt·Ψ(xi⊖xj,ei,j))+bφr(vi,vj)),

(3)

其中，αj∈(0,1)为邻居节点vj相对于vi的权重，σ为sigmoid函数，Wwgt∈1×(n+m)是全连接层的权重，·为矩阵乘法运算符，⊖为向量减法运算符，+为标量加法运算符，Ψ为向量拼接函数.

同时，式(3)为每种关系类型组合学习特定的偏量bφr(vi,vj)∈1，以尽可能地区分中心节点vi和不同邻居节点vj之间的语义关系.其中，关系类型组合偏量的个数为2|T|-1，|T|表示关系类型的数目.设关系类型嵌入表T中包含2种关系类型t1和t2，则可能的关系类型组合为{{t1},{t2},{t1,t2}}.

与同质网络不同，异质网络约简后构建的邻居节点通常数量不一，相关性差异较大，需要区分不同邻居节点的重要性，以生成合理的节点表示.GAT[8]等图注意力机制在计算邻居权重时存在1-sum约束，需要利用softmax函数对邻居权重进行归一化，使所有权重之和为1.然而，1-sum约束对邻居节点数量敏感，使得邻居权重的确定产生偏向性，邻居节点数量较少时会使权重偏大，数量较多时会使权重偏小，导致邻居权重学习相对不合理.例如，当邻居节点数为100时，如果邻居节点均非常相关，1-sum约束会使得邻居权重约为0.01，过小的邻居权重会导致难以提取单个邻居节点的特征.同时，当邻居节点数为10，如果邻居节点均不相关，1-sum约束仍会使得邻居权重约为0.1，为不相关邻居节点设置了较大的权重，从而引入了噪声.

因此，本文去除了邻居节点权重的1-sum约束，通过sigmoid函数将权重限定在(0,1)内，权重之和不为1.同时，邻居节点权重的大小由初始特征表示之差xi⊖xj、异质关系表示ei,j、全连接层权重Wwgt和组合类型偏量bφr(vi,vj)共同确定，不需要使用softmax进行归一化，不受邻居节点数量的干扰，缓解了因邻居节点数量变化引起的偏向性问题.节点特征表示之差xi⊖xj、异质关系表示ei,j和组合类型偏量bφr(vi,vj)分别体现了初始特征分布和语义关系的不同，充分考虑了中心节点和邻居节点连接关系的差异性.

4.1.2 加权邻域聚合

在计算邻居权重之后，首先会对邻居节点vj的节点特征xj和异质关系表示ei,j进行非线性变换，然后利用邻居节点权重αj计算加权特征表示wj，并提取vi的邻域上下文表示hi，如式(4)和式(5)：

wj=αj×Φ((Wngb·Ψ(xj,ei,j))⊕bngb)，

(4)

(5)

式(4)和式(5)中，Ni表示中心节点vi的邻居节点集合，Φ是非线性激活函数，Wngb∈o×(n+m)和bngb∈o分别表示全连接层的权重和偏量，o表示邻域上下文表示的维度，·表示矩阵乘法运算符，×表示标量乘法运算符，⊕表示向量加法运算符，Ψ表示向量拼接函数.

加权邻域聚合综合考虑了邻居节点的特征和权重，以及中心节点vi与邻居节点vj之间的异质关系表示ei,j等多种网络结构信息，充分挖掘了连接关系和邻居节点语义提取的差异性，获得了更加合理的邻域特征，减少了邻域结构中的噪声.

此外，类似于GCN[3]，在进行加权邻域聚合时，本文使用度归一化平衡因不同节点度引起的尺度不一致问题，同时避免在邻居节点数目较多时和权重较大时可能产生的梯度爆炸问题.

本文将式(1)分为了邻居权重计算和加权邻域聚合2个步骤.首先，结合异质语义表示ei,j学习邻居节点权重αj，充分利用关系表示中的异质语义信息.然后，利用全连接层和非线性转换函数实现了消息传递函数F，根据不同邻居节点的重要性提取加权特征表示wj.最后，聚合邻域特征，生成中心节点vi的邻域上下文表示hi.

4.1.3 节点表示更新

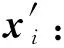
(6)

其中，Φ是非线性激活函数，Wupt∈d×(n+o)和bupt∈d表示全连接层的权重和偏量，d表示更新节点表示维度，·为矩阵乘法运算符，⊕表示向量加法运算符，Ψ为向量拼接函数.

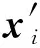
4.2 节点类别识别

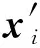
(7)

其中，Wcls∈d×K表示全连接层的权重，K表示节点类别标签数，·为矩阵乘法运算符.

对于类别标签向量Y=(y1,y2,…,yK)，根据类别概率分布Pi=(p1,p2,…,pK)，确定概率最大的分量对应的类别标签y作为中心节点vi最终的分类结果.

基于HNNCF设计异质网络节点分类算法，参见算法1.

算法1.异质网络节点分类算法.

输入：异质网络Gh=(Vh,Eh,Ah,Ph,φh,φh)、对称元路径集合M、待分类的节点类型Ac、节点初始特征表示集合X；

输出：节点类别标签集合L.

①L=∅；/*初始化类别标签集合,将异质网络约简为语义化同质网络*/

②Gg=Reduce(Gh,M,Ac)；

③ forviinVgdo/*迭代处理每个中心节点,获取vi的邻居节点集合Ni*/

④Ni=GetNeighbors(vi,Eg);

⑤ forvjinNido/*迭代处理每个邻居节

点,计算邻居节点vj的权重系数αj*/

⑥αj=σ((Wwgt·Ψ(xi⊖xj,ei,j))+

bφr(vi,vj));/*计算邻居节点vj的加

权特征表示wj*/

⑦wj=αj×Φ((Wngb·Ψ(xj,ei,j))⊕bngb);

⑧ end for/*终止内层循环,计算中心节点vi的邻域上下文表示hi*/

表示更新中心节点表示*/

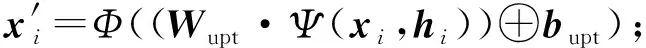
率分布*/

/*获取类别标签*/

/*将vi的类别标签加入L中*/

具体地，算法1的行①②表示初始化类别标签集合L，并利用第3节异质网络约简方法，将异质网络Gh转换成同质网络Gg.行③～表示迭代地计算每个节点vi∈Vr的类别标签y的过程.行行返回算法的计算结果.

其中，行④表示利用函数GetNeighbors和关系集合Eg获取vi的邻居节点集合.行⑤～⑧表示计算邻居节点vj的权重αj和加权特征表示wj.

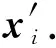
假设|N|表示Vr中节点的平均邻居数，根据HNNCF的计算步骤，时间复杂度可表示为O(m×|Vr|×|M|×|N|+o×(m+n)×|Vr|×|N|+d×(n+o)×|Vr|)，|Vr|，|M|分别表示节点集合Vr和对称元路径集合M的大小.当网络规模较大时，可以重写为O(|Vr|×|N|)，即时间复杂度主要受Gr的节点数和平均邻居数影响.

HNNCF的空间复杂度可表示为O(n×|Vr|+|Er|+m×|M|+o×(n+m)+d×(n+o))，当网络规模较大时，空间复杂度可以重写为O(n×|Vr|+|Er|)，即空间复杂度主要受Gr中节点的初始特征表示维度、节点数和关系数影响.

5 实验及效果评估

5.1 实验数据

为了评估所提方法HNNCF的有效性，本文使用文献[15]公开发布的3个异质网络节点分类数据集ACM,DBLP,IMDB进行了实验.数据集的具体说明如表2所示：

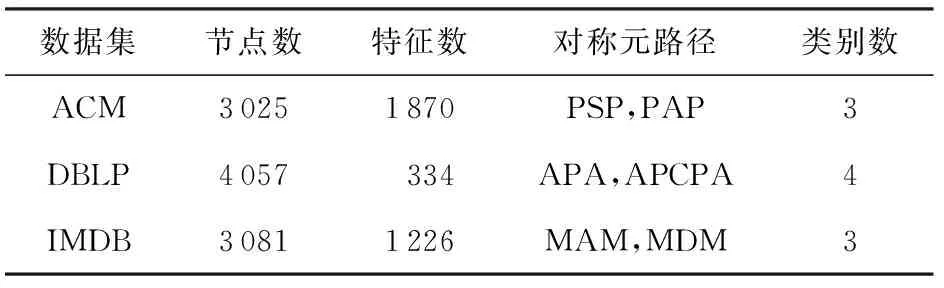
Table 2 Statistics of Node Classification Datasets表2 节点分类数据集的统计信息

对于DBLP数据集，由于元路径APTPA包含的语义信息较少，本文仅使用元路径APA和APCPA进行实验.同时，对于IMDB数据集，因为只能获得未经处理的原始数据，本文根据文献[15]的方法进行处理，生成实验数据.

本文按4∶2∶4的比例将每个数据集划分为训练集、验证集和测试集.其中，训练集用于训练模型，验证集用于验证模型训练效果，测试集用于评估模型性能.采用macro-F1[21]和balanced accuracy[22]作为评价指标，用于评估节点分类的综合性能和类别不平衡情况下的学习效果.

5.2 对比方法

为了验证HNNCF的有效性，实验选取了5种同质和异质图神经网络进行对比：

1) GCN[3].同质图神经网络，对邻居节点的特征表示进行均值池化学习节点特征表示.

2) GraphSAGE[7].同质图神经网络，对邻域进行采样，并聚合采样邻域的特征.本实验仅使用1-hop邻居，并采用mean作为聚合运算符.

3) GAT[8].同质图神经网络，在一阶局部子图上执行注意力机制，并为中心节点邻域中的不同邻居指定不同的权重.

4) HAN[15].基于GAT的异质图神经网络，通过节点级和语义级的注意力方式，聚合邻居节点的特征来生成节点表示.

5) CompGCN[17].异质图神经网络，通过关系类型组合算子对多关系网络进行建模，并结合节点和关系特征表示聚合邻域的语义特征.

HNNCF是本文所提的基于图卷积的异质网络节点分类方法的具体实现框架.同时，为了评估1-sum约束对节点表示学习的影响，本文使用HNNCF+1-sum表示去除度归一化并添加邻居权重1-sum约束后的方法.为了评估异质网络多语义信息的有效性，使用HNNCF-mult表示仅使用单条元路径约简，执行HNNCF所得到的最优结果.此外，本文使用HNNCF-wght表示不对邻居节点进行区分、将邻居权重均设为1的方法，用于评估邻居权重学习的重要性.

实验基于PyTorch和PyG，实现了HNNCF和其他对比方法，并利用Cross Entropy[21]和Adam[23]优化模型参数.为了进行公平比较，实验为所有中心节点添加自环以保留中心节点特征信息，并统一设置更新节点表示维度d=64，训练批量大小为16.

与文献[15]相同，对于GCN,GraphSAGE,GAT,HNNCF-mult方法，本实验对所有元路径的性能进行测试，并展示最优结果.对于CompGCN和HNNCF方法，在ACM数据集上，由于通过对称元路径PSP查找到的邻居过多造成网络退化，本实验对基于PSP的邻居节点进行采样，使其邻居数与对称元路径PAP相同.

同时，实验测试了学习率为0.000 1,0.000 5,0.001,0.005,0.01的情况，并使用容忍度为20轮的提前终止策略[21]防止模型过拟合.由于模型参数的随机初始化和提前终止会对最终结果造成一定影响，本文采用每个方法在每个数据集上运行10次，取计算结果平均值.

5.3 实验结果

表3和表4分别展示了不同图神经网络方法在ACM,DBLP,IMDB数据集上的macro-F1和balanced accuracy值.

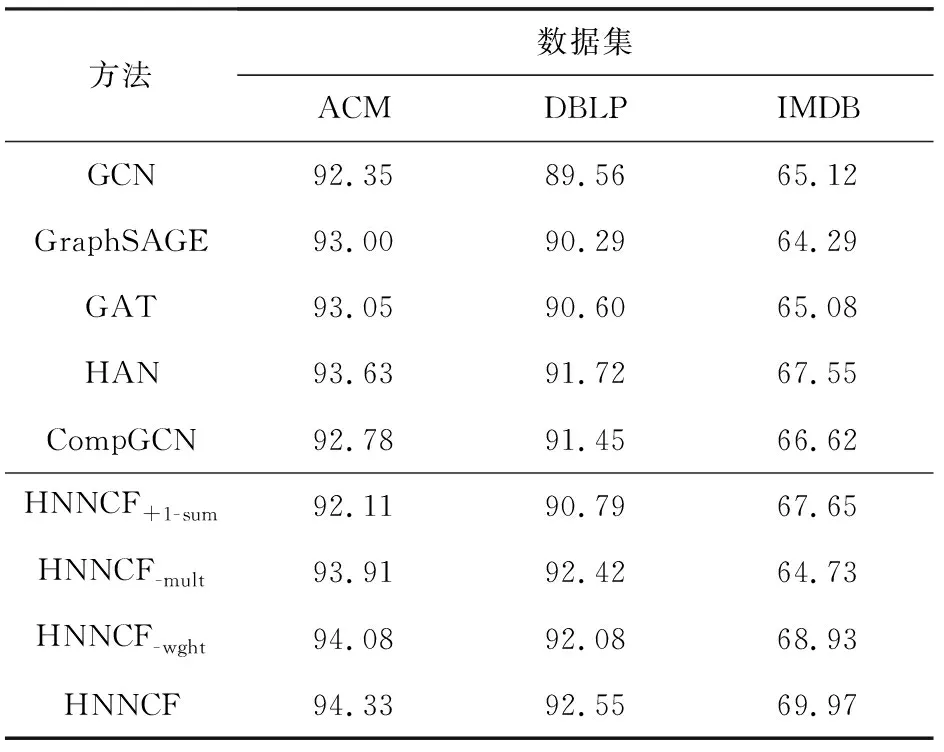
Table 3 Comparison of macro-F1 for Different Methods表3 不同方法在macro-F1上的对比 %

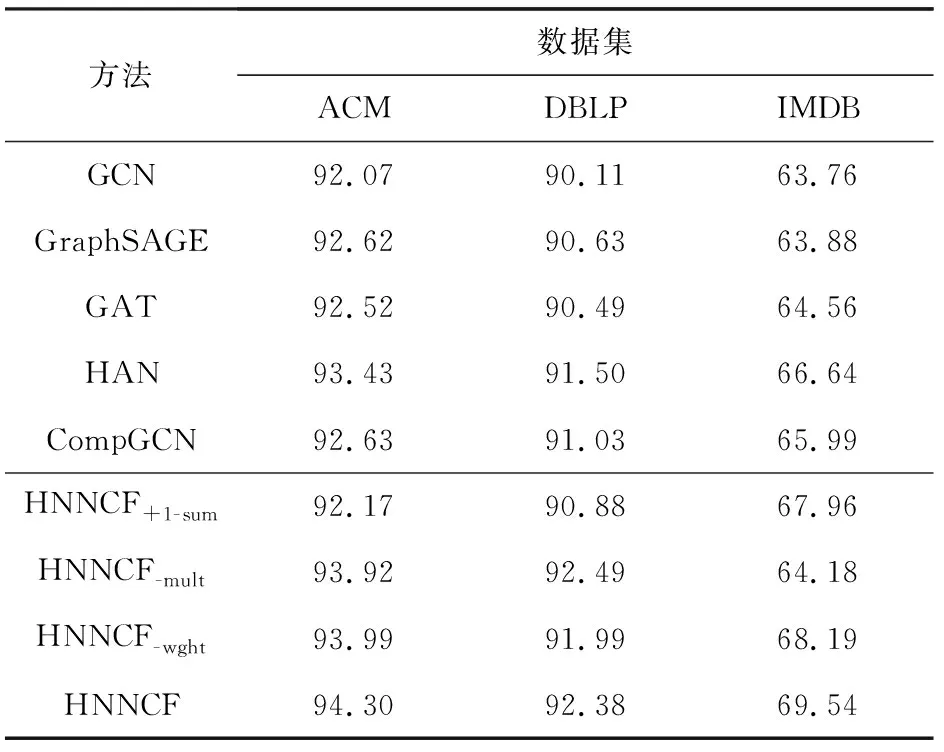
Table 4 Comparison of balanced accuracy for Different Methods表4 不同方法在balanced accuracy上的对比 %

从表3和表4可以得出4点结论：

1) HNNCF在3个节点分类数据集上取得了最佳性能，验证了本文所提方法的有效性.具体地，在IMDB数据集上，HNNCF的性能大大优于对比方法，分别在macro-F1和balanced accuracy上提高了2.42%～5.68%和2.9%～5.78%.同时，对于ACM和DBLP数据集，HNNCF在maro-F1上分别提高了0.7%～1.98%和0.83%～2.99%，在balanced accuracy上分别提升了0.87%～2.23%和0.88%～2.27%.

2) 异质图神经网络方法的性能比同质图神经网络方法更好(CompGCN在ACM数据集上的macro-F1性能除外)，表明异质图神经网络具有更强大的语义表达能力，能够学习更加丰富的异质语义特征，提升节点分类效果.特别地，HNNCF的maroc-F1值在ACM数据集上比同质图神经网络高1.28%～1.98%，在DBLP数据集上高1.95%～2.99%，在IMDB数据集上高4.58%～5.68%.同时，HNNCF的balanced accuracy值在ACM数据集上的提升幅度为1.68%～2.23%，在DBLP数据集上为1.75%～2.27%，在IMDB数据集上为4.98%～5.78%.此外，分析实验数据发现，同质图神经网络方法GCN，GraphSAGE，GAT，HNNCF-mult在ACM，DBLP，IMDB数据集上的最优对称元路径均相同，分别为PAP，APCPA，MAM，说明对称元路径的选取是影响节点分类效果的主要因素，但是各方法的实验结果存在较大差异，说明不同方法也会对分类效果造成一定影响.

3) HNNCF的结果优于HNNCF+1-sum方法，表明去除1-sum约束有利于提升HNNCF的节点分类效果.由实验结果可知，添加1-sum约束后，HNNCF在ACM，DBLP，IMDB上的macro-F1值分别下降了2.22%，1.76%，2.32%，balanced accuracy值分别下降了2.13%，1.5%，1.58%.同时，实验分析发现，去除1-sum约束有利于增大邻居权重和节点表示每个特征维度的方差，从而增加节点的区分能力.

4) HNNCF的性能要优于HNNCF-mult和HNNCF-wght，表明HNNCF可以通过异质语义融合和邻居权重学习获得更好的节点表示.仅使用一条对称元路径后，HNNCF-mult无法获取异质语义信息，导致在ACM，DBLP，IMDB数据集上的macro-F1值分别下降了0.42%，0.13%，5.24%，在ACM和IMDB数据集上的balanced accuracy值分别下降了0.38%和5.36%.从HNNCF-wght的macro-F1值可以看出，学习邻居节点权重对ACM和DBLP数据集有轻微影响，分别增加了0.25%和0.47%.同时，不学习邻居节点权重会对IMDB数据集产生较大影响，macro-F1降低了1.04%，balanced accuracy降低了1.35%.

为了直观地展示HNNCF所学节点表示的有效性，本实验利用t-SNE[24]方法对不同方法在DBLP数据集上学习的节点表示进行降维，得到2维可视化结果如图4所示.注意，由于t-SNE方法在降维时选择的坐标轴不同，可视化结果中节点类别的相对位置发生了改变，但并不影响结果的分析.

Fig. 4 Visualization on the DBLP dataset图4 DBLP数据集上的节点表示可视化

由图4可知，与同质图神经网络方法相比，异质图神经网络方法可以学习更好的节点表示.GCN,GraphSAGE,GAT仅考虑异质网络中的单一语义，会使得节点的每个类别都包含多个呈团状或条纹状的簇，导致决策边界不平滑，从而干扰节点类别的预测.在异质图神经网络中，相比于HAN,HNNCF，CompGCN未考虑邻居节点的重要性，不能有效区分邻居类型，虽然可以将相同类别的节点聚在一起，但是仍然存在相对分散的情况，从而导致错误的识别结果.HAN和HNNCF均可以将节点聚成4个几乎完全分离的、在空间中分布良好的簇，因为相同类型的节点集中在特定区域，决策边界更加平滑，从而使得分类结果更好.但与HAN不同，HNNCF消除了邻居权重的1-sum约束，并利用了多种语义关系特征，移除了部分邻域噪声，减少了节点类别的重叠.

5.4 参数分析

为了评估模型参数的影响，本文对学习率rlearn、关系表示维度m、邻域上下文表示维度o和更新节点表示维度d进行了参数敏感性分析，结果如图5所示:

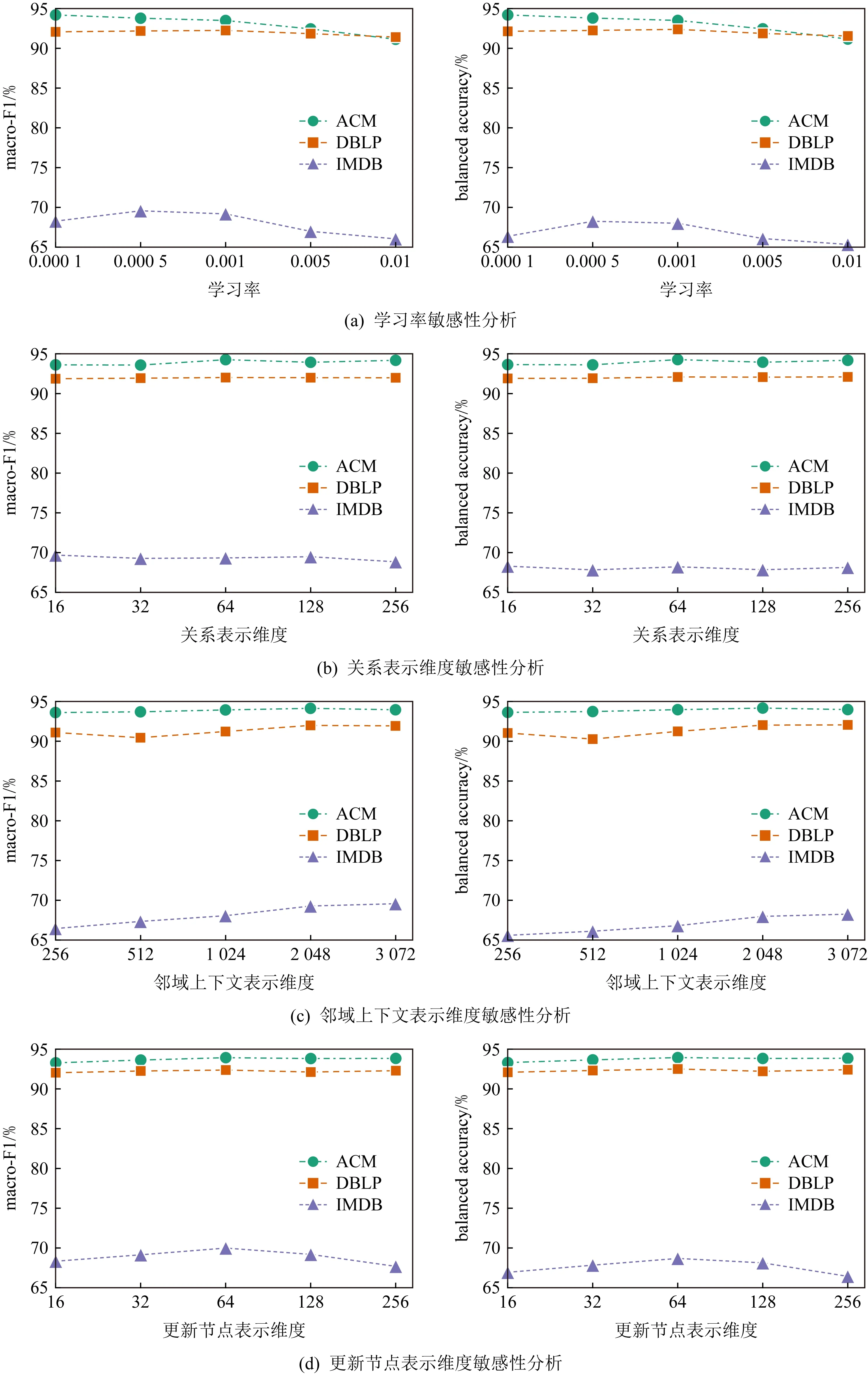
Fig. 5 Parameter sensitivity analysis图5 参数敏感性分析

由图5可知：

1) 学习率对HNNCF有着较大的影响，大的学习率会导致HNNCF的性能显著下降.在学习率较小时，增加学习率会略微降低ACM数据集上的性能、略微提升DBLP和IMDB数据集上的性能，而随着学习率的继续增大，HNNCF在3个数据集上的macro-F1值和balanced accuracy值均出现明显的下降趋势，说明学习率会影响HNNCF的训练过程和学习效果，学习率较大时会造成HNNCF训练效果变差，且不同数据的最佳学习率存在差异.因此，需要仔细调整学习率，以获得最优的节点分类结果.

Fig. 6 Statistics of edge pooling operators and neighbor weights图6 边池化运算符和邻居权重的统计信息

2) 关系表示维度m对HNNCF的影响较小.随着关系表示维度的增大，HNNCF在DBLP数据上的性能未发生较大变化；在IMDB数据集上的性能会产生细微幅度的波动；而在ACM数据集上的macro-F1值和balanced accuracy值会略微增加，而后基本保持不变.由表2可知，3个数据集均包含2条对称元路径，在异质网络约简过程中，均会产生2种关系类型，并学习对应的关系向量表示.在关系表示维度m较小时，增加m有利于区分2种不同的关系类型，从而略微提升HNNCF在ACM数据集上的分类效果.但随着m的增加，对关系类型的区分能力基本保持不变，使得HNNCF对m变得不敏感，导致性能变化较小.因此，在保证足以区分不同关系类型的情况下，关系表示维度m的变化对HNNCF的结果影响较小.

3) 增加邻域上下文表示维度o可以改善HNNCF的节点分类效果.随着o的增大，ACM,DBLP,IMDB数据集的macro-F1值和balanced accuracy值总体上均获得了提升.HNNCF在提取邻域上下文表示时，需要加权聚合邻居节点特征，增加o的大小可以提升HNNCF的模型容量，从而学习更多的邻域特征，增强最终的节点分类效果.因此，可以将邻域上下文表示维度设置为相对较大的值，以确保HNNCF达到较好的识别效果.

4) 更新节点表示维度d会对HNNCF造成一定影响.d的增大对DBLP数据集的影响不大，但是会略微提升HNNCF在ACM数据集上的性能，并造成IMDB数据集上性能的大幅变化.邻域上下文表示和节点初始特征表示是节点表示更新的主要依据，d的变化会导致HNNCF提取不同的特征，进而影响更新节点表示的质量.因此，需要仔细调整d，d过大或过小均会影响节点分类效果.

5.5 实例分析

为了进一步分析关系表示池化运算符的影响和邻居节点权重学习的效果，本文分别在ACM,DBLP,IMDB数据集上运行10次HNNCF方法，并对关系表示池化运算符max,add,mean的macro-F1值以及按“邻居节点是否与中心节点具有相同的类别”分类的邻居节点权重进行了数据统计，如图6所示：

如图6(a)所示，不同的关系表示池化运算符对HNNCF的分类效果有着较大的影响.在ACM数据集上，max运算符的表现最差，4分位间距分布在较大的区间内，性能相对不稳定；而与mean运算符相比，add运算符取得了更好的均值和最大值，但也会产生更差的最小值.在DBLP数据集上，add运算符虽然能取得最好的最大值，但是4分位间距分布更大，稳定性不如max和mean运算符.在IMDB数据集上，add运算符和mean运算符的结果相差不大，均比max运算符表现更好.注意，本文在训练过程中使用了提前终止防止过拟合，且模型参数是随机初始化的，所以在训练不充分的情况下会产生较差的意外结果，导致max,add,mean的统计结果中出现离群值.

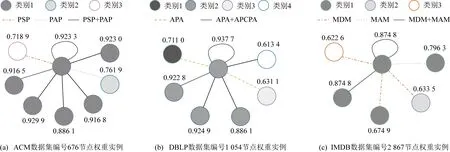
Fig. 7 Examples of neighbor weight learning图7 邻居权重学习实例

max运算符倾向于提取最重要的语义关系特征，弱化了相邻节点间不同关系类型组合的差异性，更适用于以某一关系类型为主的单节点多关系异质网络.而add运算符和mean运算符综合考虑了关系类型组合中所有的关系类型，在关系类型信息表达能力相差不明显的情况下，性能相对更加鲁棒.其中，mean运算符会对所有关系类型表示取平均，移除了关系类型数的影响，而add运算符通过直接加和的数值累计保留了关系类型数特征，有利于提升方法的最优性能，但也更易受到关系类型数的影响，多个关系类型表示加和可能会使池化后的异质关系表示在向量空间中发生较大偏移，进而产生较差的节点分类结果.

因此，不同的异质语义融合方式会造成HNNCF分类性能上的差异，应该仔细选择关系表示池化运算符，以使HNNCF达到最好的分类效果.

从图6(b)中可以看出，在3个数据集上，相同类别邻居节点的最大值、中位数和最小值均大于不同类别邻居节点，说明HNNCF可以为相同类别的邻居节点学习较高的权重，从而区分不同类型邻居节点的重要性程度，有利于减轻不重要的邻居节点引入的噪声，使得生成的节点表示更加合理.

为了进一步说明邻居节点权重的学习情况，我们分别在ACM,DBLP,IMDB数据集中提取了以节点676、节点1 054和节点2 867为中心节点的单节点多关系异质网络.如图7所示，不同图例的节点表示不同的类别，不同图例的线表示中心节点与邻居节点之间的不同连接关系，不同数字表示不同节点对应的邻居节点权重.

从图7可以看出，具有相同类别的邻居节点通常能够学习更高的权重，而与中心节点类别不同的邻居节点权重更低，与图6(b)的数据相符合.节点的初始特征表示包含了先验的类别信息，HNNCF在学习邻居权重时利用初始特征表示之差xi⊖xj作为特征，引入了节点初始特征表示的差异性，相同类别节点间的初始特征表示相对更小，从而提升了HNNCF的节点区分能力，使邻居权重学习更加合理.

此外，即使邻居节点与中心节点的类别相同，不同类型的连接关系也会导致不同的邻居权重.因为HNNCF在学习邻居权重时考虑了节点间的异质关系表示ei,j，表达了中心节点与邻居节点间的语义关系特征，使得不同连接关系在异质网络约简后的异质关系表示不同，进而影响邻居节点权重的确定.

因此，HNNCF可以通过学习合理的邻居节点权重，确定邻居节点的重要性，生成更加合理的节点表示.

6 总 结

本文提出了一种基于图卷积的异质网络节点分类框架(HNNCF)，利用转换规则将异质网络约简为语义化同质网络，并基于消息传递框架设计图卷积节点分类方法，解决了异质网络上的节点分类问题.不仅简化了异质网络结构，保留了多种语义信息，而且充分利用了网络结构信息，提升了节点分类性能.在3个公开的异质网络节点分类数据集上验证了本文所提方法的有效性.未来的研究将扩展HNNCF到链接预测、节点聚类等下游任务中，以适应更多的异质网络分析与挖掘场景.

作者贡献声明：谢小杰负责文章方法的设计与实验实现,以及文章整体架构设计、撰写和修改;梁英负责文章结构的设计与指导,以及文章撰写、修改和校对;王梓森负责部分实验实现、整理和分析，以及文章修改和校对；刘政君负责数据整理和校对.