一种毫米波雷达机场跑道异物检测算法

汤双霞

(广州番禺职业技术学院信息工程学院,广东 广州 511483)

1 引 言

机场跑道异物又被称为跑道外来侵入物(Foreign Object Debris,FOD),指的是出现在机场跑道上可能对航空器造成危害的一切物体,例如遗落在跑道上的扳手、硬币、电池、金属条等。FOD的存在严重威胁着飞机和旅客生命财产安全,2000年7月发生的协和客机空难事件正是由跑道上的金属长条引起,因此在飞机起飞和降落之前必须对跑道进行巡查,及时清除FOD。传统基于人工巡检的方式存在耗时长,效率低和可靠性差等问题,国内外相关领域研究机构和公司纷纷推出了各自的FOD自动检测系统,例如英国奎奈蒂克公司的Tarsier系统,新加坡策技系统公司的iFeeret系统,美国TrexEnterprises公司的FODFinder系统,以及北京大兴国际机场引进的以色列Xsight公司的FODetect系统。除IFeeret只采用光学传感器外,其余系统均采用毫米波雷达和光学传感器集成的处理体制以提升检测性能。由于光学传感器的检测性能受光照,天气等因素影响较大,而毫米波雷达具备全天时,全天候,高分辨率,对雨雪雾霾天气适应性强等优势,基于毫米波雷达的FOD检测成为了当前的研究热点[1-2]。

复杂机场跑道背景下实现对静止小目标的检测是毫米波雷达FOD检测系统面临的主要挑战[3],目前常用的是以单元平均恒虚警(Cell Averaging Constant False Alarm Rate,CA-CFAR)和排序类恒虚警(Order-Statistics Constant False Alarm Rate,OS-CFAR)为代表的空域CFAR方法,以及以杂波图恒虚警(Clutter Map Constant False Alarm Rate,CM-CFAR)为代表的时域CFAR方法。空域CFAR类方法认为杂波在空间的分布特性是连续的,通过对待测单元周边单元的杂波功率进行平均得到待测单元处的检测门限从而实现FOD检测,当杂波分布均匀时可以获得较好的检测性能,但是当杂波分布特性复杂,该类方法的检测性能出现明显下降[4-5]；时域CFAR方法通过对待测单元连续几次扫描得到信号功率进行平均作为检测门限,适用于杂波分布特性较为复杂的场景,但是当干扰信号存在时,该类方法会出现“自屏蔽”问题,从而导致虚警率升高[6]。为了解决上述问题,文献[7]提出一种结合CM-CFAR和模式分类的FOD分层检测方法,首先利用CM-CFAR进行杂波抑制,然后提取特征对FOD和虚警进行区分,虽然能够提升CM-CFAR的检测性能,但是存在运算复杂,计算效率低等问题；文献[8]首先利用CA-CFAR对跑道杂波进行抑制,然后提出一种基于粒子群-支撑向量数据描述(Particle Swarm Optimization Support Vector Domain Description,PSO-SVDD)一类分类器的FOD检测方法,利用PSO-SVDD对提取的功率谱特征进行分类,相对于CM-CFAR方法具备更高的检测概率,但是功率谱特征提取过程会造成回波中有用信息的丢失,同时其虚警率受制于CA-CFAR的性能。

在上述研究的基础上,提出一种基于双谱特征和SVDD的毫米波雷达FOD检测算法,首先利用双谱变换将接收到的信号转换至双谱域,然后提取双谱熵和二阶统计量二维特征构成特征向量对FOD和杂波信号进行区分,相对于功率谱特征,双谱特征保留了更多的相位信息,对不同目标具备更强的可分性,最后利用遗传模拟退火算法(Genetic Simulated Annealing Algorithm,GSAA)优化的SVDD一类分类器在特征域实现FOD检测。

2 FOD回波模型

线性调频连续波(Linear Frequency Modulated Continuous Wave,LFMCW)体制雷达由于具备高距离分辨率,硬件和软件复杂度低,低功耗,低成本以及无距离盲区等优势被广泛应用在FOD检测中,在一个扫频周期内,雷达发射的锯齿LFMCW信号可以表示为[9-10]:

(1)

其中,A和fo分别为发射信号的幅度和中心频率;u=B/T为调频斜率;B和T分别为扫频带宽和扫频周期。对于出现在跑道上距离雷达为R的静止FOD,其回波信号可以表示为:

(2)

其中,Ka为回波的幅度系数;τ=2R/c为双程距离引起的回波时延,将其代入式(2),并经过与发射信号(式(1))混频滤波后,可以得到差频信号如下所示:

(3)

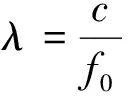
(4)

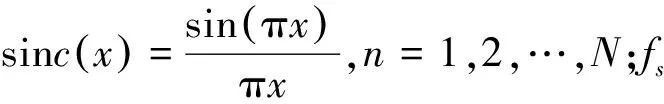
3 基于双谱特征和SVDD的FOD检测算法

图1给出了本文基于双谱特征和SVDD的FOD检测算法流程图,可以看出算法从上到下可以分为训练和测试两个阶段。在训练阶段,将雷达录取的机场跑道杂波实测数据作为训练数据集,然后利用双谱变换对其分析并提取双谱熵和二阶累计量二维特征构成特征向量,利用训练数据集的特征向量对SVDD分类器进行训练,同时针对SVDD核参数和惩罚因子选取问题,利用GSAA算法在全参数空间内进行寻优,最终获得最优SVDD分类面。

在测试阶段,将雷达录取的杂波或FOD回波信号作为测试数据集,同样利用双谱变换将其转换至差异性更大的双谱域,然后提取二维特征构成特征向量,最后利用训练阶段获得的最优分类面对特征向量进行分类判决,并最终给出该样本是FOD还是杂波的判决结果。

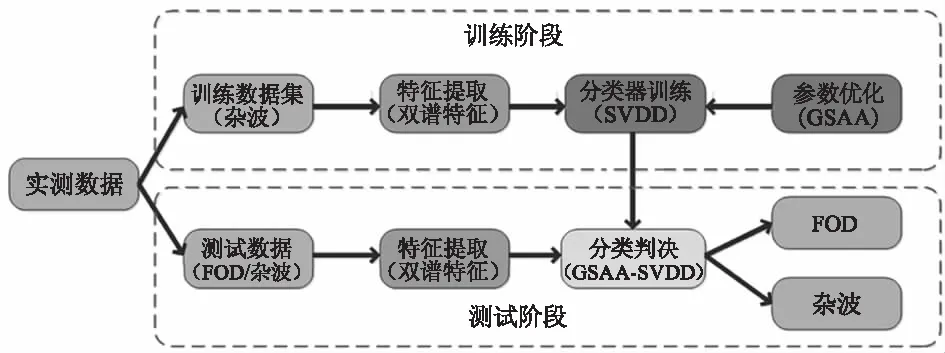
图1 本文算法流程图

3.1 双谱特征提取

在模式分类领域,原始数据维数较高且通常不能直接反映分类对象的本质属性,直接将其作为特征向量进行分类判决存在运算复杂、分类器设计困难等问题。特征提取通过对原始数据进行分析,从中综合出能够反映目标本质特性的信息,实现高维数据向低维空间的映射从而降低后续分类判决过程的复杂度[11]。传统功率谱特征丢掉了回波中的所有相位信息,使FOD和杂波信号趋同性增加,不利于目标分类,而双谱特征保留了回波中除线性相位外的所有相位信息,并且具备平移、旋转和尺度不变性,因此适合用于实现FOD和杂波的有效区分。

对于差频信号Sb(n),对其进行双谱变换的过程可以表示为[12]:

(5)

从式(5)可以看出双谱变换不但没有对差频信号降维,反而大大增加了信号维度,因此本文提取下述两维特征来描述双谱的分布特性。

特征1.双谱熵特征:

(6)

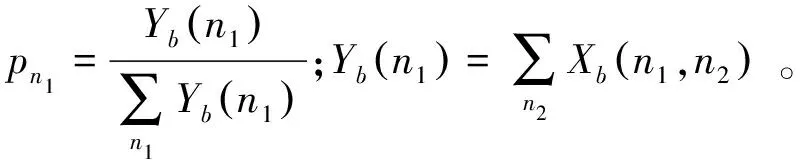
特征2.双谱二阶累计量特征:

(7)

3.2 SVDD一类分类器

出现在机场跑道上的FOD种类繁多且出现时机较为随机,通常难以获得足够多的FOD样本作为训练数据集,而机场环境(跑道,建筑物)较为稳定,短时间内不会发生变化,可以采集得到足够多的杂波样本用于训练,因此本文选用SVDD一类分类器实现FOD检测。SVDD是异常检测中应用比较广泛的一种一类分类器,只需要目标类样本即可构造闭合覆盖模型实现对未知测试样本的分类判决[13]。

(8)

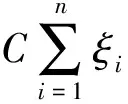
K(xi,xj)=(Φ(xi)·Φ(xj))

(9)

其中,Φ(xi)表示将xi映射到高维空间的映射函数;(Φ(xi)·Φ(xj))表示Φ(xi)和Φ(xj)的内积;δ为核参数,其大小决定着超球体边界的紧密性。通过引入拉格朗日乘子可以将式(8)转化为如下对偶形式:

(10)

其中,αi为与xi一一对应的模型参数,若αi>0,则其对应的xi为支撑向量。利用αi和对应xi可以计算得到最优超球体的球心和半径:

(11)

得到最优超球面后,对于任意未知测试样本x*,利用SVDD进行分类判决的决策方程为:

f(x*)=‖Φ(xi)-Φ(c)‖2-r2

(12)

若f(x*)≤0表明x*位于最优超球面内,x*为目标类样本,否则x*为异常样本。

3.3 基于GSAA的SVDD参数优化

SVDD分类性能受核参数s和惩罚因子C影响较大,目前常用的网格搜索法存在运算量大,实时性差的问题。本文将模拟退火(Simulated Annealing,SA)模型[14]引入遗传算法(Genetic Algorithm,GA)[15],将GA全局搜索能力强,局部搜索能力弱的特点和SA局部搜索能力强,全局搜索能力弱的特点进行优势互补,提出一种遗传模拟退火算法(Genetic Simulated Annealing Algorithm,GSAA)优化算法实现对SVDD核参数s和惩罚因子C全局寻优的同时最小化算法错分率,如式(13)所示:

(13)

其中,FP为漏警率,即FOD被判决为杂波的概率;FN为虚警率,即杂波被判决为FOD的概率。利用GSAA对SVDD进行优化的流程如图2所示,其基本思想是首先利用GA进行全局搜索,将当前条件下得到的最优解作为SA的初始值,然后利用SA进行局部搜索,并将获得的满足Metropolis准则的解作为下一轮迭代中GA的初始种群,依次往复迭代,全局搜索和局部搜索交替进行,直至满足终止条件。

图2 GSA-SVDD算法流程图

4 试验结果及分析

为了验证所提方法在真实场景下的FOD检测性能,在某地民用机场采用毫米波雷达录取实际数据开展试验。试验所用毫米波雷达工作在W波段,N=1024,中心频率f0=77 GHz,调频带宽B=600 MHz,扫频周期T=1 ms,中频采样频率fs=2 MHz,FFT点数,天线采用机械转动的方式实现对前方-60°～+60°空域的扫描,扫描速度为15°/s。

试验开始前首先对跑道进行人工巡查,确保跑道上没有FOD,然后利用毫米波雷达对跑道进行扫描并记录杂波数据作为训练样本,用于实现对SVDD分类器的训练。在测试阶段,构建两种试验场景:场景1中,在距离雷达40 m处放置一块体积为40 mm×40 mm×40 mm的砖块；场景2中,在距离雷达40 m和60 m处分别放置一个高尔夫球(直径43 mm)和场景1中的砖块。

图3(a)和图3(b)分别给出了两种测试场景中实测数据的轴向积分双谱图,其中实曲线对应FOD回波信号,虚曲线对应杂波信号。从图3可以看出在双谱域,FOD信号和杂波信号的分布特性呈现出明显差异,其中FOD的存在导致FOD回波信号的双谱波形波动性更大,而杂波信号的双谱波形更加平缓,可以据此实现两种目标的有效区分。

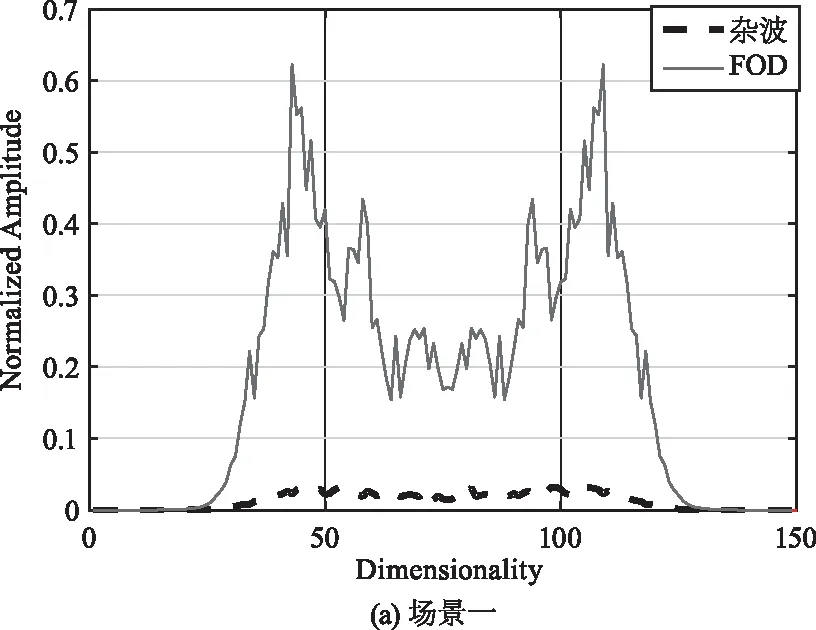
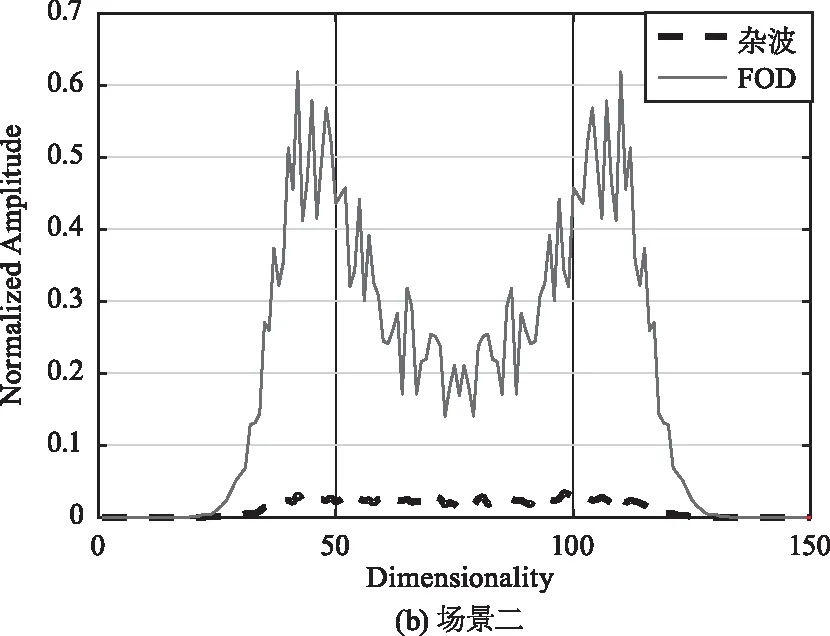
图3 轴向积分双谱

得到特征向量后,根据图1所示算法流程,需要利用GSAA算法对SVDD核参数和惩罚因子进行全局寻优,迭代开始时设置核参数s的初始值为1,取值范围为[0,10],惩罚因子C的初始值为0.1,取值范围为[0,1],最大迭代次数为100。图4给出了算法迭代过程中式(13)所示错分率的变化曲线,可以看出经过14次迭代,错分率曲线达到最小值,此时对应的最优核参数s=5.7,惩罚因子C=0.25。

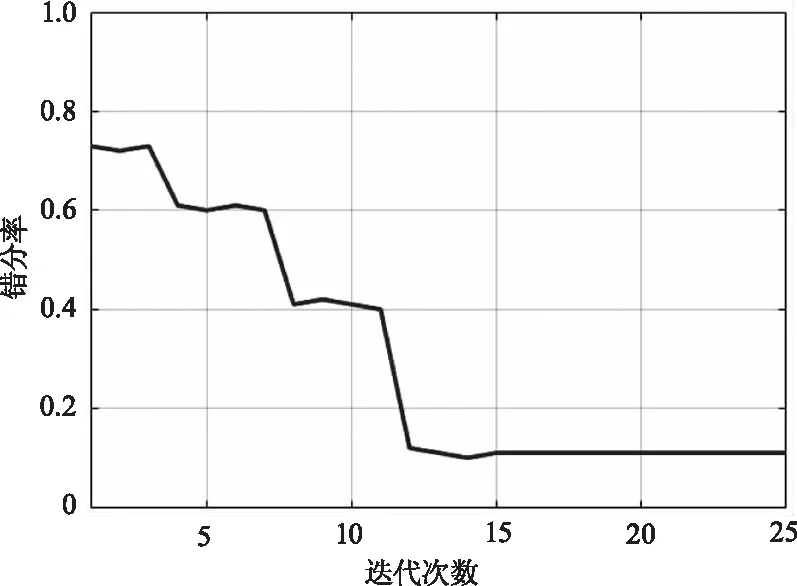
图4 GSAA-SVDD迭代过程中错分率变化曲线

图5(a)和图5(b)分别给出了利用最优SVDD分类面对两种试验场景进行FOD检测得到的结果,其中“○”代表训练样本集(杂波信号)特征,虚线“--”为训练阶段得到的最优SVDD分类面,“※”代表测试数据集中的FOD回波信号特征,“□”代表测试数据集中的杂波信号特征。需要指出的是,与文献[7]类似,试验所用毫米波雷达采用机械扫描方式,扫描过每个检测单元均会有一定驻留时间,即一个FOD会对应多次回波信号,同时为了降低漏警率,对每次回波信号均提取特征并进行判决,只要有一次回波被判为FOD,就认为该区域存在FOD,因此图5中会出现同一FOD对应多个特征标号的情况。从图5所示结果可以看出,对于两种试验场景,全部FOD回波信号特征均处于最优分类面以外,全部杂波信号特征均处于最优分类面以内,即所提方法在两种试验场景情况下能够消除虚警,实现对FOD的准确检测。

为了进一步验证所提算法的FOD检测鲁棒性,采取将高尔夫球和砖块随机放置在雷达探测范围内(半径70 m,前向±60°),利用雷达采集记录数据并利用所提方法进行FOD检测,重复进行300次试验(高尔夫球100次,砖块100次,高尔夫球和砖块一起100次)并对结果进行统计的方式开展验证。同时为了对比,分别采用传统CM-CFAR方法,文献[7]所提CM-CFAR-SVDD和文献[8]所提PSO-SVDD方法在相同条件下开展试验,以评估不同方法的优劣。表1给出了四种方法在三种不同场景下的检测概率pf和虚警概率pf,可以看出CM-CFAR-SVDD的检测概率在三种场景下相对于CM-CFAR方法分别提升14 %,13 %和14 %,但是由于两种方法都采用了CM-CFAR进行杂波抑制,所以其虚警概率略优于CM-CFAR方法,差距在2 %以内；而PSO-SVDD方法通过PSO算法对SVDD优化,提升了SVDD的检测性能,因此其检测概率优于CM-CFAR-SVDD方法,三种场景下分别提升2 %,4 %和4 %,但是由于PSO-SVDD方法采用的是CA-CFAR进行杂波抑制,所以其虚警率受制于CA-CFAR的性能,略低于CM-CFAR-SVDD方法,差距在2 %以内；本文方法利用双谱特征提取+SVDD的模式分类方法代替传统CFAR方法进行杂波抑制,因此虚警概率是四种方法中最低的,三种场景下相对于虚警率最低的CM-CFAR-SVDD方法分别低约3 %,3 %和4 %,同时GSAA优化后的SVDD分类器也可以获得最优的检测性能,三种场景下相对于检测概率最高的PSO-SVDD方法提升超过3 %。

图5 所提方法FOD检测结果

5 结 论

复杂杂波背景下实现静止小目标检测是毫米波FOD检测雷达面临的关键问题,传统基于CFAR的检测方法普遍存在虚警率高,检测性能较差的问题。本文借鉴模式识别中异常数据检测的思路提出一种基于双谱特征提取和SVDD一类分类器的FOD检测方法,通过双谱分析提升FOD和杂波信号的可分性,然后通过双谱熵和二阶统计量特征提取实现降维,最后通过SVDD一类分类器完成FOD检测,针对SVDD核参数和惩罚因子设置问题,利用GSAA算法进行优化,提升检测性能。基于实际机场跑道数据的试验结果表明,所提方法相对于对比方法在三种试验场景下均能获得最优的检测概率和最低的虚警概率,检测概率和虚警概率的提升均超过3 %,具有较强的应用前景。