片上温漂补偿的压阻式压力芯片的设计与制造
2022-07-09李舜华聂泳忠李腾跃吴桂珊杨文奇
李舜华聂泳忠李腾跃吴桂珊杨文奇
(西人马联合测控(泉州)科技有限公司,福建 泉州 362011)
微机电系统(Micro Electro Mechanical System,MEMS)硅压阻式压力传感器具有灵敏度高、动态响应快、测量精度高、稳定性好、工作温度范围宽、易于小型化与微型化和便于批量生产等优点[1-2]。 其原理主要是基于硅的压阻效应,受到压力后其电阻率发生改变[3]。 但压阻效应受温度影响很大,在不同的工作温度下传感器的灵敏度不同,即会导致热灵敏度温漂(以变化百分比作为单位时,等同于“热满量程温漂”),严重影响传感器的标定与使用,如果不加以补偿,温度较高时传感器的灵敏度会变得比较低。
目前常用的实现低温漂的方法主要有硬件补偿和软件补偿。 业界往往采用外部电阻网络进行硬件补偿,其原理是利用电阻元件的串并联以及阻值随温度变化的特性进行温补[4],如厚膜电阻补偿技术[5]。 软件补偿是将调理芯片与压力传感器结合起来,利用软件算法对传感器的温漂进行修正[6]。但是这些补偿方法使用的调理电路不能在高温下正常工作,电路元器件往往限制了压力传感器的应用温度。 基于上述问题,一些研究者也在思考如何在芯片上进行温漂补偿,但是大部分的研究都是关于注入浓度的优化[7],这种方法局限性较大。 本研究通过在压力芯片上集成多晶硅NTC 热敏电阻,实现了压力传感器的灵敏度补偿。
1 原理分析
当材料受到应力作用产生应变时,其机械性质与电学性质会发生改变,其电阻的变化程度(用应变灵敏系数G表示)的表达式如式(1)所示[8]:
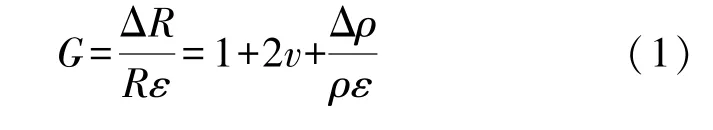
式中:为应变,R为电阻值,ΔR为电阻变化量,v为材料的泊松比,ρ为材料电阻率,Δρ为材料电阻率变化量。 应变灵敏系数G的值主要受到两部分影响,一是几何尺寸上变化,二是电阻率ρ的变化。 前者是金属应变计的主要原理,金属材料的G值只有大约2~5;而压阻效应导致的电阻率ρ的变化非常显著,因此G值也很高,P 型掺杂的单晶硅可以达到约200[8]。
掺杂半导体的应变灵敏系数G主要来源是半导体材料受到应力作用产生压阻效应,电阻率ρ发生变化,其阻值的变化量可以近似用式(2)表示[8]:
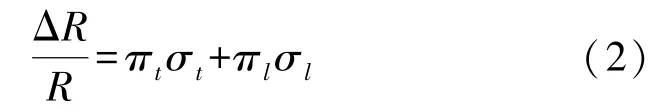
式中:π 为压阻系数,σ为应力,而下标t代表transverse(横向),即应力方向与电流方向垂直,下标l代表longitude(纵向),即应力方向与电流方向平行,其值可以由式(3)得到[9]:
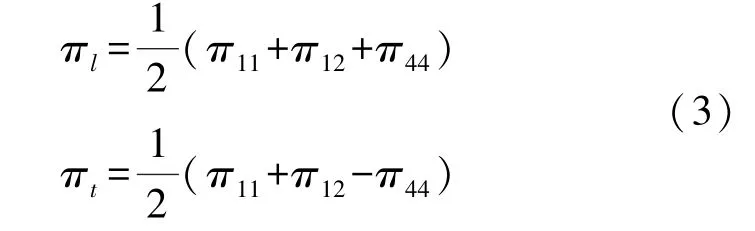
式中:π11、π12、π44为正交晶系中的压阻系数张量,当P 型掺杂单晶硅的掺杂浓度小于1×1018cm-3时,在其(100)晶面上,沿<110>晶向的纵向压阻系数πl约 为72 × 10-11/Pa,横 向 压 阻 系 数πt约 为-65×10-11/Pa[10],压阻系数越大,芯片的灵敏度越高,并且纵向压阻系数与横向压阻系数为一正一负,绝对值相近,易于构成惠斯通电桥电路,因此通常选择在单晶硅的(100)晶面上通过掺杂制备压敏电阻,并将其对准<110>晶向。
压阻系数π直接关系到芯片的灵敏度,压阻效应的原理是载流子迁移率μ的改变,对于非极性晶体来说,载流子迁移率μ的表达式如式(4)所示[11]:

式中:μI是电离杂质的散射引起的迁移率,μDP是形变势散射迁移率。
当晶格热振动的纵向声学波在晶体中传播时,发生局部形变,使导带底或价带顶发生移动,使不同地点上导带底的电子或价带顶的空穴产生能量差,称之为形变势。 当晶体膨胀时,点阵距离增加,原子之间的力常数减小,原子的均方位移增大,格波振幅增加,形变势增加,对载流子的散射作用增强,其迁移率μDP下降,因而电阻率增加[11]。 温度同样会作用于迁移率μ,但会同时作用于μI和μDP,其与温度T和杂质浓度Nd存在式(5)所示的关系[12]:

可见温度对迁移率的影响作用大于压阻效应引起的迁移率影响,换句话说,电阻温度系数TCR 与压阻温度系数并不存在直接的对应关系。 为了方便描述,在此引入一个压阻因子PF(Piezoresistance Factor),以此系数表征综合了压阻系数、电阻本身阻值等因素后的温度效应,其定义为[9]:
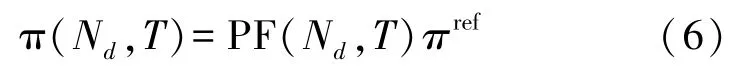
即压阻系数π 是一个与杂质掺杂浓度Nd和温度T有关的函数,πref是轻掺杂硅(1×1016cm-3)在300 K时的压阻系数。 PF 的表达式可以用Richter 模型来拟合[13]:
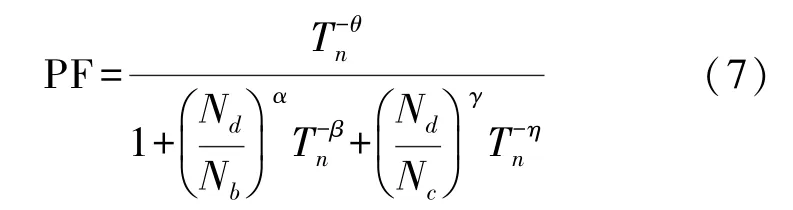
式中:Tn为实际温度T与参考温度Tref之比,由于πref的参考温度是300K,因此Tref也为300K;其余系数采 用Richter 模 型[9]的 参 数:θ=0.95,Nd=4.9×1019cm-3,Nc=2.6E20 cm-3,α=0.39,β=1.35,γ=0.94,η=4.55。
藉此可以作出不同的杂质浓度下,压阻因子PF随温度的变化曲线如图1 所示,压阻温度系数(Temperature Coefficient of Piezoresistance Factor,TCPF)为该曲线的斜率。 由图1 可知,压阻因子总是随着温度的升高而减小,杂质掺杂浓度Nd越高,TCPF 的值越小,均一性越高,即PF 的线性度越好。压阻式压力芯片的TCPF 总是小于0,导致灵敏度随着温度的升高而下降,所以当芯片工作在恒压源供电模式下时,在惠斯通电桥电路外串接一个起分压作用的补偿电阻,补偿电阻的TCR 与电桥等效电阻的TCR 不同时,温度的变化会引起其分压关系的改变。 假设电桥等效电阻值为R,桥臂电阻TCR 为α1,补偿阻值为RS,补偿电阻的TCR 为α2,当温度变化ΔT时,分压公式如式(8)所示:
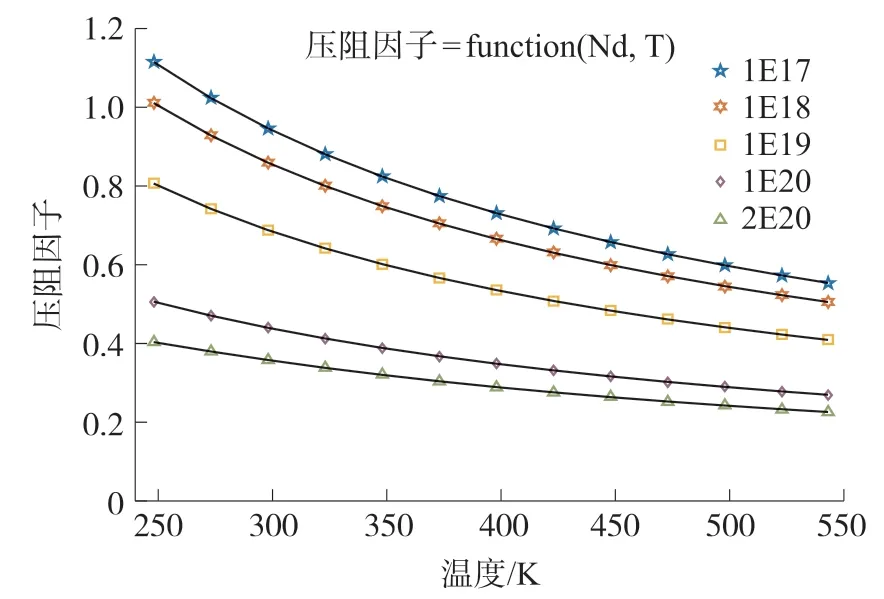
图1 不同掺杂浓度下的压阻因子PF 与温度T(K)的关系
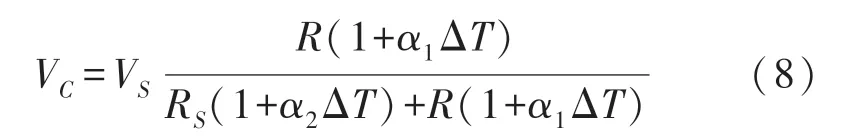
式中:VC为惠斯通电桥的端电压,VS为供电电压,α1为电桥等效电阻的TCR,由于惠斯通电桥电路的特点,α1与其桥臂单晶硅压敏电阻的温度系数相同,α2为补偿电阻的TCR,ΔT为某一温度与参考温度(300 K)之差。 在某个压力下,压敏电阻在芯片上的受力情况完全对称,阻值变化量都是ΔR,如图2 所示。
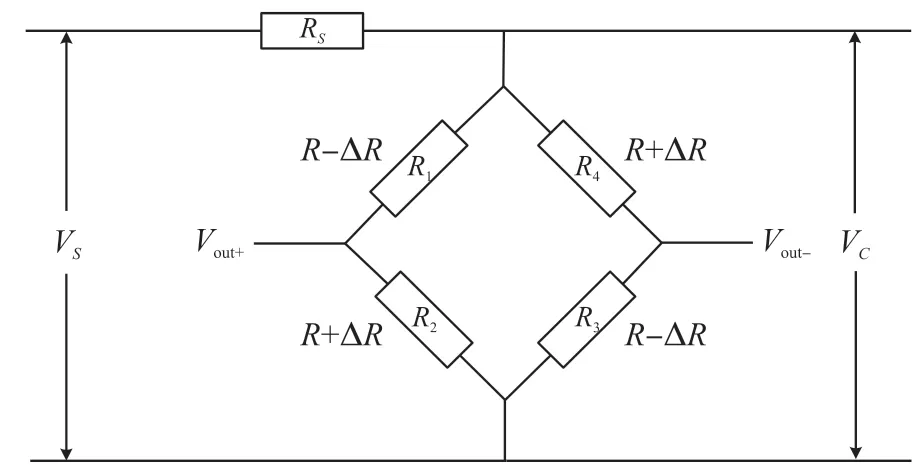
图2 等效电路示意图
因此可以得到:
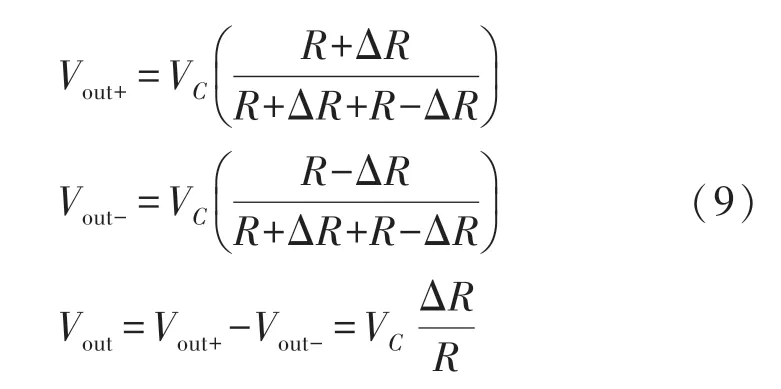
因此通过计算,选用电阻值与TCR 合适的补偿电阻,可以减小或消除TCPF 的影响。 若芯片工作在恒流源供电模式下,则可以在惠斯通电桥电路外并接补偿电阻起到分流的作用,然而需要特别指出的是,恒流源供电的惠斯通电桥电路的电压输出值,会由于其电阻的TCR 而起到自补偿的作用,因此补偿电阻的计算与恒压源供电模式时不同,在本文中着重讲述恒压源供电模式时的补偿方法。
联立式(2)、式(6)、式(7),取πl=πt,可以得到压敏电阻的灵敏度随温度的变化公式,式中的Nd取某一个定值:
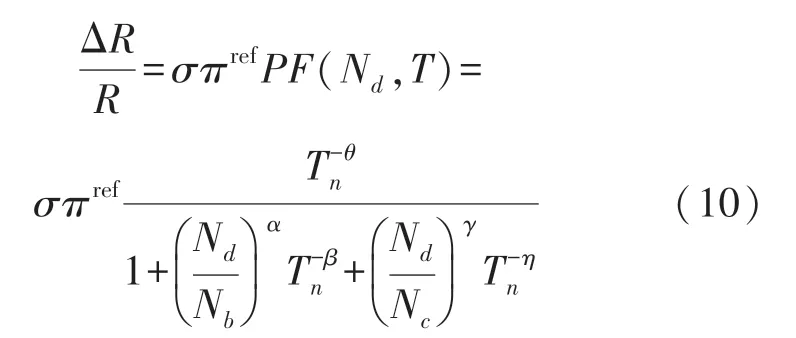
联立式(8)、式(9)、式(10),可以得到芯片的输出变化公式:
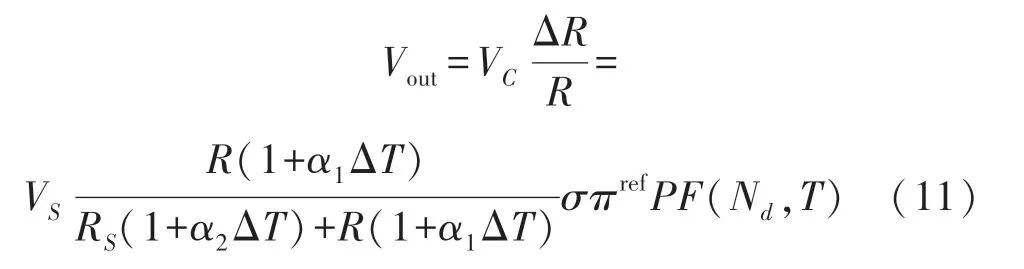
显然,补偿的目标是令其在任何温度下都趋近或保持为同一个定值,即:
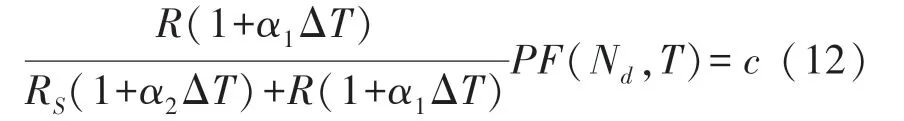
式中:温度T的相关项之积为一个任意实数c。
式(12)的第一项可以写作:
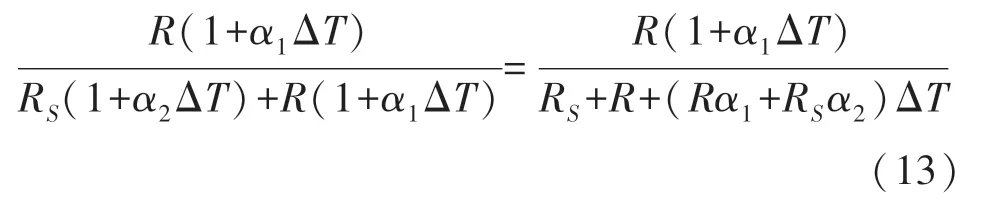
当式(13)的等号右边的分母项中的Rα1+RSα2=0 时,式(13)的第一项可以转化成一次函数的形式。可以通过改变式(13)等号右边的分子项Rα1来调节该一次函数,获得不同的补偿效果。 若不希望Rα1的值发生改变(即不改变已有结构和掺杂条件),考虑更加特殊的Rα1+RSα2≠0 的情况,该项为一个带负次项的非线性多项式,展开式(12)并移向得到补偿方程的完全表达式(14):
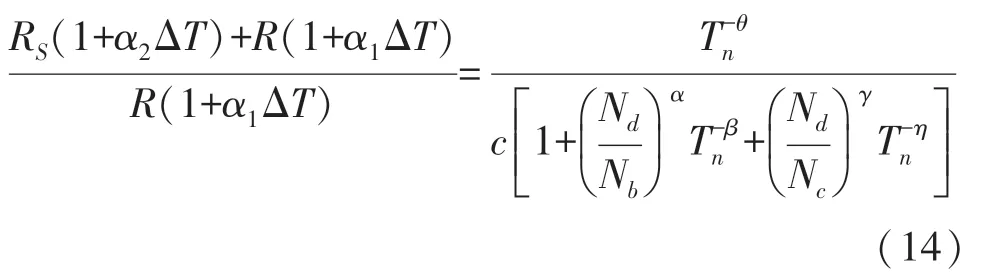
为了方便描述,还是将式(14)等号右边的项用PF 函数代表,如式(15):

如图1 所示,在高掺杂浓度的条件下,TCPF 近似为一个定值,即PF 函数可以转化成近似一次函数的形式,并且总能找到一个常数c0,使得c0PF=1,因此有:
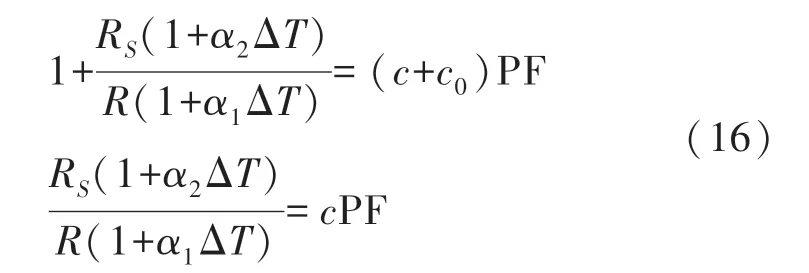
式(16)显示,补偿电阻的设计实际上是解补偿方程问题,通过调节RS和α2,使得两个曲线最接近;而RS和R既与光刻图案有关,也受杂质掺杂浓度影响,因此其值在一定程度上可以通过光刻图案控制。该方程的实际参数见下文结合具体情况分析。
2 补偿方案与数值设计
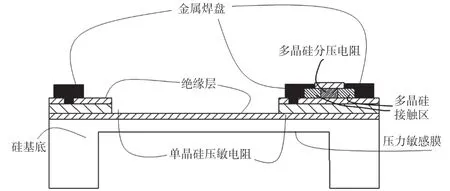
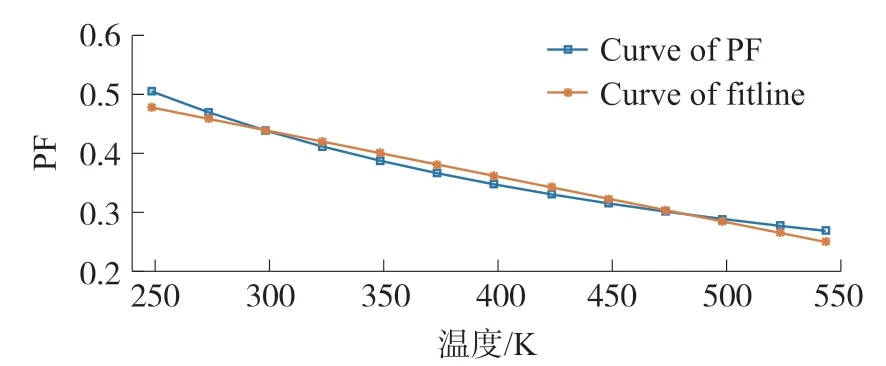
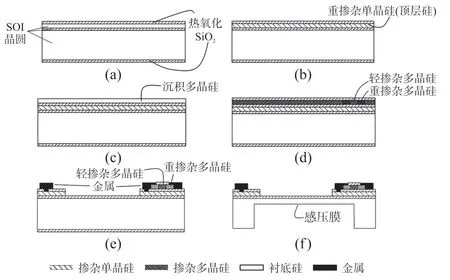
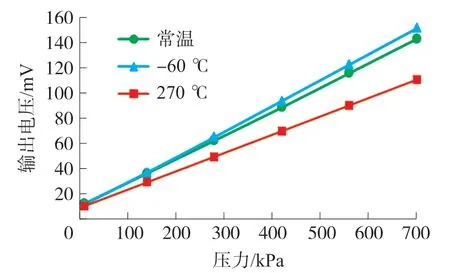
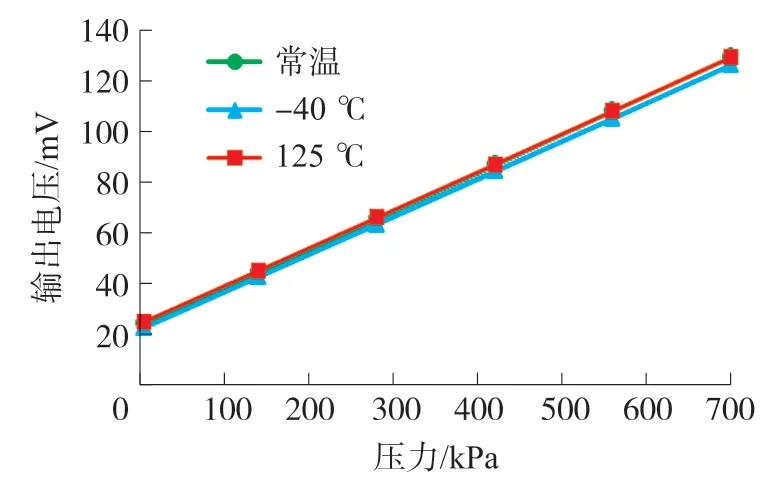
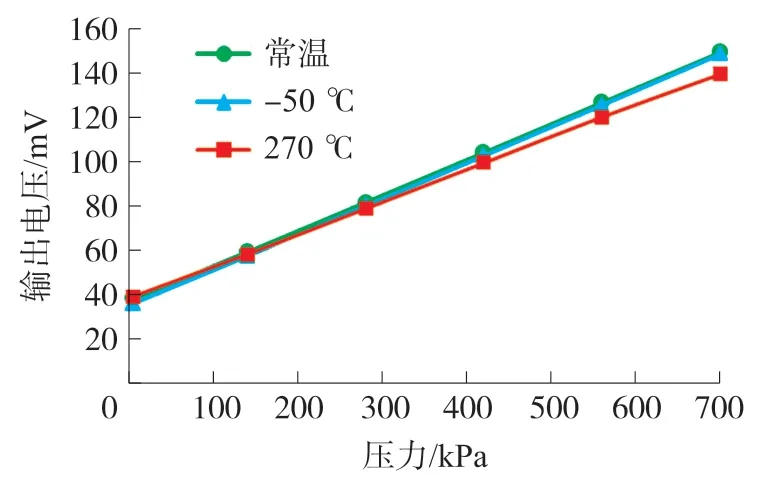
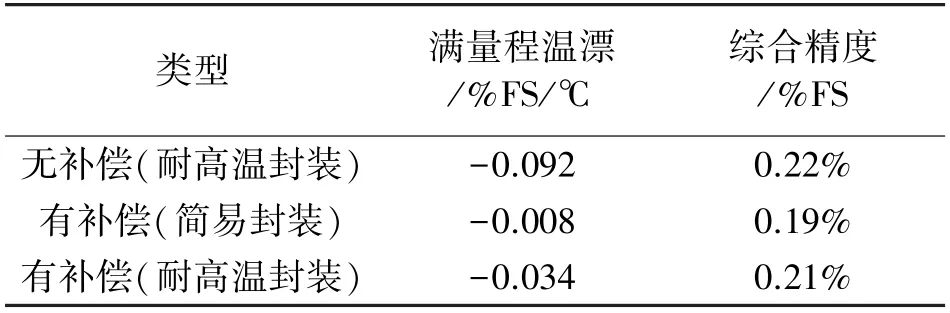
补偿电阻除了起到补偿其温度特性的作用外,还会降低其灵敏度(VC 为了在片上实现压力传感器温漂补偿,需要在芯片上制备阻值可控的NTC 电阻,所以本文采用兼容MEMS 工艺的多晶硅材料制备NTC 电阻。 多晶硅的温度系数会随着其杂质掺杂浓度的不同而改变,如图3 所示。 图3 多晶硅的电阻率和温度系数与掺杂浓度的关系[14] 通常来说,多晶硅可以用作为压敏电阻的材料,通过合理的选择杂质掺杂条件,获得更低的温度敏感特性,这是另一种低温漂压力芯片的设计思路。而采用单晶硅虽然温度敏感特性更大,但是其灵敏度也更高,通过多晶硅NTC 电阻补偿后,可以获得高灵敏度低温漂的压力芯片,本例中的结构示意图如图4 所示。 图4 芯片截面示意图 在本文中,不过多赘述芯片的结构及尺寸参数的设计原理,在此仅做一些简单的、不涉及加工误差的描述,以提出一个具体的实例便于讨论。 芯片的尺寸设计为1 mm×1 mm×0.35 mm;感压膜区域为芯片正中央的方形区域,尺寸为0.7 mm×0.7 mm 的方形并且将四个角设计为一定尺寸的圆角,以减少边角的应力集中导致感压膜破裂的可能性,厚度为26 μm;感压电路的桥臂电阻800 Ω(表面浓度约2×1020cm-3,方阻值约8 Ω/Sq),温度系数α1为1.65×10-3,当表面浓度为2×1020cm-3时,TCPF 的曲线和拟合直线图5 所示,该拟合直线的表达式如式(17)所示: 图5 2E20 cm-3浓度时TCPF 曲线及拟合直线 在无补偿时,其满量程输出为140 mV,为了不使其满量程输出过低(降低到90 mV 以下),补偿电阻阻值RS要限制在470 Ω 以下。 在本例中以1×1014cm-3注入剂量的硼离子掺杂,得到的多晶硅材料的温度系数α2约-2.75×10-3,将相关系数代入补偿方程式(15),解得RS≈300 Ω,此时满量程输出为101.8 mV,在这个条件下,可以使得压力芯片灵敏度对温度的敏感程度降到最低。 本文选用SOI 作为压力芯片的基底材料,使得芯片可以在125 ℃以上的环境下工作[15-17],压力芯片的制备步骤如图6 所示,包括如下步骤: ①SOI 晶圆(P 型顶层硅厚度1 μm,中间层氧化硅厚度1 μm,基底硅,共三层),经RCA 清洗后,进行高温炉管氧化,形成230 nm(±20 nm)的SiO2绝缘层,如图6(a)所示; 图6 芯片关键工艺流程图 ②以热氧产生的SiO2层作为掩蔽层,对正面(顶层硅面)进行P 型离子注入(硼注入),注入剂量2×1016cm-3,加高温退火使得顶层硅被完全掺杂,使得顶层硅内的杂质浓度约为2×1020cm-3,如图6(b)所示; ③利用低压化学气相沉积(LPCVD)工艺在正面氧化层上沉积800nm(±50nm)的多晶硅,如图6(c)所示; ④对正面行P 型离子注入,注入剂量1×1014cm-3(与电极接触的区域额外注入4×1015cm-3,减少接触电阻),并高温退火,如图6 所示; ⑤依次对多晶硅-氧化硅-单晶硅进行图形化刻蚀,只留下设计好的惠斯通电桥图形,而后利用物理气相沉积(PVD)工艺 在电路的各个电极处沉积Ti/Pt/Au 金属层,如图6(e)所示; ⑥硅片背部进行减薄至晶圆厚度为350 μm后,采用深反应离子刻蚀(DRIE)工艺刻蚀腔体,深度为324 μm(留下26 μm 厚的感压膜),如图6(f)所示; ⑦最终的成品,可以选择在底部键合硼硅玻璃(BF33),以改善芯片的精度性能。 最终制备的压力芯片实物图如图7(a)所示(芯片底部键合700 mm 厚度的无通孔BF33 玻璃,测量的压力类型为绝对压力),本文着重探究芯片的性能,因此选用尽可能简单的封装方式,以压力传感器性能表征最原始的压力芯片性能,简易封装后的压力传感器实物图如图7(b)所示,但为了测量更高温度下的性能,需要采用耐高温的封装,如图7(c)所示。 图7 压力芯片及压力传感器示意图 如图8 所示,测试环境主要由压力控制器(误差±0.01%),高精度稳压电源(±0.01 V)和数字万用表组成。 供电电压为10 V。 在0~700 kPa(绝对压力)范围内选取6个测试点(包括零点),测试方法按JJG 860-2015«压力传感器(静态)检定规程»测试。 无补偿的芯片的输出曲线如图9 所示,补偿后的不同封装方式的芯片输出曲线如图10 和图11 所示。 图8 测试环境示意图 图9 无补偿芯片(耐高温封装)输出特性曲线 图10 有补偿芯片(简易封装)输出特性曲线 图11 有补偿芯片(耐高温封装)输出特性曲线 3 种传感器的性能如表1 所示,其中耐高温封装的温度测试范围为-50 ℃~270 ℃,简易封装的采用的基板是FR4 材料,故其测试温度范围为-40 ℃~125 ℃。 传感器的综合精度的计算方法为非线性、迟滞和重复性三者的算术平方根,表中的“综合精度”是分别在低温、常温和高温时测量得到的综合精度的平均值,由于掺杂多晶硅材料TCR 的非线性,随着温度升高,温度变化引起的补偿电阻阻值的变化量不足以补偿压力芯片输出的下降,导致高温下补偿效果变差,故简易封装下单位温度的满量程温漂测试结果会优于耐高温封装。 表1 性能指标对比 测试结果表明,本文的方法所设计并制造的压力传感器,在几乎不影响精度性能的同时具有较低的输出温度系数,实现了低温漂压力芯片的设计与制作,解决了不同温度下压力传感器的输出差异大,影响标定的应用难题。 本文通过理论计算和实际测试验证,分析了硅压阻式压力芯片的灵敏度对温度敏感的原因及其底层规律,并采用芯片上集成NTC 分压电阻的方式进行补偿,根据一个具体的实例完成了一系列数值的计算,确定最优补偿值。 本文还设计了相应的芯片流片工艺,将所设计的芯片实际加工完成,并将其封装成传感器进行性能测试。 性能测试结果显示P型掺杂的多晶硅补偿电阻显著地降低了芯片的灵敏度温漂,在-50 ℃~270 ℃温度区间内温漂降低至-0.034% FS/℃,约为无补偿传感器的1/3。 此外在实验过程中发现,掺杂多晶硅的温度系数线性度较差,温度越高时其温度系数的变化量绝对值越小,会导致补偿效果下降,因而在-40 ℃~125 ℃温度区间内整体的温漂补偿效果会更好,为-0.008% FS/℃,为无补偿传感器的1/10。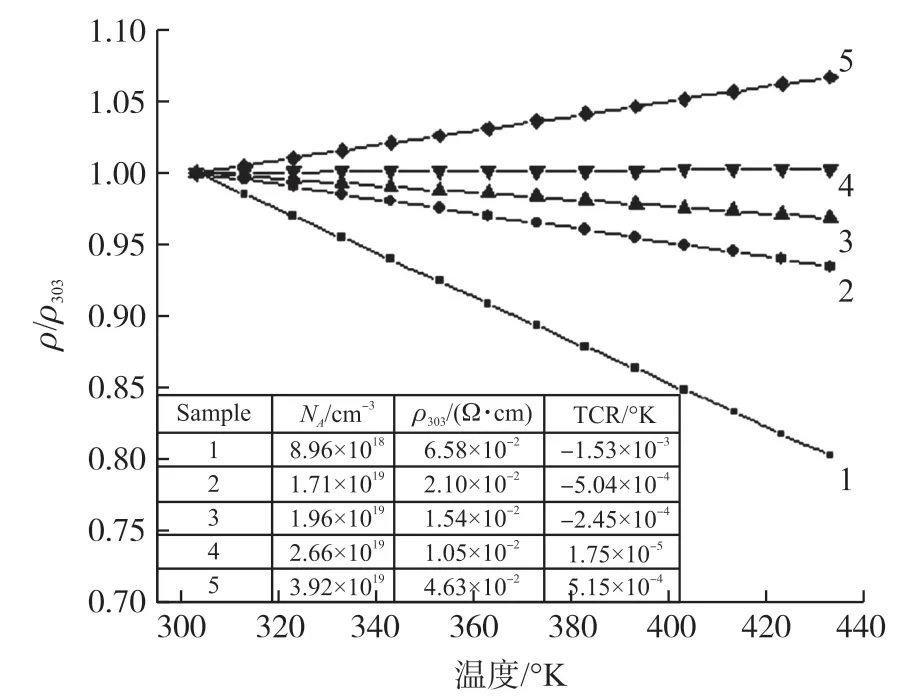
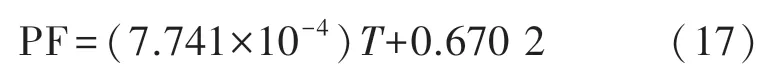
3 芯片流片工艺
4 封装与测试


5 结论
