基于蝶翼式MEMS 振动传感器的轴承故障信号检测方法

2022-07-09蒲金飞侯占强吴学忠肖定邦曾承志陈伟琪李修文

传感技术学报 2022年4期

蒲金飞侯占强吴学忠*肖定邦曾承志陈伟琪李修文

(1.国防科技大学智能科学学院，湖南长沙 410073；2. 唐智科技湖南发展有限公司，湖南长沙 410007)

轴承被广泛应用于航空航天、轨道交通、冶金、电力、矿山、机械、石油、煤炭、造纸等行业。然而，轴承故障是旋转机械最易发生故障的零件，轴承一旦出现故障，将影响整个机械的正常运行，因此，对轴承进行有效的状态监测具有重要意义。

轴承在运转过程中，其振动信号、声发射信号、温度信号中隐含了大量的状态信息，其中振动信号应用最为广泛[1]。振动传感器一般采用压电式振动传感方式或MEMS 振动传感方式[2－3]，当前对基于振动信号的轴承故障诊断研究主要分二个方面，一是对振动信号处理技术的研究[4－5]，二是对振动传感器的设计优化。对于振动信号的处理主要包括对振动信号的时域分析、频域分析、时频分析等[6]。在时域内对振动信号进行滤波、放大、统计特征计算、相关性分析等处理，统称为振动信号的时域分析，其中最大值、最小值、均值、标准差、有效值、方差等时域特征参数主要适用于稳态振动的情况[7]，而峭度指标等时域特征参数则主要适用于判断冲击类故障特征[8]。振动频域分析泛指通过振动传感器获取轴承的振动信号，经傅里叶变换处理后求出振动信号的幅值谱、功率谱、相位谱和倒谱等，然后与轴承的故障频谱图进行对比分析，从而判断轴承是否存在故障以及故障的严重程度。振动频域分析需要根据频谱幅值的大小来判断故障的严重程度，受噪声和背景干扰影响较大，对早期故障的诊断存在一定的局限性。由于单一的时域分析和频域分析均不能全面地表征故障信息，因此研究人员对振动信号的时频分析方法进行了研究。例如，Huang[9]将同步压缩变换扩展到S 变换的时频表示上，获得了较好的时频聚集性；由于同步压缩变换及其扩展方法适用于由弱频率调制模式组成的信号，为了分析强调频模式的多分量信号，Oberlin[10]提出了一种基于相位近似的二阶同步压缩变换；Hu[11]提出的基于小波的高阶同步压缩变换和Pham[12]提出的基于短时傅里叶变换的高阶同步压缩变换，对低频分量和高频分量都能提供良好的时频分辨率；Yu[13]将迭代重分配算子引入到同步压缩变换中，提出了多同步压缩变换，多次迭代重分配能量系数，让信号的时频表示更加聚集，获得更加清晰的时频表示；Yu和林凯[14－15]分别提出了基于短时傅里叶变换的二阶多同步压缩变换和基于S 的多同步压缩变换。传统的时频分析方法虽能比较全面地从振动信号中挖掘特征，但也受海森堡测不准原理及交叉项的影响。

本文提出了一种基于蝶翼式MEMS 振动传感器的轴承故障信号检测方法，在振动信号检测环节实现对轴承故障信号的有效敏感，更加有利于后续数据信号处理，提高轴承故障检测的有效性。

1 蝶翼式MEMS 振动传感器与电子谐振器级联的轴承故障信号检测方法

基于蝶翼式MEMS 振动传感器本身优异的机械谐振特性，在其后级联一个电子谐振器形成两级谐振系统，用于对轴承故障信号进行检测，其原理框图如图1 所示。

图1 轴承故障信号检测方法原理框图

轴承故障信号一般表现为幅值小、持续时间短、频带宽的振动信号，其时域表达式可表示为:

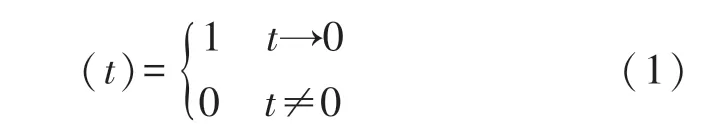
由于故障信号中含有丰富的频率成分，一般都能激发传感器自身的振动响应，其响应频率总是等于传感器自身的谐振频率，并将故障信号幅度放大，此过程为第一级谐振过程。

受制造工艺的影响，传感器的谐振频率、品质因数等参数会存在一定程度的离散性，给故障信号的分析和精确诊断带来影响。考虑到电子谐振器与机械谐振系统具有等效性，且比机械谐振具有更好的可控性和可实现性，因此在传感器机械谐振之后增加一个电子谐振器，用于对传感器机械谐振的输出信号进行归一化、放大、降频和滤波处理，把更高频的机械谐振信号转换为稍低频的电子谐振信号，更加精确地控制谐振频率、品质因数、带宽并抑制低频振动信号，此过程为第二级谐振过程。

对电子谐振器的输出信号进行绝对值检波和包络解调后通过AD 采集实现数字化转换，再由后级的故障诊断算法实现故障的定性和定量诊断。

为验证所提方法的有效性，利用Tina 进行仿真。仿真输入信号由100 Hz 的故障信号和频率分别为1 800 Hz、2 000 Hz 和500 Hz 的常规振动信号组成，仿真结果如图2 所示。由图2 可知:蝶翼式MEMS 振动传感器与电子谐振器级联的轴承故障信号检测方法实现了对故障信号的放大和常规振动信号的分离，对故障信号具有选择性、对应性、比例性、放大性、展宽性和低频性等特性，能够对故障信号进行有效检测。

图2 轴承故障信号检测方法仿真

该方法中，蝶翼式MEMS 振动传感器和电子谐振器的设计是关键。其中，蝶翼式MEMS 振动传感器设计的基本原则为:谐振频率要远高于被检测轴承故障信号的频率，并高于电子谐振器的中心频率，品质因数Q 应不小于10；电子谐振器设计的基本原则为:电子谐振器的中心频率要远高于被检测轴承的最高旋转频率，品质因数Q 应不小于5，通带波动应小于等于1 dB，带外衰减应大于30 dB/oct。

2 蝶翼式MEMS 振动传感器设计与加工

2.1 双扭摆全差分敏感结构

敏感结构由硅敏感结构和玻璃基板组成，硅敏感结构采用四质量块双扭摆全差分结构[16]，在玻璃基板上制作检测电极，检测电极与质量块之间形成检测电容，如图3(a)所示。锚点和扭转梁内置于质量块内，将可用面积最大限度地用来构成质量块与检测电极之间的检测电容面积，使敏感结构更加紧凑的同时有助于进一步提升敏感结构的灵敏度；应力释放结构有助于释放结构应力，从而降低结构应力对敏感结构性能的影响，进一步提升工作稳定性。

图3 敏感结构及其工作原理示意图

当外界存在加速度作用时，在惯性力的作用下，两对非平衡质量块绕扭转梁做反向扭摆运动，使检测电容极板之间的距离发生变化，进而引起检测电容发生变化，敏感结构的工作原理示意图如图3(b)所示。通过电容检测电路检测出电容量在加速度作用下的变化，并建立该电容量变化与加速度之间的关系，即可实现对加速度的检测。加速度a、非平衡质量块的扭转角度φ与检测电容变化量ΔC之间的具有如下关系:

利用COMSOL 软件对敏感结构的模态进行仿真并利用示波器对蝶翼式MEMS 振动传感器的谐振频率进行测试，仿真及测试结果如图4 所示。

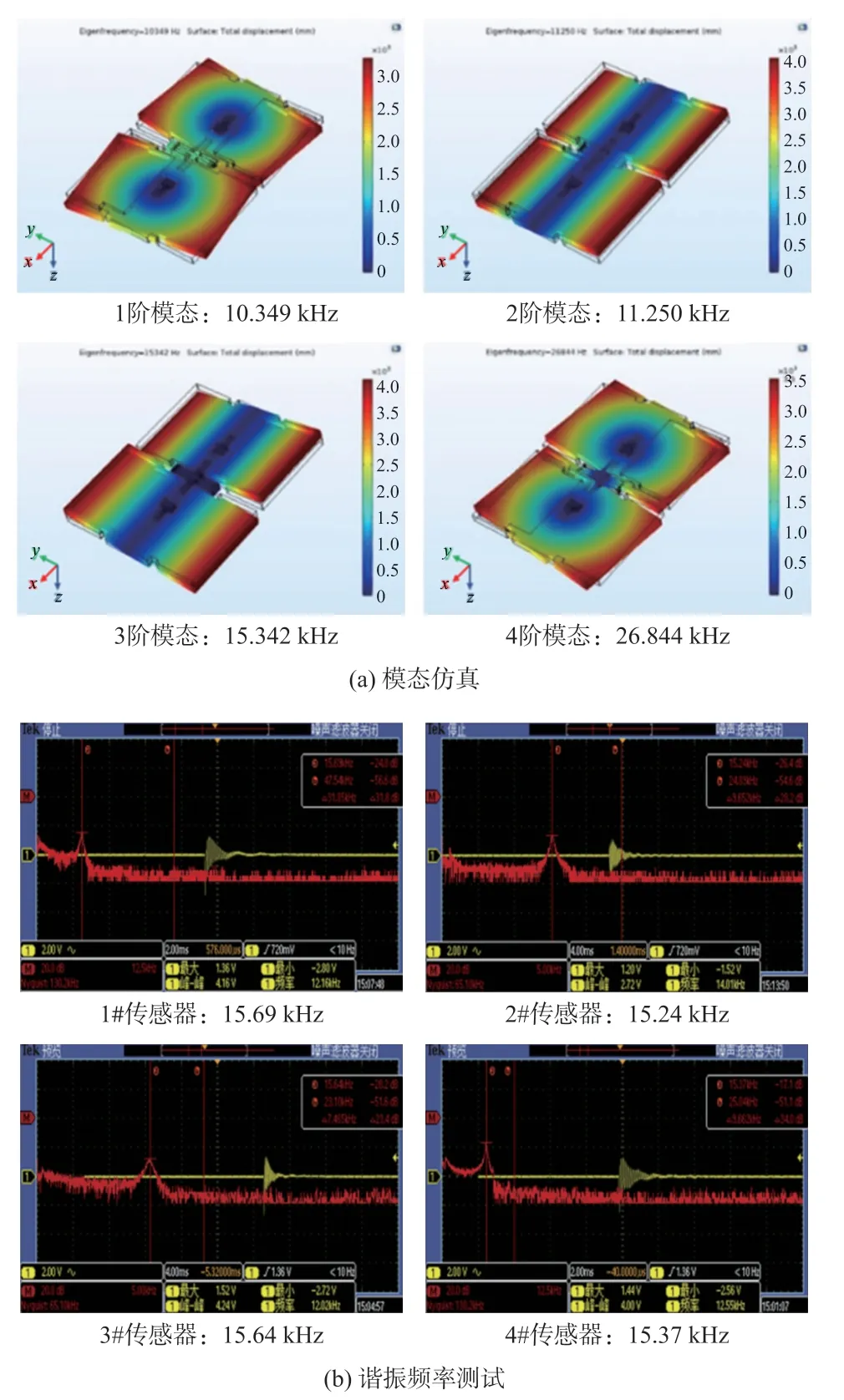
图4 模态仿真及谐振频率测试

由图4 可知:敏感结构的三阶模态为其工作模态，对应的模态频率为15.342 kHz；4 只被测传感器的谐振频率最小为15.24 kHz，最大为15. 69 kHz，实际测试结果与模态仿真结果相近。

2.2 开关电容放大检测电路

基于载波调制和开关解调原理，设计了开关电容放大检测电路，用于实现电容C到电压V的转换。开关电容放大检测电路的原理框图如图5 所示。

图5 开关电容放大检测电路原理框图

C/V 转换的输出vq(t)与检测电容变化量ΔCi(i＝1，2，3，4)的关系为:

结合蝶翼式MEMS 振动传感器的敏感结构对开关电容放大检测电路进行频率响应测试，测试结果如图6 所示。

图6 开关电容放大检测电路频率响应测试

由图6 可知:开关电容放大检测电路在0～8 kHz 范围内其输出偏差小于±2%，在0～10 kHz 范围内其输出偏差小于±4%。

2.3 加速度计加工封装

蝶翼式MEMS 振动传感器的敏感结构在结构上从下至上依次为电极基板、硅敏感结构和封装盖帽，如图7(a)所示。电极基板和硅敏感结构均采用基于SOI 硅圆片的深反应离子干法刻蚀技术加工得到，两者通过“硅－硅”低应力阳极键合技术实现固连，最后通过玻璃浆料键合技术与封装盖帽进行圆片级真空封装，其加工工艺流程如图7(b)所示，加工得到的敏感结构芯片如图7(c)所示。

图7 敏感结构结构组成、加工工艺流程及芯片实物

蝶翼式MEMS 加速度计的封装结构由陶瓷管壳、应力隔离结构、敏感结构芯片和ASIC 芯片组成，如图8(a)所示。应力隔离结构用于降低敏感结构芯片与陶瓷管壳直接接触时因热弹性系数不同引起的热应力水平。在完成ASIC 芯片和敏感结构芯片制备的基础上，本文采用DRIE 工艺实现应力隔离结构的刻蚀释放，最后实现敏感结构芯片、应力隔离结构、ASIC 芯片和陶瓷管壳的低应力互连，加速度计的封装实物如图8(b)所示。

图8 加速度计封装结构及实物

3 电子谐振器设计

电子谐振器具有带通滤波器结构，利用MAX275 连续时间有源滤波器芯片来实现，它由两组独立可级联的滤波单元组成，每组通过外部配置四个电阻实现四阶全极点带通或低通滤波器响应，中心频率范围可达到300 kHz，具有高频率精度、低噪声、外围电路简单、参数调整方便等优点。

基于上文提到的电子谐振器设计的基本原则，本文将MAX275 的两组4 阶滤波器级联组成一个8阶电子谐振器，其电路仿真模型如图9 所示。

图9 所示电路仿真模型的外围元器件参数计算公式如下:

式(4)～式(8)中，F0为中心频率，Q为品质因数，G为谐振峰值增益。

利用Tina 对图9 的电路仿真模型进行仿真并采用扫频仪对电子谐振器进行扫频测试，仿真及测试结果如图10 所示。

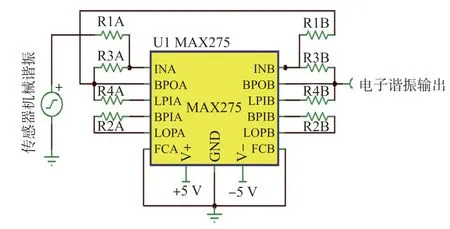
图9 电子谐振器的电路仿真模型

由图10 可知:仿真得到电子谐振器的中心频率为12.5 kHz，谐振峰值增益为11.07 dB，带内波动为0.99 dB，带外衰减为35.48 dB/oct；扫频测试得到电子谐振器的中心频率为12.1 kHz，谐振峰值增益为10.95 dB，带内波动为0. 93 dB，带外衰减为37.36 dB/oct，实际测试结果与仿真结果相近。

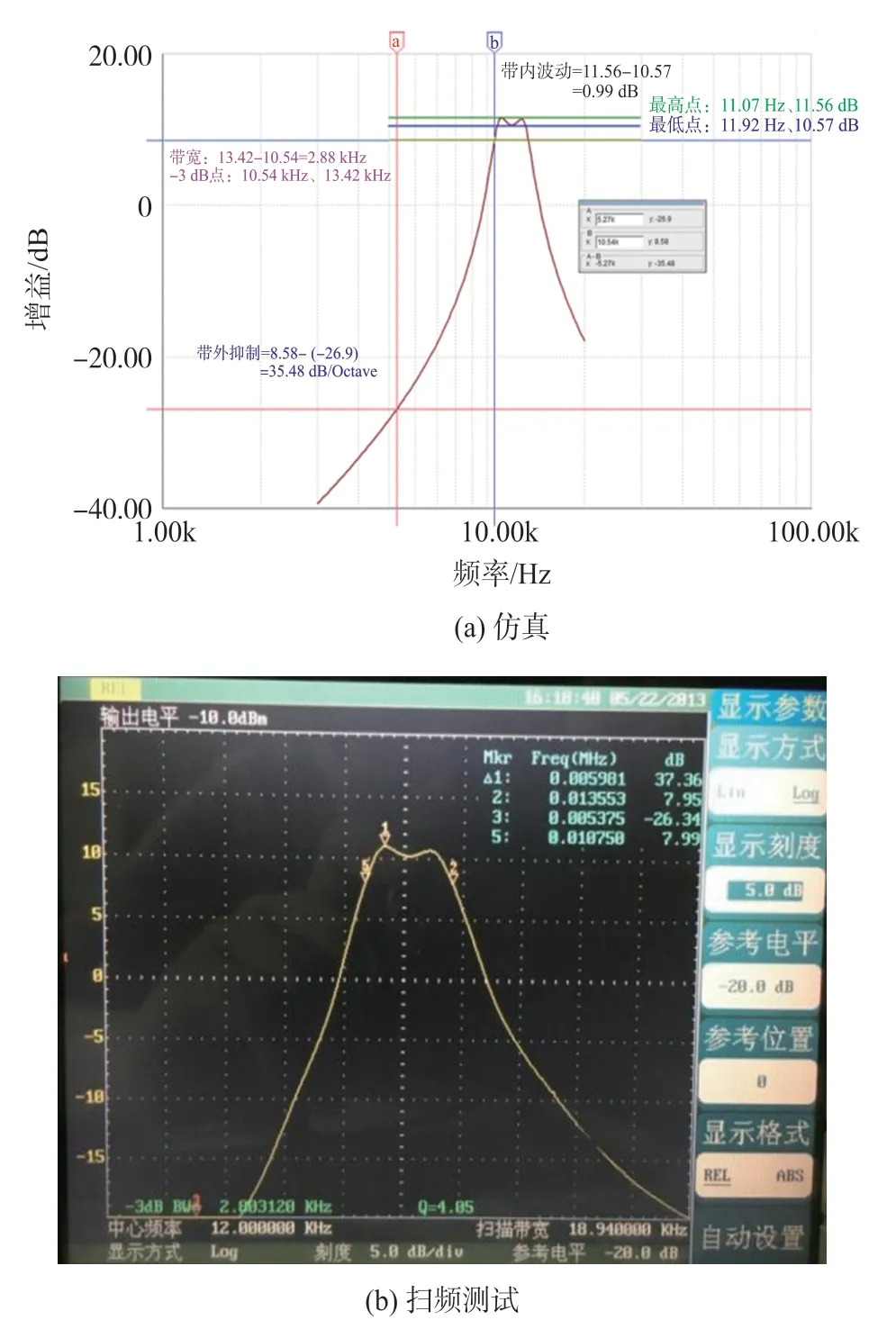
图10 电子谐振器仿真及测试

4 应用验证

利用存在外环故障的轴承，在轴承试验机上验证蝶翼式MEMS 振动传感器与电子谐振器的级联系统检测轴承故障信号的有效性，验证平台和轴承故障如图11 所示。

图11 验证平台和轴承故障

故障轴承的轴承参数如表1 所示。

表1 故障轴承参数

验证方案如下:

①由轴承试验机为故障轴承提供载荷和转速，蝶翼式MEMS 振动传感器提供一级谐振，高速采集仪中的电子谐振器提供二级谐振；

②分别在关闭和开启电子谐振器的情况下，由高速采集仪以100 k sample/s 进行数据采集，再利用MATLAB 对采集的数据进行时域和频域分析，对比一级谐振系统(仅利用蝶翼式MEMS 振动传感器的机械谐振)和蝶翼式MEMS 振动传感器与电子谐振器的级联系统对轴承故障信号的检测效果。

验证所采用的转速为439 r/min，通过计算得到外环故障理论频率为52.68 Hz。

在不开启和开启电子谐振器的情况下，轴承故障信号的时域波形和频谱图如图12 所示。

图12 时域波形和频谱图

由图12 可知:在不开启电子谐振器的情况下(仅利用蝶翼式MEMS 振动传感器的机械谐振)，从时域波形看不到明显的轴承故障信号，频谱图中在蝶翼式MEMS 振动传感器的谐振频率附近能量较突出，但外环故障的频域特征不明显；在开启电子谐振器的情况下(同时利用蝶翼式MEMS 振动传感器的机械谐振和电子谐振器的电子谐振)，从时域波形可以看到明显的轴承故障信号，频谱图中轴承外环故障的1～10 阶频谱突出，频域特征非常明显。

验证结果表明:本文提出的蝶翼式MEMS 振动传感器与电子谐振器级联的轴承故障信号检测能够有效地滤除无用的振动信号(噪声)、放大有用的故障信号，大幅提高了信噪比，可有效地提取轴承故障信号。