A Characterization of the Standard Tori in C2 as Compact Lagrangian ξ-Submanifolds∗

Xingxiao LI Ruiwei XU

1School of Mathematics and Information Sciences,Henan Normal University,Xinxiang 453007,Henan,China.E-mail: xxl@htu.edu.cn

2Corresponding author.School of Mathematics and Information Sciences,Henan Normal University,Xinxiang 453007,Henan,China.E-mail: rwxu@htu.edu.cn

Abstract In this paper,the authors give a characterization theorem for the standard tori S1(a)×S1(b),a,b>0,as the compact Lagrangian ξ-submanifolds in the two-dimensional complex Euclidean space C2,and obtain the best version of a former rigidity theorem for compact Lagrangian ξ-submanifold in C2.Furthermore,their argument in this paper also proves a new rigidity theorem which is a direct generalization of a rigidity theorem by Li and Wang for Lagrangian self-shrinkers in C2.

Keywords ξ-Submanifold,the Second fundamental form,Mean curvature vector,Standard tori

1 Introduction

Anm-dimensional submanifoldx:Mm→Rm+pin the (m+p)-dimensional Euclidean space Rm+pis called a self-shrinker (to the mean curvature flow) if its mean curvature vector fieldHsatisfies

wherex⊥is the orthogonal projection of the position vectorxto the normal spaceT⊥Mmofx.

As we know,self-shrinkers play an important role in the study of the mean curvature flow.In fact,they correspond to the self-shrinking solutions to the mean curvature flow,and describe all possible Type I singularities of the flow(see[10,12]).Up to now,various results of classification or rigidity theorems on the self-shrinkers have been obtained(see[2,14,17]).In particular,there are also interesting results about the Lagrangian self-shrinkers in the complex Euclideanmspace Cm.For example,in[1],Anciaux gives new examples of self-shrinking and self-expanding Lagrangian solutions to the mean curvature flow.In [3],the authors classify all Hamiltonian stationary Lagrangian surfaces in the complex plane C2,which are self-similar solutions of the mean curvature flow and,in [4],several rigidity results for Lagrangian mean curvature flow are obtained.In [5],Cheng-Hori-Wei obtain a complete classification for 2-dimensional complete Lagrangian self-shrinkers in Euclidean space R4with constant squared norm of the second fundamental form.In 2017,Li and Wang prove a rigidity theorem (see [13]) which gives a new characterization of the Clifford torus S1(1)×S1(1) as a Lagrangian self-shrinker,improving a previous theorem by Castro and Lerma in [4],without the additional condition that the Gauss curvatureKofM2is either non-negative or non-positive.

Theorem 1.1(see[4,13])Let x:M2→C2be a compact oriented Lagrangian self-shrinker with h its second fundamental form.If|h|2≤2,then|h|2=2and x(M2)is the Clifford torusS1(1)×S1(1),up to a holomorphic isometry onC2.

On the other hand,the first author and one of his coauthors made in 2016 a natural generalization of self-shrinkers to the concept ofξ-submanifolds(see[15]): An immersed submanifoldx:Mn→Rn+pis called aξ-submanifold if there is a parallel normal vector fieldξsuch that the mean curvature vector fieldHsatisfies (see [15])

Obviously,the affine plane R2,the standard tori S1(a)×S1(b) fora,b >0,and the circular cylinders S1(a)×R1are canonical examples of Lagrangianξ-submanifold in C2.Some other examples ofξ-submanifolds can be seen in[16].The variation characterization and the stability properties ofξ-submanifolds were also systematically studied in [16].In particular,a submanifoldx:Mm→Rm+pis aξ-submanifold if and only if its modified mean curvature is parallel when viewed as a submanifold in the Gaussian space(〈·,·〉).Extending the result of Theorem 1.1,we also proved in [15]the following rigidity theorem for Lagrangianξ-surfaces in C2.

Theorem 1.2(see[15])Let x:M2→C2be a compact oriented Lagrangian ξ-submanifold with the second fundamental form h and mean curvature vector H.Assume that

Then|h|2+|H−ξ|2≡|ξ|2+4and x(M2)=T2is a topological torus.

Furthermore,if〈H,ξ〉is constant and one of the following four conditions holds:

then,up to a holomorphic isometry onC2,x(M2)must be a standard torusS1(a)×S1(b),where a and b are positive numbers satisfying a2+b2≥2a2b2.

Then we obtain the following corollary.

Corollary 1.1(see[15])Let x:M2→C2be a compact oriented Lagrangian self-shrinker.If

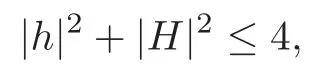
then|h|2+|H|2≡4and x(M2)=S1(1)×S1(1)up to a holomorphic isometry onC2.

This corollary gives a new rigidity theorem for self-shrinkers that is parallel to Theorem 1.1.

Clearly,ξ-submanifolds are also an extension to higher codimension of the concept ofλhypersurface which were introduced in [8]by Cheng and Wei.According to [8],a hypersurfacex:Mm→Rm+1is called aλ-hypersurface if its scalar mean curvatureHsatisfies

for some constantλ,wherenis the unit normal vector ofx.Some rigidity or classification results forλ-hypersurfaces are obtained,for example,in [6–7,11],and more recently,[9].

Note that the conditions in Theorem 1.2 seem rather tedious anyway.Thus it is interesting if one can make some simplification of the theorem.In the present paper,we are able to greatly improve Theorem 1.2 by proving the following best version of it,giving a new characterization of the standard tori as the compact Lagrangianξ-submanifolds in C2.

Theorem 1.3Let x:M2→C2be a compact oriented Lagrangian ξ-submanifold with the second fundamental form h and mean curvature vector H.If

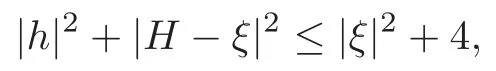
then|h|2+|H−ξ|2≡|ξ|2+4and,up to a holomorphic isometry onC2,x(M2)must be a standard torusS1(a)×S1(b)for some positive numbers a and b.

Furthermore,by a careful check of our argument in the proof of Theorem 1.3,one easily sees that the following interesting theorem also holds,which is apparently a direct generalization of the rigidity theorem by Li and Wang mentioned above (Theorem 1.1).

Theorem 1.4Let x:M2→C2be a compact oriented Lagrangian ξ-submanifold with the second fundamental form h and mean curvature vector H.If

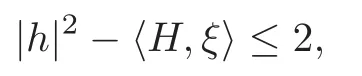
then|h|2−〈H,ξ〉≡2and,up to a holomorphic isometry onC2,x(M2)must be a standard torusS1(a)×S1(b)for some positive numbers a and b with

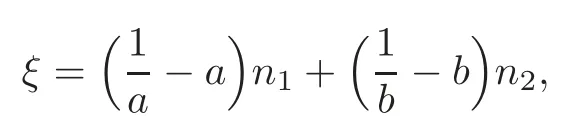
where n1,n2are the inwards unit normals ofS1(a)⊂C1andS1(b)⊂C1,respectively.

2 Lagrangian Submanifolds in Cm

Let Cmbe the complex Euclideanm-space with the canonical complex structureJ.Through out this paper,x:Mm→Cmalways denotes anm-dimensional Lagrangian submanifold,and∇,D,∇⊥denote,respectively,the Levi-Civita connections onMm,Cm,and the normal connection on the normal bundleT⊥Mm.Then the formulas of Gauss and Weingarten are respectively given by

whereX,Yare tangent vector fields onMmandηis a normal vector field ofx.The Lagrangian condition implies that

wherehandAare the second fundamental form and the shape operator ofx,respectively.In particular,〈h(X,Y),JZ〉 is totally symmetric as a 3-form,namely,

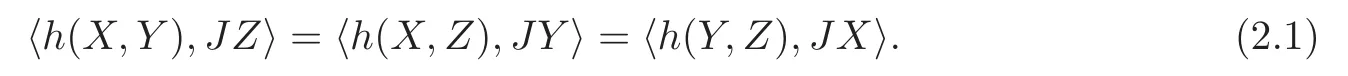
From now on,we agree with the following convention on the ranges of indices:

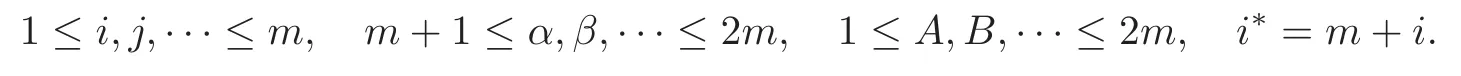
For a Lagrangian submanifoldx:Mm→Cm,there are orthonormal frame fields of the form{ei,ei∗} for Cmalongx,whereei∈T Mmandei∗=Jei.Such a frame is called an adapted Lagrangian frame field in the literature.The dual frame field is always denoted by {θi,θi∗},whereθi∗=−Jθi.Write

or equivalently,

Then (2.1) is equivalent to

Ifanddenote the connection forms of ∇and ∇⊥,respectively,then the componentsof the covariant derivatives ofhare given respectively by

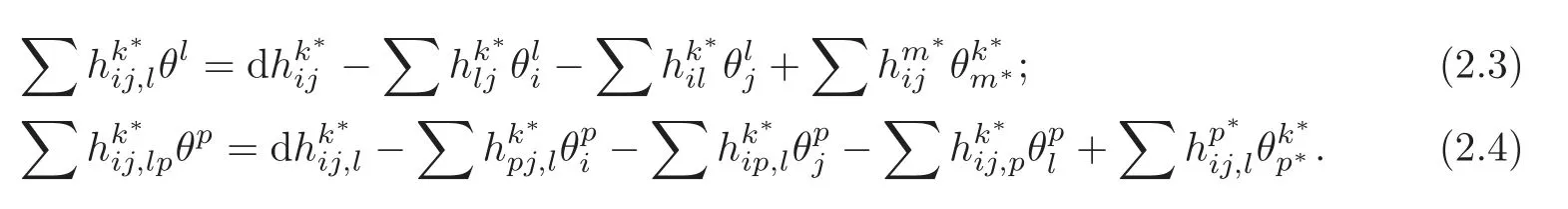
Moreover,the equations of motion are as follows:

LetRijklandRi∗j∗kldenote the components of curvature operators of ∇and ∇⊥,respectively.Then the equations of Gauss,Codazzi and Ricci are as follows:

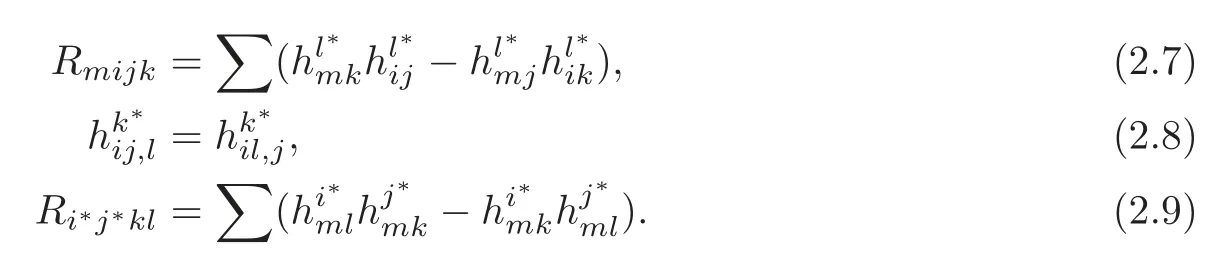
The scalar curvature of ∇is

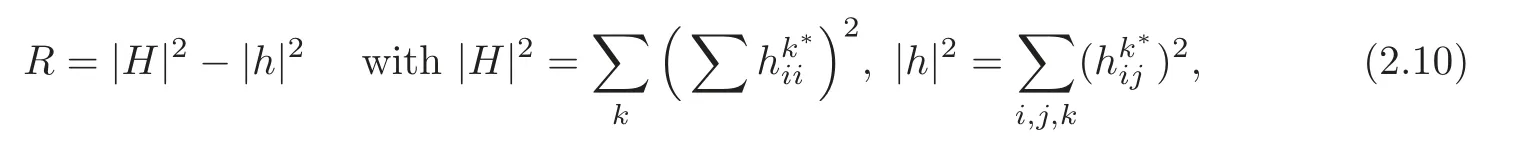
where the mean curvature vector fieldHis defined by

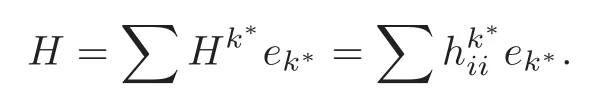
Combining (2.2) and (2.8),we know thatis totally symmetric,namely,

and the Ricci identities are as follows:

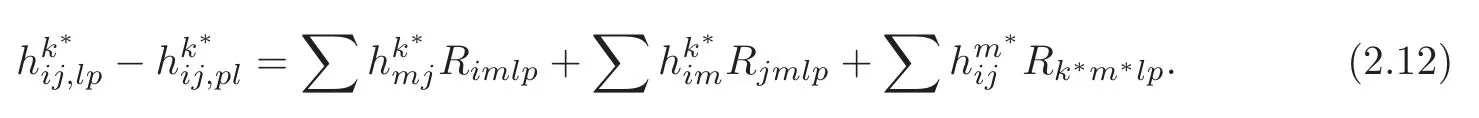
Note that,with respect to the adapted Lagrangian frame {ei,ei∗},the connection formsθi∗j∗=θij.It follows that

Furthermore,the first and second derivatives,of the mean curvature vector fieldHare given as

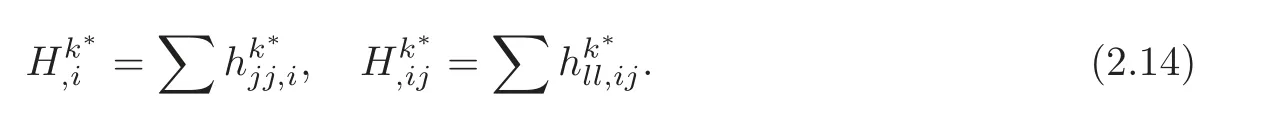
For any smooth functionfonMm,the covariant derivativesf,i,f,ijoff,the Laplacian offare respectively defined as follows:

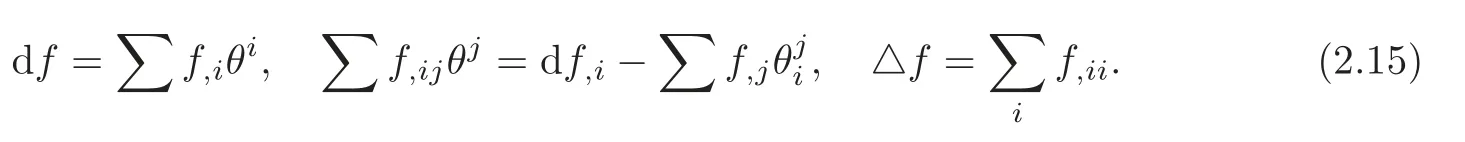
The well-known operator L acting on smooth functions is defined by (see [10])

which has been proven to be one of the most effect tools in the study of self-shrinkers and,more generally,ofλ-hypersurfaces.

3 Proof of Main Theorem

Letx:Mm→Cmbe a Lagrangianξ-submanifold.Then,with respect to an orthonormal frame field {ei},the defining equation (1.2) is equivalent to

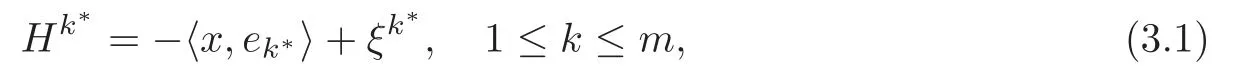
Lemma 3.1(see [13])Let x:M2→C2be a Lagrangian ξ-submanifold.Then

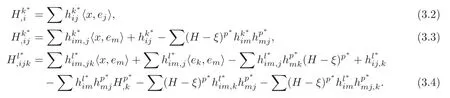
The following two lemmas are also obtained by direct computations,see also [15].

Lemma 3.2(see [15])Let K be the Gauss curvature of the induce metric on M2via x.Then it holds that

Lemma 3.3(see [15])It holds that

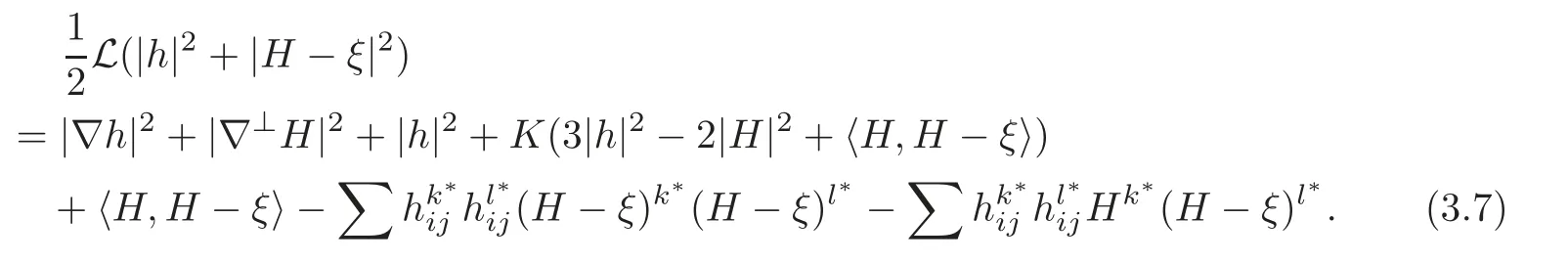
The following two propositions are important in the proof of Theorem 1.3,which are also key to the argument in [15].

Proposition 3.1(see [15])Let x:M2→C2be an oriented and compact Lagrangian ξ-submanifold.If

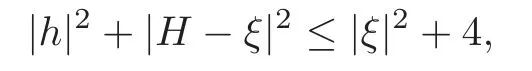
then

and x(M2)is a topological torus.

Proposition 3.2(see [15])Let x:Mm→Nmbe a Lagrangian submanifold in a K¨ahler manifold Nmwith the second fundamental form h.If both Mmand Nmare flat,then around each point p∈Mm,there exists an orthonormal frame field{ei,ei∗}with ei∗=Jei(1≤i≤m)such that,at the point p,

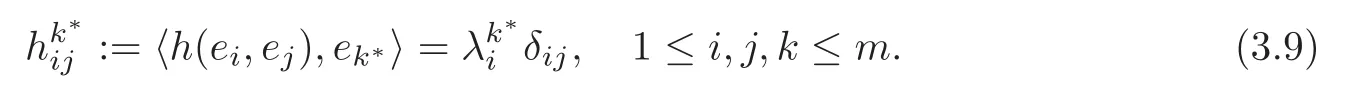
Now we are in the position to give the proof of Theorem 1.3.

Firstly,by Proposition 3.1,

So,with respect to any local orthonormal frame field {e1,e2},it holds that

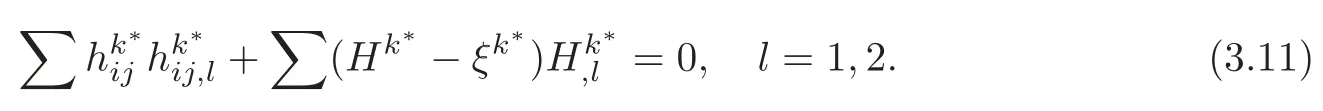
Secondly,it is much more convenient for us to simply consider the following two cases.

Case 1:ξ=0.

In this case,Theorem 1.3 reduces to Corollary 1.1.

Case 2:ξ≠0.

In this case,we easily find that the normal bundleT⊥M2has an orthonormal parallel frame field{e3,e4},say,we can takee3to be parallel toξ.It follows that the immersionx:M2→C2is of flat normal bundle.Sincexis Lagrangian,its tangent bundleT M2must also be flat(i.e.K≡0) because the complex structureJ:T M2→T⊥Mis a bundle isomorphism which preserves both the bundle metric and the bundle connection.Then it follows from the Gauss equation that |h|2≡|H|2.Consequently,for any local orthonormal frame field {ei,ei∗},we have |h|2i≡|H|2i,i=1,2,and L(|h|2)=L(|H|2).Equivalently,

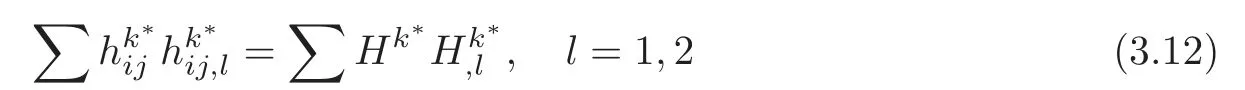
and

by (3.5)–(3.6) and the fact that

To proceed,we need to prove the following proposition.

Proposition 3.3Let x:M2→C2be a flat Lagrangian ξ-submanifold inC2.Then for any orthonormal frame field{e1,e2},we have

ProofSincexis flat and Lagrangian,the normal bundleT⊥M2is also flat.So by (2.2),(2.11) and Ricci identities,∇rhis totally symmetric for anyr≥0.It then follows from (3.4)that

Thus Proposition 3.3 is proved.

Now,from (3.11) and (3.12) we find

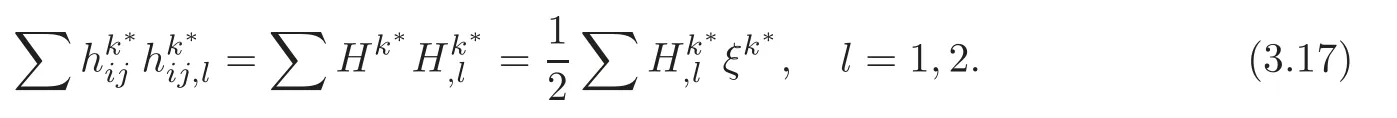
Next we are to prove thathis parallel,i.e.,∇h≡0.For this end we first assume the contrary.Then |∇h|2must be positive at some point onM2.Letp∈M2be the point such that

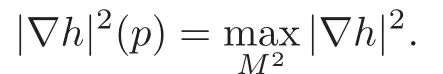
Then we have that |∇h|2(p)>0 and

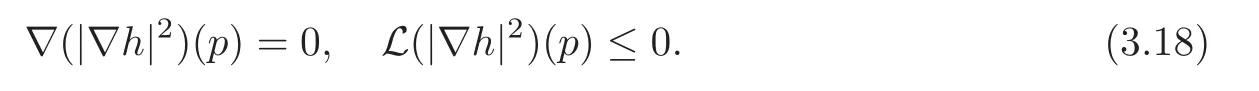
Furthermore,by Proposition 3.2,we can choose an orthonormal frame field {ei,ei∗} such that

Sinceis totally symmetric ini,j,k,we know that

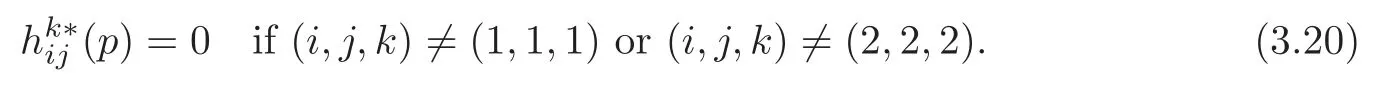
This with (3.2) shows that

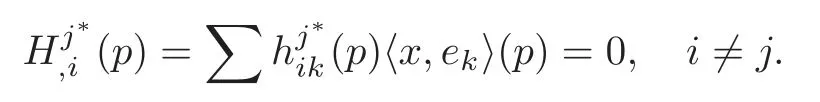
Therefore

atp.

On the other hand,from (3.12),(3.17) and (3.20),we obtain atp

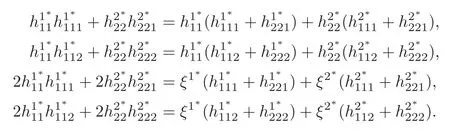
It then follows from (2.11) and (3.21) that,atp,

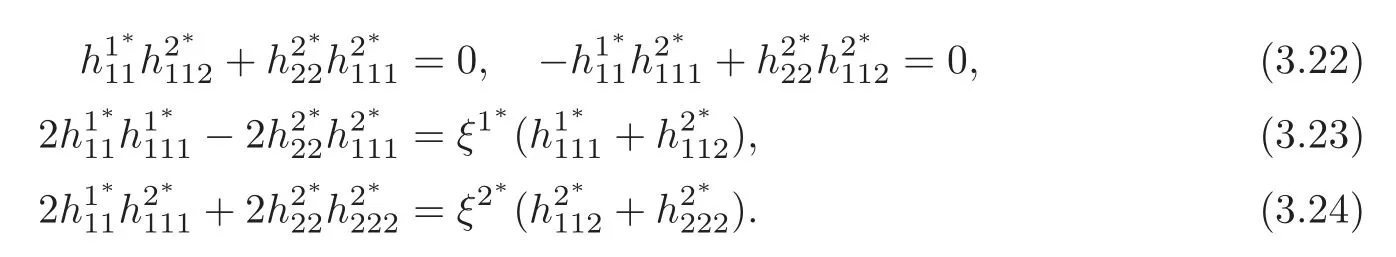
Noting that

due to (3.10),we find from (2.11) and (3.21)–(3.22) that atp,

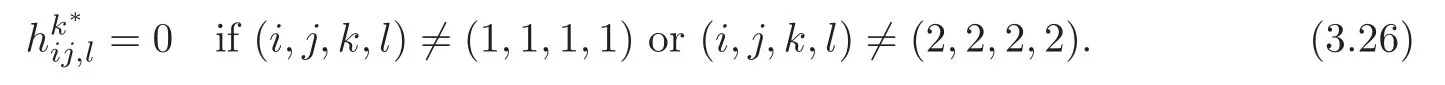
It follows that

Inputting (3.26) into (3.23) and (3.24),we obtain atp,

Without loss of generality,by the contrary assumption we can assume that(p)≠0.Then from (3.28) we have

We need to consider the following two cases separately:

(1)(p)≠0.

In this case,we also have

Thus

and thusH(p)−ξ(p)=It follows that

which contradicts to (3.10).

(2)(p)=0.

In this case,we have

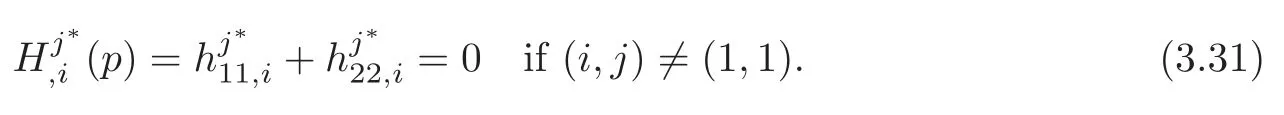
On the other hand,from (3.7),(3.10) and (3.13)–(3.14),we find

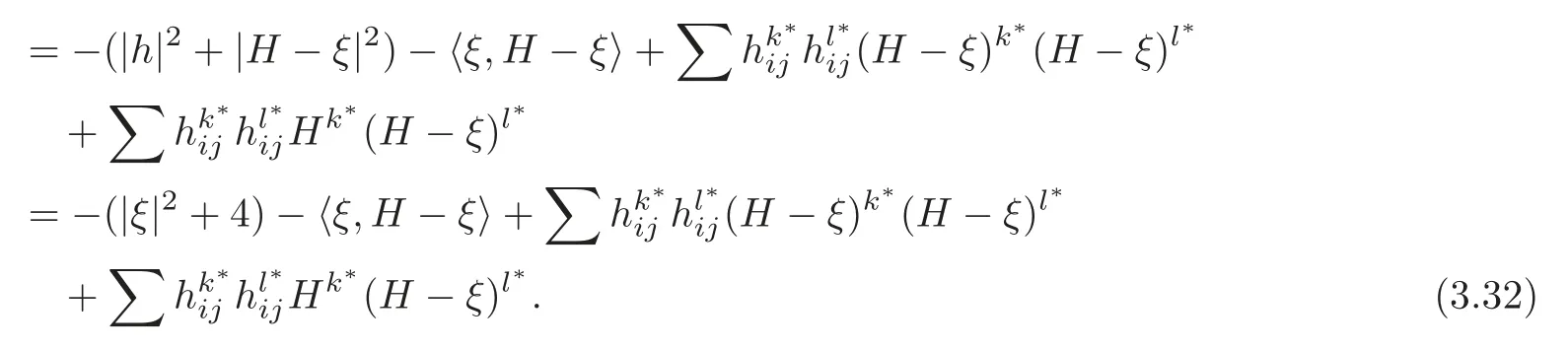
Thus,using (3.32),we directly find

Inserting (3.18),(3.26)–(3.27),(3.29) and (3.31) into (3.33),we obtain that

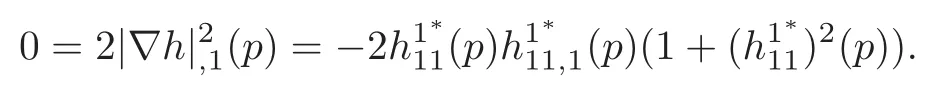
So thatξ1∗(p)=(p)=0.This with (3.17),(3.26),(3.31),Proposition 3.3 and the assumption that(p)=0 shows that

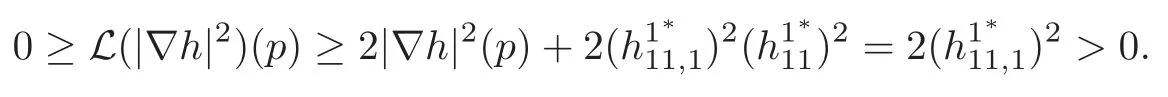
This contradiction shows that ∇h≡0.

SinceM2is flat,it is locally isometric to R2.Therefore,the fact that ∇h≡0 and (3.19)guarantee that,each pointp∈M2has an open neighbourhoodUpon which a parallel orthonormal frame field {e1,e2} is defined such that the corresponding componentssatisfy

onUp.Moreover,are all constant.

Now let

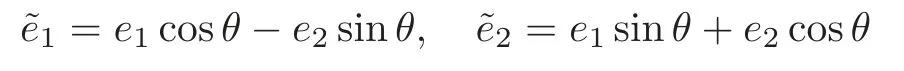
be another oriented frame field such that the corresponding componentsalso satisfy (3.34).Then a direct computation shows that we obtain

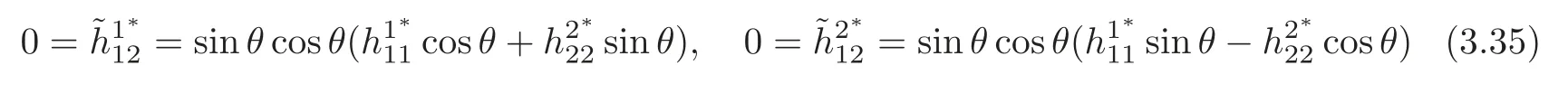
and

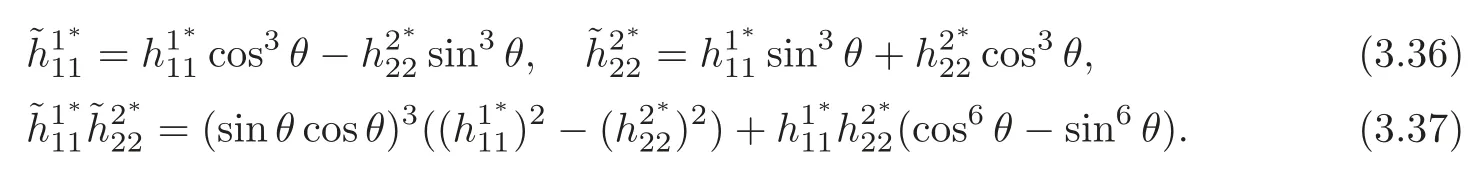
Let {ω1,ω2} be the dual frame of {e1,e2}.Then we have

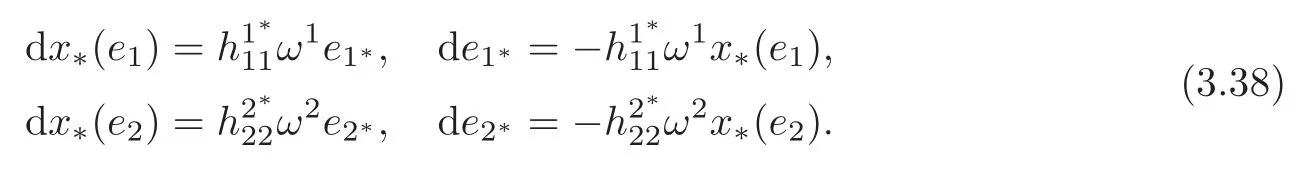
We claim that>0.In fact,if=0,thenx∗(e2) is a constant vector in C2alongM2which means thatx(M) contains a family of parallel straight lines,contradicting to the compactness ofM.

Define

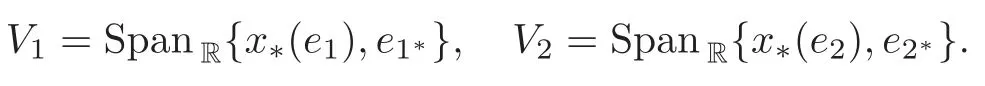
Then (3.38) shows thatV1,V2are two orthogonal and constant complex line bundles onM2,corresponding to two orthogonal,one dimensional complex subspaces of C2.So,up to some holomorphic isometry of C2,we can identify bothV1andV2with C1. Due to the flatness ofM2,the isometric immersionxcan be locally represented byx≡(γ1,γ2):(a1,b1)×(a2,b2)→C1×C1≡C2,where

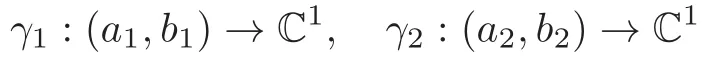
are two unit-speed curves (i.e.,with arc-length parameters).Moreover,as plane curves,the curvatures ofγ1andγ2are respectively the constants>0 and>0.So bothγ1(a1,b1)andγ2(a2,b2) are circle arcs of radiusa:=()−1andb:=()−1,respectively.

Finally,by the compactness ofM2,we obtain thatx(M2)=S1(a)×S1(b).Therefore,Theorem 1.3 is proved.

Proof of Theorem 1.4:

Case(1):ξ=0.In this case,the theorem reduces to the theorem of Li and Wang(Theorem 1.1).

Case (2):ξ≠0.In this case,(3.14) still holds and thus the inequality |h|2−〈H,ξ〉≤2 is equivalent to that |h|2+|H−ξ|2≤|ξ|2+4.Therefore,Theorem 1.4 is equivalent to Theorem 1.3 in the present case.

AcknowledgementThe authors would like to thank the reviewer’s careful revisions and suggestions,which are helpful for improving our manuscript.