Critical Trace Trudinger-Moser Inequalities on a Compact Riemann Surface with Smooth Boundary∗
2022-07-08MengjieZHANG
Mengjie ZHANG
1School of Mathematics,Renmin University of China,Beijing 100872,China.E-mail: zhangmengjie@ruc.edu.cn
Abstract In this paper,the author concerns two trace Trudinger-Moser inequalities and obtains the corresponding extremal functions on a compact Riemann surface (Σ,g) with smooth boundary ∂Σ.Explicitly,let
and
where W1,2(Σ,g)denotes the usual Sobolev space and ∇g stands for the gradient operator.By the method of blow-up analysis,we obtain
Moreover,the author proves the above supremum is attained by a function uα ∈H∩C∞(Σ)for any 0≤α <λ1(∂Σ).Further,he extends the result to the case of higher order eigenvalues.The results generalize those of[Li,Y.and Liu,P.,Moser-Trudinger inequality on the boundary of compact Riemannian surface,Math.Z.,250,2005,363–386],[Yang,Y.,Moser-Trudinger trace inequalities on a compact Riemannian surface with boundary,Pacific J.Math.,227,2006,177–200]and [Yang,Y.,Extremal functions for Trudinger-Moser inequalities of Adimurthi-Druet type in dimension two,J.Diff.Eq.,258,2015,3161–3193].
Keywords Trudinger-Moser inequality,Riemann surface,Blow-up analysis,Extremal function
1 Introduction
Let Ω ⊆R2be a smooth bounded domain and(Ω) be the completion ofC∞0(Ω) under the Sobolev normwhere ∇R2is the gradient operator on R2and‖·‖2denotes the standardL2-norm.The classical Trudinger-Moser inequality (see [20,24–25,27,32]),as the limit case of the Sobolev embedding,says

Moreover,4πis the best constant for this inequality in the sense that whenβ >4π,all integrals in (1.1) are finite and the supremum is infinite.It is interesting to know whether or not the supremum in(1.1)can be attained.For this topic,see Carleson-Chang[5],Flucher[11],Lin[17],Adimurthi-Struwe [2],Li [13–14],Zhu [38],Tintarev [26],Zhang [33–34,37]and the references therein.
Trudinger-Moser inequalities were studied on Riemann manifolds by Aubin [3],Cherrier[6],Fontana [12]and others.In particular,let (Σ,g) be a compact Riemann surface with smooth boundary∂Σ andW1,2(Σ,g) be the completion ofC∞(Σ) under the norm
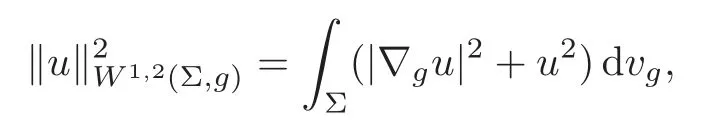
where ∇gandvgstand for the gradient operator and the volume element on Σ with respect to the metricg,respectively.Liu [18]derived a trace Trudinger-Moser inequality in his doctoral thesis from the result of Osgood-Phillips-Sarnak [23]: For all functionsu∈W1,2(Σ,g),there holds some constantCdepending only on (Σ,g) such that
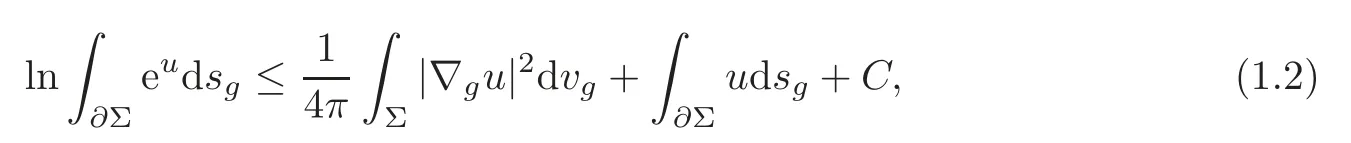
wheresgdenotes the induced length element on∂Σ with respect tog.Later Li-Liu[15]obtained a strong version of (1.2),namely
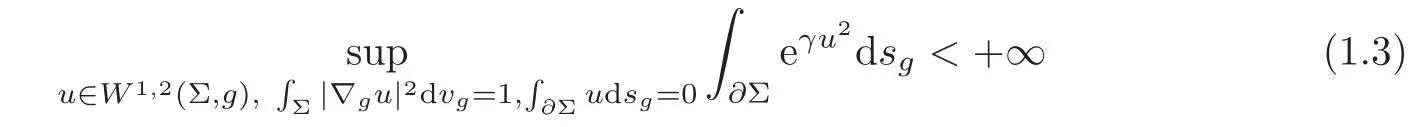
for anyγ≤π.This inequality is sharp in the sense that all integrals in (1.3) are finite whenγ >πand the supremum is infinite.Moreover,for anyγ≤π,the supremum is attained.After that,Yang [28]established the boundary estimate without direct boundary conditions,which is
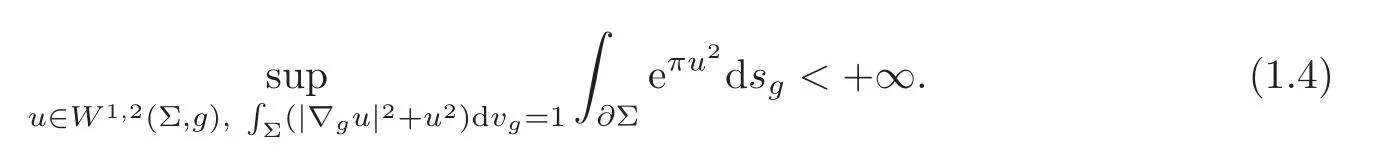
Moreover,the supremum in (1.4) can be attained.
A different form was also derived by Yang [30],namely
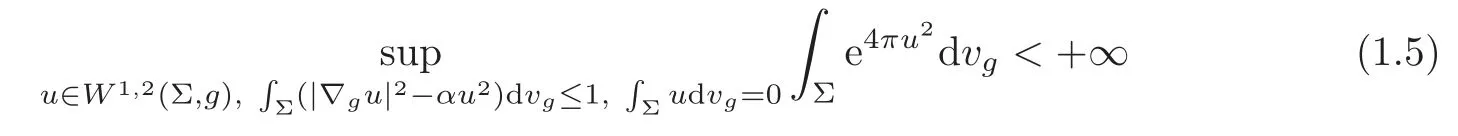
for all 0≤α<λ1(Σ),where

is the first eigenvalue of the Laplace-Beltrami operator ∆g.Further,he extended (1.5) to the case of higher order eigenvalues.Precisely,letλ1(Σ)<λ2(Σ)<···be all distinct eigenvalues of the Laplace-Beltrami operator andEλk(Σ)={u∈W1,2(Σ,g):∆gu=λk(Σ)u},k=1,2,···be associated eigenfunction spaces.For any positive integerk,we set

and

Then we have

for all 0≤α <λk(Σ);moreover the above supremum can be attained by some functionuα∈E⊥k(Σ).
In this paper,we will establish two new trace Trudinger-Moser inequalities,which are extensions of (1.5) and (1.6),respectively.Precisely we first have the following theorem.
Theorem 1.1Let(Σ,g)be a compact Riemann surface with smooth boundary ∂Σ,λ1(∂Σ)be defined as
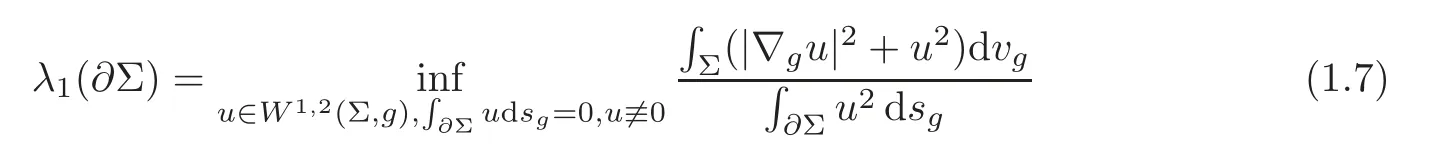
and
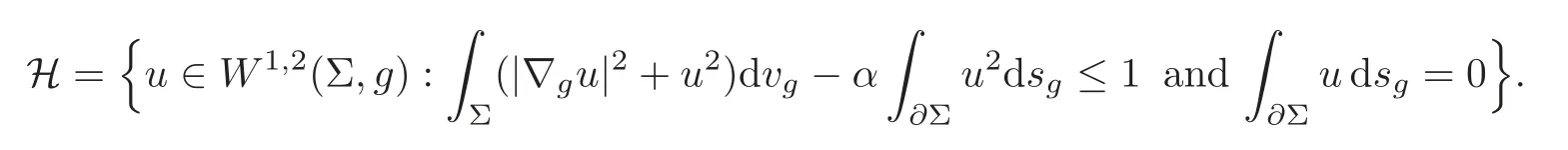
Then we have
(i)when0≤α<λ1(∂Σ),we have

and it can be attained by some function uα∈H ∩C∞(Σ);
(ii)when α≥λ1(∂Σ),the above supremum is infinite.
An interesting consequence of Theorem 1.1 is the following weak form of (1.8).
Theorem 1.2Let(Σ,g)be a compact Riemann surface with smooth boundary ∂Σ,λ1(∂Σ)be defined as in(1.7).Then for any0≤α <λ1(∂Σ),u∈W1,2(Σ,g)andudsg=0,thereexists a constant C >0depending only on α and(Σ,g),such that

Moreover,we extend Theorem 1.1 to the case of higher order eigenvalues.Let us introduce some notations.For any positive integerk,we set

where n denotes the outward unit normal vector on∂Σ and
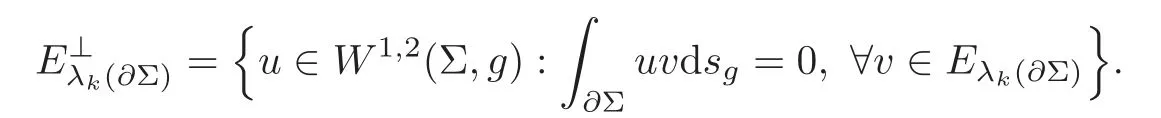
Then we set
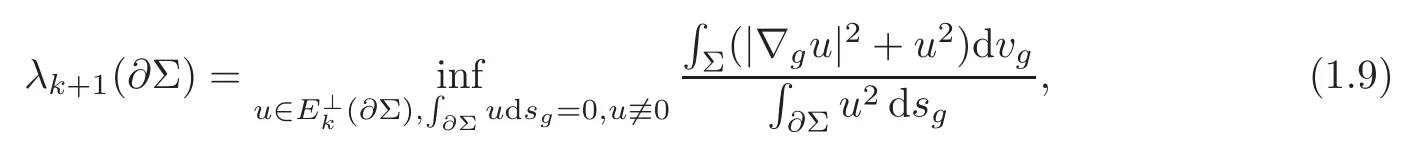
which is the (k+1)-th eigenvalue of ∆gon∂Σ,where
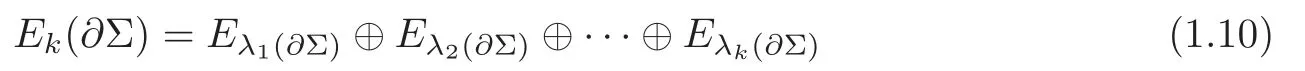
and
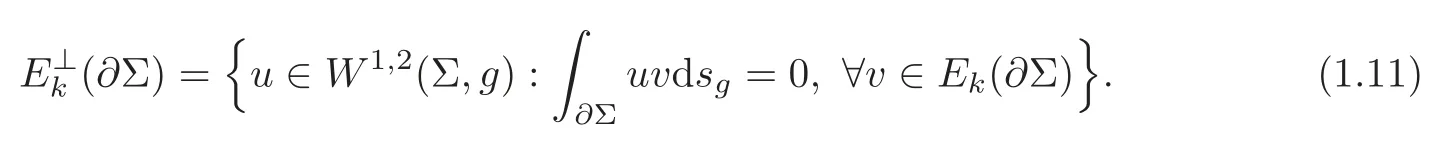
We note thatW1,2(Σ,g)=Ek(∂Σ)⊕E⊥k(∂Σ).Then a generalization of Theorem 1.1 can be stated as follows.
Theorem 1.3Let(Σ,g)be a compact Riemann surface with smooth boundary ∂Σand λk+1(∂Σ)be defined by(1.9).For any0≤α<λk+1(∂Σ),let
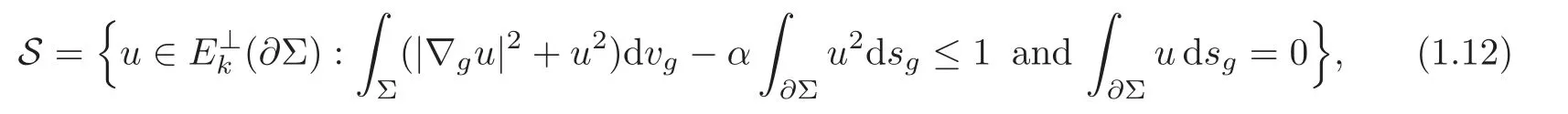
where E⊥k(∂Σ)is defined as in(1.11).Then the supremum

is attained by some function uα∈S ∩C∞().
Clearly Theorems 1.1 and 1.3 extend (1.5) and (1.6) to the trace Trudinger-Moser inequalities,respectively.For theirs proofs,we employ the method of blow-up analysis,which was originally used by Carleson-Chang [5],Ding-Jost-Li-Wang [8],Adimurthi-Struwe [2],Li [13],Liu [18],Li-Liu [15]and Yang [28–29].This method is now standard.For related works,we refer Adimurthi-Druet [1],do ´O-de Souza [7,9],Nguyen [21–22],Zhu [39],Fang-Zhang [10],Mancini-Martinazzi [19]and Zhang [35–36].
In the remaining part of this paper,we prove Theorem 1.1 in Section 2 and Theorem 1.3 in Section 3,respectively.
2 The First Eigenvalue Case
In this section,we will prove Theorem 1.1(ii) first,and then we will prove Theorem 1.1(i).Without loss of generality,we do not distinguish sequence and subsequence in the following.
2.1 The case of α≥λ1(∂Σ)
Letλ1(∂Σ) be defined in (1.7).It is easy to know thatλ1(∂Σ) is attained by some functionu0∈W1,2(Σ,g)satisfyingBy a direct calculation,we derive thatu0satisfies the Euler-Lagrange equation
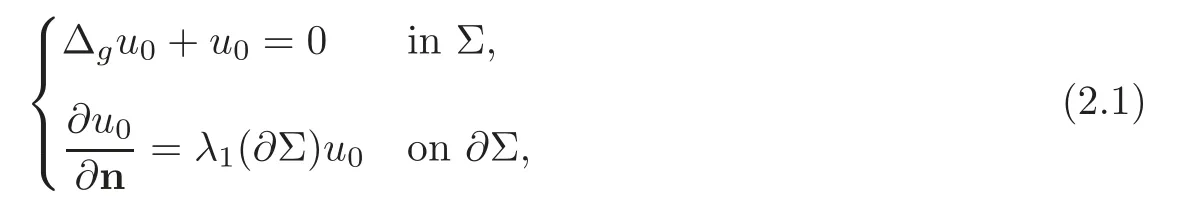
where ∆gdenotes the Laplace-Beltrami operator,n denotes the outward unit normal vector on∂Σ.Applying elliptic estimates to (2.1),we haveu0∈W1,2(Σ,g)∩C0().Then we obtain thatλ1(∂Σ)can be attained by some functiontu0∈W1,2(Σ,g)∩C0(Σ)for any positive integert.
Sinceα≥λ1(∂Σ),we have
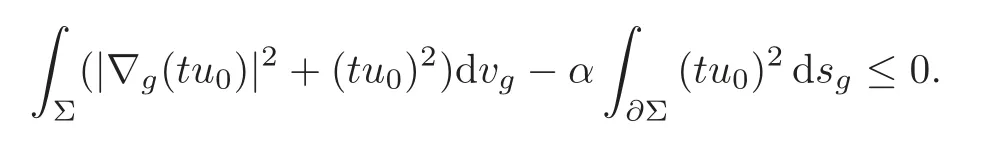
Then there holdstu0∈H ∩C0().In view ofu00,we obtain that there is a pointx0∈∂Σ withu0(x0)>0.Moreover,there exists a neighborhood U ofx0satisfyingu0(x)≥>0 in U.Then we get

Lettingt→+∞,one has Theorem 1.1(ii).
2.2 The case of 0≤α <λ1(∂Σ)
In this subsection,we will prove Theorem 1.1(i)by four steps: Firstly,we consider the existence of maximizers for subcritical functionals and the corresponding Euler-Lagrange equation;secondly,we deal with the asymptotic behavior of the maximizers through blow-up analysis;thirdly,we deduce an upper bound of the supremumunder the assumption that blow-up occurs;finally,we construct a sequence of functions to show that Theorem 1.1(i)holds.
Step 1Existence of maximizers for subcritical functionals.For any 0≤α<λ1(∂Σ),we let
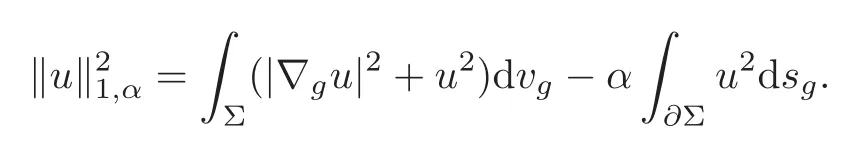
We have the following lemma.
Lemma 2.1For any0<ε <π,the supremumis attained by somefunction uε∈H ∩C∞().
ProofLet 0<ε<πbe fixed.By the definition of supremum,we can choose a maximizing sequencein H such that
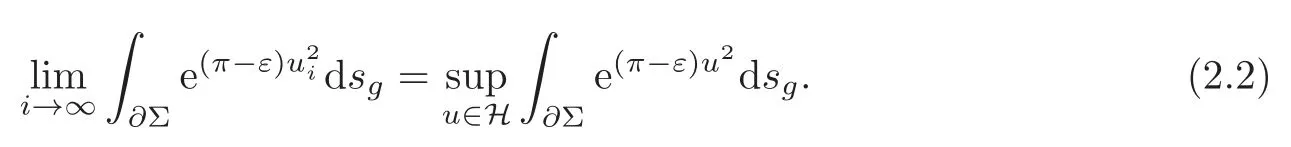
Moreover,uiconverges to some functionuεweakly inW1,2(Σ,g) and strongly inLp(∂Σ,g) for anyp >1.Then we haveAccording to the definition of weak convergence and the Hölder’s inequality,we getwhich gives ‖uε‖≤1.From Lagrange’s mean value theorem,the Hölder’s inequality and (1.3),there holds

In view of (2.2),we have

Suppose ‖uε‖<1,then one gets
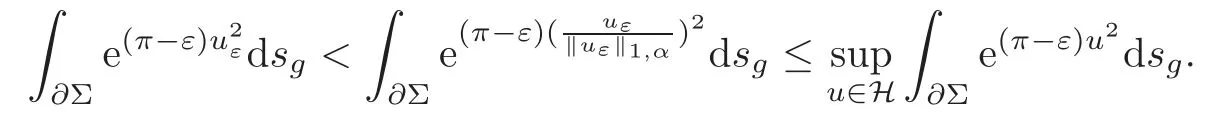
This result contradicts with (2.3).Hence ‖uε‖=1 holds anduε∈H.
By a direct calculation,we derive thatuεsatisfies the Euler-Lagrange equation
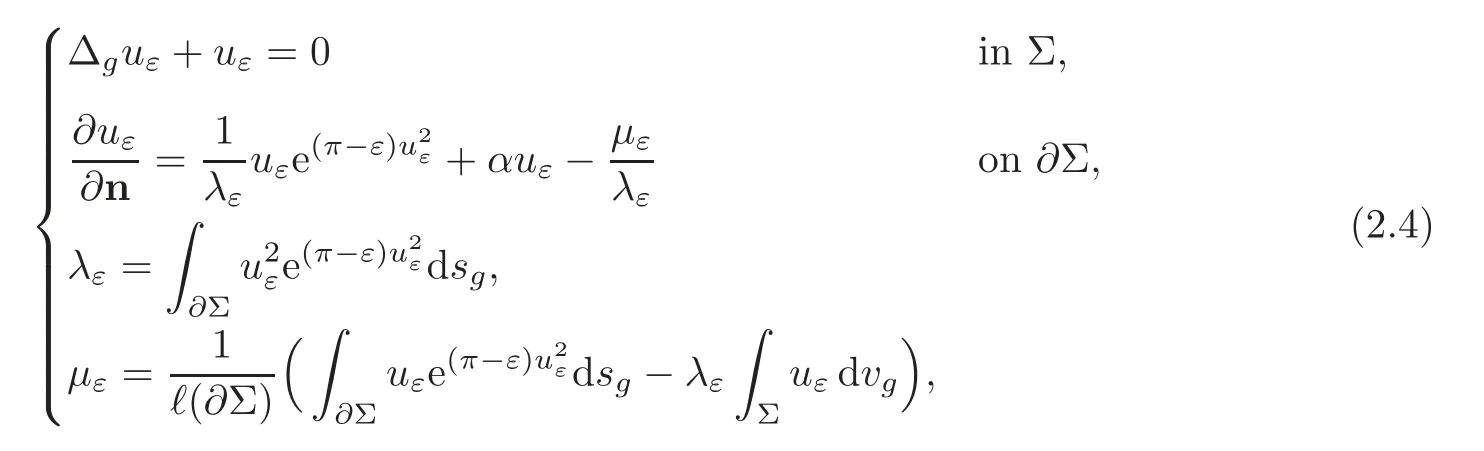
whereℓ(∂Σ) denotes the length of∂Σ.Applying elliptic estimates to (2.4),we haveuε∈H ∩C∞().Then Lemma 2.1 follows.
Moreover,we have
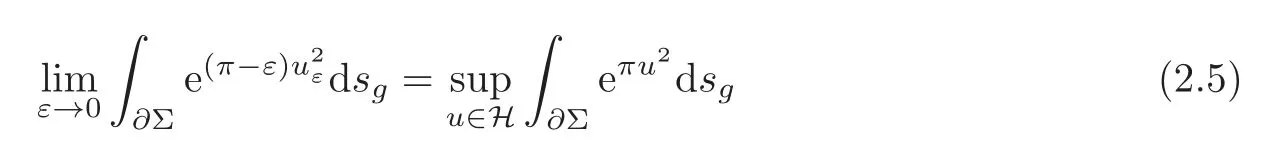
from Lebesgue’s dominated convergence theorem.It follows from(2.5)and the fact of et≤1+tetfor anyt≥0 that

From (2.6) anduε∈H,one gets
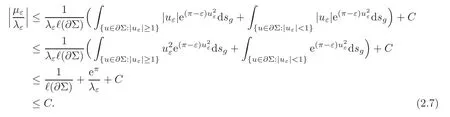
Step 2Blow-up analysis.
Let us perform the blow-up analysis.Without loss of generality,we setcε=|uε(xε)|=Ifcεis bounded,by elliptic estimates,we complete the proof of Theorem 1.1(i).In the following,we assumeandxε→pasε→0.Applying maximum principle to (2.4),we havep∈∂Σ.Then we have the following lemma.
Lemma 2.2There hold uε0weakly in W1,2(Σ,g)and uε→0strongly in L2(∂Σ,g)as ε→0.Furthermore,|∇guε|2dvgpin sense of measure,where δpis the usual Dirac measure centered at p.
ProofSinceuεis bounded inW1,2(Σ,g),there exists some functionu0such thatuε⇀u0weakly inW1,2(Σ,g)anduε→u0strongly inL2(∂Σ,g)asε→0.Then we haveand ‖u0‖≤1.
Supposeu00,then one hasand
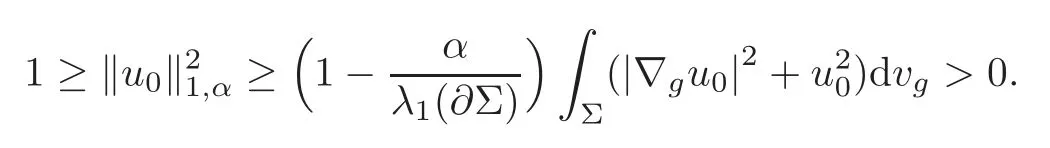
Then we obtain ‖∇g(uε−u0)‖22→1−‖u0‖asε→0.Lettingζ=1−‖u0‖,one has 0≤ζ <1.For sufficiently smallε,there holds

From the Hölder’s inequality,(1.3) and (2.8),we get e(π−ε)u2εis bounded inLq(∂Σ,g) for sufficiently smallε.Applying the elliptic estimate to(2.4),one gets thatuεis uniformly bounded,which contradictscε→+∞.That is to sayu0≡0.
Suppose |∇guε|2dvg⇀µ≠δpin sense of measure.Then there exists some positive numberr>0 such thatwhereBr(p)is a geodesic ball centered atpwith radiusr.Moreover,we obtainfor sufficiently smallε.We choose a cut-offfunctionρ∈C10(Br(p)),which is equal to 1 infor sufficiently smallε.Hence there holds

for someq >1.In view of (1.3),we obtainis bounded inLq(Br2(p)∩∂Σ,g) for sufficiently smallε.Applying the elliptic estimate to(2.4),we get thatuεis uniformly bounded inBr4(p)∩∂Σ,which contradictscε→+∞.Therefore,Lemma 2.2 follows.
Now we analyse the asymptotic behavior ofuεnear the concentration pointp.Let

Following[31,Lemma 4],we can take an isothermal coordinate system(U,φ)nearx0,such thatφ(x0)=0,φ(U)=B+randφ(U∩∂Σ)=∂R2+∩Brfor some fixedr >0,where B+r={(x1,x2)∈R2:x21+x22≤r2,x2>0} and R2+={x=(x1,x2) ∈R2:x2>0}.In such coordinates,the metricghas the representationg=e2f(dx21+dx22) andfis a smooth function withf(0)=0.Denote=uε◦φ−1,=φ(xε) andUε={x∈R2:+rεx∈φ(U)}.Define two blowing up functions inUε,

and

In view of (2.4) and (2.9)–(2.11),for any fixedR>0,we obtain

and
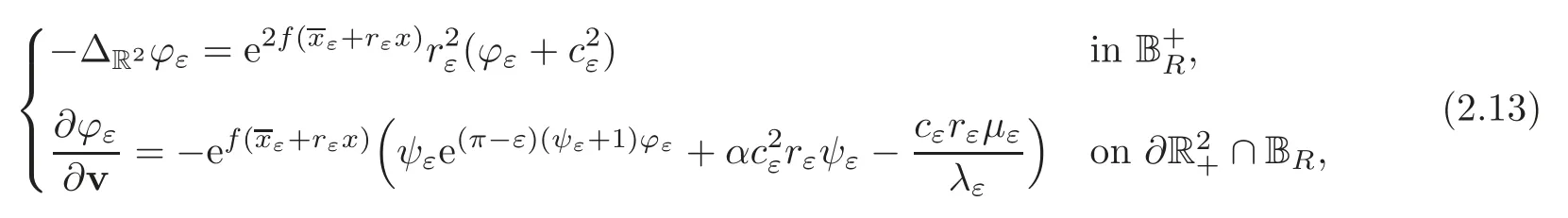
where ∆R2denotes the Laplace operator on R2,v denotes the outward unit normal vector on∂R2+,Br={x∈R2: dist(x,0)≤r} and B+r={x=(x1,x2) ∈Br:x2>0} for anyr >0.Applying elliptic estimates to (2.12),we havefor any fixedR >0 withψ(0)=1.According to (2.4),(2.7) and (2.9),we getThen there holds

Using the same argument for (2.13) as above,we obtain

whereϕsatisfies
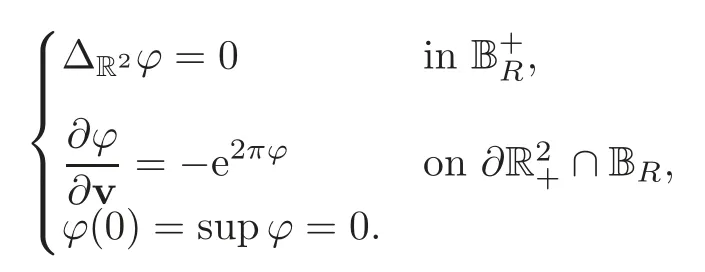
It is not difficult to check that
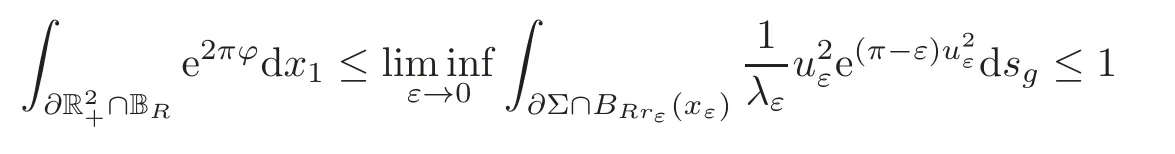
for any fixedR>0,that is to sayBy a result of Li-Zhu [16],we obtain

A direct calculation gives

Next we discuss the convergence behavior ofuεaway fromp.Denoteuε,β=min{βcε,uε}∈W1,2(Σ,g) for any real number 0<β <1.Following [29,Lemma 4.7],we can easily get

Lemma 2.3Letting λεbe defined by(2.4),we obtain

and

ProofRecalling (2.4) and (2.18),one gets
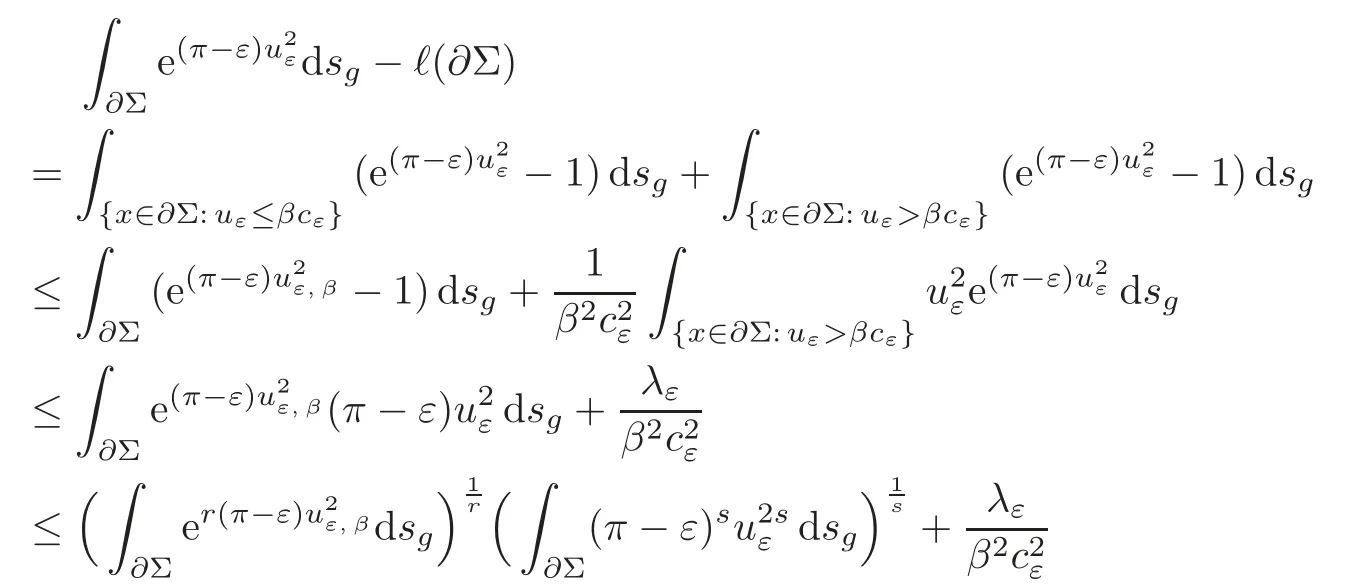
for any real number 0<β <1 and somer,s >1 withFrom (1.3) and (2.18),is bounded inLr(∂Σ,g).Lettingε→0 first and thenβ→1,we obtain
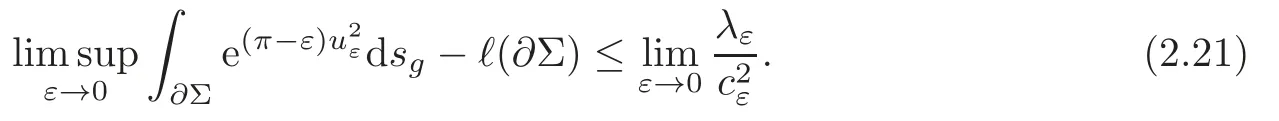
According tocε=(2.4) and Lemma 2.2,we have
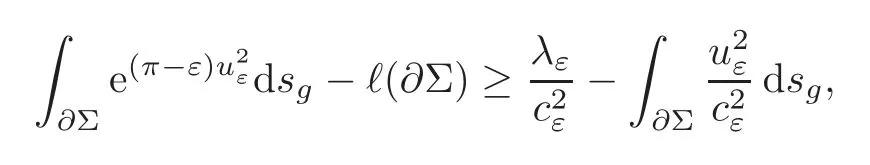
that is to say
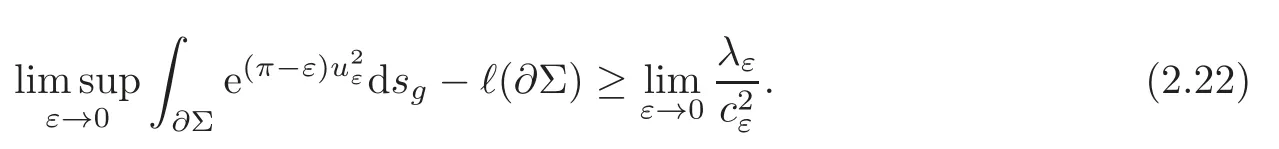
Combining (2.21) with (2.22),one gets (2.19).
Applying (2.4) and (2.9)–(2.11),we have
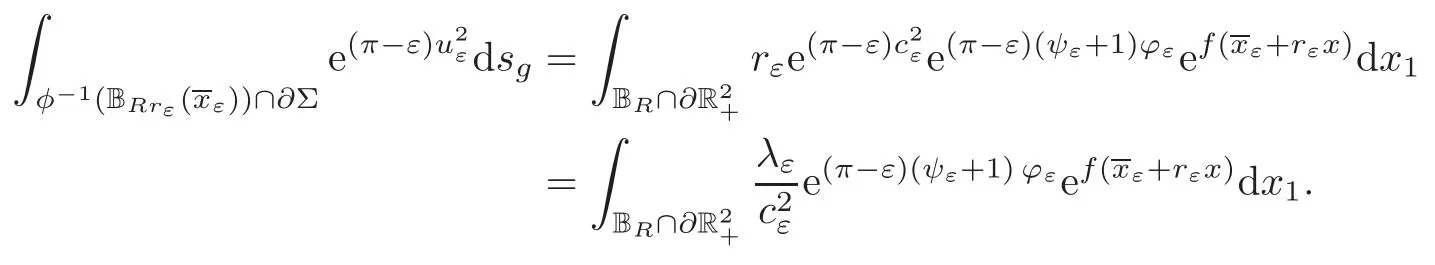
From (2.14)–(2.17),(2.20) holds.
Next we consider the properties ofcεuε.Combining Lemma 2.3 with [29,Lemma 4.9],we obtain

Furthermore,one has the follwing lemma.
Lemma 2.4There hold
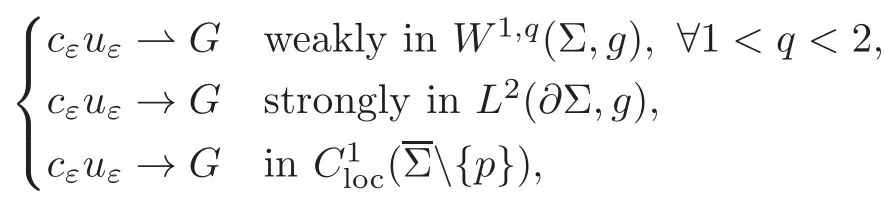
where G is a Green function satisfying

ProofFrom (2.4),there hold

Combining (2.4) with (2.23),we obtain
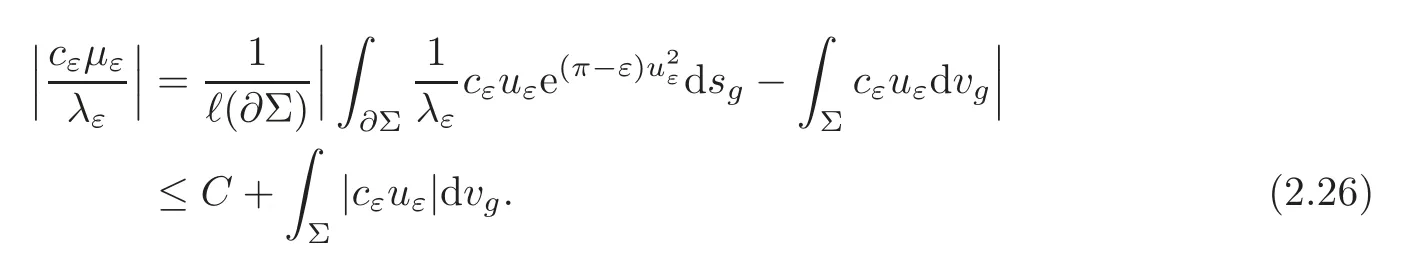
Moreover,it follows from the Poincar´e inequality that
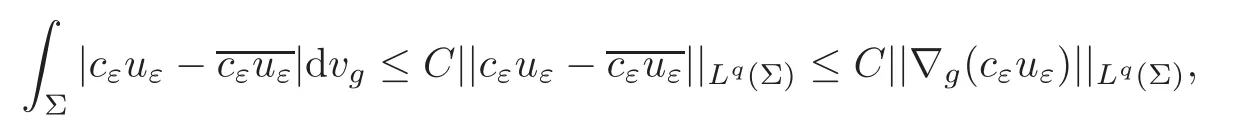

From the Hölder’s inequality and the Sobolev embedding theorem,one gets
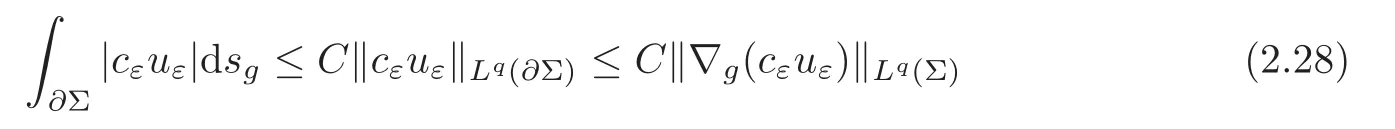
for someq >1.It is well known (see for example [15,Proposition 3.5]) that
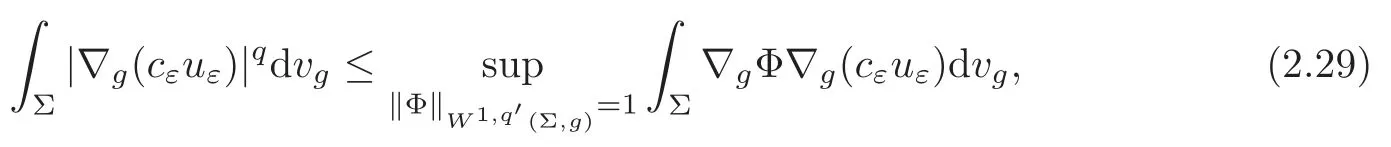
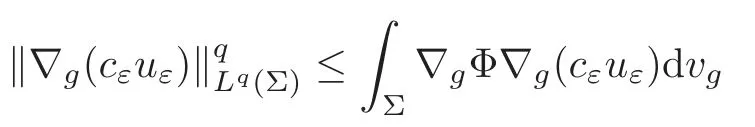

That is to say ‖∇g(cεuε)‖Lq(Σ)≤C.The Poincar´e inequality implies thatcεuεis bounded inW1,q(Σ,g) for any 1 For any fixedδ >0,we choose a cut-offfunctionη∈C∞() such thatη≡0 onBδ(p) andUsing Lemma 2.2,we haveHenceis bounded infor anys >1.It follows from (2.25) thatfor somes0>2. Applying the elliptic estimate to (2.25),we get thatcεuεis bounded inThen there holdsThis completes the proof of the lemma. Applying the elliptic estimate to (2.24),we can decomposeGnearp, wherer=dist(x,p) andApis a constant depending only onα,pand (Σ,g). Step 3Upper bound estimate. Lemma 2.5Under the hypotheses cε→+∞and xε→p∈∂Σas ε→0,there holds ProofWe take an isothermal coordinate system (U,φ) nearpsuch thatφ(p)=0,φmapsUto R2+,andφ(U∩∂Σ) ⊂∂R2+.In such coordinates,the metricghas the representationg=e2f(dx21+dx22) andfis a smooth function withf(0)=0.We claim that To confirm this claim,we setfor sufficiently smallδ >0 and some fixedR >0,whereIt follows from (2.30) and Lemma 2.4 that onwhich leads to whereoδ(1)→0,oε(1)→0 asε→0.According to (2.15)–(2.16),we have on∂BRrε∩R2+, then there holds From a direct computation,there holds Define and Recalling (2.4) and (2.9),we have Letting∈Wa,bandu∗ε=max{a,min{b,}},one getsfor sufficiently smallε.Further using ‖uε‖=1,we obtain Hence we have by Lemma 2.4, According to (2.11),(2.15) and (2.16),one gets whereoR(1)→0 asR→+∞.In view of (2.33)–(2.38),we obtain whereo(1)→0 asε→0 first,thenR→+∞andδ→0.Hence (2.32) follows.Combining(2.5),(2.32) with Lemma 2.3,we finish the proof of the lemma. Step 4Existence result. In this step,we always assume that 0≤α <λ1(∂Σ).We take an isothermal coordinate system (U,φ) nearpsuch thatφ(p)=0,φmapsUto R2+,andφ(U∩∂Σ) ⊂∂R2+.In such coordinates,the metricghas the representationg=andfis a smooth function withf(0)=0.Set a cut-offfunctionwithξ=1 onandDenoteβ=G+lnr−Apfor anyr >0,whereGis defined by (2.30).LetR=ln2ε,thenR→+∞andRε→0 asε→0.We construct a blow-up sequence of functions for some constantsB,cto be determined later,such that A delicate calculation shows and In view of (2.40)–(2.44),there holds Moreover,in order to assure thatvε∈W1,2(Σ,g),we obtain which is equivalent to According to (2.45)–(2.46),one gets It follows that in∂Σ ∩BRε(p), Hence On the other hand,from the fact et≥t+1 for anyt>0 and (2.39),we get From (2.47)–(2.48)andR=ln2ε,there holds for sufficiently smallε>0.The contradiction between (2.31)and (2.49)indicates thatcεmust be bounded.Then Theorem 1.1 follows. In this section,we will prove Theorem 1.3 involving higher order eigenvalues through blowup analysis.Letkbe a positive integer andEk(∂Σ)be defined by(1.10).Denote the dimension ofEk(∂Σ)bysk.From[4,Theorem 9.31],it is known thatskis a finite constant only depending onk.Then we can find a set of normal orthogonal basisofEk(∂Σ) satisfying wherek0≤kis a positive integer. Letλk+1(∂Σ)and S be defined by (1.9)and (1.12),respectively.In view of Lemma 2.1 and(3.1),we have the following lemma. Lemma 3.1Let0≤α<λk+1(∂Σ)be fixed.For any0<ε<π,the supremum is attained by some function uε∈S ∩C∞(Σ).Moreover,the Euler-Lagrange equation of uεis Without loss of generality,we setcε=|uε(xε)|=We first assume thatcεis bounded,which together with elliptic estimates completes the proof of Theorem 1.3.In the remainder of Section 3,we assume andxε→pasε→0.Applying maximum principle to (3.2),we havep∈∂Σ.Similar to Lemma 4,we get the following lemma. Lemma 3.2There hold cεuε⇀G weakly in W1,q(Σ,g) (∀1 Moreover,Gnearpcan be decomposed into wherer=dist(x,p) andApis a constant depending only onα,pand (Σ,g).Analogous to Lemma 2.5,using the capacity estimate,we derive an upper bound of the supremum (1.13): We always assume thatcε→+∞asε→0.Take an isothermal coordinate system (U,φ)nearpsuch thatφ(p)=0,φmapsUto R2+,andφ(U∩∂Σ) ⊂∂R2+.In such coordinates,the metricghas the representationg=e2f(dx21+dx22) andfis a smooth function withf(0)=0.Set a cut-offfunctionξ∈withandDenoteβ=G+lnr−Ap,whereGis defined by (3.3).LetR=ln2ε,thenR→+∞andRε→0 asε→0.We construct a blow-up sequence of functions for some constantsB,cto be determined later,such that andvε−∈S,whereAnalogous to Subsection 2.4,we determine the constants and Then we get Setting for sufficiently smallε >0.The contradiction between (3.4) and (3.6) indicates that the assumption of=+∞is not true.Thencεmust be bounded and Theorem 1.3 follows from the elliptic estimate.



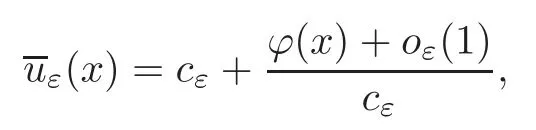
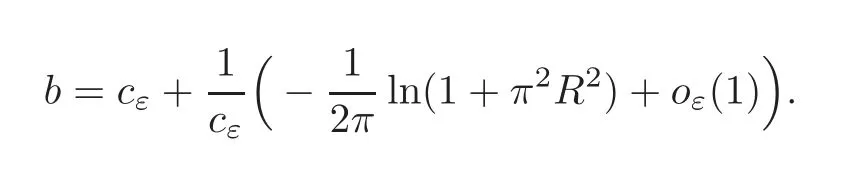
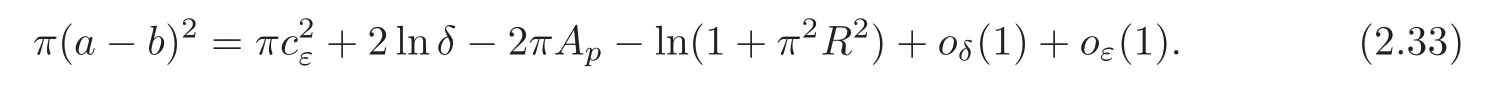
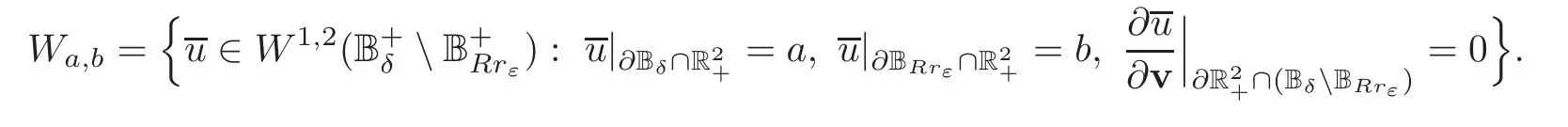

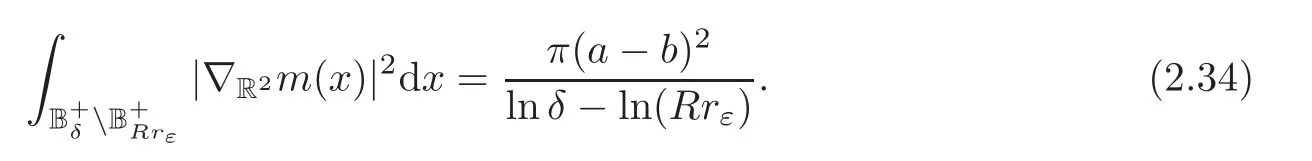


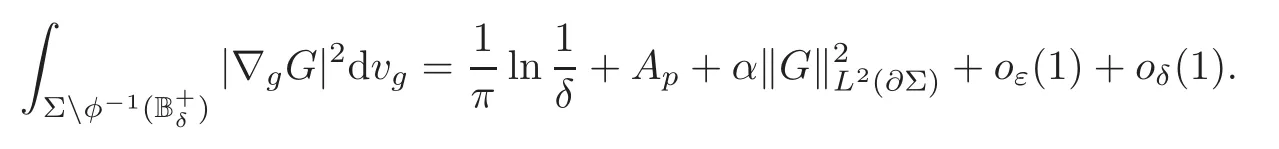
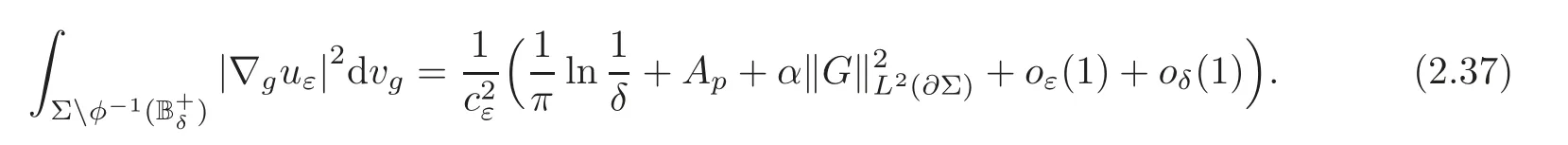



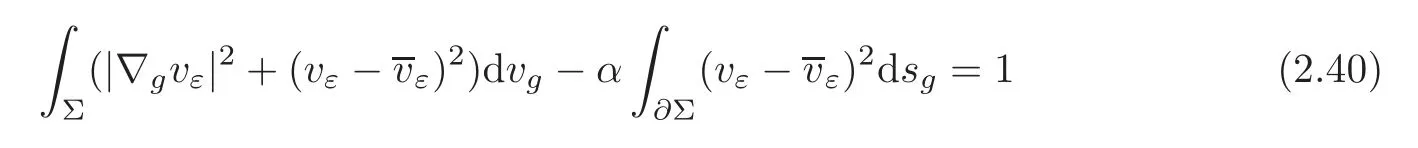
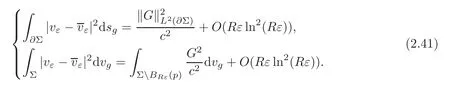


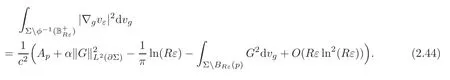

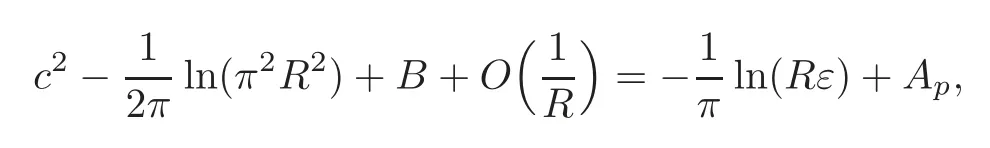

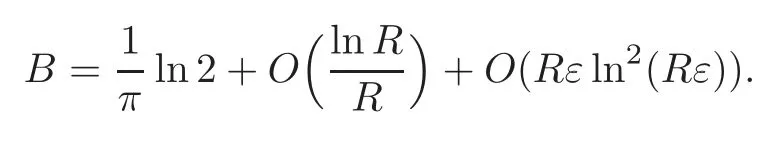

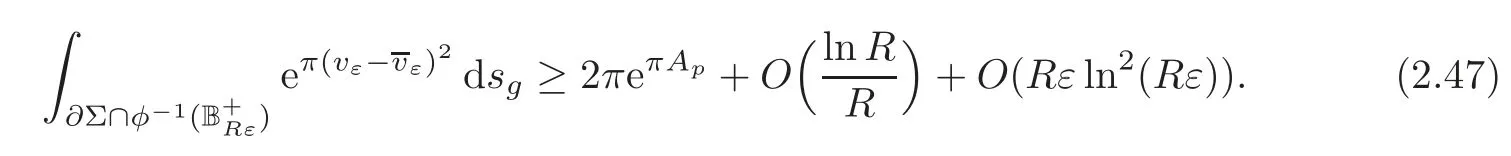


3 Higher Order Eigenvalue Cases

3.1 Blow-up analysis
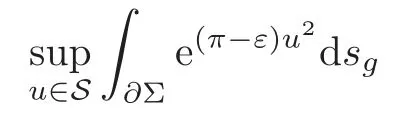


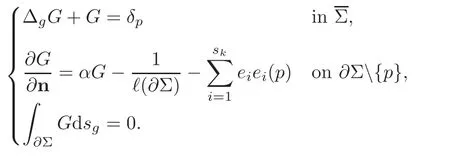


3.2 Existence result
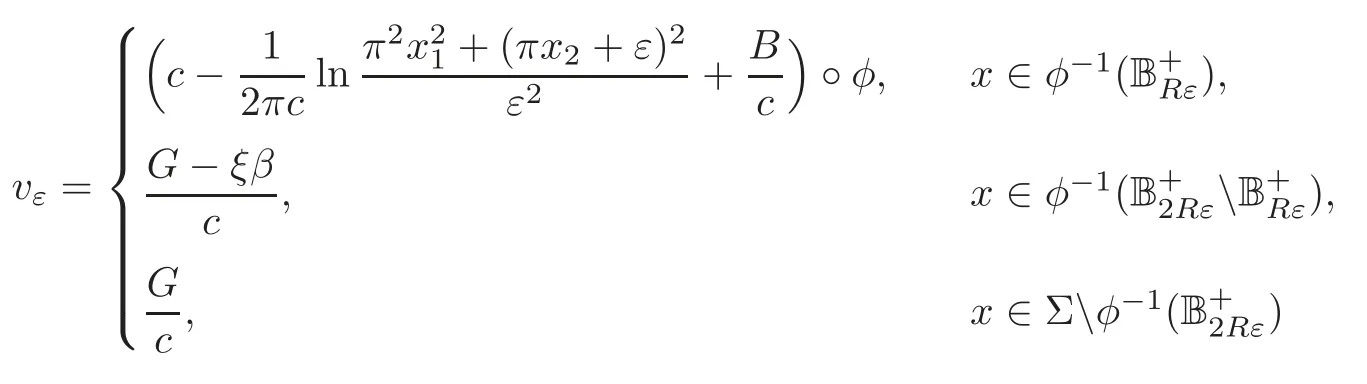

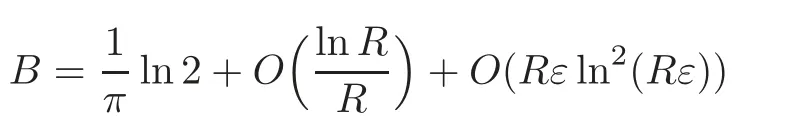
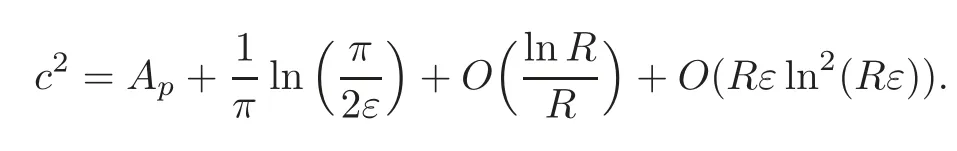
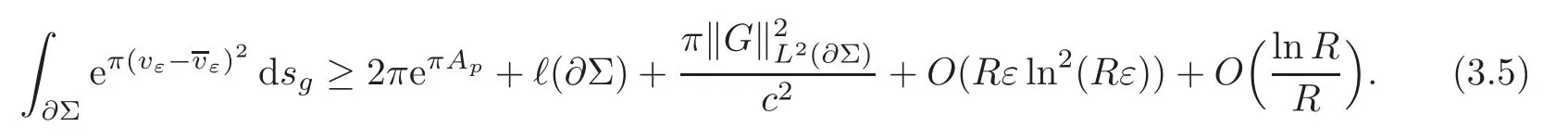
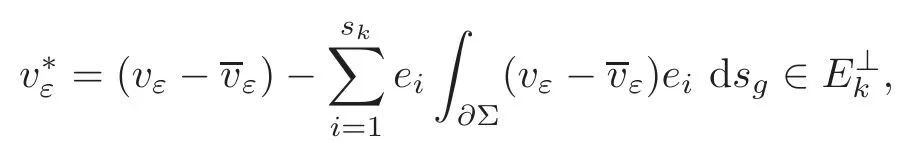
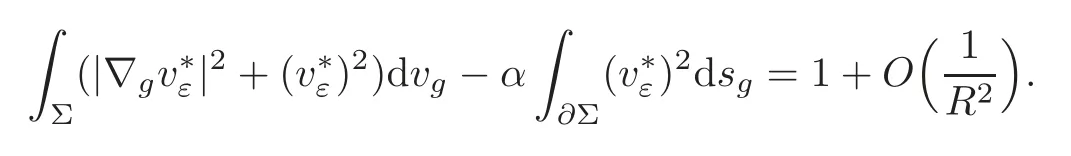

杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- A Characterization of the Standard Tori in C2 as Compact Lagrangian ξ-Submanifolds∗
- Four Families of Nontrivial Product Elements in the Stable Homotopy Groups of Spheres∗
- Canonical Connections and Algebraic Ricci Solitons of Three-dimensional Lorentzian Lie Groups∗
- On a Supercongruence Conjecture of Z.-W.Sun∗
- Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗
- Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗
