On a Supercongruence Conjecture of Z.-W.Sun∗
2022-07-08GuoshuaiMAO
Guo-shuai MAO
1Department of Mathematics,Nanjing University of Information Science and Technology,Nanjing 210044,China.E-mail: maogsmath@163.com
Abstract In this paper,the author partly proves a supercongruence conjectured by Z.-W.Sun in 2013.Let p be an odd prime and let a ∈Z+.Then,if p≡1 (mod 3),
is obtained,where()is the Jacobi symbol.
Keywords Supercongruences,Binomial coefficients,Fermat quotient,Jacobi symbol
1 Introduction
In the past years,congruences for sums of binomial coefficients have attracted the attention of many researchers (see,for instance,[1,3–4,6,10,12,16–17,19]).In 2011,Sun [17]proved that for any odd primepanda∈Z+,
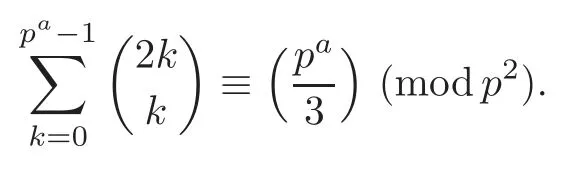
Recently,Liu and Petrov [7]showed some congruences on sums ofq-binomial coefficients.
Pan and Sun [13]proved that for any primep≡1 (mod 4) or 1 In 2017,Mao and Sun [11]showed that for any primep≡1 (mod 4) or 1 Sun [15]proved that for any odd primepanda∈Z+, In this paper,we partly prove Sun’s conjecture (see [15,Conjecture 1.2(i)]). Theorem 1.1Let p be an odd prime and let a∈Z+.If p≡1 (mod 3),then We shall prove Theorem 1.1 in Section 2.Our result is much interesting because of much rarer are the examples where the upper limit of the sum is strictly betweenandp−1,and these congruences are much more difficult to handle. Lemma 2.1(see [5])For any prime p>3,we have the following congruences modulo p Proof of Theorem 1.1In view of (1.1),we just need to verify that Letkandlbe positive integers withk+l=paand 0 and So we have It is easy to see that fork=1,2,···, This,with Fermat’s little theorem yields that Thus,by (2.1) we only need to show that Now we set then we only need to prove that Settingn=n−1 in the last equation of page 3 in [18],we have It is easy to check that for each 0≤k≤n−1−m, whereB(P,Q) stands for the beta function.It is well known that the beta function relates to gamma function: So Therefore Hence,by (2.6),we just need to show that It is obvious that where By the following transformation we have In view of [2,(1.48)],we have and it is easy to check that Thus Now we calculate C.First we have the following transformation Hence, With the help of package Sigma (see [14]),we find the following identity: which can be easily proved by induction onN. SubstitutingN=n−m−1,i=m+1−jinto the above identity,we have It is easy to check that Therefore Hence That is One can easily check that and (the following identity can be found in [2]) These yield that Replacingnbymin the above equation,we have Hence So In view of [16,(1.20)],and by (2.2)–(2.4) we have It is obvious that Sincep≡1 (mod 3),by [8,Lemma 17(2)],we have These,with (2.7)–(2.10) yield that we only need to prove the following congruence: There are only the items 3j+1=pa−1(3k+1) withk=0,1,···,so,by [9,Theorem 1.2]and Lucas congruence,we have Therefore the proof of Theorem 1.1 is complete. AcknowledgementThe author would like to thank the anonymous referees for helpful comments.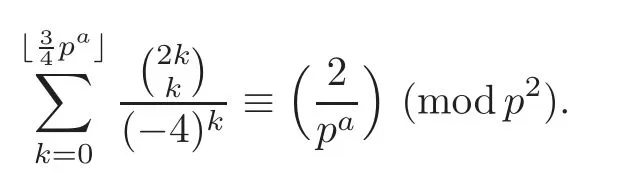
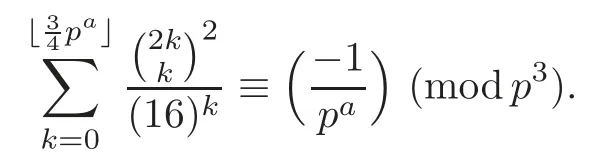

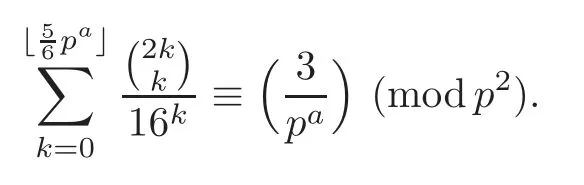
2 Proof of Theorem 1.1
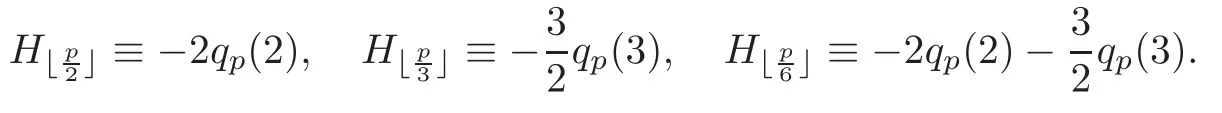






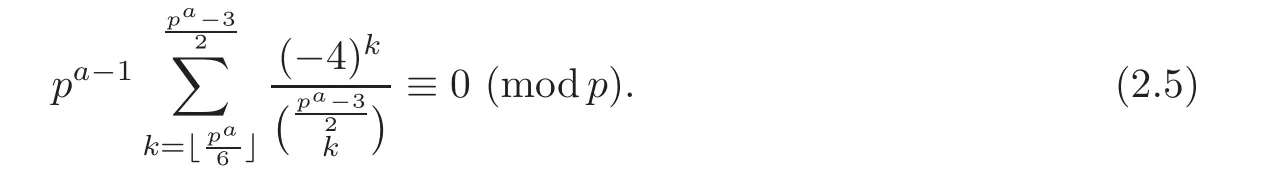
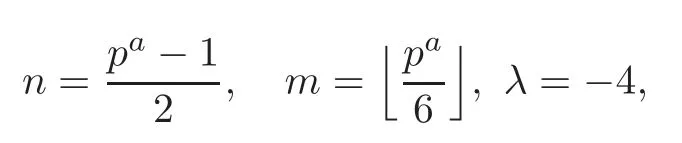

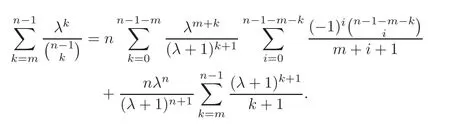
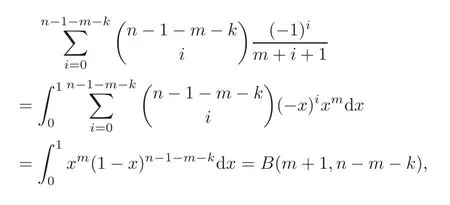
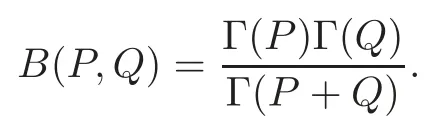



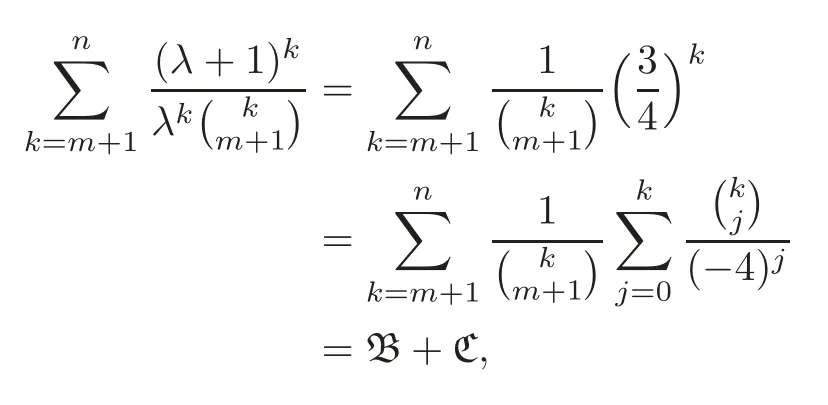
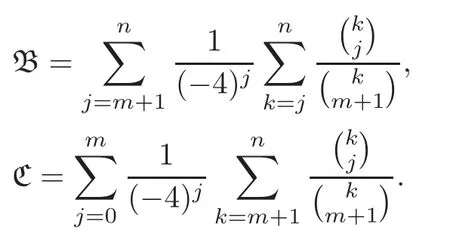

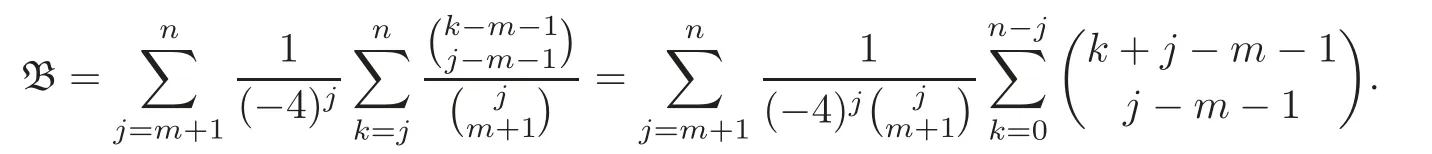

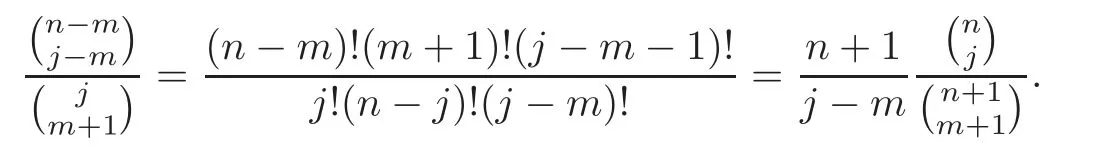

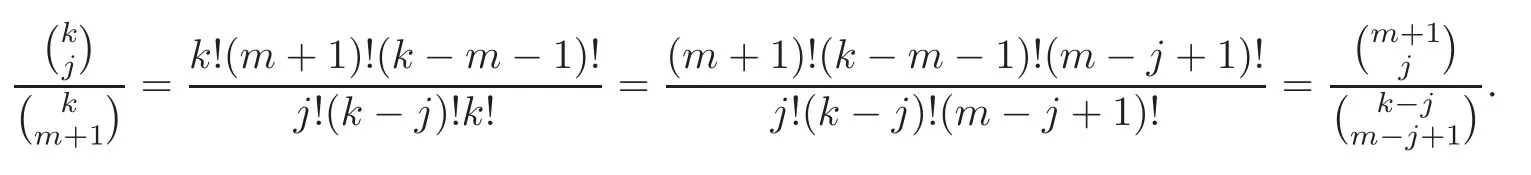
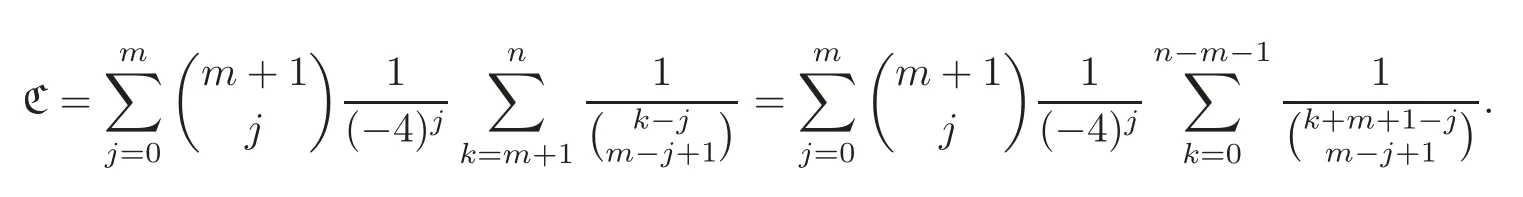
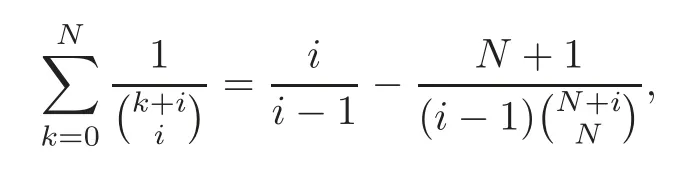
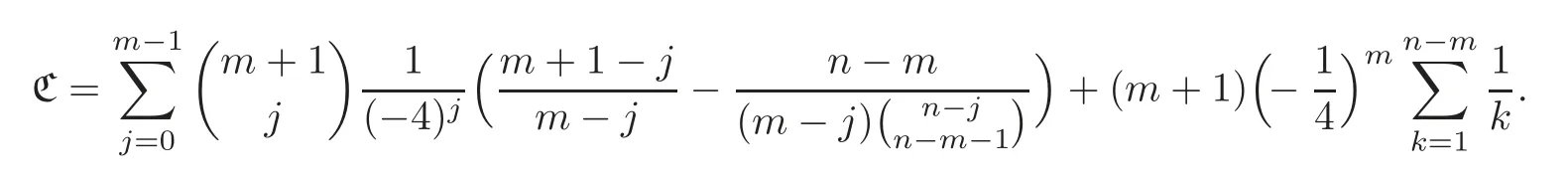



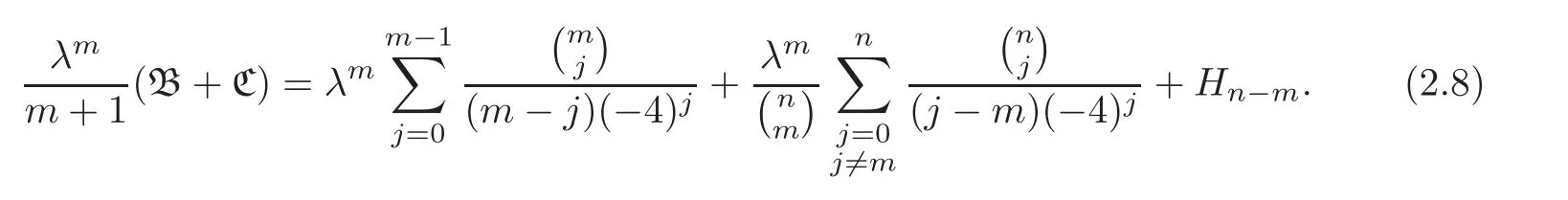

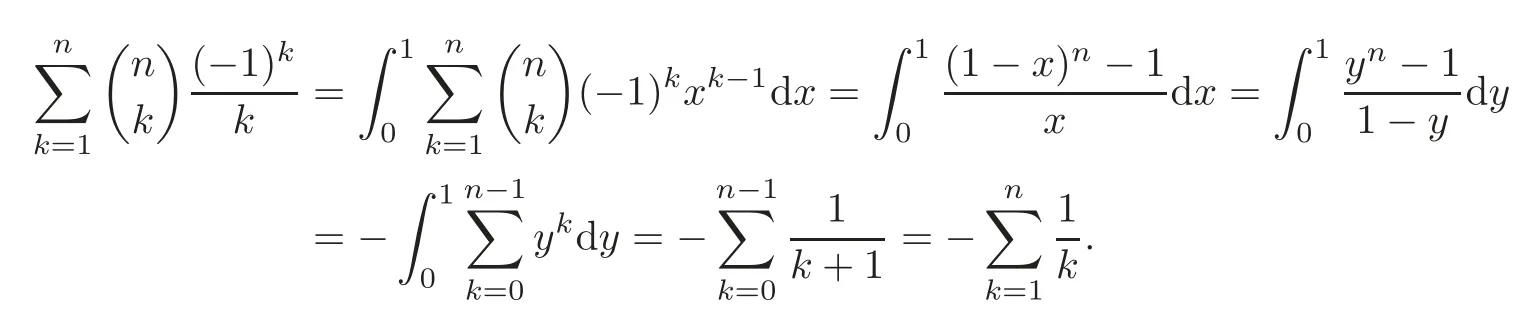
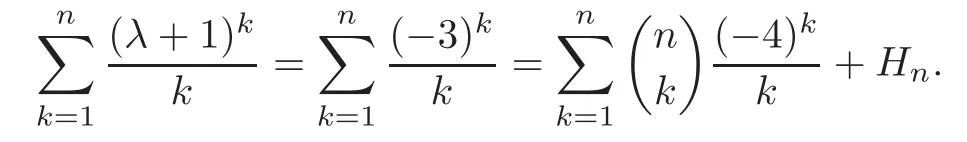
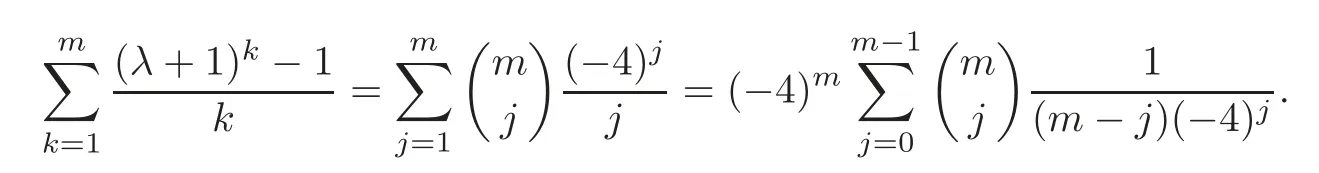


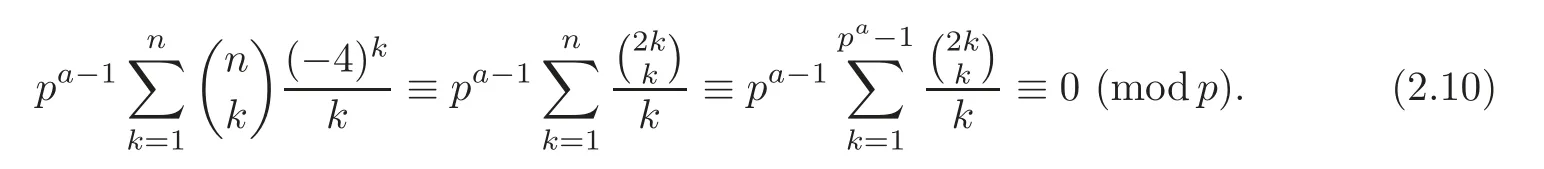
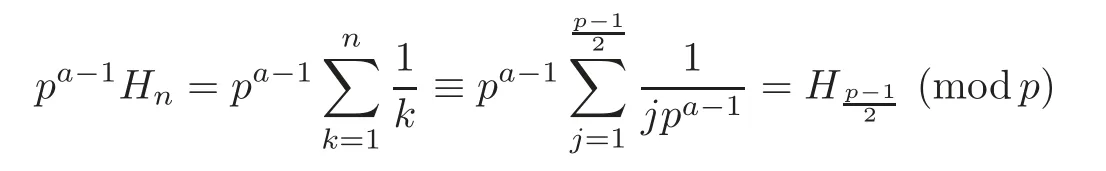
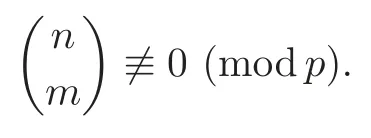
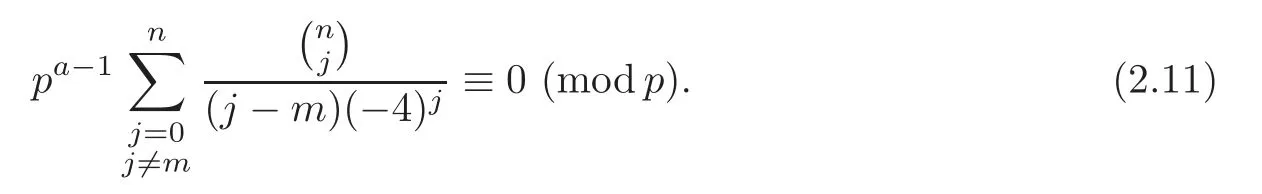
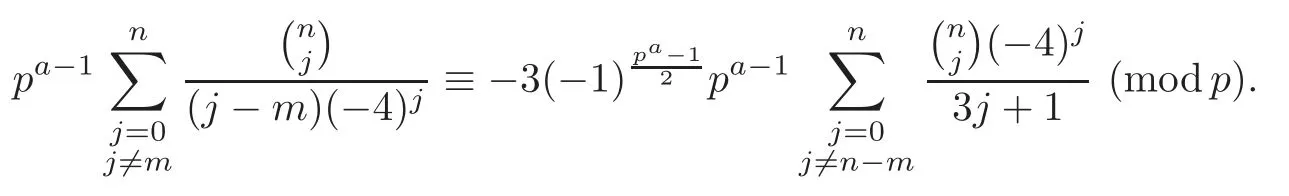
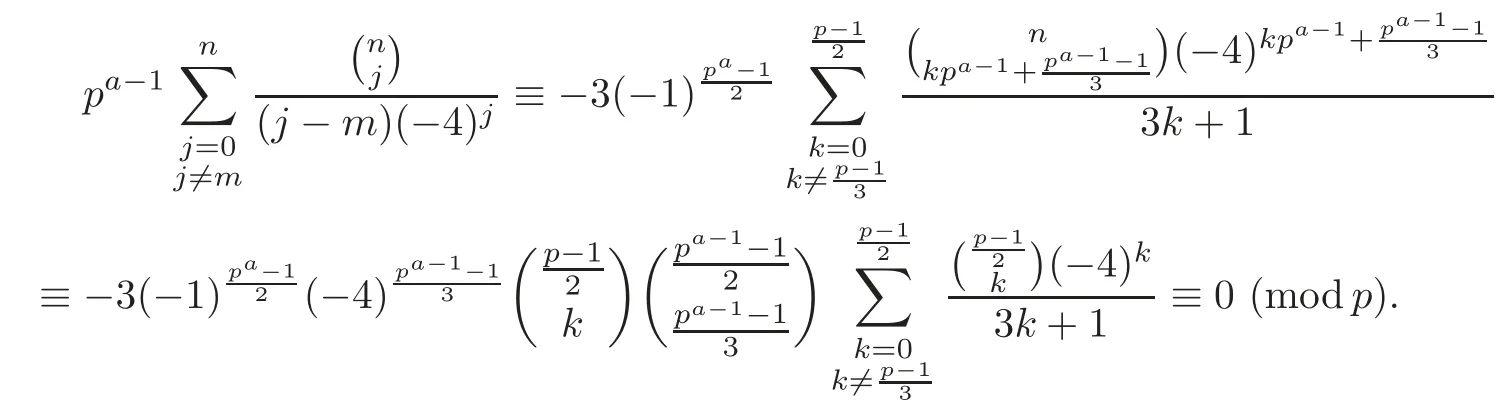
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Ground States of K-component Coupled Nonlinear Schrödinger Equations with Inverse-square Potential∗
- Rotational Hypersurfaces with Constant Gauss-Kronecker Curvature
- A Note on the Indirect Controls for a Coupled System of Wave Equations∗
- A Generalization of Lappan’s Theorem to Higher Dimensional Complex Projective Space∗
- Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗
- Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗
