Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗

Yiyuan ZHANG Guangfu CAO Li HE

1School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China.E-mail: yiyuanzhang@e.gzhu.edu.cn guangfucao@163.com

2Corresponding author.School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China.E-mail: helichangsha1986@163.com

Abstract In this paper,the authors investigate the boundedness of Toeplitz product TfTg and Hankel product H∗fHg on Fock-Sobolev space for f,g ∈P.As a result,the boundedness of Toeplitz operator Tf and Hankel operator Hf with f ∈P is characterized.

Keywords Toeplitz product,Hankel product,Fock-Sobolev space

1 Introduction

Let Cnbe the Euclidean space of complex dimensionnand dvbe the Lebesgue measure on Cn.Forz=(z1,···,zn) andw=(w1,···,wn) in Cn,we denote

The Fock spaceF2consists of all entire functionsfon Cnsuch that

Let N be the set of nonnegative integers.For any multi-indexα=(α1,···,αn) ∈Nnandz∈Cn,we write

where∂jdenotes the partial derivative with respect to thezj.

For anym∈N,the Fock-Sobolev spaceF2,mconsists of all entire functionsfon Cnsuch that

The Fock-Sobolev space was introduced by Cho and Zhu in [4],where they proved thatf∈F2,mif and only if the functionzαf(z)is inF2for all multi-indexesαwith |α|=m,which allows us to introduce the equivalent norm onF2,m:

where

is a normalizing constant such that the constant function 1 has norm 1 inF2,m.

For anyz∈Cn,Let

DenoteL2mby the space of Lebesgue measurable functionsfon Cnso that the functionf(z) ∈L2(Cn,dVm).It is well-known that the spaceL2mis a Hilbert space with the inner product

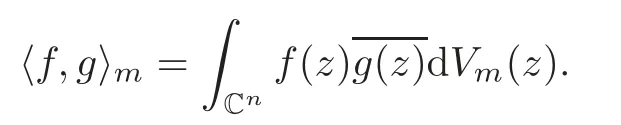
It is clear that the Fock-Sobolev spaceF2,mis a closed subspace ofL2m.LetPmbe the orthogonal projection fromL2mtoF2,m,that is

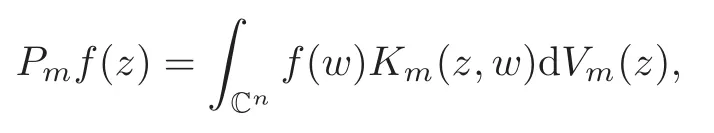
whereKm(z,w) is the reproducing kernel ofF2,m.

For a Lebesgue measurable functionfon Cnsuch thatfKm(z,·)are inL2(Cn,dVm)for allz∈Cn,the Toeplitz operator with symbolfonF2,mis defined by

and the Hankel operatorHfwith symbolfis given by

whereIis the identity operator onL2m.

The original Toeplitz product problem was raised by Sarason in [8],to ask whether one can give a characterization for the pairs of outer functionsg,hin the Hardy spaceH2such that the operatoris bounded onH2.The famous Sarason’s conjecture on this problem has attracted the attention of some mathematical researchers in operator theory.This problem was partially solved on the Hardy space of the unit circle in [13],on the Bergman space of the unit disk in [9],on the Bergman space of the polydisk in [10]and on the Bergman space of the unit ball in [7,11].Unfortunately,Sarason’s conjecture was eventually proved to be false,both on the Hardy space and the Bergman space,see [1,6]for counterexamples.However,in [2–3],the Sarason’s conjecture was proved to be true on the Fock space,and in this setting,the explicit forms of the symbolsfandgwere given.Although the boundedness of a single Toeplitz operator on Fock space is still an open problem,some progress has been made in Toeplitz products and Hankel products.Ma,Yan,Zheng and Zhu [5]gave a sufficient but not necessary condition on bounded Hankel productforf,gin the Fock space.Yan and Zheng [12]characterized bounded Toeplitz productTfTgand Hankel productH∗fHgon Fock space for two polynomialsfandginz,∈C.Inspired by these work,we study the boundedness of Toeplitz productTfTgand Hankel productH∗fHgonF2,mfor two polynomialsf,g∈P,where

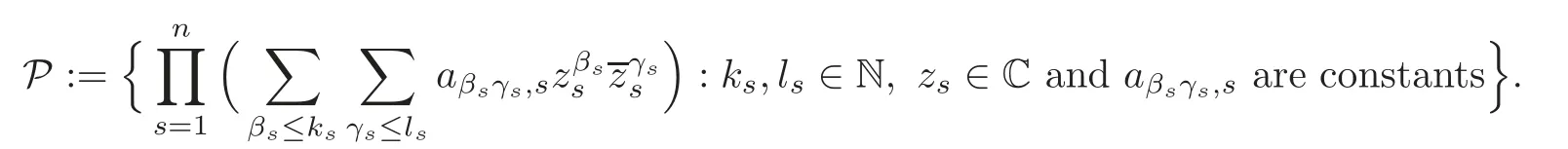
Our main results can be stated as follows.

Theorem 1.1Let f,g∈P.Then the Toeplitz product TfTgis bounded on F2,mif and only if both f and g are constants.

Theorem 1.2Let f,g∈P.Then the Hankel product H∗fHgis bounded on F2,mif and only if at least one of the following statements holds:

(1)f is holomorphic.

(2)g is holomorphic.

(3)n=1and there exist two holomorphic polynomials f1and g1such that

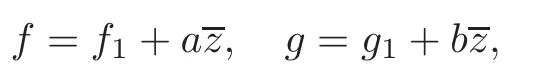
where a,b are constants and z,∈C.

We would like to mention that all the conclusions for the Fock-Sobolev spaceF2,min this paper are consistent with the results in [12]whenm=0 andn=1,but the boundedness characterization of Hankel product forn≥2 is essentially different fromn=1 and all the results form≥1 are new.

The layout of the paper is as follows.In Section 2 we give the proof of characterizations of bounded Toeplitz productTfTgonF2,m.In Section 3 we give the proof of characterizations of bounded Hankel productH∗fHg.

In what follows,denote byχEthe characteristic function of a measurable setE.We say a multi-indexα=(α1,···,αn) ∈Nntends to ∞if each componentαitends to ∞.For two arbitrary sequencesAαandBαdepending on multi-indexα=(α1,···,αn),we use the notationAα∼Bαto denote the relationship:

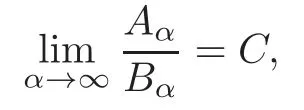
whereCis a positive constant independent ofα.

Recall that the Stirling’s formula is stated as

wherekis a positive integer and “∼” can be understood in the sense that the ratio of the two sides tends to 1 askgoes to ∞.

2 Toeplitz Products

In this section,we are going to characterize bounded Toeplitz productTfTgwithf,g∈P.Forα∈Nnandz∈Cn,the functions

form an orthonormal basis forF2,m,see [4]for more details.

Givenα=(α1,···,αn),β=(β1,···,βn)∈Nn,the addition and the subtraction ofαandβare defined by

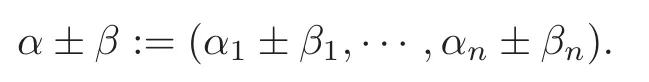
We callα≥β(resp.α>β,α≤β,α<β) ifαi≥βi(resp.αi>βi,αi≤βi,αi<βi) for eachi=1,···,n.

We now give a technical result that will be frequently used in the following.

Lemma 2.1Let{eα:α∈Nn}be any orthonormal basis of F2,m.Then for any β,γ∈Nnand z∈Cn,we have

ProofDirect verifications give

and

Forη≠α+β−γ,it is easy to see that

Forη=α+β−γ,applying integration in polar coordinates and using [14,Lemma 1.11],we obtain

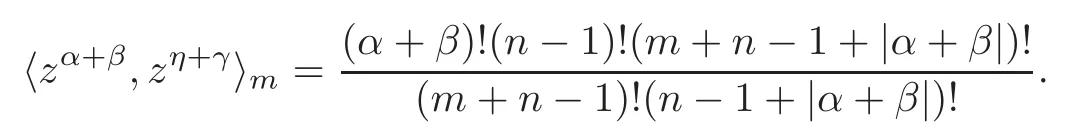
Notice that ifα+β−γ≥0,then there exists a uniqueηin (2.2)such thatη=α+β−γ.Thus

This together with (2.1) gives

Ifα+β−γis less than 0,thenη≠α+β−γfor allηin (2.2),it follows from(2.1)–(2.3)thatTzβzγeα=0. This completes the proof.

In order to state the following lemma effectively,for any functionf,we define

Lemma 2.2Suppose β=(β1,···,βn),γ=(γ1,···,γn),k=(k1,···,kn)and l=(l1,···,ln)are inNn.For any z=(z1,···,zn)∈Cn,let

where aµi,bνiare constants with aki,blinonzero for each i=1,···,n.For i1,···,in,j1,···,jn∈{0,1},let

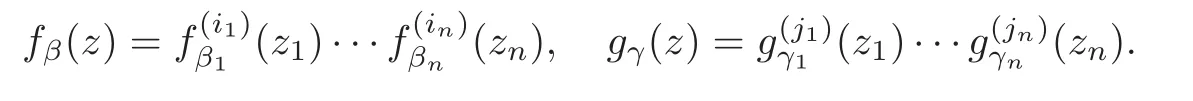
Then each of the Toeplitz products TfβTgγis bounded on F2,mif and only if β=γ=k=l=(0,···,0).

ProofFor simplicity,we seti=(i1,···,in),j=(j1,···,jn) and denote

Forα∈Nnsatisfyingαs≥χ{1}(js)γs+χ{1}(is)βs(s=1,···,n),we apply Lemma 2.1 twice to obtain

where

An application of Stirling’s formula implies that

Sinceaki,bliare nonzero constants for eachi=1,···,n,it follows from (2.5) and (2.6) that

Therefore,if we denote

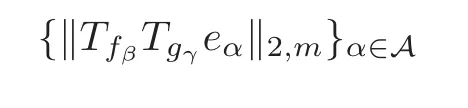
then the Toeplitz productTfβTgγis bounded if and only if is uniformly bounded onF2,m,which is equivalent toβ=γ=k=l=(0,···,0).This completes the proof of Lemma 2.2.

Next,we will use Lemma 2.2 to prove the main theorem in this section.To this end,we first recall that,iff∈P,then there existk=(k1,···,kn) andl=(l1,···,ln)∈Nnsuch that

For anys=1,···,n,let

and

For each integerθssatisfyingi0,s≤θs≤i1,s(s=1,···,n),letFθs(zs) be the sum of all those termsaβsγszβsin the polynomial formula (2.7) offsuch thatβs−γs=θs.If there is no such kind of term,we setFθs=0.ThenFθsis of the same form as the functionfβs(ifθs≥0) or the complex conjugate offβs(ifθs<0) in Lemma 2.2.Thus,with this new notation,the expression in (2.7) may be rewritten as

Now,we give the proof of the first main result.

Proof of Theorem 1.1If bothfandgare constants,then it is easy to check that Toeplitz operatorsTfandTgare both bounded onF2,m.Hence the Toeplitz productTfTgis bounded onF2,m.

Conversely,suppose that the Toeplitz productTfTgis bounded.Sincef,g∈P,from the above discussion,fandgadmit expansions:

for simplicity.Therefore

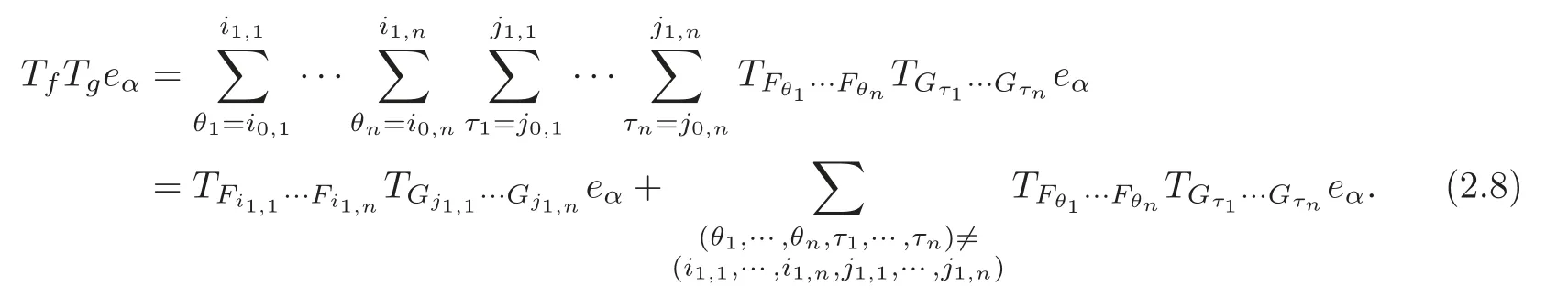
Set multi-index

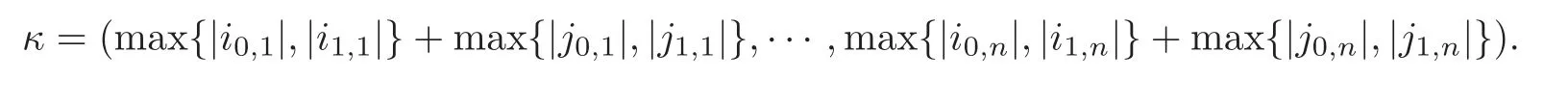
It follows from the definitions ofFθs,Gτtand the proof of Lemma 2.2 that for anyα≥κ,β=(θ1,···,θn),γ=(τ1,···,τn) withi0,s≤θs≤i1,sandj0,t≤τt≤j1,t(s,t=1,···,n)such that (θ1,···,θn,τ1,···,τn)≠(i1,1,···,i1,n,j1,1,···,j1,n),we have

Notice that the first term of (2.8),

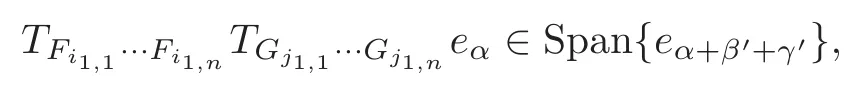
whereβ′=(i1,1,···,i1,n) andγ′=(j1,1,···,j1,n),we see thatTFi1,1···Fi1,nTGj1,1···Gj1,neαis orthogonal to the second term of (2.8) forα≥κ.It follows that

Obviously,the boundedness ofTfTgimplies the boundedness ofTFi1,1···Fi1,nTGj1,1···Gj1,n.This along with Lemma 2.2 implies thatFi1,1,···,Fi1,nandGj1,1,···,Gj1,nmust be constants.Similarly,we can also conclude thatTFi0,1···Fi0,nTGj0,1···Gj0,nis bounded if (2.8) is replaced by

where the summation is taken over alli0,1≤θ1≤i1,1,···,i0,n≤θn≤i1,n,j0,1≤τ1≤j1,1,···,j0,n≤τn≤j1,nsuch that (θ1,···,θn,τ1,···,τn)≠(i0,1,···,i0,n,j0,1,···,j0,n).By Lemma 2.2 again,Fi0,1,···,Fi0,nandGj0,1,···,Gj0,nmust be constants.Thusfandgare constants.This completes the proof of Theorem 1.1.

Corollary 2.1Assume that f∈P.Then the Toeplitz operator Tfis bounded on F2,mif and only if f is a constant.

ProofIt follows from Theorem 1.1 by settingg=1 org=f.

3 Hankel Products

In this section,we are to characterize bounded Hankel productsH∗fHgwithf,g∈P.For technical reasons,we require the following lemma.

Lemma 3.1Assume β=(β1,···,βn),γ=(γ1,···,γn),µ=(µ1,···,µn)and ν=(ν1,···,νn)are all inNn.Let f=and g=zµfor z,∈Cn.Then for any α≥(|γ1−β1|+|µ1−ν1|,···,|γn−βn|+|µn−νn|),we have

where

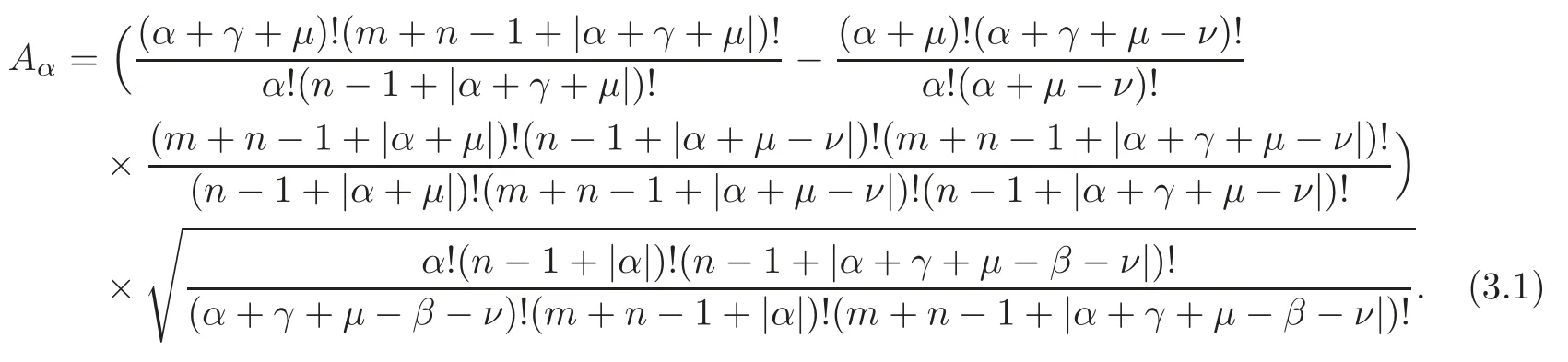
Furthermore,Aα=0if and only if γ=0or ν=0.And if Aα≠0,then

ProofWe only give the proof for the case ofm≠0,since the case ofm=0 is much simpler.It is easy to verify that

It follows from Lemma 2.1 that for anyα≥(|γ1−β1|+|µ1−ν1|,···,|γn−βn|+|µn−νn|),we have

Applying Lemma 2.1 again,we obtain

Combining (3.3)–(3.5),we deduce the explicit formula forAαin (3.1).From this formula,it is not hard to see thatAα=0 is equivalent toγ=0 orν=0.

IfAα≠0,then by Stirling’s formula,we have

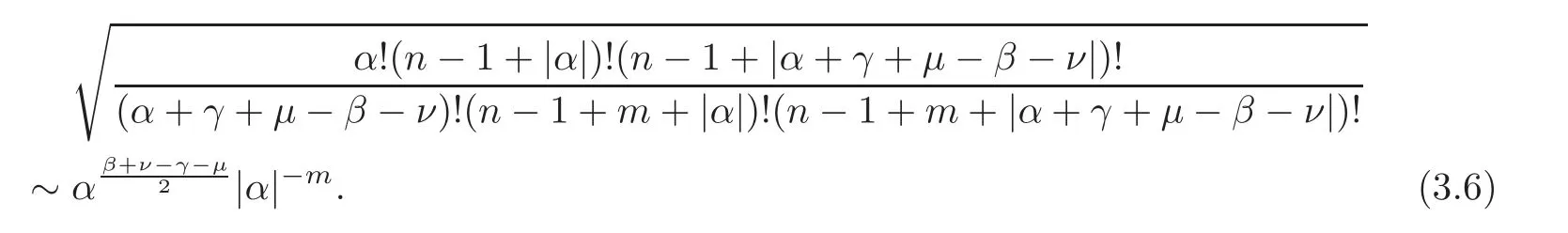
Denote

for simplicity.Next,we study the asymptotic behavior ofBαas each componentαjtends to infinity.Firstly,we estimate the first term ofBα.

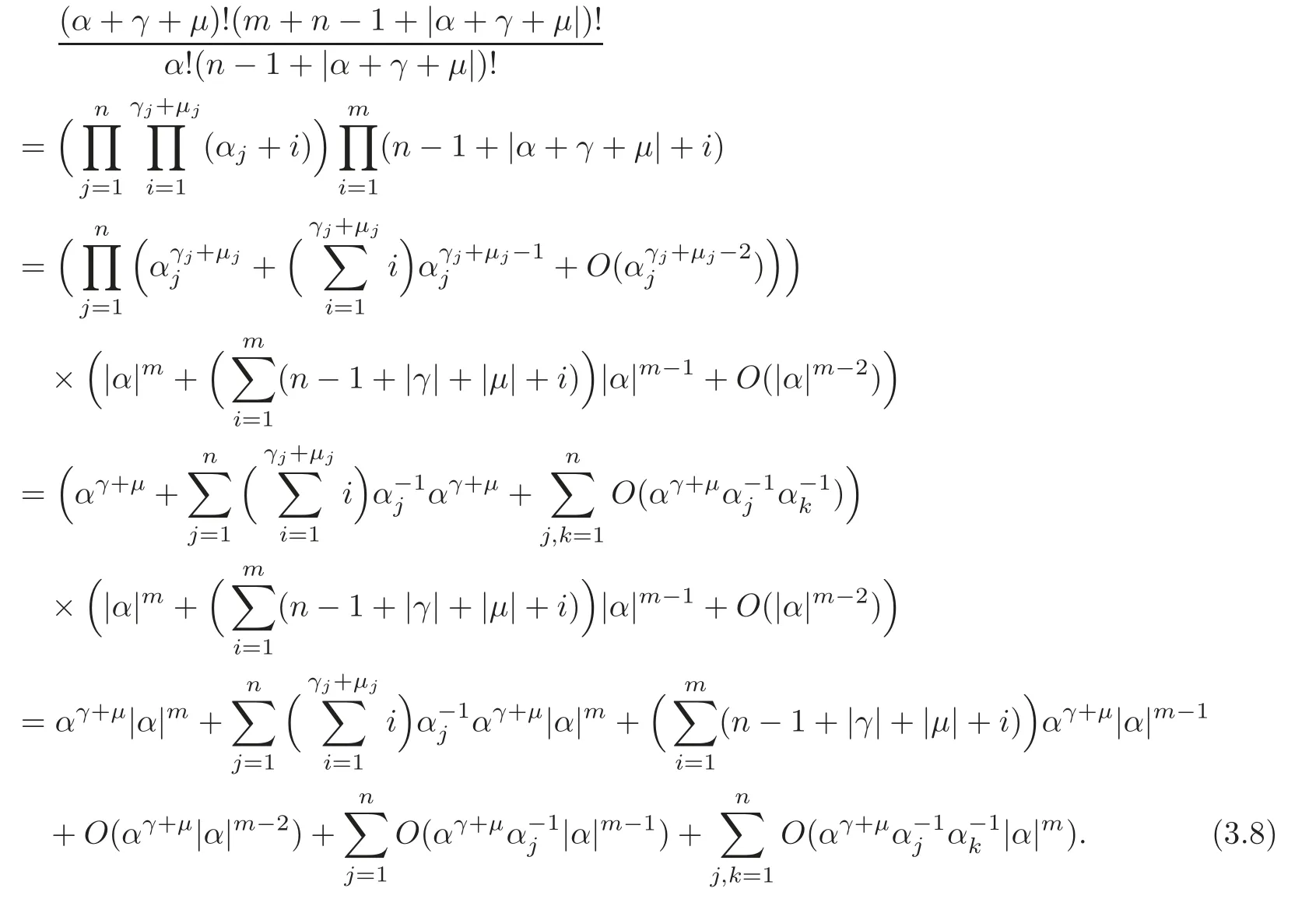
Besides,

and

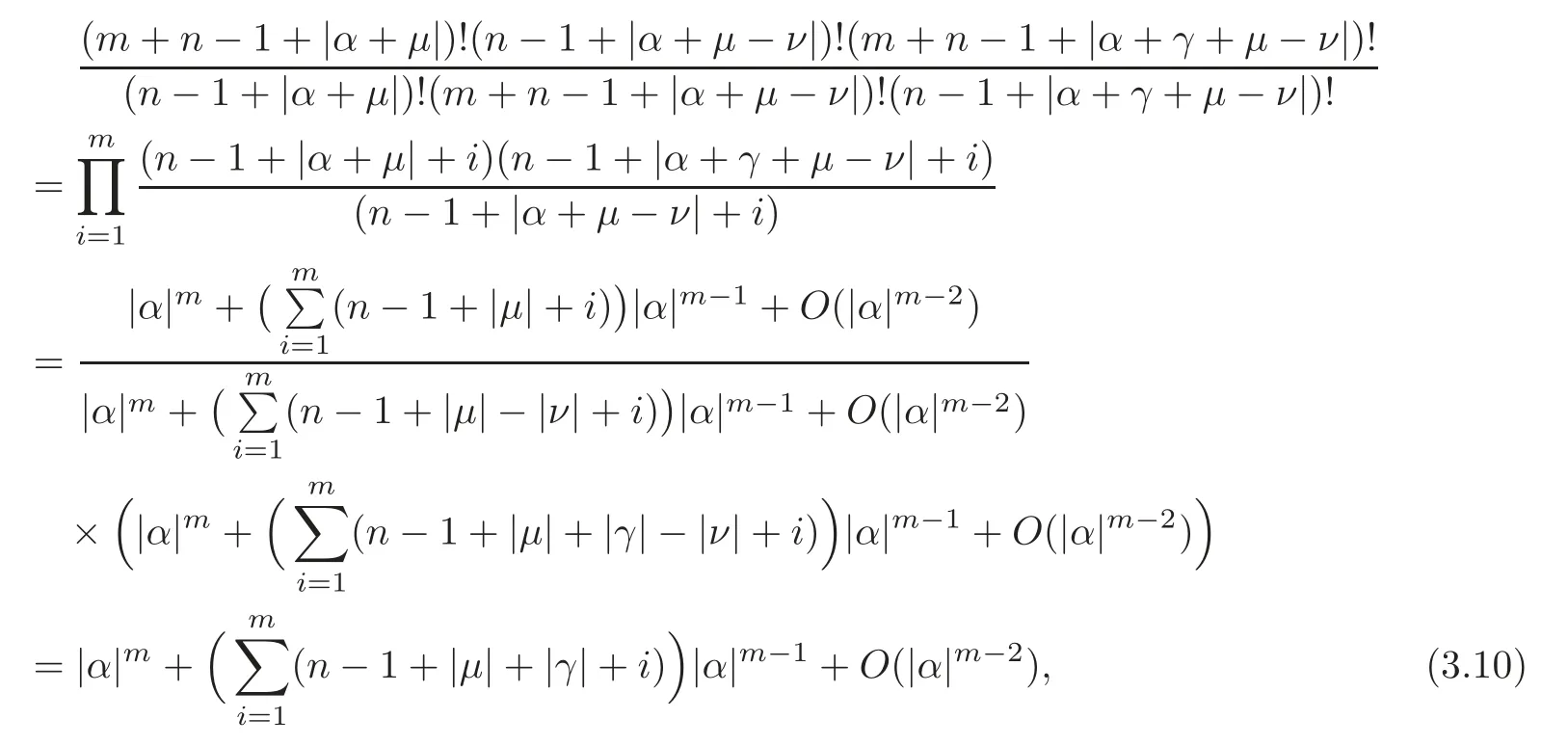
which implies that

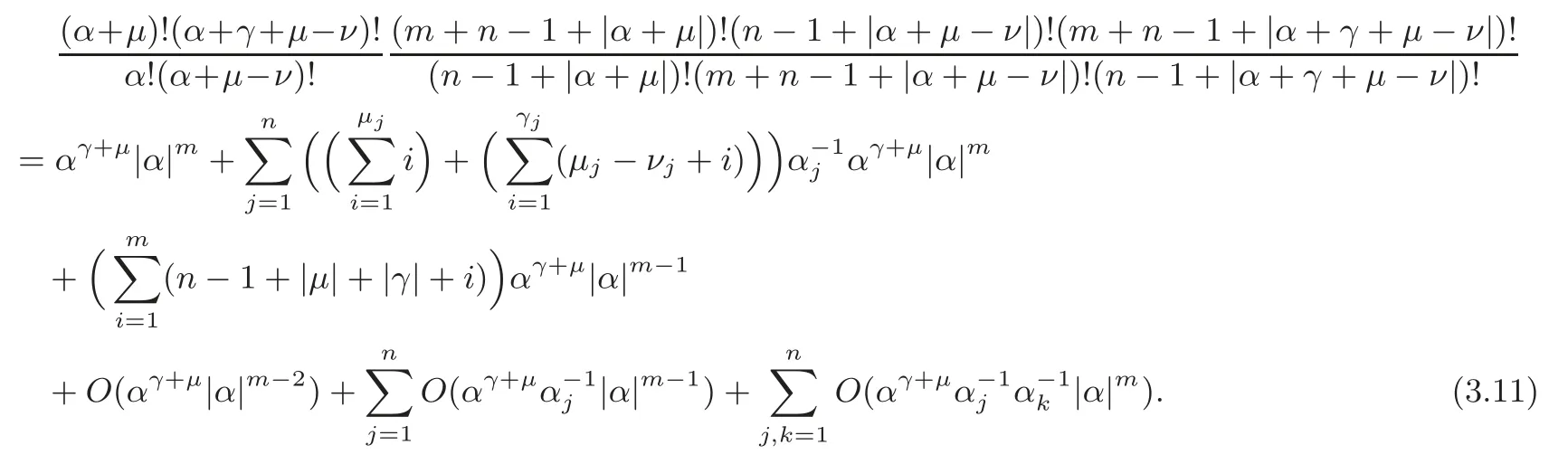
(3.11) Subtracted from (3.8),we obtain

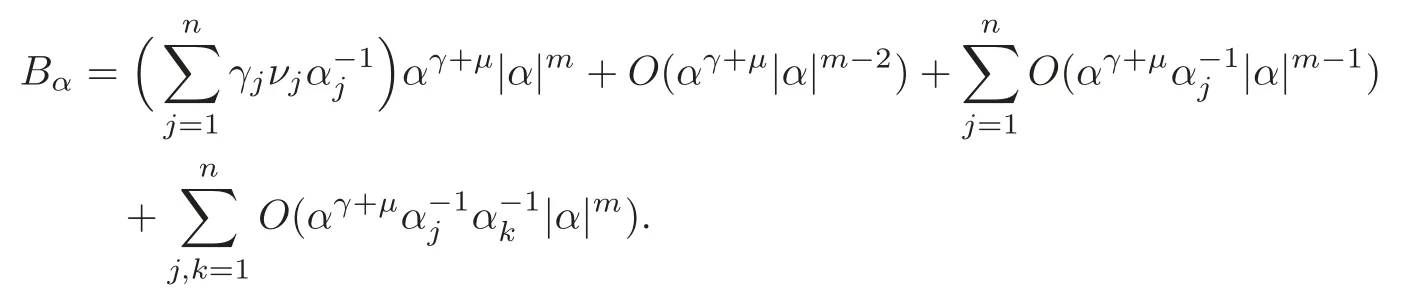
This along with (3.6) gives

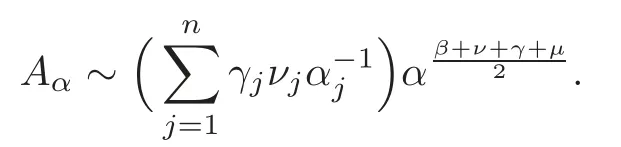
This completes the proof of Lemma 3.1.

Lemma 3.2Suppose β=(β1,···,βn),γ=(γ1,···,γn),k=(k1,···,kn)and l=(l1,···,ln)are inNn.For any z=(z1,···,zn)∈Cn,let

where aµi,bνiare constants with aki,blinonzero for each i=1,···,n.For i1,···,in,j1,···,jn∈{0,1},let

Then the Hankel product H∗fβHgγis bounded on F2,mif and only if at least one of the following conditions holds:

(1)k=(0,···,0)and βs=0for any1≤s≤n such that is=1.

(2)l=(0,···,0)and γt=0for any1≤t≤n such that jt=1.

(3)n=β1=γ1=i1=j1=1and k1=l1=0.

ProofTo begin with,we use the same notationsθ,ϑ,ϕandψas in Lemma 2.2.Then by Lemma 3.1,for anyα∈Nnsatisfyingα≥β+γ,

where

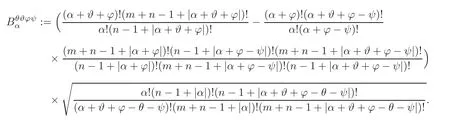
Ifϑ≠0 andψ≠0,then by Lemma 3.1 again,we have≠0 and

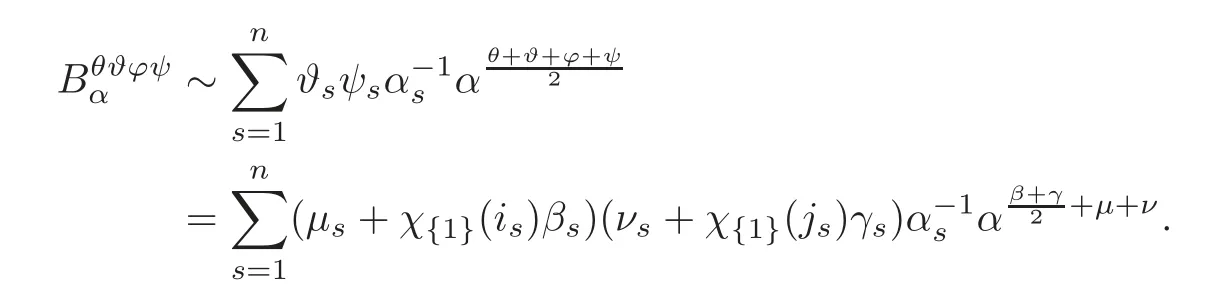
Sinceaki,bliare nonzero constants for eachi=1,···,n,we have

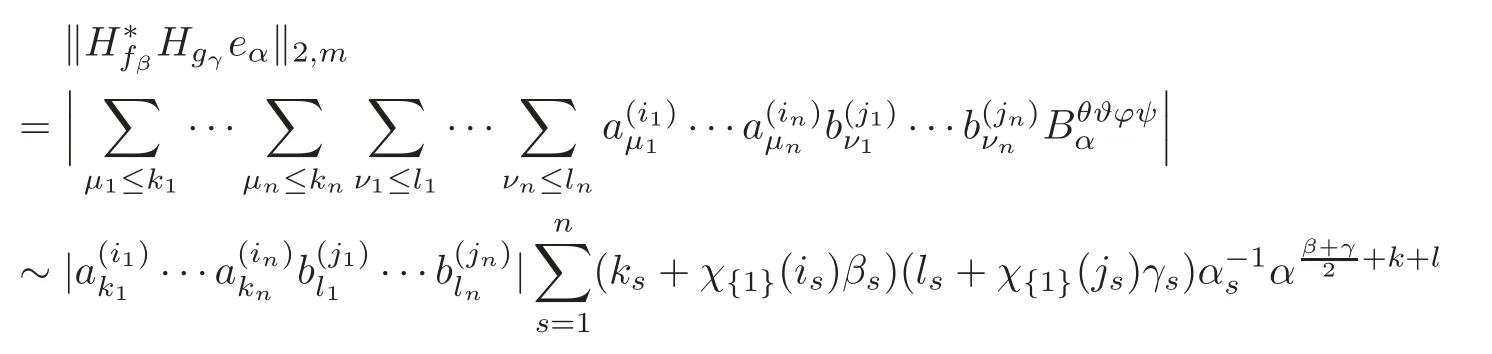
forα≥β+γ.Consequently,the Hankel productH∗fβHgγis bounded onF2,mif and only if the following expression

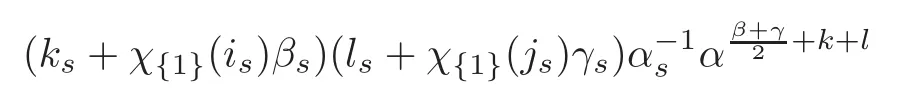
is independent ofαfor eachs=1,···,n,which is equivalent to that at least one of the following statements holds:

(a) (ks+χ{1}(is)βs)(ls+χ{1}(js)γs)=0 for eachs=1,···,n.

(b)n=β1=γ1=i1=j1=1 andk1=l1=0.

Since (a) is equivalent to condition (1) or (2),the desired result is then obtained.

We proceed to prove the main theorem in this section.

Proof of Theorem 1.2If the statement (1) or (2) is true,thenH∗f=0 orHg=0,it follows thatH∗fHgis bounded onF2,m.If the statement (3) is true,then we have

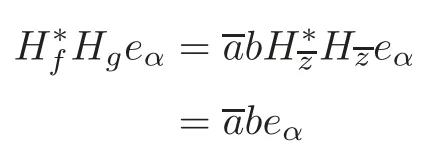
by Lemma 3.2,which implies that the Hankel productH∗fHgis bounded onF2,m.

Conversely,assume the Hankel productH∗fHgis bounded onF2,m.If neitherfnorgis holomorphic,we are to show that the statement (3) must be true.Sincef∈P,there existk=(k1,···,kn) andl=(l1,···,ln)∈Nnsuch that

Let

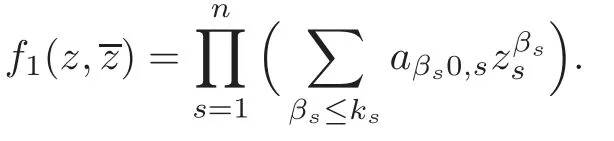
Thenf1is said to be the pure holomorphic part off.Similarly,denoteg1by the pure holomorphic part ofg.Letf2=f−f1andg2=g−g1.Then by our assumption,we see that neitherf2norg2is 0.Moreover,from the discussion before Theorem 1.1,f2andg2admit expansions

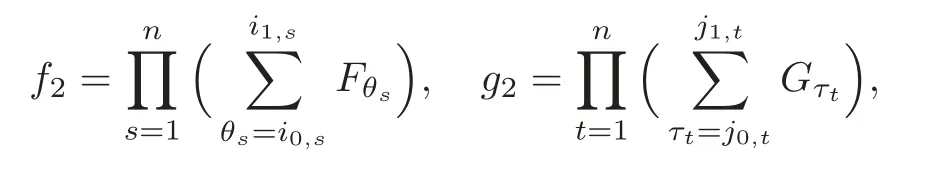
whereFi0,s,Fi1,s,Gj0,sandGj1,sare nonzero.Therefore,

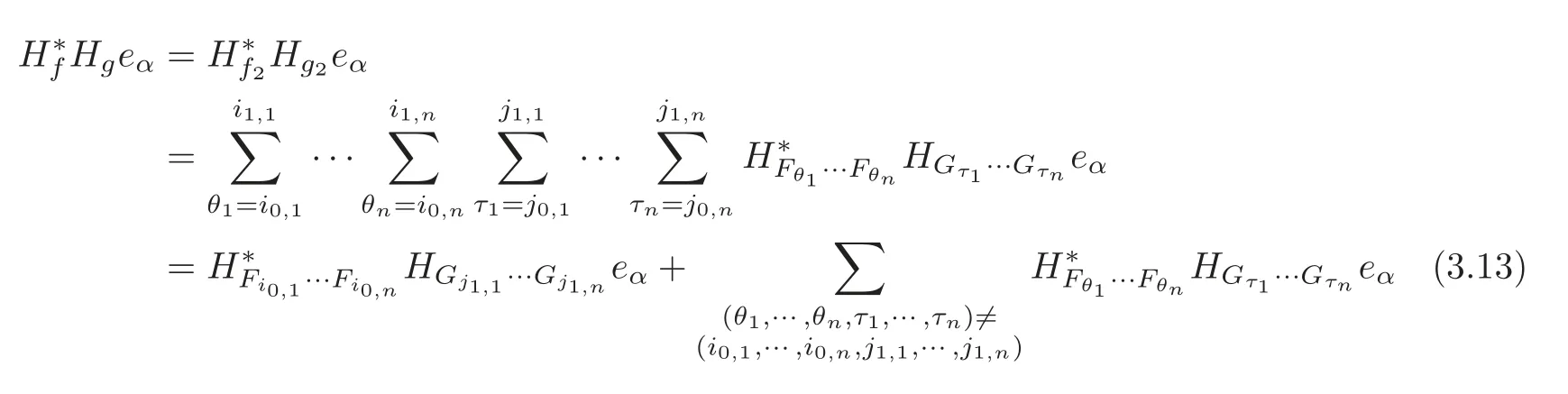
for anyα∈Nn.Set multi-index

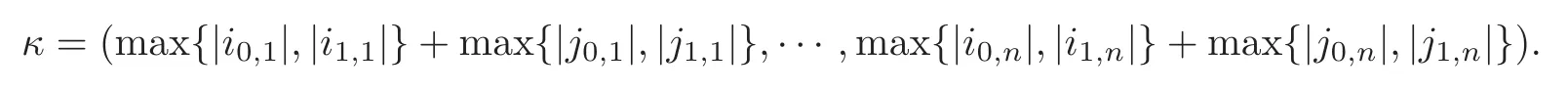
It follows from the definitions ofFθs,Gτtand the proof of Lemma 3.2 that for anyα≥κ,β=(θ1,···,θn),γ=(τ1,···,τn) withi0,s≤θs≤i1,sandj0,t≤τt≤j1,t(s,t=1,···,n)satisfying (θ1,···,θn,τ1,···,τn)≠(i1,1,···,i1,n,j1,1,···,j1,n),we have

But the first term of (3.13),

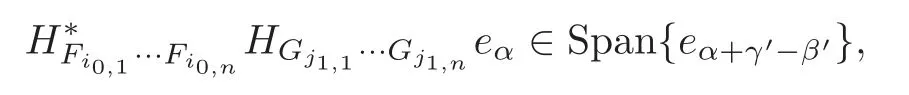
whereγ′=(i0,1,···,i0,n) andβ′=(j1,1,···,j1,n).Therefore,we conclude that

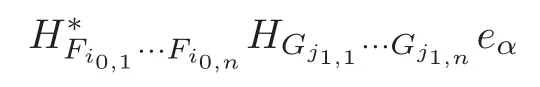
is orthogonal to the second term of (3.13) forα≥κ.This makes

forα≥κ.Carefully examining the proof of Lemma 3.2,we see thatH∗Fi1,1···Fi1,nHGj1,1···Gj1,neαis bounded onF2,mif and only if the sequence

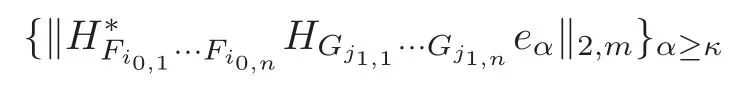
is bounded onF2,m.

Notice from the definitions off2andg2that,forθs≥0 (resp.τt≥0),Fθs(resp.Gτt) does not contain any term as(resp.bτtztτt),whereaθs(resp.bτt) denotes the coefficient.In other words,forθs≥0 (resp.τt≥0),the termFθs(resp.Gτt) is of the following form:

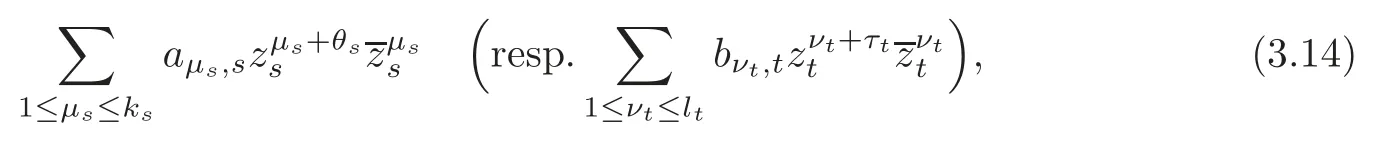
whereksandltare positive integers greater than or equal to 1.

Forθs<0 (resp.τt<0),the termFθs(resp.Gτt) is of the following form:

Ifi0,s≥0 orj1,t≥0 for alls,t=1,···,n,then it follows from (3.14) and Lemma 3.2 thatH∗Fi0,1···Fi0,nHGj1,1···Gj1,nis unbounded.Thus,the boundedness ofH∗Fi0,1···Fi0,nHGj1,1···Gj1,nimplies thati0,s<0 andj1,t<0 for alls,t=1,···,n.ThenFθsis the form of (3.15).It follows from (3) of Lemma 3.2,we haven=1 andFi0,1=a0,Gj1,1=b0,wherea0,b0are nonzero constants andz∈C.

As discussed above,we can also conclude that the Hankel product is bounded if (3.13) is replaced by

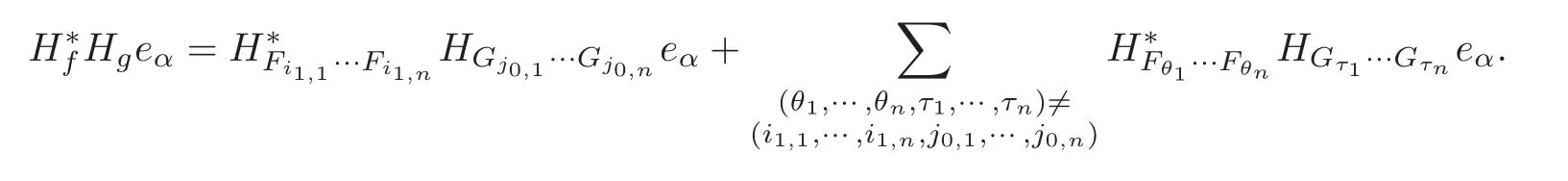
Similar to the discussion ofH∗Fi0,1···Fi0,nHGj1,1···Gj1,neα,we can also conclude thatn=1 andFi1,1=a′0,Gj0,1=b′0,wherea′0,b′0are nonzero constants and∈C.Therefore,f2(z)=andg2(z)=,whereaandbare nonzero constants and∈C,hence the statement (3) is true.This completes the proof of Theorem 1.2.

Corollary 3.1Assume that f∈P.Then the Hankel operator Hfis bounded on F2,mif and only if one of the following statements is true:

(1)f is holomorphic.

(2)n=1and there exists a holomorphic polynomial f1such that

where a is a constant and z∈C.

ProofIt is a direct consequence of Theorem 1.2 by settingg=f.

Corollary 3.2Assume that f∈P.Then the Hankel operator Hfis compact on F2,mif and only if f is holomorphic.

AcknowledgementThe authors would like to thank the referee for his/her valuable comments.