Canonical Connections and Algebraic Ricci Solitons of Three-dimensional Lorentzian Lie Groups∗

Yong WANG

1School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China.E-mail: wangy581@nenu.edu.cn

Abstract In this paper,the author computes canonical connections and Kobayashi-Nomizu connections and their curvature on three-dimensional Lorentzian Lie groups with some product structure.He defines algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections.He classifies algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections on three-dimensional Lorentzian Lie groups with some product structure.

Keywords Canonical connections,Kobayashi-Nomizu connections,Algebraic Ricci solitons,Three-dimensional Lorentzian Lie groups

1 Introduction

The concept of the algebraic Ricci soliton was first introduced by Lauret in Riemannian case in[6],where the author studied the relation between solvsolitons and Ricci solitons on Riemannian manifolds.More precisely,he proved that any Riemannian solvsoliton metric is a Ricci soliton.The concept of the algebraic Ricci soliton was extended to the pseudo-Riemannian case in [1],where Batat and Onda studied algebraic Ricci solitons of three-dimensional Lorentzian Lie groups.They got a complete classification of algebraic Ricci solitons of three-dimensional Lorentzian Lie groups and they proved that,contrary to the Riemannian case,Lorentzian Ricci solitons needed not be algebraic Ricci solitons.In [7],Onda provided a study of algebraic Ricci solitons in the pseudo-Riemannian case and obtained a steady algebraic Ricci soliton and a shrinking algebraic Ricci soliton in the Lorentzian setting.In [5],Etayo and Santamaria studied some affine connections on manifolds with the product structure or the complex structure.In particular,the canonical connection and the Kobayashi-Nomizu connection for a product structure were studied.In this paper,we introduce a particular product structure on three-dimensional Lorentzian Lie groups and we compute canonical connections and Kobayashi-Nomizu connections and their curvatures on three-dimensional Lorentzian Lie groups with this product structure.We define algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections.We classify algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections on three-dimensional Lorentzian Lie groups with this product structure.

In Section 2,we classify algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections on three-dimensional unimodular Lorentzian Lie groups with the product structure.In Section 3,we classify algebraic Ricci solitons associated to canonical connections and Kobayashi-Nomizu connections on three-dimensional non-unimodular Lorentzian Lie groups with the product structure.

2 Algebraic Ricci Solitons Associated to Canonical Connections and Kobayashi-Nomizu Connections on Three-dimensional Lorentzian Lie Groups

Three-dimensional Lorentzian Lie groups have been classified in[2,4](see[1,Theorems 2.1–2.2]).Throughout this paper,we shall by{Gi}i=1,···,7,denote the connected,simply connected three-dimensional Lie group equipped with a left-invariant Lorentzian metricgand having Lie algebra {g}i=1,···,7.Let ∇be the Levi-Civita connection ofGiandRbe its curvature tensor,taken with the convention

The Ricci tensor of (Gi,g) is defined by

where {e1,e2,e3} is a pseudo-orthonormal basis,withe3timelike and the Ricci operator Ric is given by We define a product structureJonGiby

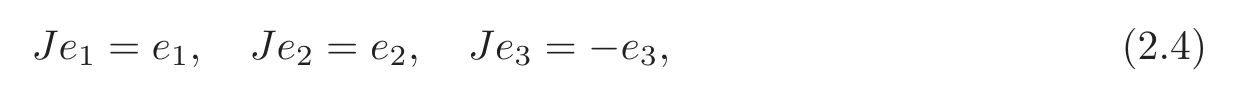
thenJ2=Id andg(Jej,Jej)=g(ej,ej).By [5],we define the canonical connection and the Kobayashi-Nomizu connection as follows:

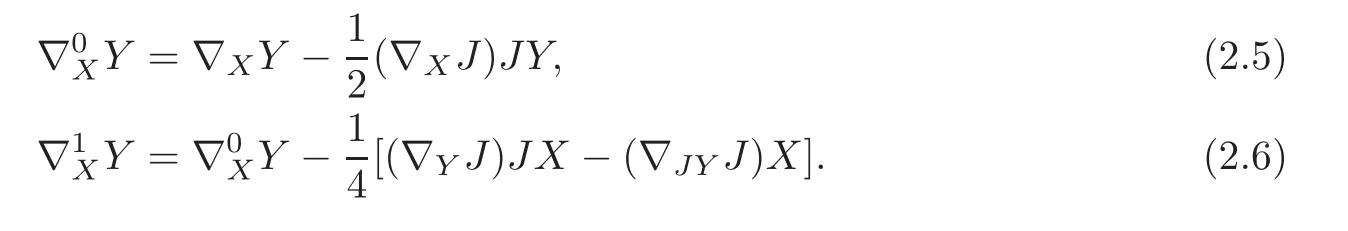
We define

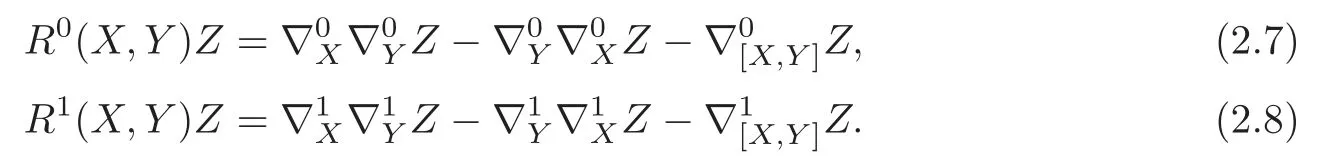
The Ricci tensors of (Gi,g) associated to the canonical connection and the Kobayashi-Nomizu connection are defined by

The Ricci operators Ric0and Ric1is given by

Let

and

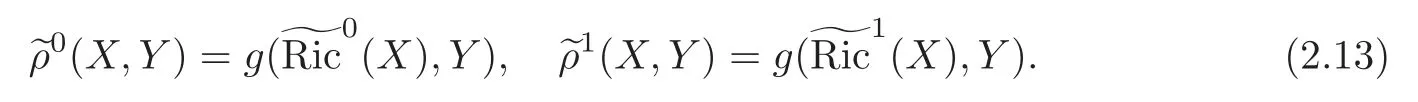
Definition 2.1(Gi,g,J)is called the first(resp.second)kind algebraic Ricci soliton associated to the connection∇0if it satisfies

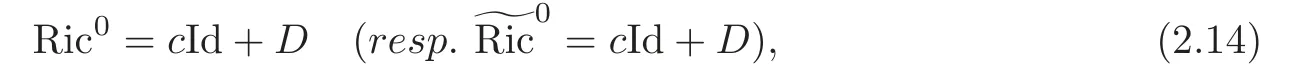
where c is a real number,and D is a derivation ofg,that is

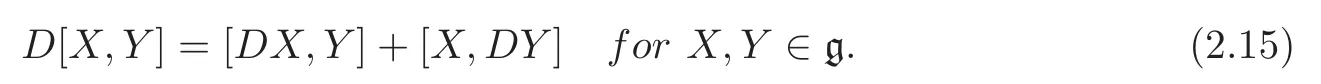
(Gi,g,J)is called the first(resp.second)kind algebraic Ricci soliton associated to the connection∇1if it satisfies

By[1,Lemma 3.1],we have that forG1,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG1satisfies

We recall (see [1,3]) that the Levi-Civita connection ∇ofG1is given by

By (2.4) and (2.18),we have that forG1,the following equalities hold

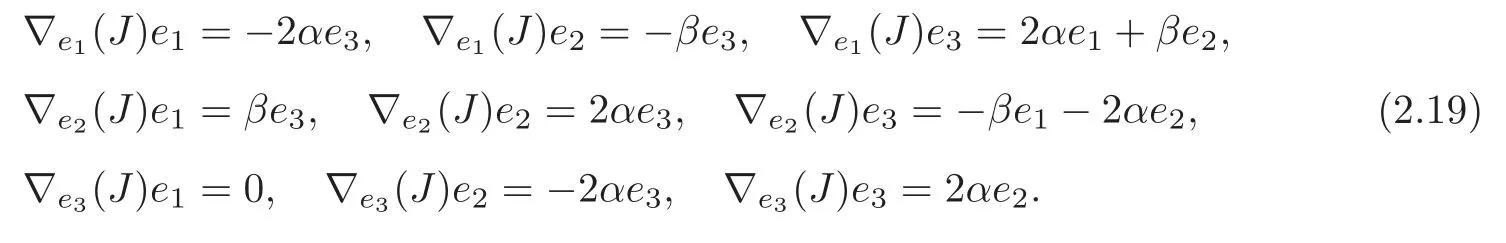
By (2.4)–(2.5) and (2.18)–(2.19),we have the following.

The canonical connection ∇0of (G1,J) is given by

By(2.7)and(2.20),we have that the curvatureR0of the canonical connection ∇0of(G1,J)is given by

By (2.9),(2.11) and (2.21),we get

If (G1,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

By (2.15) and (2.23),we getα2+c=0,β=0.Then we have the following theorem.

Theorem 2.1(G1,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if α2+c=0,β=0,α≠0.In particular,

By (2.12)–(2.13) and (2.22),we have

If (G1,g,J) is the second kind algebraic Ricci soliton associated to the connection ∇0,then=cId+D,so

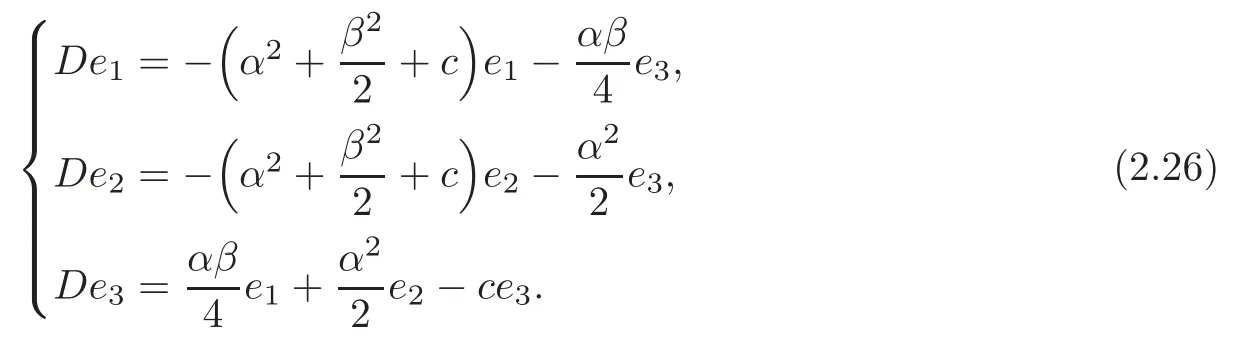
Theorem 2.2(G1,g,J)is the second kind algebraic Ricci soliton associated to the connec-tion∇0if and only ifIn particular,

By (2.6) and (2.19)–(2.20),we have that the Kobayashi-Nomizu connection ∇1of (G1,J)is given by

By (2.8) and (2.28),we have that the curvatureR1of the Kobayashi-Nomizu connection∇1of (G1,J) is given by

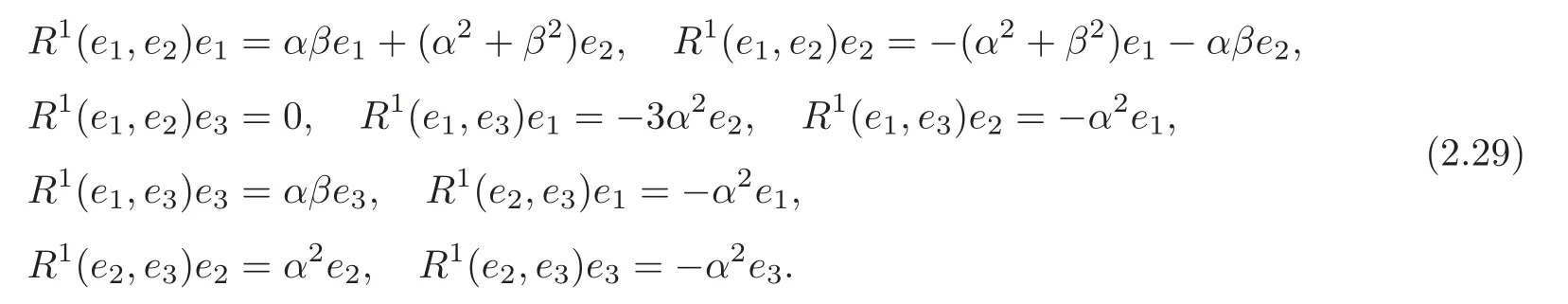
By (2.10)–(2.11)and (2.29),we get

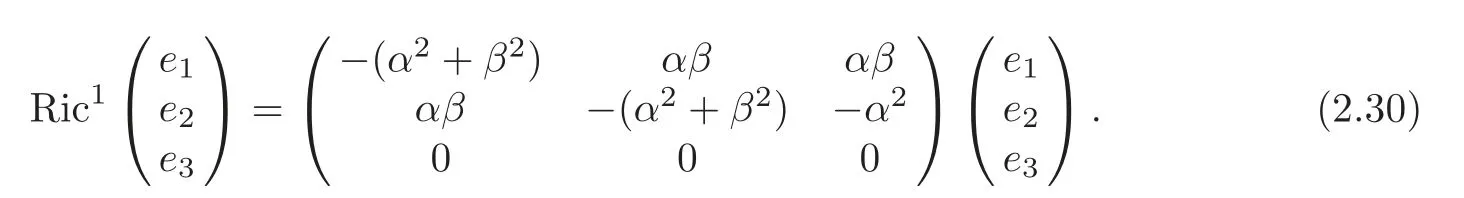
If (G1,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇1,then Ric1=cId+D,so

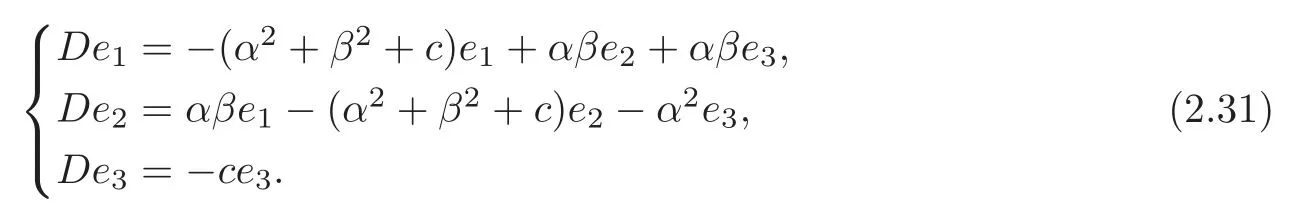
By (2.15) and (2.31),we getβ=0,c=0.Then we have the following theorem.

Theorem 2.3(G1,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if β=0,c=0,α≠0.In particular,

By (2.12)–(2.13) and (2.30),we have

If (G1,g,J) is the second kind algebraic Ricci soliton associated to the connection ∇1,then=cId+D,so

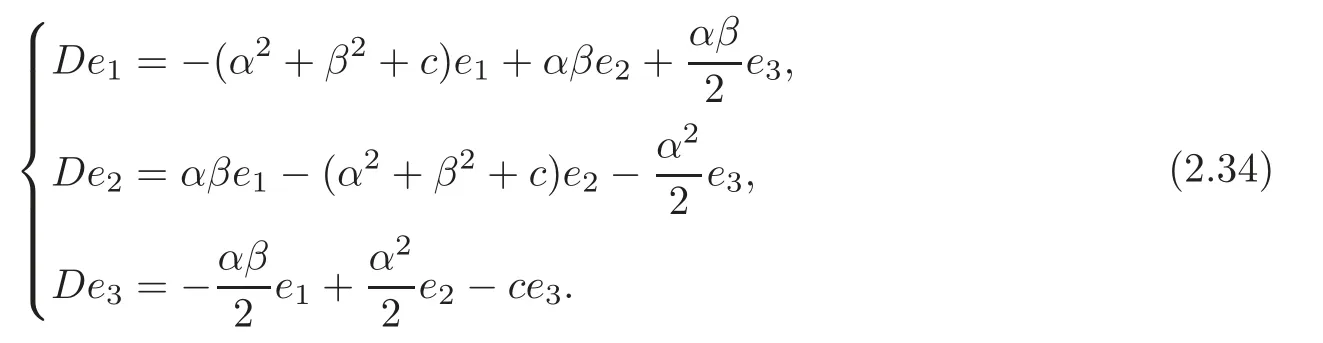
Theorem 2.4(G1,g,J)is the second kind algebraic Ricci soliton associated to the connec-tion∇1if and only ifIn particular,

By[1,Lemma 3.5],we have that forG2,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG2satisfies

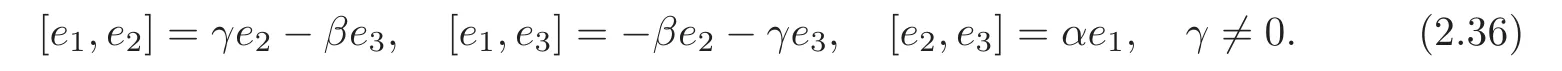
Similar to the case ofG1,we have the following theorem.

Theorem 2.5(1) (G2,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if α=β=0,γ2+c=0,γ≠0.In particular,

(2) (G2,g,J)is the second kind algebraic Ricci soliton associated to the connection∇0if and only if α=β=0,γ2+c=0,γ≠0.In particular,

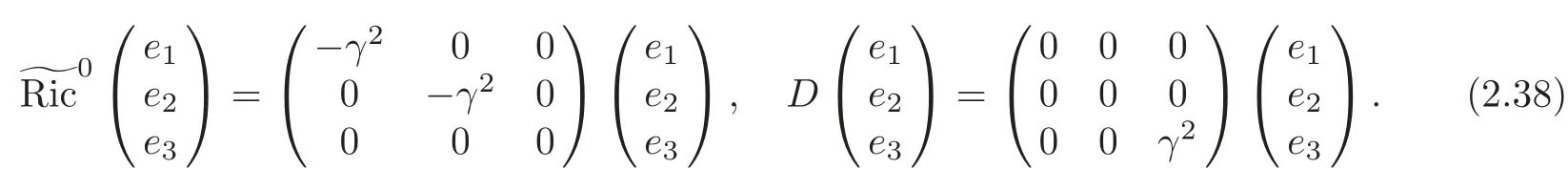
(3) (G2,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if α=β=0,γ2+c=0,γ≠0.In particular,

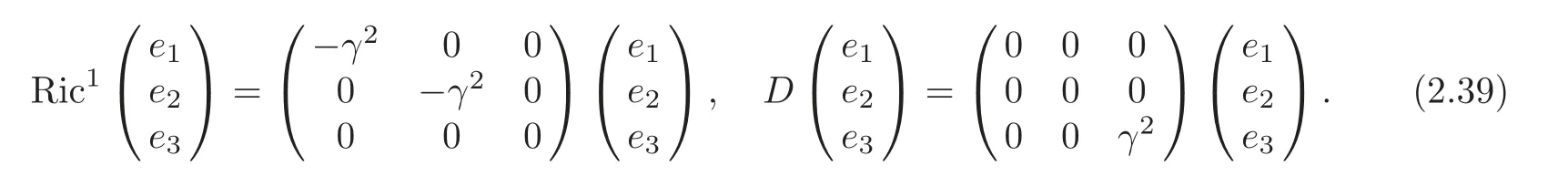
(4) (G2,g,J)is the second kind algebraic Ricci soliton associated to the connection∇1if and only if α=β=0,γ2+c=0,γ≠0.In particular,

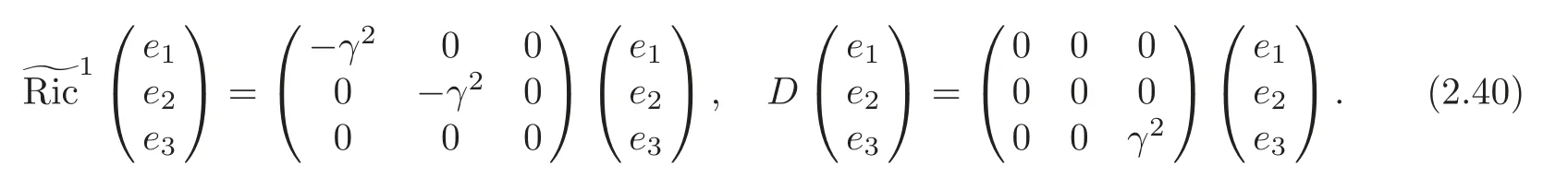
ProofThe canonical connection ∇0of (G2,J) is given by

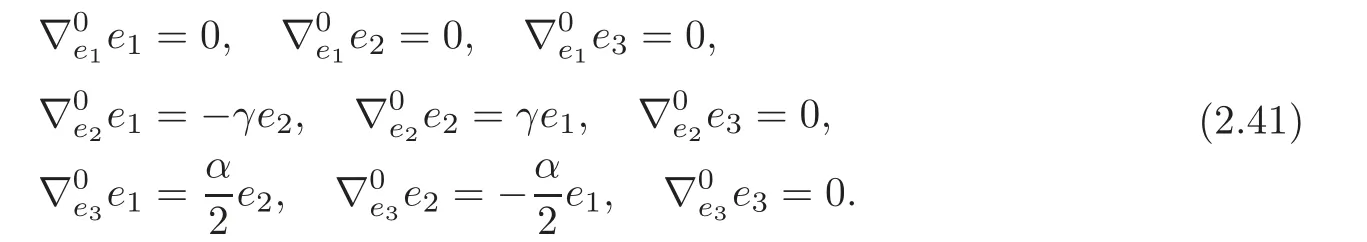
By (2.7) and (2.41),we have that the curvatureR0of the canonical connection ∇0of (G2,J)is given by

By (2.9),(2.11) and (2.42),we get for (G2,∇0),

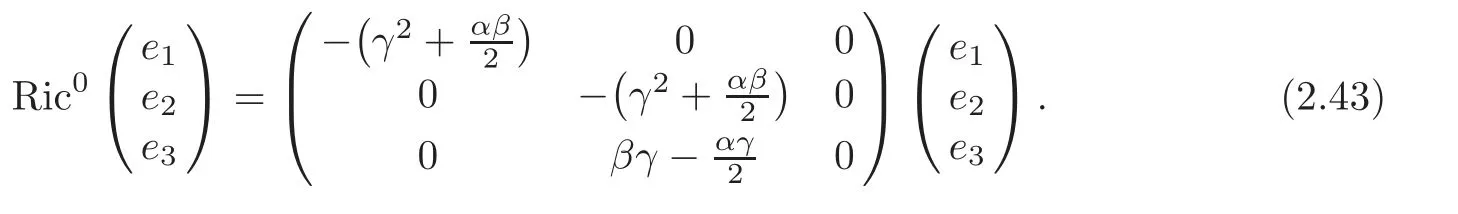
If (G2,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

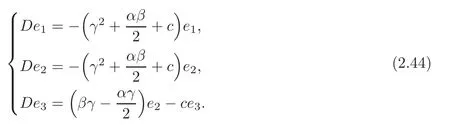
By (2.15)and (2.44),we getα=β=0,γ2+c=0.Then case (1)holds.The other three cases hold similarly.

By[1,Lemma 3.8],we have that forG3,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG3satisfies

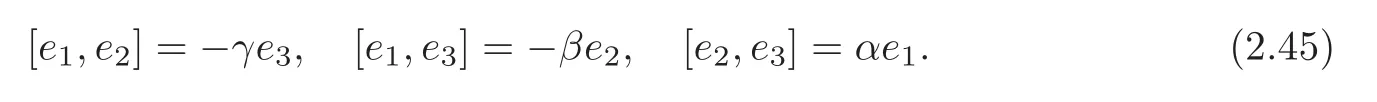
Theorem 2.6(1) (G3,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)α=β=γ=0.In particular,

(ii)α=β=0,γ2=c.In particular,

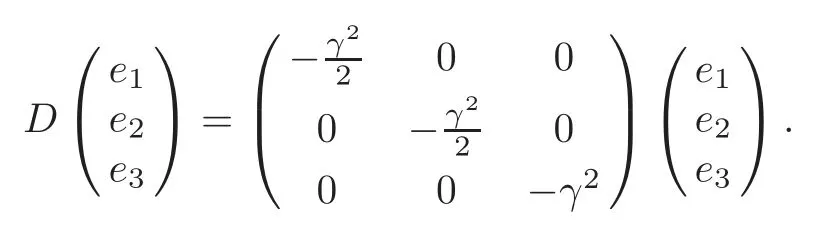
(iii)α≠0or β≠0,γ=0,c=0.In particular,

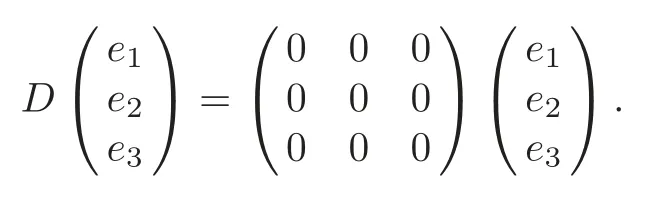
(iv)α≠0or β≠0,γ=α+β,c=0.In particular,

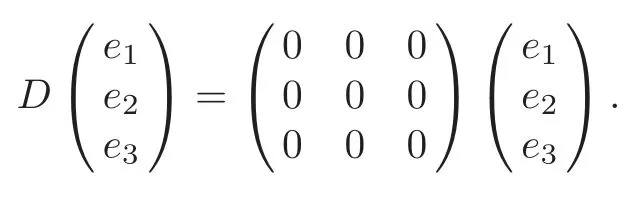
(2) (G3,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if

(i)αβ≠0,γ=0,c=0.In particular,

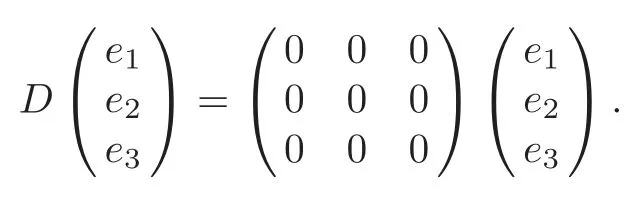
(ii)α=β=γ=0,c≠0.In particular,

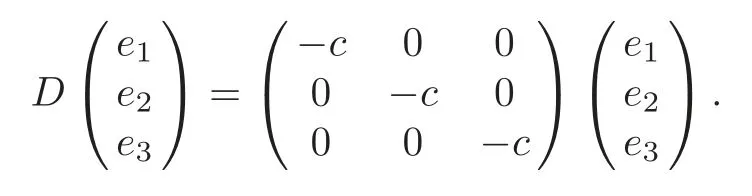
(iii)α=0,γβ+c=0.In particular,

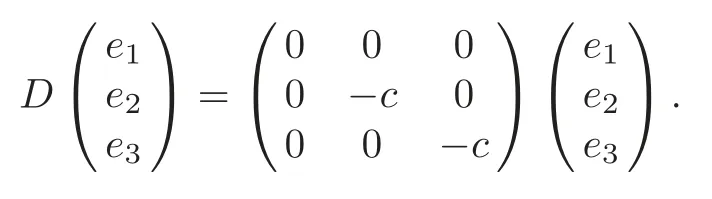
(iv)β=0,γα+c=0.In particular,

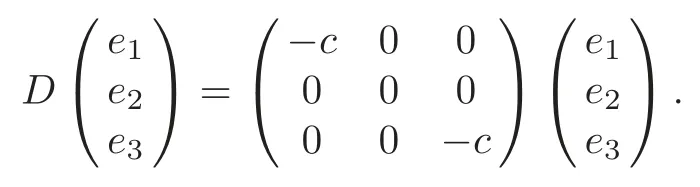
ProofThe canonical connection ∇0of (G3,J) is given by

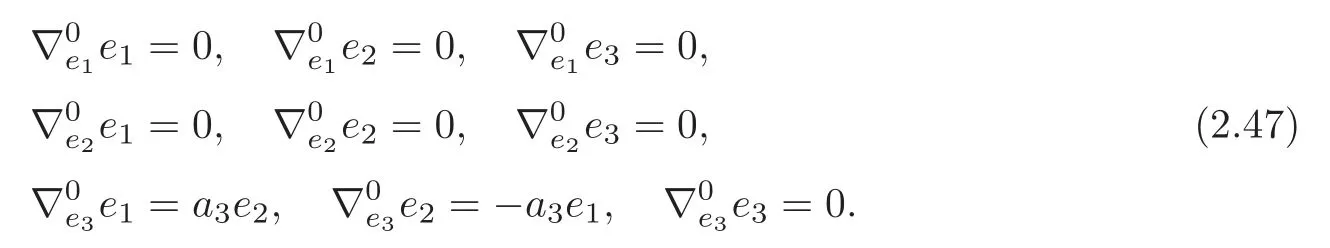
By (2.7) and (2.47),we have the curvatureR0of the canonical connection ∇0of (G3,J) is given by

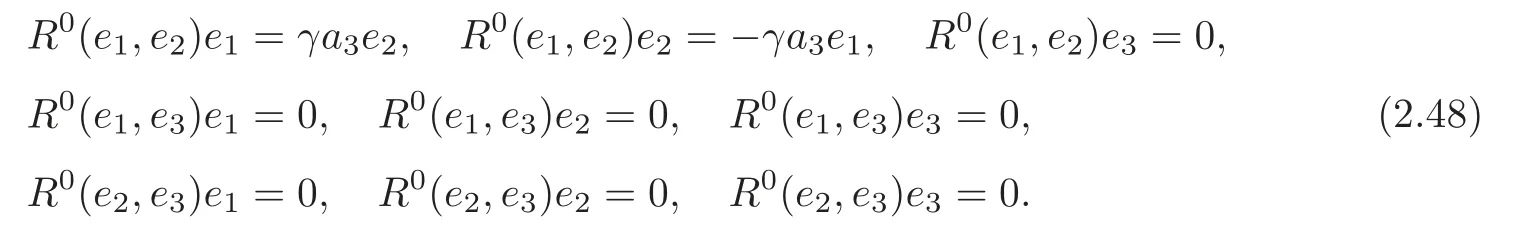
By (2.9),(2.11) and (2.48),we get for (G3,∇0),

If (G3,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

By (2.15) and (2.50),we get the case (1).Similarly the case (2) holds.

By[1,Lemma 3.11],we have that forG4,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG4satisfies

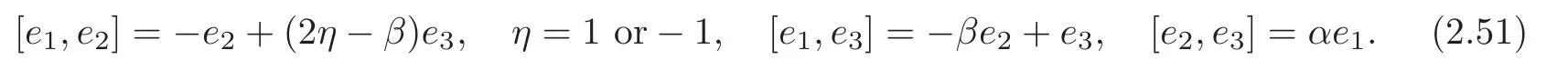
Theorem 2.7(1) (G4,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)α=0,β=1,c=0,η=1.In particular,

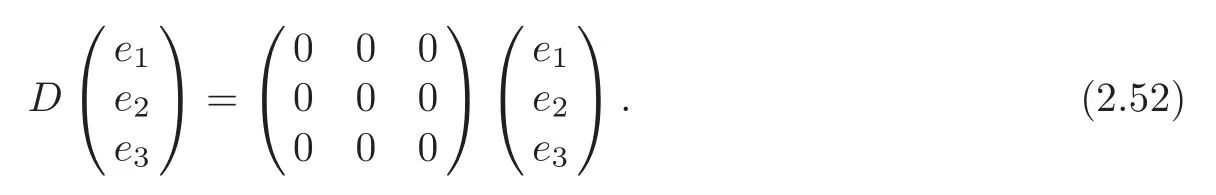
(ii)α=0,c=−1,β=2η.In particular,

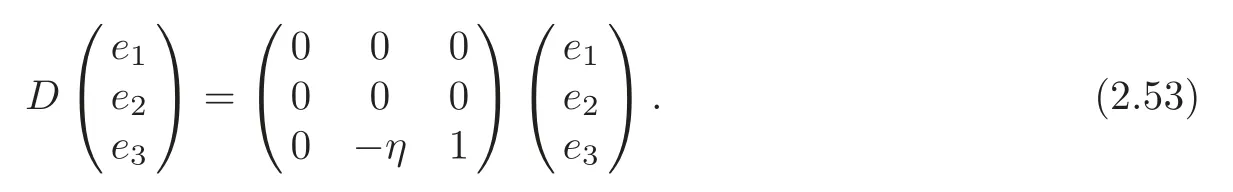
(2) (G4,g,J)is the second kind algebraic Ricci soliton associated to the connection∇0if and only if α=0,β=η,c=0.In particular,

(3) (G4,g,J)is not the first kind algebraic Ricci soliton associated to the connection∇1.

(4) (G4,g,J)is not the second kind algebraic Ricci soliton associated to the connection∇1.

ProofThe canonical connection ∇0of (G4,J) is given by

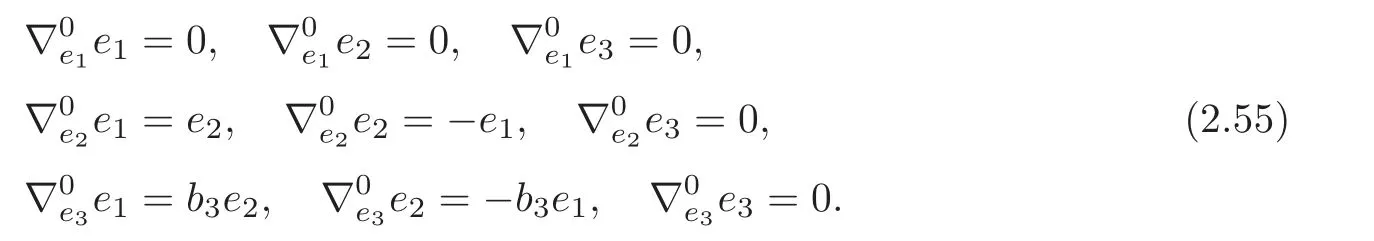
By (2.7) and (2.55),we have the curvatureR0of the canonical connection ∇0of (G4,J) is given by

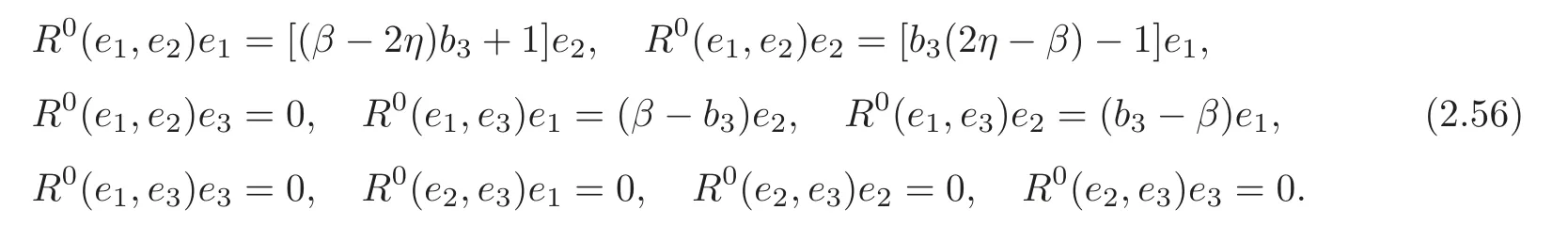
By (2.9),(2.11) and (2.56),we get for (G4,∇0),

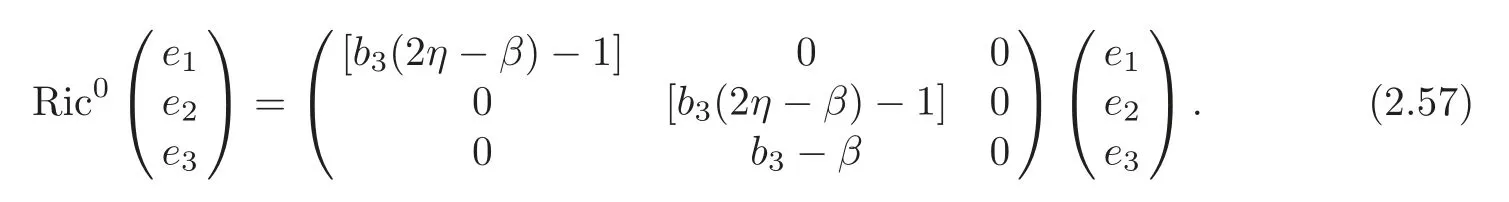
If (G4,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

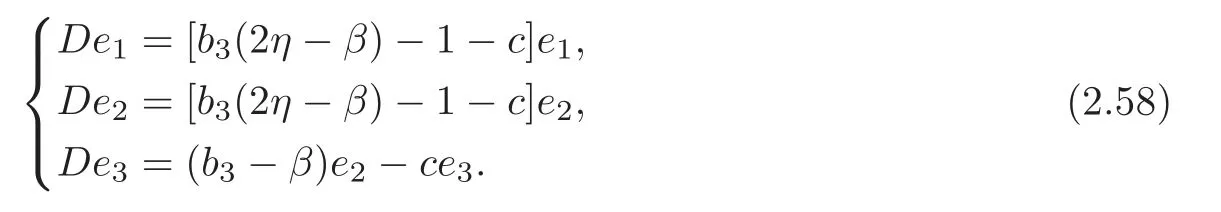
By (2.15) and (2.58),we get

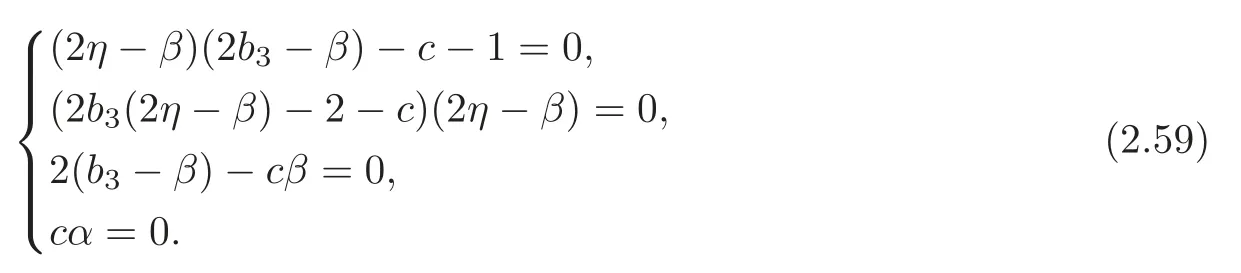
Solving (2.59),we get the case (1).The other cases hold similarly.

By[1,Lemma 4.1],we have that forG5,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG5satisfies

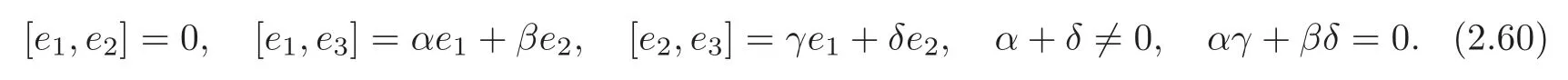
Theorem 2.8(1) (G5,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if c=0.In particular,

(2) (G5,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if c=0.In particular,

ProofThe canonical connection ∇0of (G5,J) is given by

By (2.7) and (2.63),we have that the curvatureR0of the canonical connection ∇0of (G5,J)is flat,that isR0(ei,ej)ek=0.So we get for (G5,∇0),

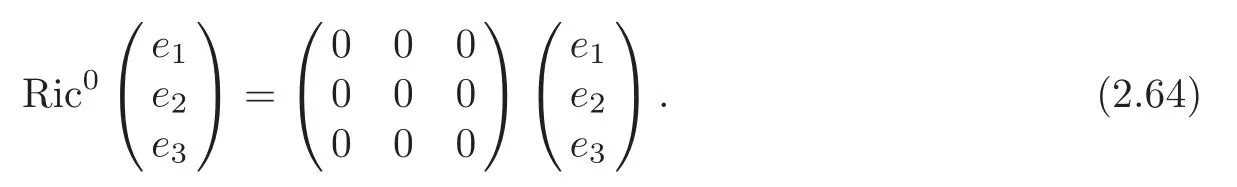
If (G5,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

By (2.15) and (2.65),we get the case (1).Similarly the case (2) holds.

By[1,Lemma 4.3],we have that forG6,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG6satisfies

Theorem 2.9(1) (G6,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)α=β=γ=c=0,δ≠0.In particular,

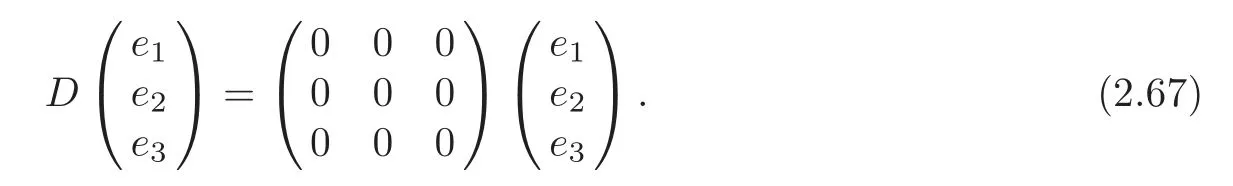
(ii)α≠0,β=γ=0,α2+c=0,α+δ≠0.In particular,

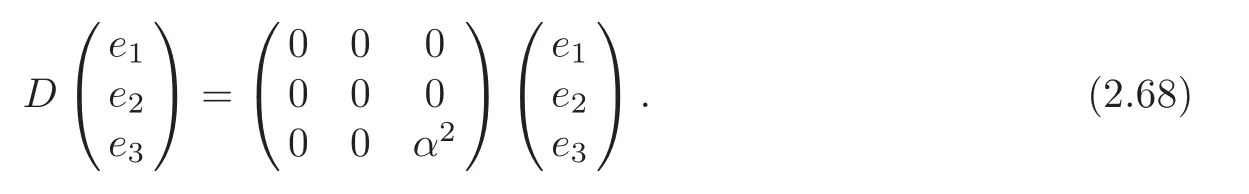
(iii)α≠0,β≠0,γ=δ=0,β2=2α2,c=0.In particular,

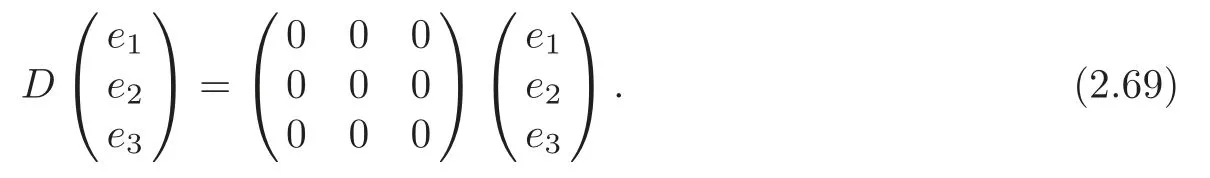
(2) (G6,g,J)is the second kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)β=γ=0,α2+c=0,α+δ≠0.In particular,

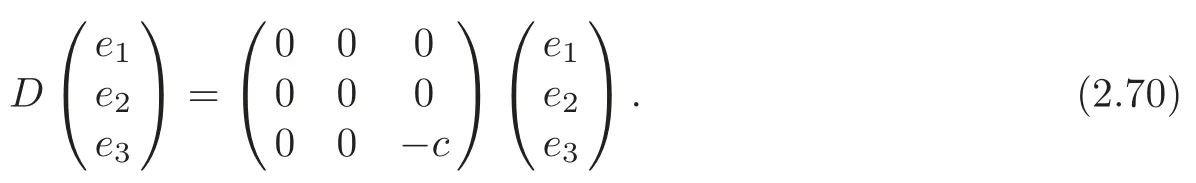
(ii)γ=δ=c=0,α≠0,β≠0,β2=2α2.In particular,

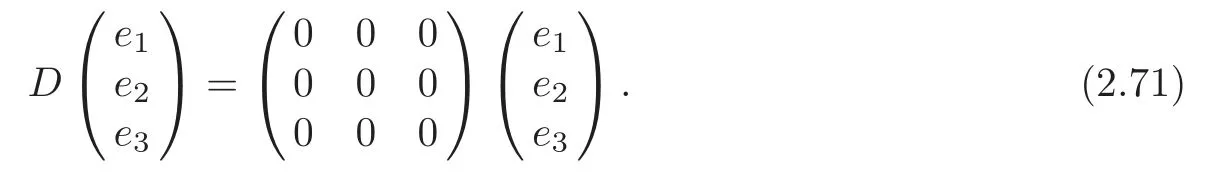
(3) (G6,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if

(i)α=β=c=0,δ≠0.In particular,

(ii)α≠0,β=γ=0,α2+c=0,α+δ≠0.In particular,

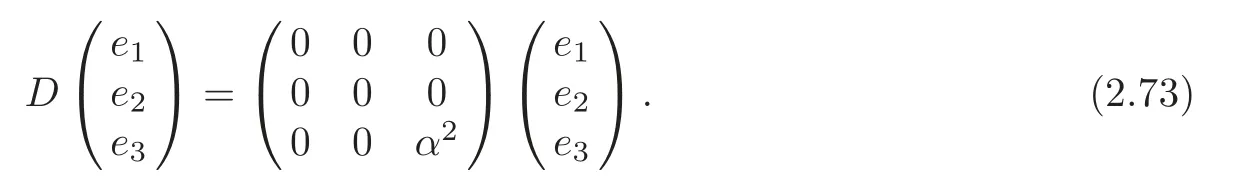
ProofThe canonical connection ∇0of (G6,J) is given by

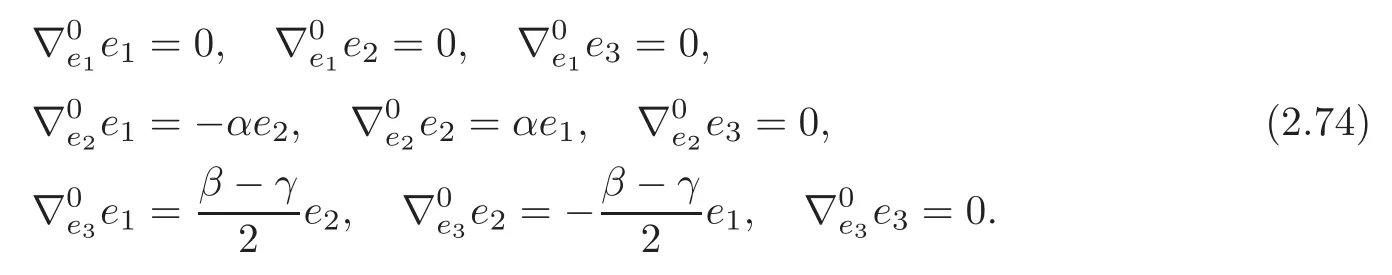
By (2.7) and (2.74),we have that the curvatureR0of the canonical connection ∇0of (G6,J)is given by

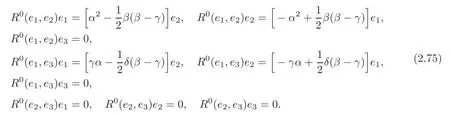
By (2.9),(2.11) and (2.75),we get for (G6,∇0),

If (G6,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

By (2.15) and (2.77),we get

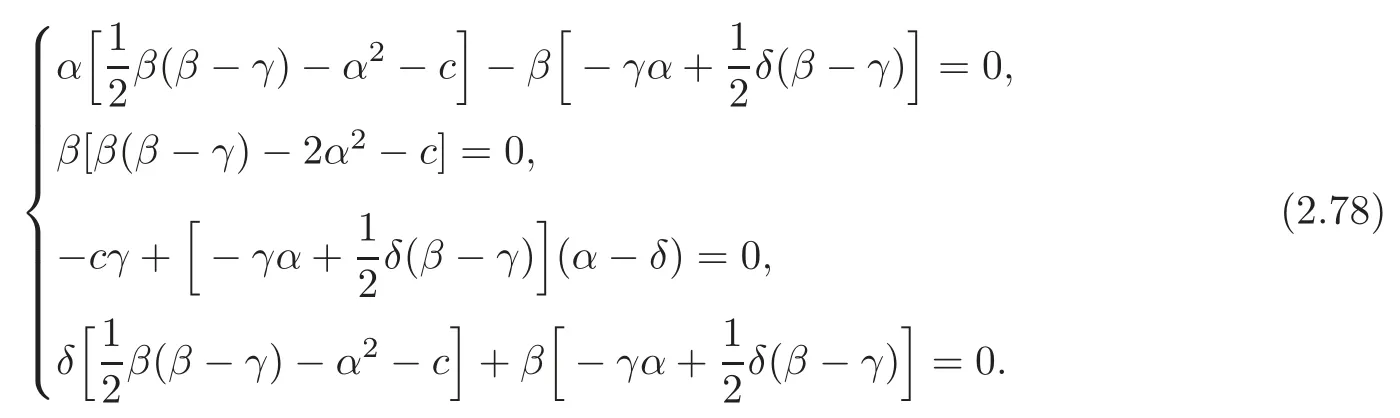
Solving (2.78),then the case (1) holds.The other cases hold similarly.

By[1,Lemma 4.5],we have that forG7,there exists a pseudo-orthonormal basis{e1,e2,e3}withe3timelike such that the Lie algebra ofG7satisfies

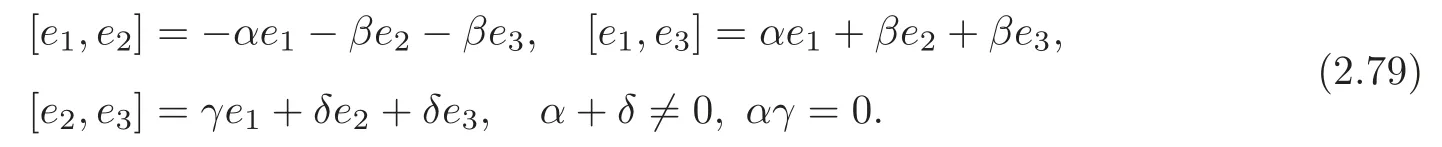
Theorem 2.10(1) (G7,g,J)is the first kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)α=γ=c=0,β≠0,δ≠0.In particular,

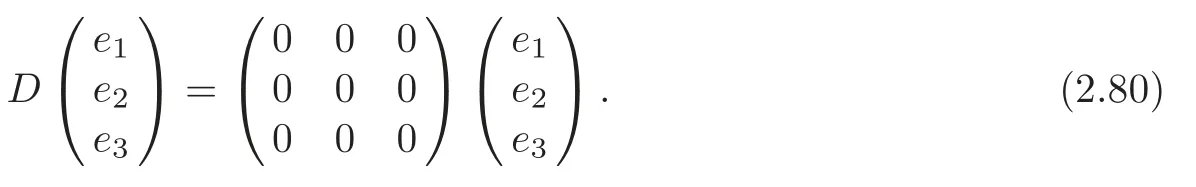
(ii)β=γ=0,α2+c=0,α+δ≠0.In particular,

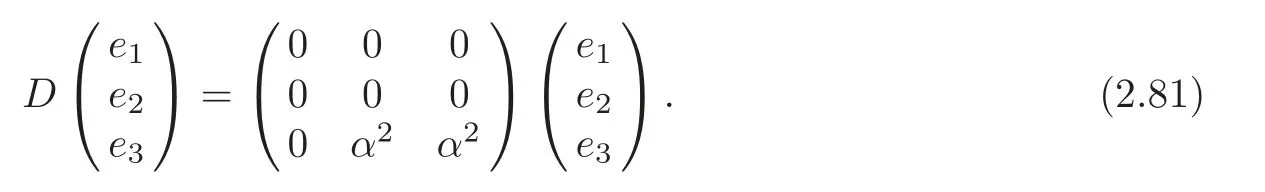
(2) (G7,g,J)is the second kind algebraic Ricci soliton associated to the connection∇0if and only if

(i)α=γ=c=0,δ≠0.In particular,

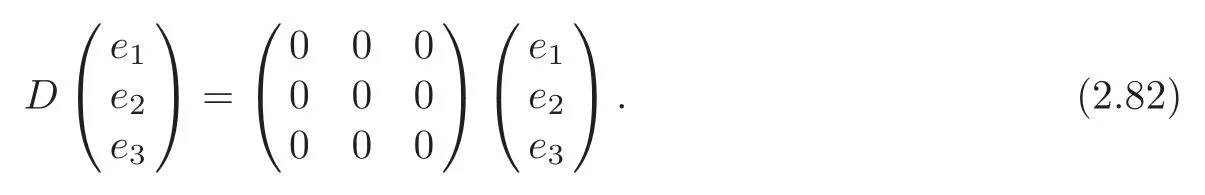
(ii)α≠0,β=γ=0,+c=0,α+δ≠0.In particular,

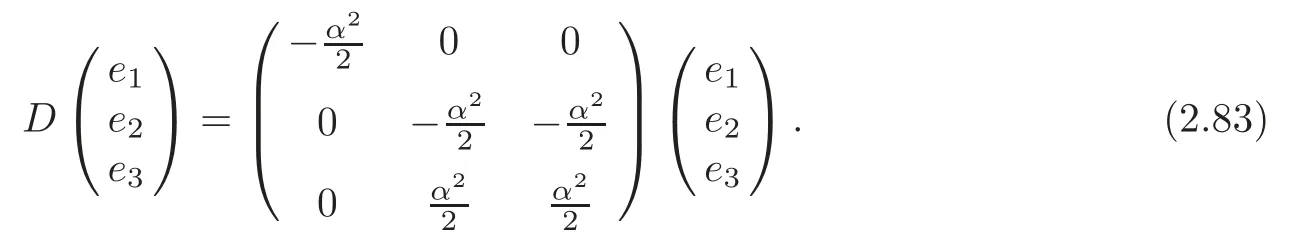
(3) (G7,g,J)is the first kind algebraic Ricci soliton associated to the connection∇1if and only if α≠0,β=γ=0,α=2δ,c=−3δ2.In particular

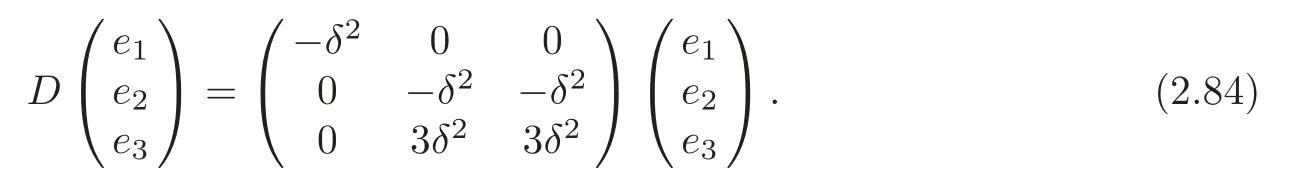
(4) (G7,g,J)is the second kind algebraic Ricci soliton associated to the connection∇1if and only if α≠0,β=γ=0,α=2δ,α2+2c=0.In particular

ProofThe canonical connection ∇0of (G7,J) is given by

By (2.7) and (2.86),we have that the curvatureR0of the canonical connection ∇0of (G7,J)is given by

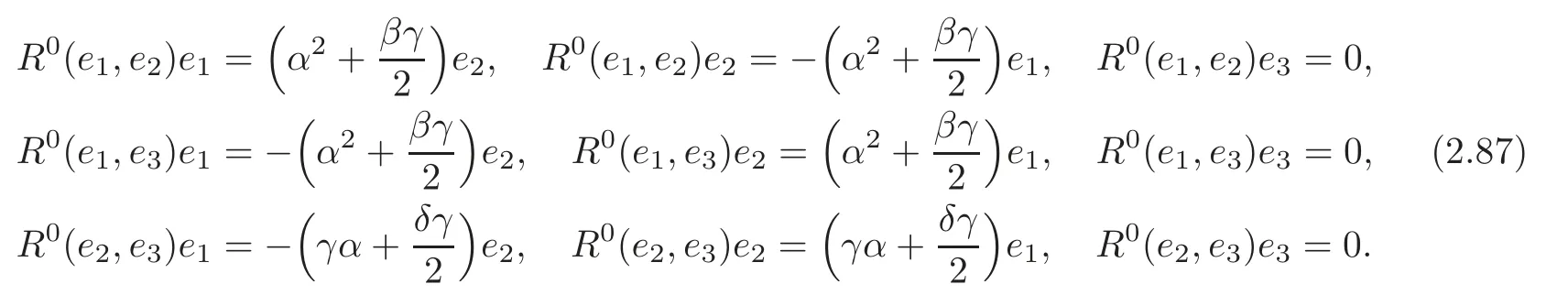
By (2.9),(2.11) and (2.87),we get for (G7,∇0),

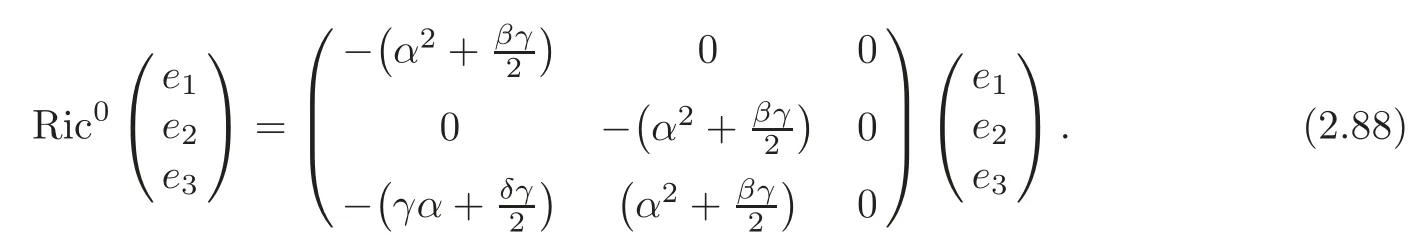
If (G7,g,J) is the first kind algebraic Ricci soliton associated to the connection ∇0,then Ric0=cId+D,so

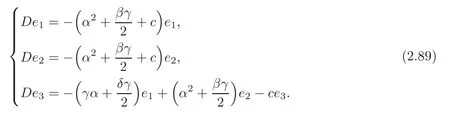
By (2.15) and (2.89),we get

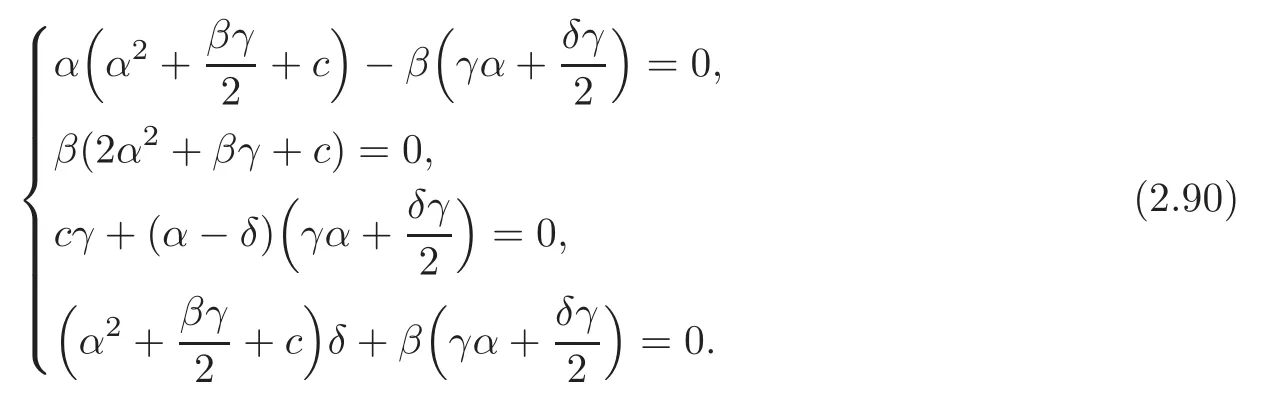
Solving (2.90),we get the case (1).The other cases hold similarly.

AcknowledgementThe author would like to thank the referees for their careful reading and helpful comments.