Four Families of Nontrivial Product Elements in the Stable Homotopy Groups of Spheres∗
2022-07-08LinanZHONGJianguoHONGHaoZHAO
Linan ZHONG Jianguo HONG Hao ZHAO
1Department of Mathematics,Yanbian University,Yanji 133002,Jilin,China.E-mail: lnzhong@ybu.edu.cn
2Sino-European Institute of Aviation Engineering,Civil Aviation University of China,Tianjin 300300,China.E-mail: 39919203@qq.com
3Corresponding author.School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China.E-mail: zhaohao@scnu.edu.cn
Abstract In this paper,the authors introduce a new effective method to compute the generators of the E1-term of the May spectral sequence.This helps them to obtain four families of non-trivial product elements in the stable homotopy groups of spheres.
Keywords Stable homotopy groups of spheres,Adams spectral sequence,May spectral sequence
1 Introduction
LetSbe the sphere spectrum localized at an odd primepand A be the modpSteenrod algebra.To determine the stable homotopy groups of spheresπ∗Sis one of the central problems in homotopy theory.Up to now,several methods have been found to approach it.For example,we have the classical Adams spectral sequence(ASS for short)(see [1])(Zp,Zp) based on the Eilenberg-Maclane spectrumKZp,whoseE2-term is the cohomology of A.Thus in order to compute the stable homotopy groups of spheres with the classical ASS,we need to compute theE2-term of the Adams spectral sequence.We also have the Adams-Novikov spectral sequence(ANSS for short) (see [1,11]) based on the Brown-Peterson spectrumBP.
Letq=2(p−1) andMbe the modpMoore spectrum given by the cofibration

Letα:be the Adams map andV(1) be its cofibre given by the cofibration

LetV(2) be the cofibre ofβ:given by the cofibration
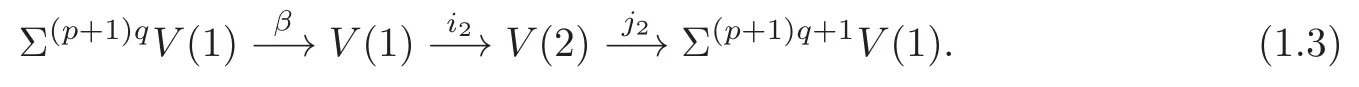
LetV(3) be the cofibre ofγ:given by the cofibration

Especially,the composite
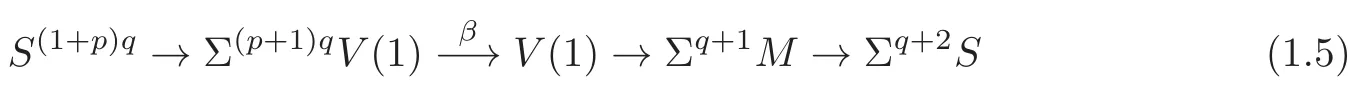
isβ1∈πpq−2S.In [3],Cohen showed thath0bn−1survives toE∞in the Adams spectral sequence and converges to a non-trivial elementζn∈πpnq+q−3S.By the method of ANSS,Lee[4]showed thatζnis a non-trivial element ofπ∗Sforn≥1,i.e.,h0bnis a permanent cycle in the Adams spectral sequence and converges non-trivially toh0bn.
Fors≥1,we define theα-elementαs=j0αsi0∈πsq−1S,theβ-elementβs=j0j1βsi1i0∈πq(sp+(s−1))−2Sand theγ-elementγs=j0j1j2γsi2i1i0∈πq(sp2+(s−1)p+(s−2))−3S.In[13],it was shown that these three families of elements are represented by then-th Greek letter elementsin the Adams spectral sequence,whereis

where ∧denotes the Yoneda product and(Zp,E(n−1)).By sendingα(sn)back to theE1-term of the May spectral sequence,we see that

Based on the above results,we should naturally ask that whether the product elementα(n)sxfor somex∈(Zp,Zp)converges to a nontrivial element ofπ∗Sor not.In[12],it was shown that the producth0bn−1(n≥2,2≤s≤p−1) is a permanent cycle in the Adams spectral sequence and converges to a nontrivial element of orderpinπ∗S.In [13],Wang-Zheng verified the convergences ofh0hn(p≥5,2≤s≤p−1,n≥2)andh0hn(p≥7,3≤s≤p−1,n≥3).Recently,in [5–6],Liu verified the convergences ofh0hnb0(p >3,n≥3,1
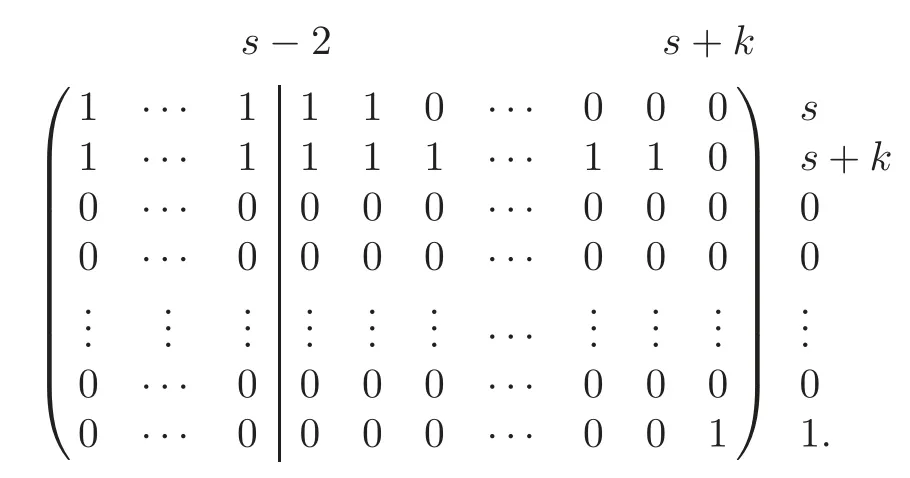
Theorem 1.1(1)Let p>5,k >0,n≥3and s>1.Thenh0hnbk0(3 (2)Let p >7,k >0,n≥4and s >2.Thenh0hnbk0(4 This paper is organized as follows.In Section 2,after recalling some knowledge on the May spectral sequence,we introduce a better method which is used to compute the generators ofE1-term of the May spectral sequence.Then in Section 3,we use this method to give some important results on Ext-groups which are then applied to give the proof of our main Theorem 1.1. It is well known that the most successful method for computing(Zp,Zp) is the May spectral sequences.Let A∗denote the dual algebra of modpSteenrod algebra A.Milnor [10]showed that,as a Hopf algebra whereP[ ]is the polynomial algebra andE[ ]is the exterior algebra.The secondary degrees ofξiandτiare 2(pi−1) and 2(pi−1)+1,respectively.The coproduct ∆: A∗→A∗⊗A∗is given by and Letε: A∗→Z/pbe the argumentation homomorphism and=Kerεwhich is called the argumentation ideal of A∗.It then follows a bigraded cochain complex (C∗,∗(H∗S),d)=(C∗,∗(Z/p),d),whereC∗,∗(Z/p) is the cobar construction withs-filtration and the differential d:Cs,t(Z/p)→Cs+1,t(Z/p) is given by whereλ(i) is the total degree of(refer to[9]).For example,we have differentials According to the above statements,the cohomology ofC∗,∗(Z/p) is which is theE2-term of the ASS.From [8]we know that Based on [11,Theorem 3.2.5],we can set a May filtration on A∗by lettingM(τi−1)=M()=2i−1.It induces a corresponding filtration It was shown that for the associated bigraded Hopf algebra there is an isomorphism whereT[ ]denotes the truncated polynomial algebra of heightpon the indicated generators,τiandξi,jare the projections ofτiand,respectively.Applying the filtration (2.2) to the cobar constructionC∗,∗(Z/p),we obtain a filtration It follows an tri-graded exact couple which induces the so-called May spectral sequence (MSS for short) where dr:Es,t,Mr→Es+1,t,M−rris therthdifferential of the MSS.Since the MSS converges to theE2-term of the ASS,the nontriviality of the elements in(Z/p,Z/p) is equivalent to showing that its representation in the MSS is an infinite cycle. TheE0-term of the MSS isand theE1-termE1=H∗(E0A∗,d0) is isomorphic to where and In the filtrated cobar complexes,hi,j,bi,jandaiare represented by respectively.It is known that the generatorsh1,i,b1,ianda0converge tohi,bi,a0∈(Z/p,Z/p),respectively.In the May spectral sequence,one has ther-th May differentail forx∈andy∈.The first May differential d1is given by There exists the graded commutativity in theE1-term of MSS: For each elementx∈,we define dimx=s,degx=t.Then we have wherei≥1,j≥0. In the follows,we introduce a new method to compute the generators of theE1-term of MSS.According to [15],we denoteai,hi,jandbi,jbyx,yandz,respectively.By the graded commutativity ofwe consider a generator We define the polynomial algebra Then there is the obvious identificationFurthermore,ifbi,jis replaced byhi,j+1,then we get By the graded commutativity of,we can consider a generator Then the generatorgdetermines a matrix where(xi,0,xi,1,···,xi,n)is of the form(1,···,1,0,···,0)and the transposition0)Trepresentsaiin partA.Meanwhile,(yi,0,yi,1,···,yi,n) is of the form (0,···,0,1,···,1,0,···,0) andrepresentshi,jin partB. By the graded commutativity of,matrix (2.5) can always be transformed into a new one by the interchange of columns in partAandBrespectively,and the entriesxi,j,yi,jin the new matrix satisfy the following conditions: By the properties of thep-adic number and the reason of the second degree,we have the following equations whereλi≥0,the integer sequencec=(c0,c1,···,cn) is determined byand the carry sequenceλ=(λ1,λ2,···,λn). We want to get the solutions of (2.7) which satisfy the conditions (2.6).Unfortunately,the matrix solutions do not always detect generators of.In order to achieve our object,we introduce the following diagram which shows our manipulation during computing the generators ofE1-term: where ∗1denotes the resolutionhi,j→hi−k,j+khk,jandai→ai−jhj,i−j,∗2denotes the replacementhi,j+1→bi,j,k≥0,≤s−b. From the discussion above,the determination ofis reduced to the following steps: S2: List up all the possibles of sequenceλin the corresponding sequencec. S3: For each sequencec,we can solve (2.7) which satisfy the conditions (2.6).Thus,we get all generators of. S4: Through replacementhi,j+1→bi,jand resolution we can get all generators of. In what follows,we will apply the above method to compute the generators of certainE1-terms of MSS.For convenience,we writet1=pnq+(s+k)pq+sqandt2=pnq+sp2q+(s+k−1)pq+(s−1)qwithk >0. Proposition 2.1Let p>5and n≥3.Then we have (1)for s>1,3 (2)for s>1,4 Proof(1) Consider the generatorg∈for 1≤r≤s+2k+2,wheret1=pnq+(s+k)pq+sqwith Then we have dimg=s+2k+2−rand degg=t1+(s−r−1). Ifs−1 Sinces+2k+2−r Case 1.1r=1.Solve (2.7) by virtue of (2.6),we get the following matrix: Case 1.2r≥2.Similar to Case 1.1,we detect the generator Combining Cases 1.1 and 1.2 gives the desired result. (2) Similar to (1),we consider the generator for 1≤r≤s+2k+2,wheret1=pnq+(s+k)pq+sqwith Then we have dimg=s+2k+3−rand degg=t1+(s−r−1).From (2.7),one can easily get the carry sequence and correspondinglyc=(s,s+k,0,···,0). Case 2.1r=1.Solve (2.7) by virtue of (2.6),we get the generator By the resolutionh2,0→h1,1h1,0,we get the generator Case 2.2r≥2.Similar to Case 2.1,we detect the generatorBy the replacementhk1,1→bk1,0andh2,0→h1,1h1,0,we get the generatorwhich is zero for Combining Case 2.1 with Case 2.2 gives the desired result. Proposition 2.2Let p>7,n≥4and s>2.Then we have (1)for4 (2)for5 Proof(1) Consider the generatorg∈for 1≤r≤s+2k+2.Then we have Meanwhile,we have dimg=s+2k+2−rand degg=t2+(s−r−2).One can easily gets−r−2≥0. Sinces+ 2k+ 2−r Case 1.1r=1.Solving(2.7)by virtue of(2.6)deduces three possiblek−1 rows as follows: If we choose (1) as the third row,then we obtain the following matrix: It detects the generator By the resolutionh3,0→h1,2h2,0,we get the generator By the resolutionh2,0→h1,1h1,0,we get the generator If we choose (2) as the third row,then we get the following matrix: It detects the generator By the resolutionh2,0→h1,1h1,0andh3,0→h2,1h1,0orh1,2h2,0,we get the generator and which are both zeroes due to=0 and=0 in.Thus suchgis impossible to exist. Similarly,if we choose(3)–(k-1)as the third row,respectively,it is easy to know thatgdoes not exist either. Case 1.2r≥2.Sincexi≤s−r−2≤s−4<=s−1,the first equation of (2.7)has no solution.Thus suchgis impossible to exist. Combining Cases 1.1 and 1.2 gives the desired result. (2)Consider the generatorg∈for 1≤r≤s+2k+2.Then we have(,···,)=(s−1,s+k−1,s,0,···,0,1).Meanwhile,there is dimg=s+2k+3−rand degg=t2+(s−r−2)withs−r−2≥0.Sinces+2k+3−r Case 2.1r=1.Similar to Case 1.1 in Proposition 2.2(1),solving (2.7) by virtue of (2.6)follows the generator By the resolutionh3,0→h1,2h2,0→h1,1h1,0h1,2,we get the generator Case 2.2r≥2.Sincexi≤s−r−2≤s−4 Combining Case 2.1 with Case 2.2 gives the desired result. In this section,we give some results on Ext-groups which will be used in the proof of the main theorem.For simplicity,we still lett1=pnq+(s+k)pq+sqandt2=pnq+sp2q+(s+k−1)pq+(s−1)qwithk >0. Lemma 3.1Let p>5,n≥3and s>1.Then we have (1)when3 (2)when4 Proof(1) It is known thath1,0,h1,n(n≥0),are permanent cocycles and converge nontrivially toh0,hn(n≥0),respectively.It follows that is a permanent cocycle in the May spectral sequence and converges to According to Proposition 2.1(1),we have which followsis trivial forr≥1.Thus the permanent cycle cannot be hit by any differential in the May spectral sequence.Thus Whenr≥2,by Proposition 2.1(1),we see thatis trivial.It follows that (2)In the May spectral sequenceare permanent cocycles and converge nontrivially toforn≥0,respectively.It follows that is a permanent cocycle in the May spectral sequence and converges to According to Proposition 2.1(2),contains one generator Since Whenr≥2,by Proposition 2.1(2),we see thatis trivial.It follows that Lemma 3.2Let p>7,n≥4and s>2.Then we have (1)when4 (2)when5 Proof(1) It is known thatare permanent cocycles and converge nontrivially toh0,hn(n≥0),bk0andrespectively.It follows that is a permanent cocycle and converges toin the May spectral sequence. According to Proposition 2.2(1),there is one generator Since Forr≥2,according to Proposition 2.2(1),we have Thus (2)In the May spectral sequenceare permanent cocycles and converge nontrivially toh0,bn−1(n≥0),bk0andrespectively.It follows that is a permanent cocycle and converges toin the May spectral sequence. According to Proposition 2.2(2),there is one generator Since Forr≥2,according to Proposition 2.2(2),we have Thus In what follows,we give the proof of our main theorem. Proof of Theorem 1.1(1)It is well known thatb0∈(Zp,Zp)is a permanent cycle in the Adams spectral sequence and converges nontrivially to theβ-elementβ1=j0j1βi1i0∈πpq−2S.From [3],(i0)∗(h0hn) ∈(H∗M,Zp) is a permanent cycle in the Adams spectral sequence and converges to a non-trivial elementξn∈πpnq+q−2(M).Therefore the following composite is represented up to nonzero scalar by in the Adams spectral sequence. By using the Yoneda products,we know that the composite is a multiplication by Hence (j0j1βsi1i0)∗(h0hn)βk1is represented by in the Adams spectral sequence. Similarly,by the virtue of the convergence ofh0bn−1(see [3]) and Lemma 3.1(1),we can get thatsurvives non-trivially to a homotopy element ofπ∗S. (2) Consider the following composite is represented up to nonzero scalar by in the Adams spectral sequence.By using the Yoneda products,we know that the composite is a multiplication by Hence the composite (j0j1j2γsi2i1i0)∗(h0hn)βk1is represented by in the Adams spectral sequence. By virtue of the convergence ofh0bn−1(see [3]) and Lemma 3.2(2),we see thatsurvives non-trivially to a homotopy element ofπ∗S. AcknowledgementThe authors would like to give their thanks to the referee for his/her many helpful suggestions on the original version of this paper.2 Detecting Generators in E1-Term of MSS
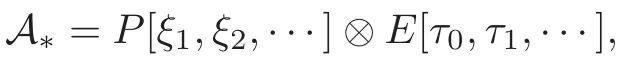
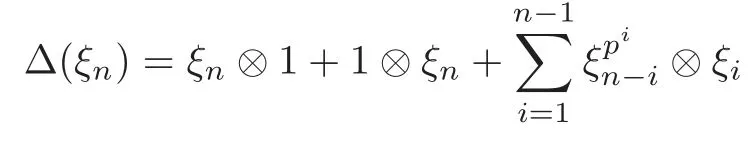

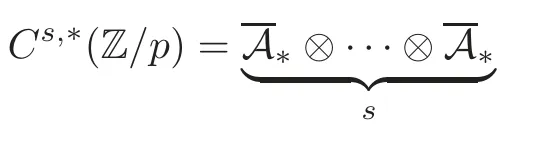
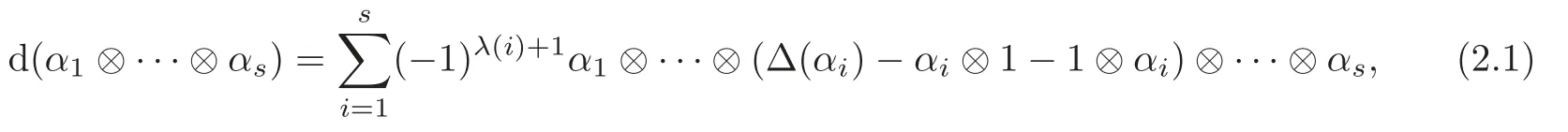

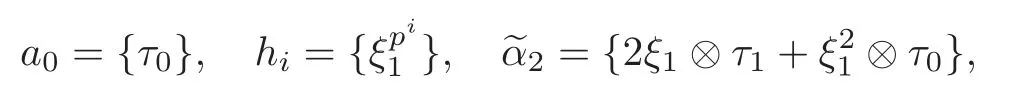
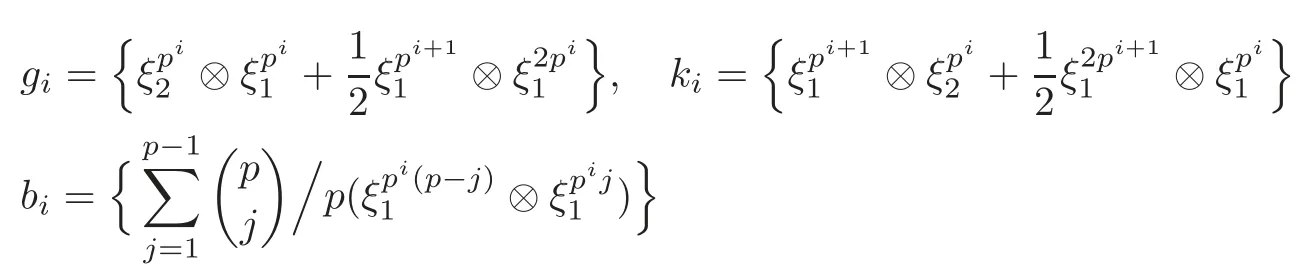

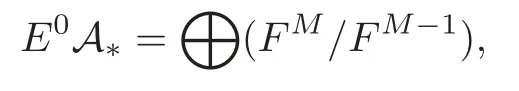

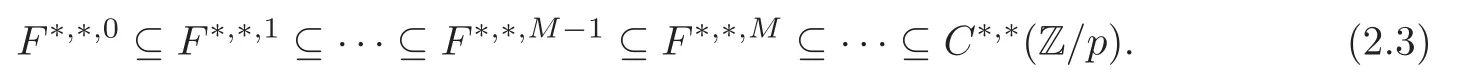
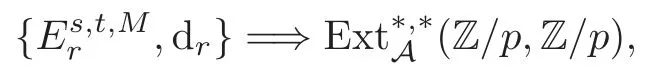





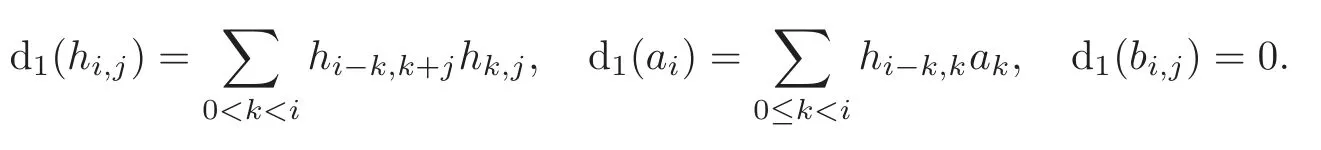

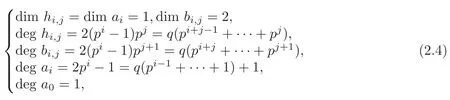

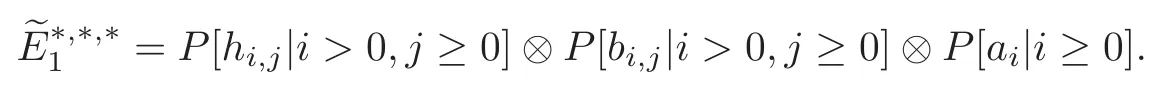

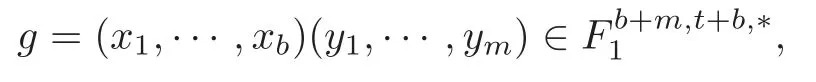
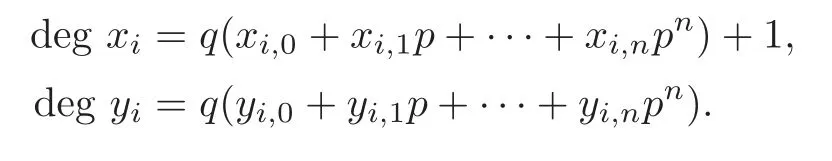

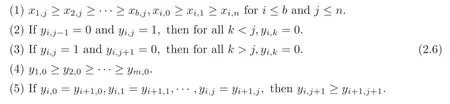


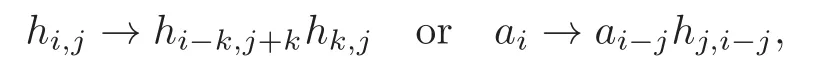

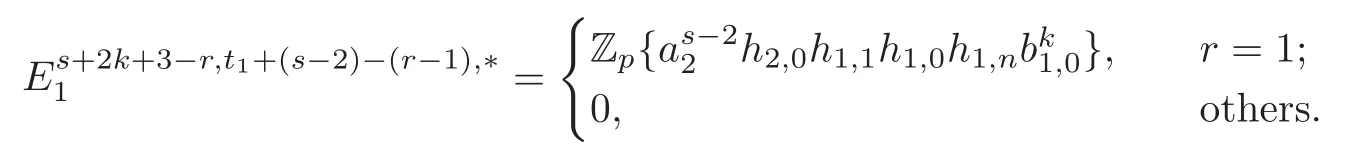


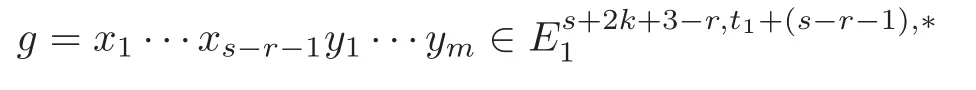

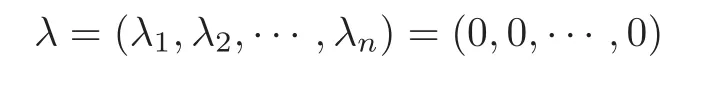
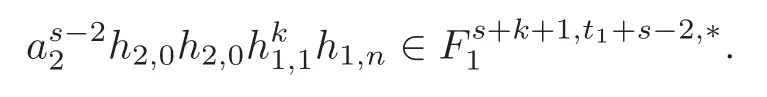

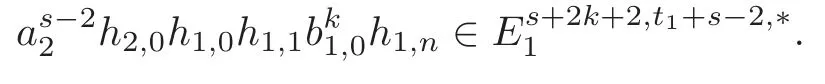

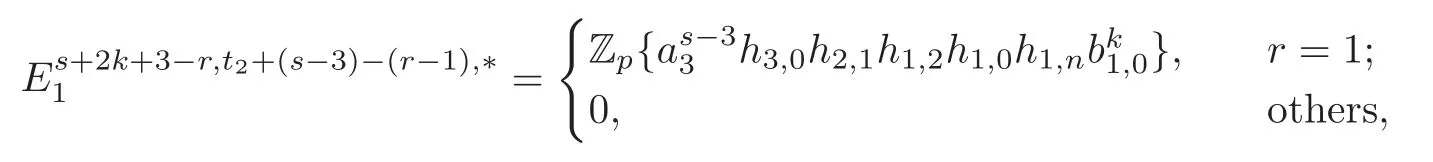
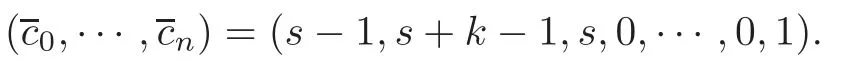





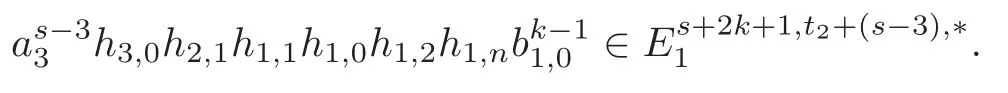


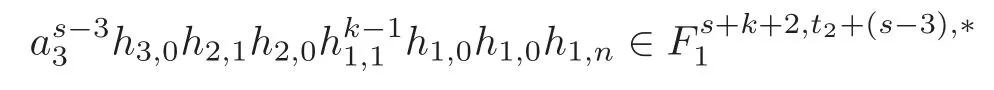

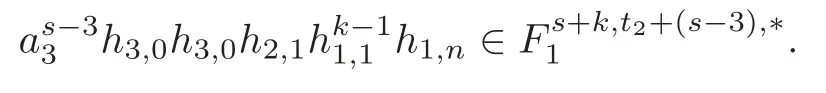

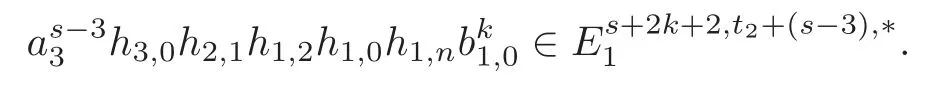
3 Proof of Theorem 1.1


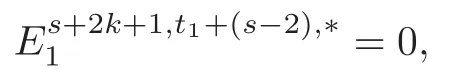
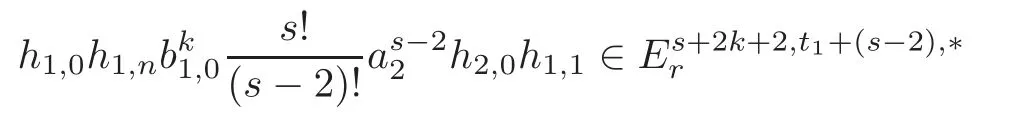
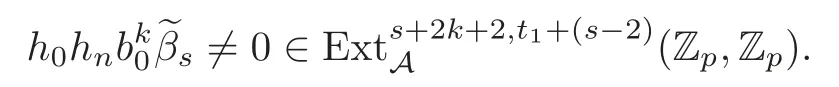

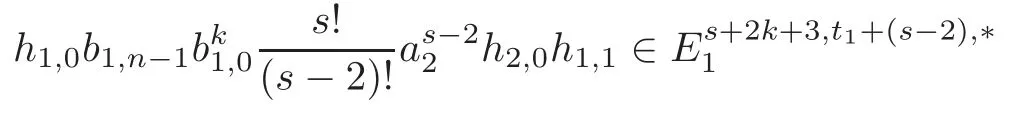

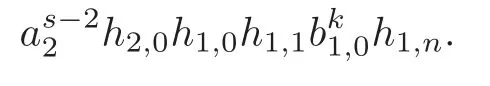
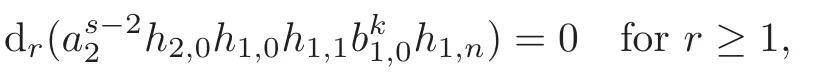
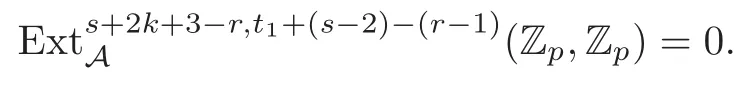


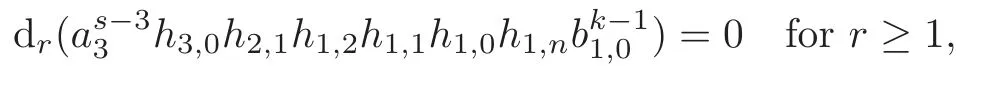
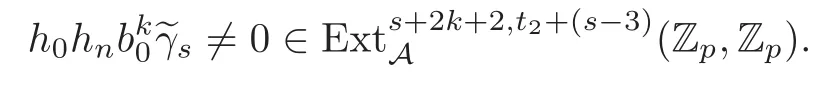
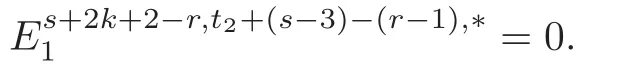
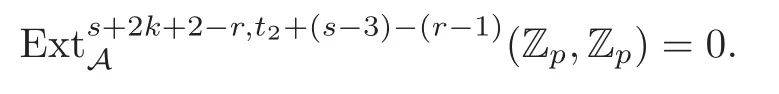
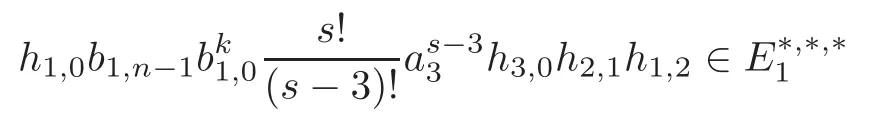
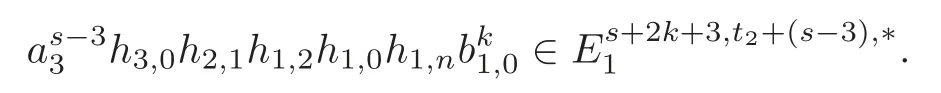
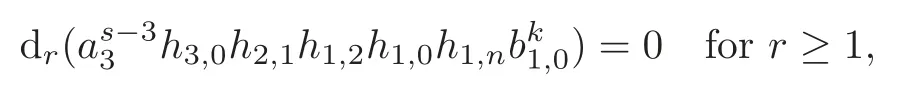


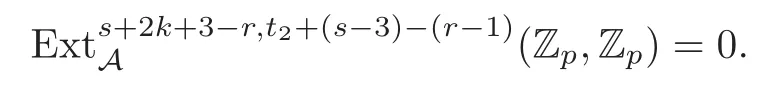

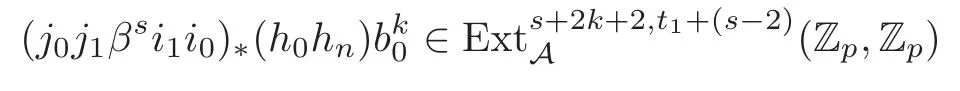
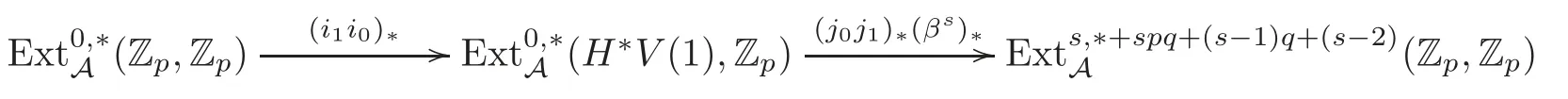

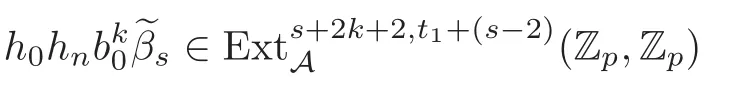
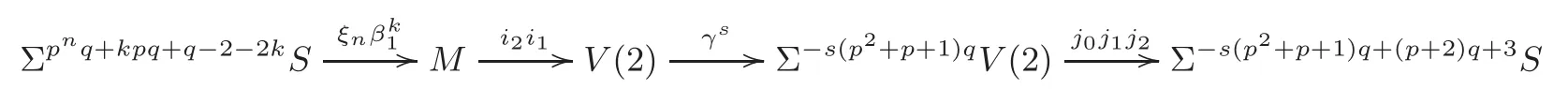
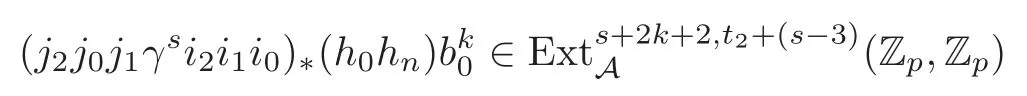


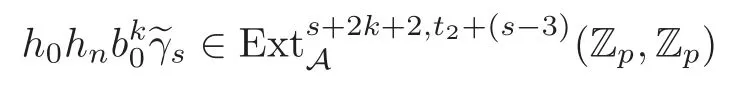
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- A Characterization of the Standard Tori in C2 as Compact Lagrangian ξ-Submanifolds∗
- Canonical Connections and Algebraic Ricci Solitons of Three-dimensional Lorentzian Lie Groups∗
- Critical Trace Trudinger-Moser Inequalities on a Compact Riemann Surface with Smooth Boundary∗
- On a Supercongruence Conjecture of Z.-W.Sun∗
- Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗
- Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗
