Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗

Huixin DAI Tingbin CAO Yezhou LI

1School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China.E-mail: hxdai@bupt.edu.cn

2Department of Mathematics,Nanchang University,Nanchang,Jiangxi 330031,China.E-mail: tbcao@ncu.edu.cn

3Corresponding author.School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China.E-mail: yezhouli2019@outlook.com

Abstract Let f: C→Pn be a holomorphic curve of order zero.The authors establish a Jackson difference analogue of Cartan’s second main theorem for the Jackson q-Casorati determinant and introduce a truncated second main theorem of Jackson difference operator for holomorphic curves.In addition,a Jackson difference Mason’s theorem is proved by using a Jackson difference radical of a polynomial.Furthermore,they extend the Mason’s theorem for m+1 polynomials.Some examples are constructed to show that their results are accurate.

Keywords Jackson difference operator,Nevanlinna theory,Holomorphic curve,Cartan’s second main theorem,Mason’s theorem,Polynomial

1 Introduction

In the 1980s,an intensive and somewhat surprising interest in the subject reappeared in many areas of mathematics and applications including mainly new difference calculus,orthogonal polynomials and variationalq-calculus(see[10]).In 1908,Jackson investigated the Jackson difference operator (or calledq-derivative) and studied theq-difference equations.These polynomials,the Jackson difference operator and related topics have found numerous applications,such asq-hypergeometric series (see [10]),boundary value problems ofq-difference equations(see [24]).

Recently,there has been a renewed interest in the difference analogues and Jackson difference operator.In 2006,Halburd and Korhonen [12]introduced thec-difference operator:∆cf=f(z+c)−f(z),and got thec-difference analogue of the second main theorem for meromorphic functions in the complex plane.In 2014,Korhonen and Tohge [13]extended the results ofc-difference analogue to holomorphic curves intersecting hyperplanes in general position.Meanwhile,many scholars investigated the value distribution theory ofq-difference analogue in several complex variables (see [5–7]).For the Jackson difference operator,Li and Song [18]considered the functional and dynamical properties.Cao,Dai and Wang [4]studied the Nevanlinna theory of Jackson difference operator and the solutions ofq-difference equations.In this paper,we study the Cartan’s second main theorem of Jackson difference operator and a Jackson difference analogue of Mason’s theorem (see [14,21]).

This paper is organised as follows.In Section 2 we will give some basic notations of Cartan characteristic function and Jackson difference operator theory.Section 3 contains a Jackson difference analogue of the second main theorem for holomorphic curves.Here we introduce a Jackson difference counterpart of the radical,and use it to prove a truncated version of the Cartan’s second main theorem for Jackson difference operator.In Section 4,we state a Jackson difference analogue of Mason’s theorem and extend it form+1 polynomials.In addition,the sharpness of the obtained results is discussed with the help of examples.

2 Preliminaries

2.1 First we recall some known properties of the Cartan characteristic function from [8,11,13,17,20].The order of growth of a holomorphic curveg: C→Pnwith homogeneous coordinatesg=[g0:···:gn]is defined by

where log+x=max{0,logx}for allx≥0.If the functionsgj(j=0,···,n)are entire functions without common zeros,theng=[g0:···:gn]withn≥1 is called the reduced representation ofg.The Cartan characteristic function ofgis

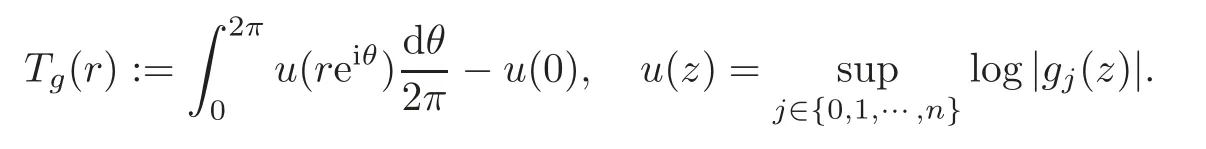
Moreover,iff0,···,fqare linear combinations ofg0,···,gn,and satisfy that anyn+1 of the functionsf0,···,fqare linearly independent over C,q >n,then

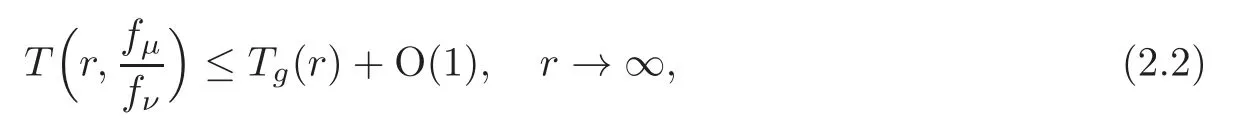
whereµandνare distinct integers in the set{0,···,q}.Especially,ifn=1,then(2.2)becomes an asymptotic identity.For more detailed concepts of Nevanlinna theory and Cartan’s value distribution theory,we can refer to [9,13,17,20,23].

2.2 The Jackson difference operator

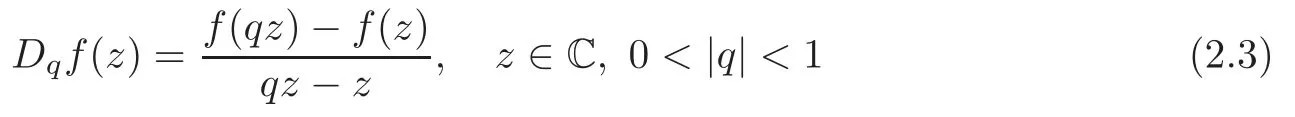
was initially investigated by Jackson [15–16]in 1908.In [4],Cao,Dai and Wang studied the Nevanlinna theory of Jackson difference operator on the complex plane.For a positive integerk∈N,the Jacksonkth-order difference operator is denoted by

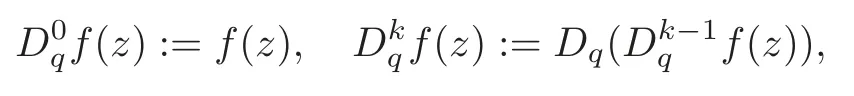
it follows from the equality [1,page 13],

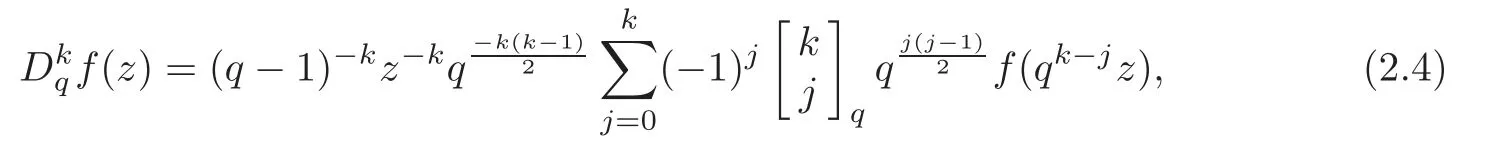
where

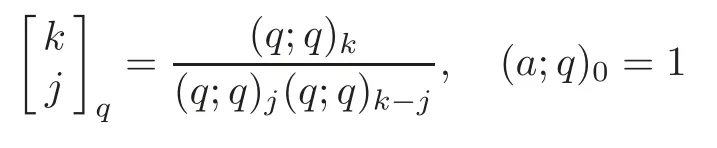
and

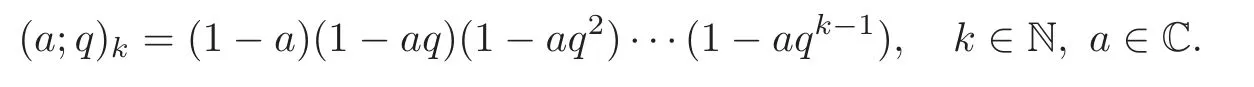
In addition,we can find more notations about Jackson difference operator in [4].

Letf(z) be a non-constant meromorphic function of zero order andq∈C{0,1}. Theqdifference operator ∆qf(z):=f(qz)−f(z) is defined by Barnett [2].Thus by the definition of Jackson difference operator,we can easily show that

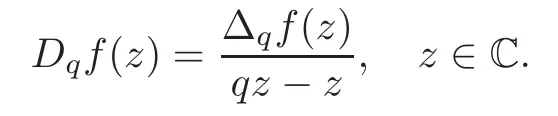
The Wronskian determinant is indispensable in the proof of the Cartan’s generalization of the main second theorem.In [13],aq-difference analogue of Cartan’s result where the ramification term has been replaced by a quantity was expressed in terms of theq-Casorati determinant of functions which are linearly independent over a field.Theq-Casorati determinant (see [13]) is defined by

Similarly,we denote by

the Jacksonq-Casorati determinant ofg0,···,gn.

In fact,we can get the relationship between Cq(g0,g1,···,gn) and CJ(g0,g1,···,gn):

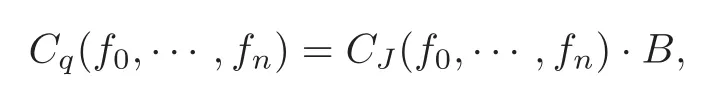
where

We will give it a concrete proof in Lemma 3.1.

2.3 In order to obtain a truncated version of the second main theorem for Jackson difference operator,we introduce the following definitions.

As in [9,14],denote by ordζ(f)=µ∈Z the order of a meromorphic functionfatζ∈C if

As we all know,ordζ(f)>0 implies thatfhas a zero of order ordζ(f)>0 atζ,and ordζ(f)<0 implies thatfhas a pole of order−ordζ(f) atζ.We also adopt the notation ord+ζ(f)=max{0,ordζ(f)} and ord−ζ(f)=max{0,−ordζ(f)}.For the closed disc(z0,s)={z∈C:|z−z0|≤s},we define

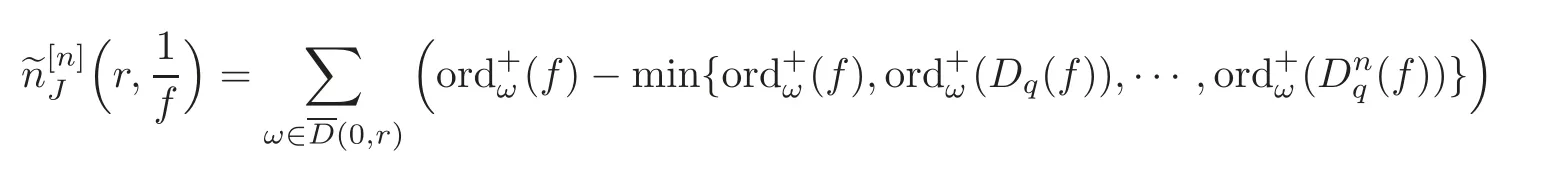
as a Jackson difference analogue of the truncated counting function for the zeros off.The corresponding integrated counting function is defined as

wheren∈N,q∈C{0,1}.

3 Jackson Difference Analogue of Cartan’s Second Main Theorem

Before describing Theorem 3.1,we give a few other remarks.Letfbe a non-constant zeroorder meromorphic function,andq∈C{0,1}. We denote by P0qthe field of meromorphic functions which have forward invariant preimages underfwith respect to the rescalingτ(z)=qz,that isf(qz)≡f(z).In particular,if|q|<1,then for anyf∈P0q,fis a constant.Besides,we set meromorphic function

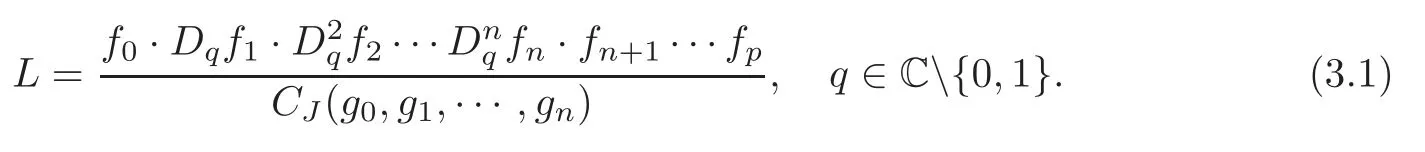
We are now ready to state the Jackson difference analogue of Cartan’s second main theorem.

Theorem 3.1Let g=[g0:···:gn]: C→Pnbe a holomorphic curve with σ(g)=0,g0,···,gn(n≥1)are entire functions without common zeros,linearly independent overP0q,and z∈C{0}.Suppose f0,···,fpare linear combinations of the functions g0,···,gn(p>n),such that any n+1of the functions f0,···,fpare linearly independent.L satisfies(3.1),then

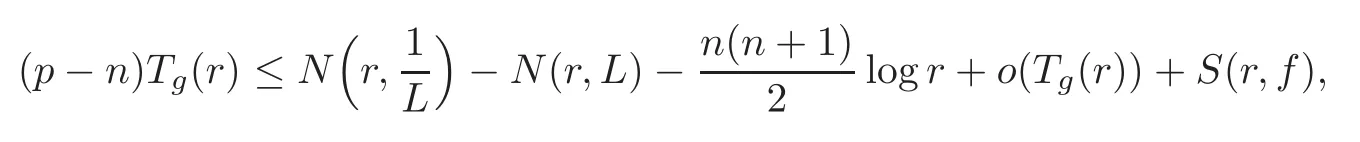
where S(r,f)=o(T(r,fj)),j=0,···,p and r approaches infinity on a set of logarithmic density1.

To prove Theorem 3.1,it suffices to introduce some lemmas.The first lemma is that the relationship between Cq(g0,g1,···,gn) and CJ(g0,g1,···,gn).

Lemma 3.1Let g0,···,gnbe entire functions,n>1,q∈C{0,1}.Then

where

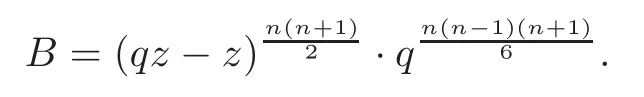
ProofIt follows from the definition of CJ(g0,g1,···,gn) andDkqgkthat

where

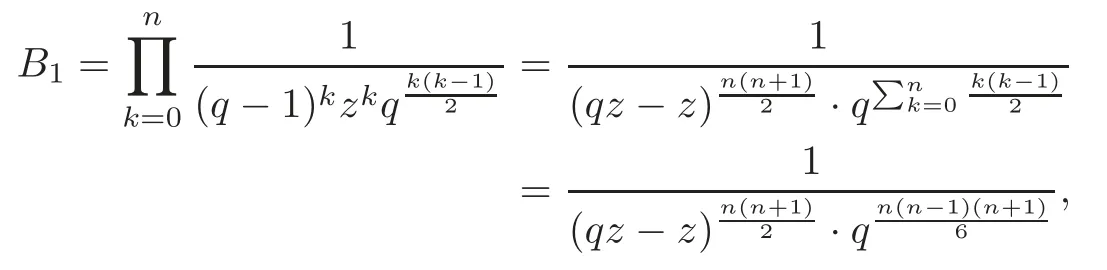
setB=we obtainCq(g0,···,gn)=CJ(g0,···,gn)·B.

For the classical Nevanlinna theory,we have the fact that entire functionsf0,···,fnare linearly dependent over C if and only if the WronskianW(f0,···,fn) vanishes identically.Letc∈C,and let P1cbe the field of periodcmeromorphic functions defined in C of hyper-order strictly less than one.In general,we know(see[13])that entire functionsf0,···,fnare linearly dependent over the field P1cif and only if the Casorati determinant ofC(f0,···,fn) vanishes identically.Here we introduce the analogue of these results for the case of Jackson difference operator.

Lemma 3.2Let the holomorphic curve g=[g0:···:gn]: C→Pnsatisfy σ(g)=0and q∈C{0,1}.Then CJ(g0,···,gn)≡0if and only if the entire functions g0,···,gnare linearly dependent over the fieldP0q.

ProofSuppose thatg0,···,gnare linearly dependent over P0q.Then there existA0,···,An∈P0qwhich are not all identically zero and satisfyA0g0+···+Angn=0.This clearly implies that

The determinant of the coefficient matrix corresponding to system (3.2) is the Jacksonq-Casoratian determinantCJ(g0,···,gn).We notice that (3.2) has a nontrivial solution,henceCJ(g0,···,gn)≡0.

On the other hand,we will continue to prove it by induction.Forn=1,we assume thatCJ(g0,g1)≡0,and consider

whereA0,A1are meromorphic functions.Furthermore,(3.3) is equivalent to

and we have

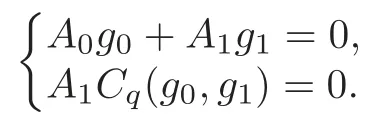
SinceCJ(g0,g1)=0,by Lemma 3.1 we getCq(g0,g1)=0,it follows thatandA1=−1 is a nontrivial solution of (3.3).Moreover,the usual order ofA0satisfiesσ(A0)=≤σ(g)=0 by (2.2).It is clear thatA1∈P0q.To complete the proof in the casen=1,we just need to show thatA0∈P0q.From (3.4),

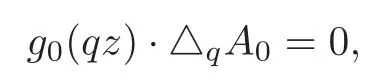
which implies that △qA0=0.ThenA0∈P0q.

For allj∈{1,···,k−1}andk≤n,supposeCJ(g0,···,gj)≡0,theng0,···,gjare linearly dependent over P0q.We will prove thatg0,···,gkare linearly dependent whenCJ(g0,···,gk)≡0 over P0q.We consider the linear system

whereA0,···,Akare meromorphic functions.According to (2.3) and (2.4) we have

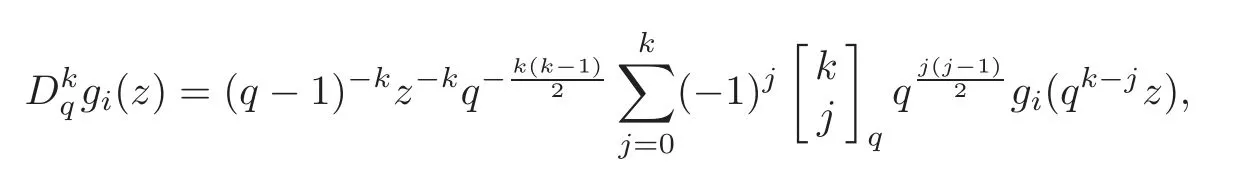
wherei=0,···,k.Therefore

implies

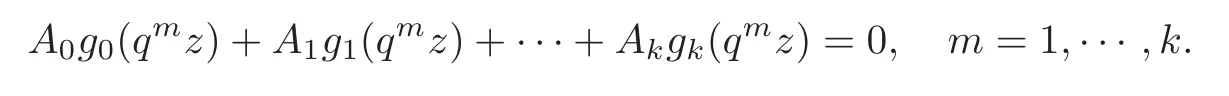
So the linear system (3.5) is equivalent to

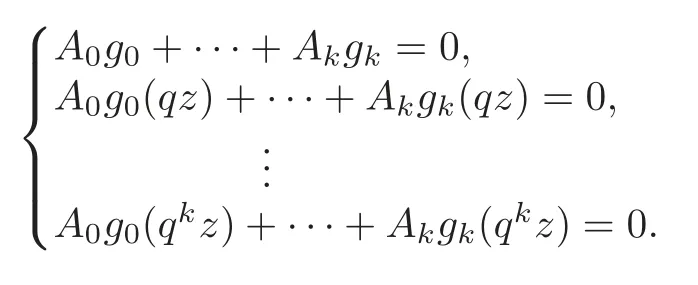
Then following the same method in[13,Lemma 3.2],we can getg0,···,gkare linearly dependent over P0q.

Lemma 3.3(see [2])Let f be a non-constant zero-order meromorphic function,and q∈C{0}.Then

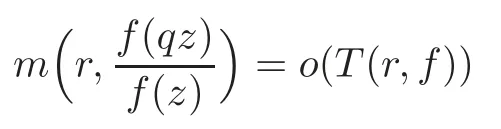
on a set of logarithmic density1.

Lemma 3.4(see [4])Let f be a nonconstant meromorphic function with zero order and q∈C{0}.Then

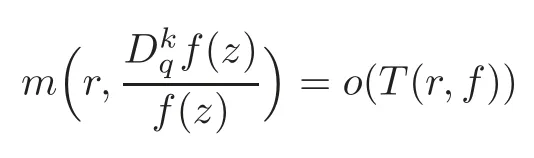
on a set of logarithmic density1.

Lemma 3.5(see [8])Let n≥1,z∈Cand let g0,···,gnbe linearly independent entire functions such thatmax{|g0(z)|,···,|gn(z)|}>0for each z∈C.If f0,···,fpare p+1linear combinations of the n+1functions g0,···,gn,where p >n,such that any n+1of the p+1functions f0,···,fpare linearly independent,then there exists a positive constant A that does not depend on z,such that

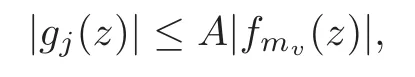
where0≤j≤n,0≤ν≤p−n and the integers m0,···,mpare chosen so that

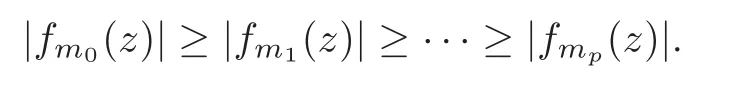
In particular,there exist at least p−n+1functions fjthat do not vanish at z.

Proof of Theorem 3.1We follow the reasoning behind the original Cartan’s second main theorem (see [11]) and the difference analogue of Cantan’s second main theorem (see [13]).Because the functionsg0,···,gnare linearly independent over P0q,by Lemma 3.2 we haveCJ(g0,···,gn)0 and the functionLgiven by (3.1) is well defined.The functionsg0,···,gnare also linearly independent over C (since C ⊂P0q),thus by Lemma 3.5 the auxiliary function

gives a finite real number for allz∈C.Let {a0,···,ap−n−1}⊂{0,···,p},and {b0,···,bn}={0,···,p}{a0,···,ap−n−1}.Similarly,forn+1 linearly independent functionsfb0,···,fbn,we getCJ(fb0,···,fbn)0 and

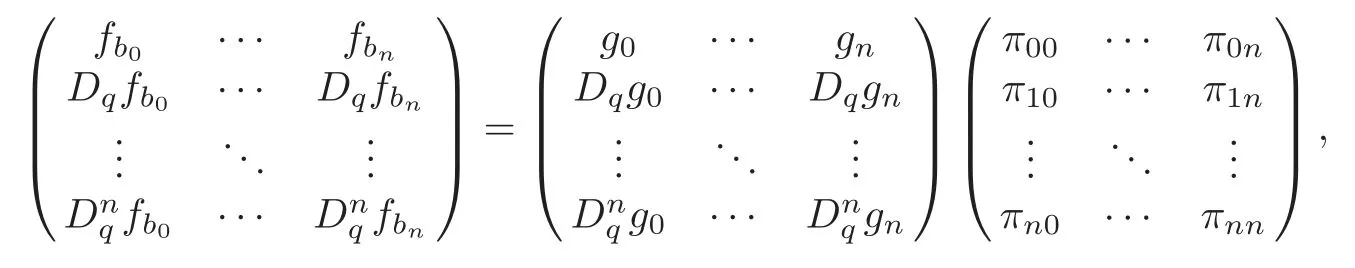
whereπjm∈C for allj,m=0,···,n.Therefore,

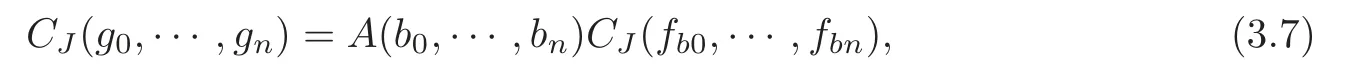
whereA(b0,···,bn)=:Ab∈C{0}. By Lemma 3.1 and (3.1),we have

where

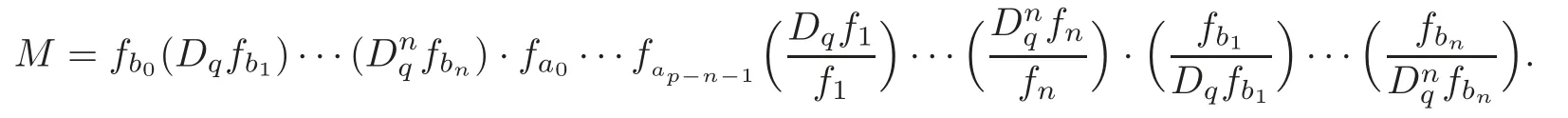
Therefore

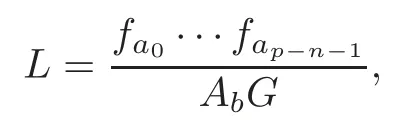
where

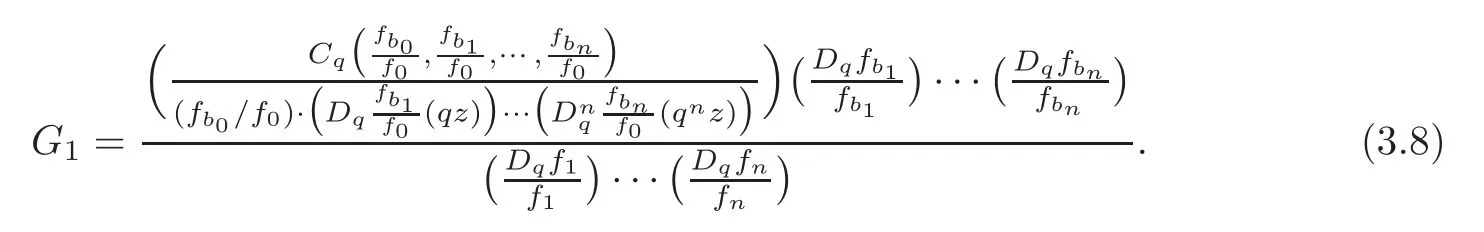
Set

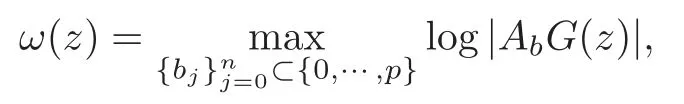
it follows that

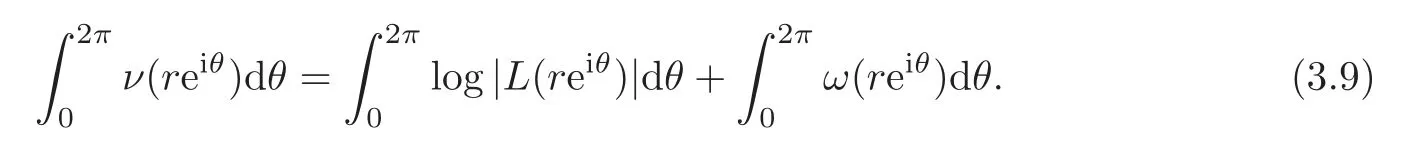
Suppose {c0,···,cp−n−1} is the set of indexes that make (3.6) have the maximum value for a specificz∈C.Then by Lemma 3.5,it is not difficult to see the inequality

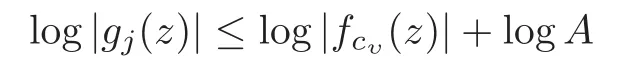
holds for all 0≤j≤nand 0≤υ≤p−n−1,and

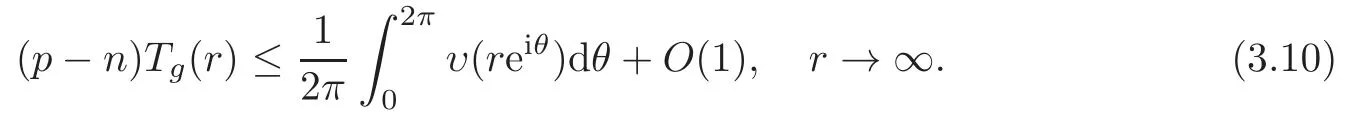
Since the functionG1in(3.8)consists purely of sums,products and quotients of fractions of the formwherel∈{1,···,n},j,k∈{0,···,p}.We deduce from Lemmas 3.3–3.4 that

asrapproaches infinity on a set of logarithmic density 1.It yields from (3.11) and (2.2) that

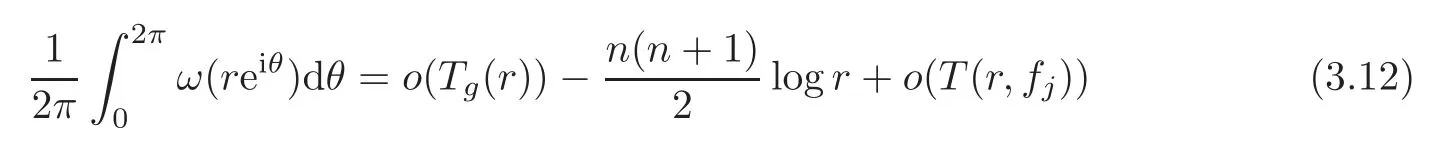
asrtends to infinity on a set of logarithmic density 1.

Finally,by Jensen’s formula

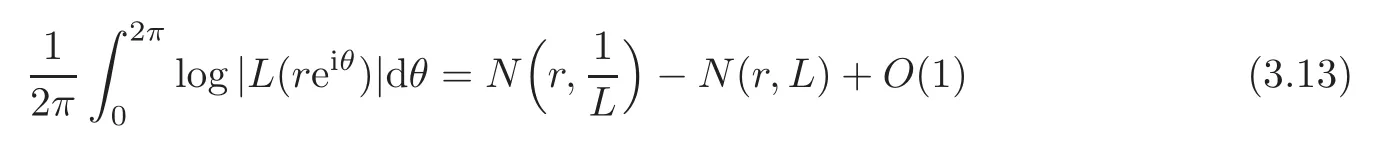
asr→∞.Combining (3.9),(3.10),(3.12) and (3.13),it yields out

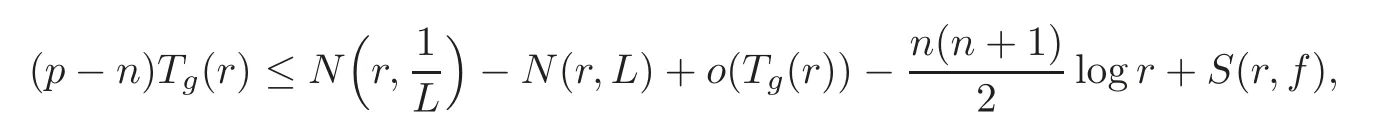
whereS(r,f)=o(T(r,fj)),j=0,···,p.

Furthermore,we obtain the following result about a truncated second main theorem of Jackson difference operator for holomorphic curve.

Theorem 3.2Let g0,···,gn(n≥1)be entire functions with no common zeros,linearly independent overP0q,and gn+1=g0+···+gn.If the holomorphic curve g=[g0:···:gn]:C→Pnsatisfies σ(g)=0,then

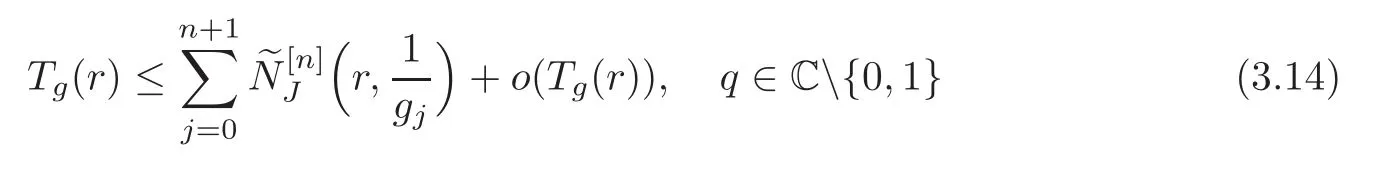
as r→∞on a set of logarithmic density1.

ProofWe define

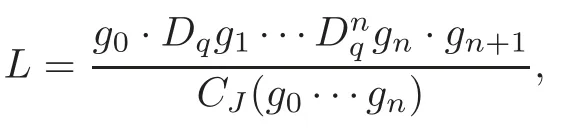
whereCJ(g0,···,gn) is the Jacksonq-Casoratian determinant ofg0,···,gn.Supposeωis a zero ofL,we assert that

Sincen≥1,g0,···,gnare linearly independent over P0qwith no common zeros,andgn+1=g0+···+gn.We havegn+1(z)≠0 for allz∈C.To illustrate that (3.15) is correct,we write

Note that the zeros ofLare the poles of some ofThe maximal order of poles among the first column in the determinant above is given by

It is worth noting that ord+ω(Djq(gp))≤ord+ω(gp)(j=2,···,n;p=1,···,n),thus the maximal order of poles among thejcolumn in the determinant above is given by

Hence for allz∈C,the inequality (3.15) holds and we get

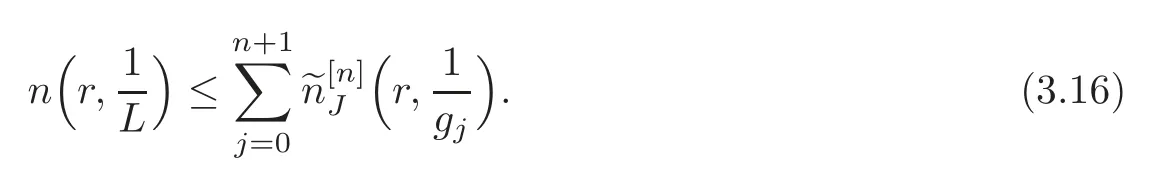
Then by applying Theorem 3.1 and integrating (3.16),we obtain (3.14).

4 Mason’s Theorem with a Jackson Difference Radical

Mason’s theorem is a counterpart of theabcconjecture in number theory.We state it here as follows.

Mason’s Theorem(see [14,19,24]) If relatively prime polynomialsa,bandc,not all identically zero,satisfy

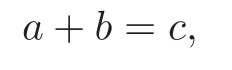
then degc≤deg rad(abc)−1,where the radical rad(abc)is the product of distinct linear factors ofabc.

In[14],we know that the Fermat’s last theorem for polynomials is an elementary application of Mason’s theorem.For any polynomialp(z)∈C[z],the usual radical radp(z) (see [3,14]) is defined by

where

Similarly,we define theq-difference radical radq(p) and the Jackson difference radical radJ(p)of the polynomialp(z).

Definition 4.1Let q∈C{0,1},we define the q-difference radical radq(p)and the Jackson difference radicalradJ(p)of the polynomial p(z)as

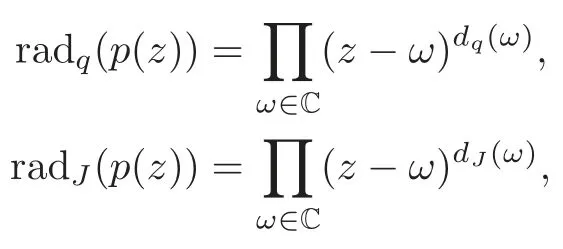
where

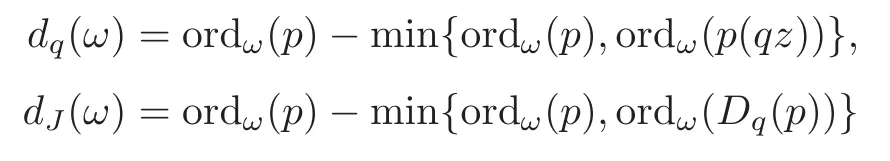
withordω(p)≥0being the order of zero of the polynomial p(z)at ω∈C.

Definition 4.2We denote(p)=deg radq(p)and(p)=deg radJ(p),more precisely,

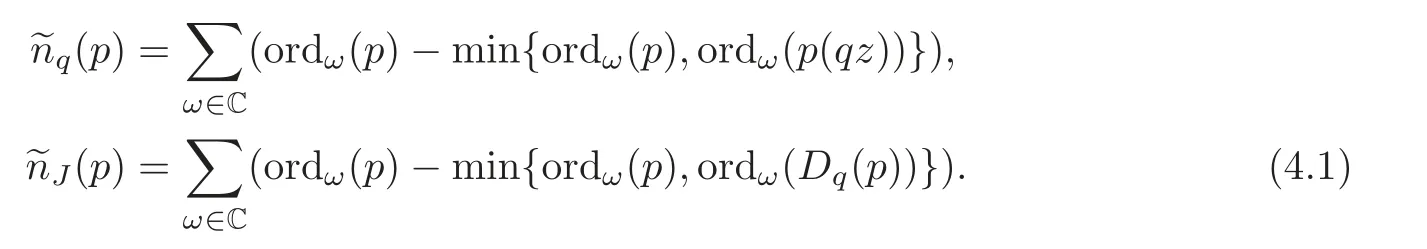
Remark 4.1In fact,we obtain the following properties for(p):

(3)

for anyp(z),h(z)∈C[z],where the equality holds exactly when bothp(z) andp(qz),p(z) andh(qz),h(z) andp(qz),as well ash(z) andh(qz) are relatively prime.

As we all know,for anyai(z)∈C[z],the differential operatorsatisfies

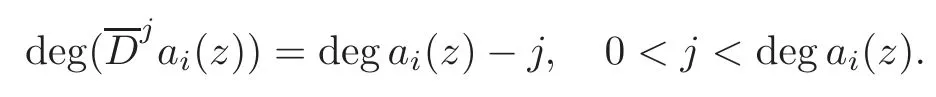
To better interpret the proof of Theorem 4.2,we need to introduce some notations.

Definition 4.3The corresponding q-difference radical and Jackson difference radical of truncation level m is defined by

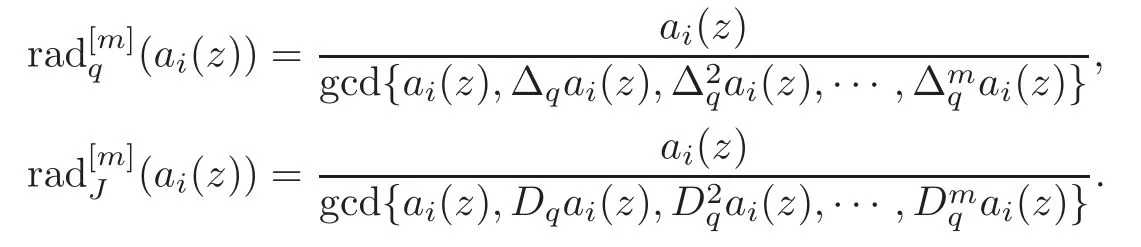
Remark 4.2When 0/∈{ai(z)−1(0)},we deduce that

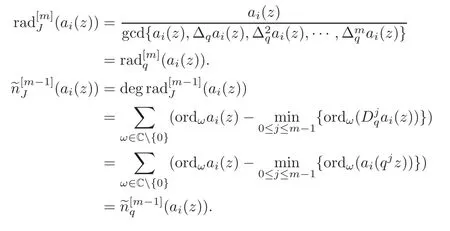
Here,we will use the Jackson difference radical radJ(p) to prove the Jackson difference analogue of Mason’s theorem.Furthermore,we extend the Jackson difference analogue of Mason’s theorem form+1 polynomials.We get the following theorems similarly as [14].

Theorem 4.1Let a1,a2,a3be relatively prime polynomials inC[z]such that

a1,a2,a3are not all constant and0/∈{ai−1(0)},i=1,2,3.Then

where q∈C{0,1}.

Theorem 4.2Let a1,···,am+1be pairwise relatively prime polynomials inC[z]such that

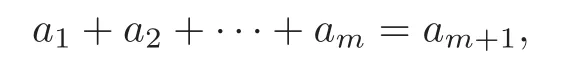
where a1,···,amare not all constant and linearly independent overC.In addition,0/∈(0),i=1,···,m+1.Then

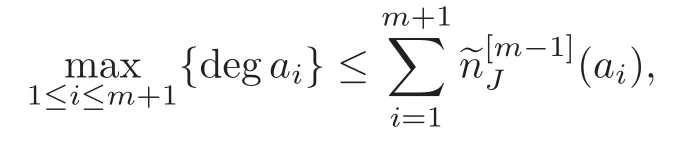
where we denote

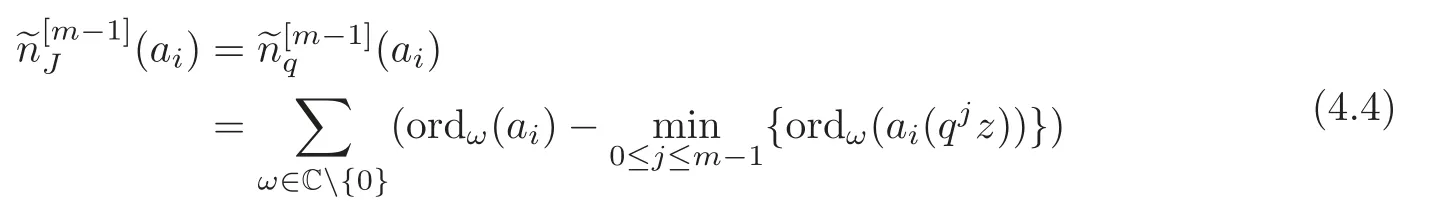
and q∈C{0,1}.

Lemma 4.1Suppose that p(z)0is a polynomial inC[z],q∈C{0,1}.Then

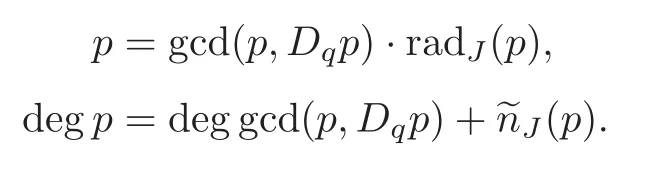
ProofLetαi0 be the roots ofp(z) with multiplicitiesairespectively,and not all ofaiequal to zero,wherei=1,2,···,m,that is

and thus

We will prove the lemma by distinguishing two cases:

Case 1If the origin is not the root ofp(z),we have

wherebi=min{ordαip(z),ordαip(qz)},i=1,2,···,m.

Since

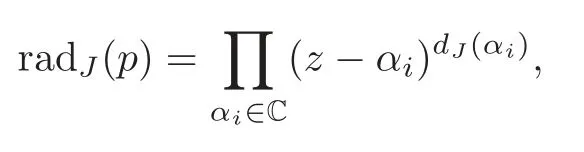
it leads to

hence

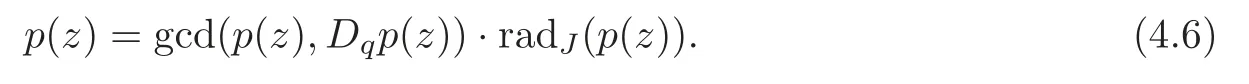
Case 2Let the origin be the root ofp(z) and the multiple bem,then

wherebi=min{ordαip(z),ordαip(qz)},i=1,2,···,m.

While

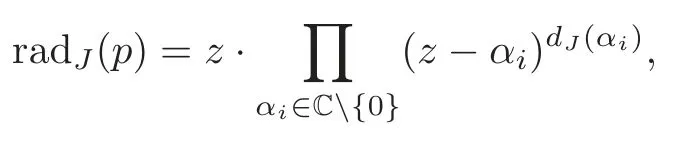
so combine with (4.5) in Case 2 we still have (4.6).

Therefore by Cases 1–2,it gives

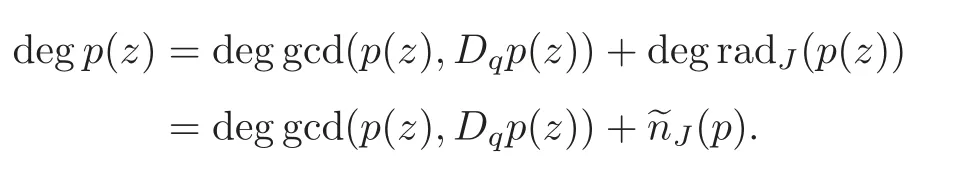
Proof of Theorem 4.1Without loss of generality,we may assume that

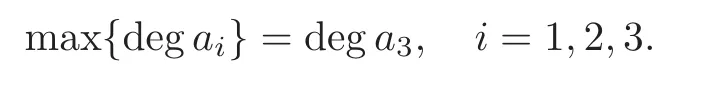
From (4.2) we see that

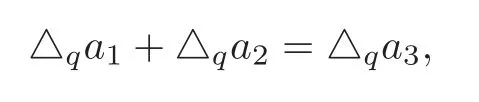
Clearly,

By subtracting (4.8) from (4.7),we have

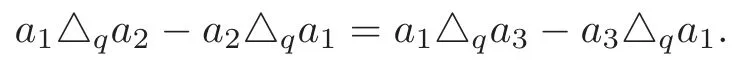
It is easy to see that gcd(ai,△qai) are factors ofa1△qa2−b△qa1.

Notice thata1,a2,a3are relatively prime,it means that gcd(ai,△qai) are relatively prime.Therefore,

is a factor ofa1△qa2−a2△qa1.By calculation,we get

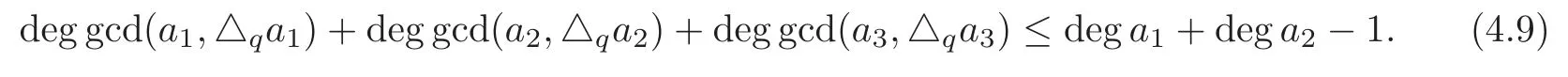
We claim thata1△qa2−a2△qa1≠0.Suppose for the contrary that

thena1△qa2=a2△qaanda1is a factor ofb△qa1.Sincea1anda2are relatively prime polynomials,we geta1is a factor of △qa1.This is only possible if △qa1=0.Similarly,it is easy to deduce △qa2=0 and △qa3=0.Thus,it contradicts the hypothesis of the theorem.Hence (4.9) is valid.

According to

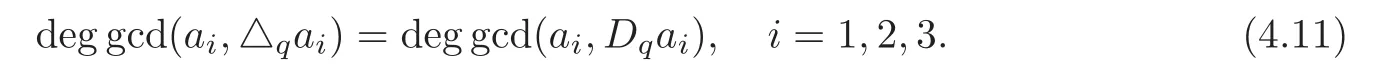
By adding dega3to both sides of (4.9) and reorganizing the term,we obtain

dega3≤dega1−deg gcd(a1,Dqa1)+dega2−deg gcd(a2,Dqa2)+dega3−deg gcd(a3,Dqa3)−1.

So (4.3) holds by Lemma 4.1.This finishes the proof of Theorem 4.1.

Example 4.1Setwhereα,β∈C{0},α≠βandα+β≠α(1+q).Clearly,a1,a2,a3are relatively prime polynomials in C[z]and satisfya1+a2=a3.Besides,none of the differences△qa1,△qa2,△qa3are identically zero.By calculation we get max{dega1,dega2,dega3}=2,The example shows that the assertion of Theorem 4.1 is sharp.

Example 4.2Supposeβ）. On account of thata1,a2,a3are relatively prime polynomials in C[z],we haveβ≠0.When 0 ∈a−1i (0),i=1,2,3,we get deg gcd(ai,△qai)=deg gcd(ai,Dqai)+1. Combining the inequality (4.9) yields

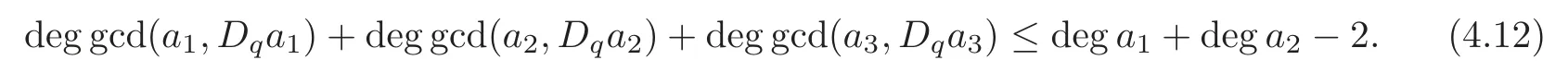
By adding dega3to both sides of (4.12) and reorganizing the term,we have

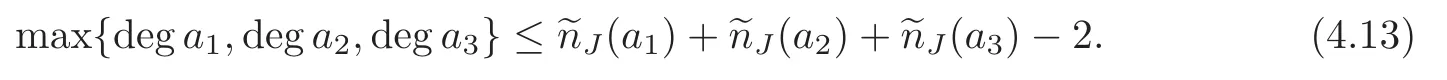
However,by calculation we get max{dega1,dega2,dega3}=2,this contradicts(4.13).So the example shows that the condition of 0/∈{ai−1(0)} (i=1,2,3) in Theorem 4.1 cannot be simply dropped.

Proof of Theorem 4.2Through the introduction of the second part,we know thatCq(z)0 is theq-Casorati determinant ofa1(z),···,am(z).Letz0≠0 be a zero of someai(z)with 1≤i≤m+1.Obviously,z=z0is also a zero ofCq(z)with multiplicity not smaller than

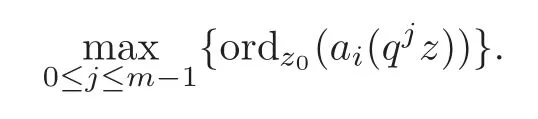
Sincea1,···,am+1are pairwise relatively prime polynomials,we get

is a factor ofCq(z),and there exists a polynomialp(z) ∈C[z]such thatCq(z)=p(z)q(z).Combining with (4.4),we deduce that the degree ofq(z) is not less than

On the other hand,the degree ofCq(z) is never beyond any sum of distinctmof the degai(z)(1≤i≤m+1).That is

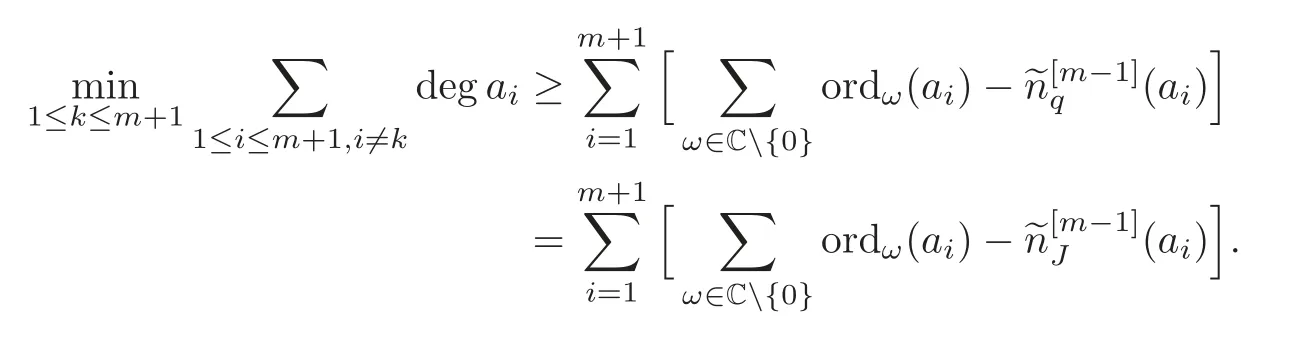
Hence

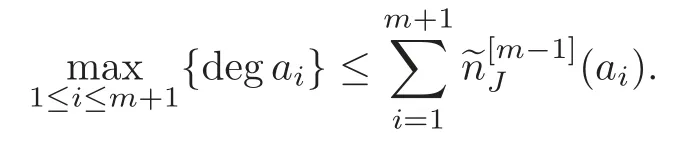
The following example shows that Theorem 4.2 is accurate whenm=3.

Example 4.3Take

andq∈C{0,1},α∈C{0}.Thusa1,a2,a3,a4satisfy the equationa1(z)+a2(z)+a3(z)=a4(z) and the condition of Theorem 4.2.This example gives

Remark 4.3In Theorem 4.2,we assume that the origin is not a root ofai,i=1,···,m+1.Otherwise,suppose that 0 ∈(0),we can get the relationship between(ai) and(ai).Denote by ord0(ai) the order of polynomialaiat the origin.Combining the definition ofDqaiand(ai),we easily verify that if ord0(ai)>m−1,

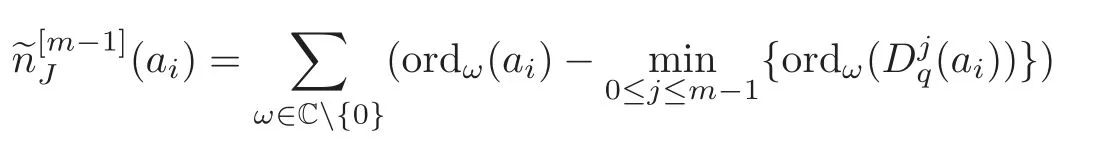
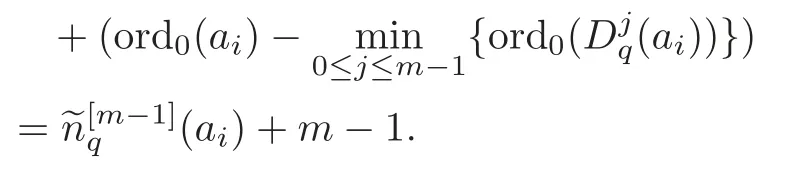
If ord0(ai)≤m−1,thenUnfortunately,this situation may not hold for Theorem 4.2.

Finally,we propose an interesting problem deserved to be further studied.

Problem 4.1Factorial polynomial is defined as

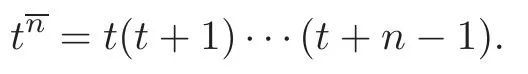
Ishizaki-Korhonen-Li-Tohge [14]introduce the notation for the factorial of a polynomialp(z)in C[z]as

where the shiftκ∈C{0}.

If we extend this notation for the factorial of a polynomialp(z) in C[z]as

whereq∈C{0,1}. What about the existence of polynomial solutions to a Jackson difference Fermat equations such as

AcknowledgementThe authors are very grateful to the referees for some valuable suggestions and comments.