软地层随钻测井仪器偏心情况下低频四极子源激发波场的数值分析∗

闫向宏 朱 琳 闫世鹏 方恒忠 杨喜峰

(1 中国石油大学(华东)理学院 青岛 266580)

(2 中国石油大学胜利学院教务处 东营 257061)

0 引言

声波测井是获取地层纵波速度、横波速度和孔隙度的重要手段[1]。电缆测井中采用偶极横波测井来测量低速地层的横波速度[2−3]。对于随钻声波测井(Logging while drilling,LWD)而言，因钻铤占据了井孔中的大部分空间，并且声波测量设备都固定在钻铤上，原有的偶极横波测井理论已不适用随钻过程中低速地层横波速度的测量[4−5]。为解决这个问题，国内外学者对随钻过程中低速地层横波速度的测量进行了理论探究，提出了采用低频随钻四极子波测量低速地层的横波速度[6−10]。考虑到随钻声波测井仪器用于斜井或者水平井测量时，随钻声波测量仪器的偏心会对井孔中波场特性产生影响。文献[11–12]利用有限差分法对含偏心点源随钻声波声波测井偶极子波场及随钻偏心单极子源波场进行了研究[13]；文献[14]给出了随钻单极子波场的解析解，并对高速地层、低速地层的波场的频散特性进行了深入讨论；文献[15]讨论了水平井和大斜度井中多极声波随钻测井的波场，并对低频四极子波源偏心角度与接收波形相位角之间的关系进行了分析。但上述文献对随钻低频四极子偏心声源激发波场频散特性及各模式波幅度随偏心距离的变化规律研究比较少，为此有必要对低频随钻四极子偏心声源激发波场的特性进行研究，有助于进一步丰富完善随钻四极子波场理论及地层横波速度测量技术。

1 低频随钻四极子声源激发波场的有限元模型

利用多物理场耦合有限元软件包Comsolmultiphysics 构建软地层井孔中低频随钻四极子源激发波场的有限元模型如图1所示。图1中T为声波发射换能器，它由4 个圆心角为90◦的圆柱面组成，发射单元分别记为(T+,T−)，其中T+两个单元、T−两个单元相对放置，并且T+两个单元与T−两个单元施加反向激励信号，R1～R6为接收换能器阵列，间距为0.1524 m，每组接收换能器Ri由4 个圆心角为90°的圆柱面组成接收单元，并按照一定的运算规则输出换能器Ri的测井接收波形。发射、接收换能器都安装在钻铤上，钻铤内半径r0=0.027 m，外半径r1=0.089 m，井孔半径r2=0.12 m，地层外半径0.5 m，地层外表面为吸收边界。在发射换能器T上加载余弦高斯激励脉冲信号，激励信号的主频为2000 Hz，其时域波形及归一化频谱如图2所示。

图1 圆形井孔四极子源波场计算的有限元模型示意图及井孔俯视图Fig.1 The profile view and vertical view of finite model

2 低频随钻四极子源在软地层井孔中激发波场的数值模拟

在有限元软件中按照图1所示建立数值计算模型，其中井孔介质的参数见表1。分别计算低频随钻四极子声源居中或者偏心时激发的声场，利用接收换能器阵列获取相应的测井波形，并利用时间慢度相关(Slowness time coherence,STC)法[16]和频散慢度分析(Dispersion slowness analysis,DSA)法[17−18]对测井波形进行处理，分析声场特性。

表1 井孔介质参数表Table 1 Parameters of borehole mediums

2.1 低频随钻四极子声源在井孔中激发波场的特性

圆形井孔中居中低频四极子声源激发波场的时域阵列接收波形如图3(a)所示，对时域接收阵列波形进行STC 法和DSA 法处理，得到如图3(b)所示的STC 图及图3(c)所示的频散曲线。从图3(a)中可以看出，当低频随钻四极子声源与井孔轴线完全重合时，发射单元或者接收单元相对于井孔均处于完全对称状态，低频随钻四极子声波测井的阵列波形具有比较清晰的到时起点，且只存在一种模式波。由STC图可得该模式波的慢度所对应的声波速度为1200 m/s。由文献[6,9–10]可知，随钻四极子声源低频时只激发地层模式的四极子波，且截止频率附近以地层横波速度传播。从图3(c)可知模式波具有频散特性，其频散曲线在截止频率(约2.5 kHz)处该模式波传播速度约为1200 m/s，与正演计算输入的地层横波速度(1200 m/s)基本相同，由此可知该模式波为地层四极子波。

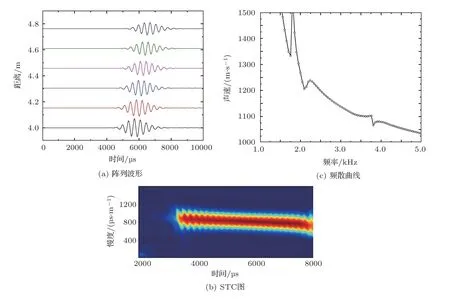
图3 圆形井孔四极子中心源随钻四极子声波测井阵列波形、STC 图和软地层四极子波频散曲线Fig.3 The full wave calculating result of LWD quadrupole array reception waveform,STC,and dispersion figure of quadrupole wave pattern for soft formation of the source in center of circle borehole using FEM method

2.2 低频随钻偏心四极子声源在井孔中激发波场的特性

为了表述及研究问题的方便，假设选取低频随钻四极子声源中心沿x轴方向偏离井孔轴线(对其他偏心方向可采用相同方法处理)位置分别为xoff=0.00 m、0.005 m、0.01 m、0.015 m 和0.02 m，分别计算圆形井孔中偏心四极子声源激发的声场，研究声源偏心位置对低频随钻四极子声波测井时域波形的幅度及波动模式的影响规律。

图4给出了低频随钻四极子声源在不同偏心位置时激发波场中同一接收器输出的随钻四极子声波阵列波形。从该阵列波形图中可以看出，随着四极子声源偏离中心，中心声源原来仅有的一个波包(对应地层四极子模式波)的前面出现了另外一个幅度很小的波包，由此可推断出在圆形井孔中四极子声源偏心时，可激发出两种波动模式。为此选择四极子声源偏心xoff=0.01 m 时的随钻四极子声波测井阵列波形进行STC 及DSA 处理，给出相应的低频随钻声波测井阵列波形、STC图及频散曲线图如图5所示。从STC图中也能明显看到存在两种不同速度的波动模式，其中幅度大的为地层四极子模式波，在其前方出现了一种速度约为1530 m/s 的波动模式(该波动模式记为W 模式波，文中下同)。由图5(c)可以看出，W 模式波传播速度随频率升高而增大，也是弱频散的，在激励源主频处其传播速度为1527 m/s，结合文献[10]中低频随钻多极子波的频散曲线可知，该W 模式波为钻铤弯曲波。由图4中波形可看出，随着低频随钻四极子声源偏心距离的增加，钻铤弯曲模式波和地层四极子模式波的幅度都增大了，并且钻铤弯曲模式波的出现使得地层模式波的到时起点变得不太清晰，其主要原因是由于组成发射换能器的4 个单元及组成接收换能器的4 个单元与井孔轴线间处于完全不对称状态，导致各个接收单元输出信号存在差异，从而使低频随钻四极子声波测井阵列波形中存在了两种波动模式，并且其波形幅度与偏心距离有关。图6为低频随钻四极子声源偏心位置与两种波动模式的幅度之间关系曲线，其中图6(b)利用井孔中居中声源时的地层四极子波幅度对偏心声源地层四极子模式波的幅度进行了归一化处理。钻铤弯曲模式波幅度随着偏心距离的增大呈现二次方规律增加，而地层四极子模式波的幅度随着偏心距离的增大呈现三次方规律增加，并且当偏心距离大约为井孔半径的15%时，地层四极子模式波幅度达到极大值。

图4 圆形井孔中声源偏心不同距离时同一位置的测井接收波形Fig.4 The reception waveform at same position for different eccentric distance in circle borehole

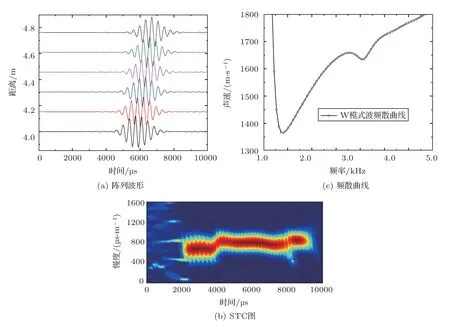
图5 圆形井孔中声源偏心0.01 m 时随钻四极子声波测井阵列波形、STC 图及W 模式波频散曲线Fig.5 The full wave calculating result of LWD quadrupole array reception waveform,STC figure,and W wave pattern dispersion figure for the source offcenter 0.01 m of circle borehole using FEM method

图6 声源偏心位置对圆形井孔中随钻四极子声波测井波形幅度影响曲线Fig.6 Amplitude curve vary with the eccentric position for the W wave pattern and the formation quadrupole wave pattern

3 结论

(1) 低频随钻四极子偏心声源在低速地层井孔中会激发两种波动模式，一种是传播速度与低速地层横波速度相当的地层模式波，另一种是传播速度高于井孔流体声速的模式波(W 模式波即钻铤弯曲模式波)；

(2) 在随钻四极子声波测井接收波形中，钻铤弯曲模式波幅度很低且位于四极子模式波的前方，因此会造成地层四极子模式波没有清晰的波至点，因此必须探索更有效的低速地层横波速度提取方法；

(3) 随着低频四极子偏心声源离开井孔中心距离的增大，钻铤弯曲模式波的幅度按照二次方规律增大，而地层四极子模式波的幅度按照三次方规律增加，当偏心距离大约是井孔半径的15%时，地层四极子波幅度达到极大值。