基于Python编程模拟四极杆质谱中离子的运动

张 硕，方开洪，王 强，陈 亮，杨坤杰

(1.兰州大学 核科学与技术学院，甘肃 兰州 730000；2.烟台大学 核装备与核工程学院，山东 烟台 264005)

四极杆是一种仅利用电场，无需磁场的质谱分析方法，其具有结构简单、体积小的优点；且四极杆质谱仅要求离子能量低于一定限值，不需要离子能量一致；通过调节四极杆的直流和交流电压，一台质谱仪可实现不同的分辨率、灵敏度，以满足不同情况下的分析要求。基于以上优点，四极杆自诞生后迅速发展[1-3]，目前已被广泛应用于物理学、分析化学、环境科学、食品科学等众多领域[4-6]。

在大学物理实验中，四极杆质谱是一种重要的质谱教学仪器。该实验可令学生充分理解质谱进行元素分离的原理，熟悉常用的质谱仪器，为未来的科研和工作打下良好的基础。然而离子在四极杆中的运动过程并不能直观观察，且离子运动受到众多因素的影响，这对于学生理解四极杆的原理造成一定的难度。此外，由于实验教学条件的限制，很多高校并没有开设四极杆质谱的相关实验，对于学生熟悉常用的质谱方法造成一定的困难。利用计算机模拟仿真离子在四极杆质谱中的运动过程可摆脱对实验教学条件的限制，同时能够将离子在四极杆中的运动过程直观的展现出来，对于学生深入、直观地理解四极杆质谱的原理以及元素的分离过程具有重要的补充作用。

本工作基于Python语言编写一套模拟离子在四极电场中运动轨迹的数值程序，并将离子的运动轨迹以图像的形式展现出来，让学生对于四极杆质中离子的运动过程有一个直观的认识。本工作开发的模拟程序可以对四级杆的结构参数、外加电压参数、离子种类参数以及离子进入四级杆的初始条件等参数进行分别调节(部分参数为真实的实验中难以调节的参数)，并直观地给出相应条件下离子的运动过程。

1 四极杆质谱的基本原理

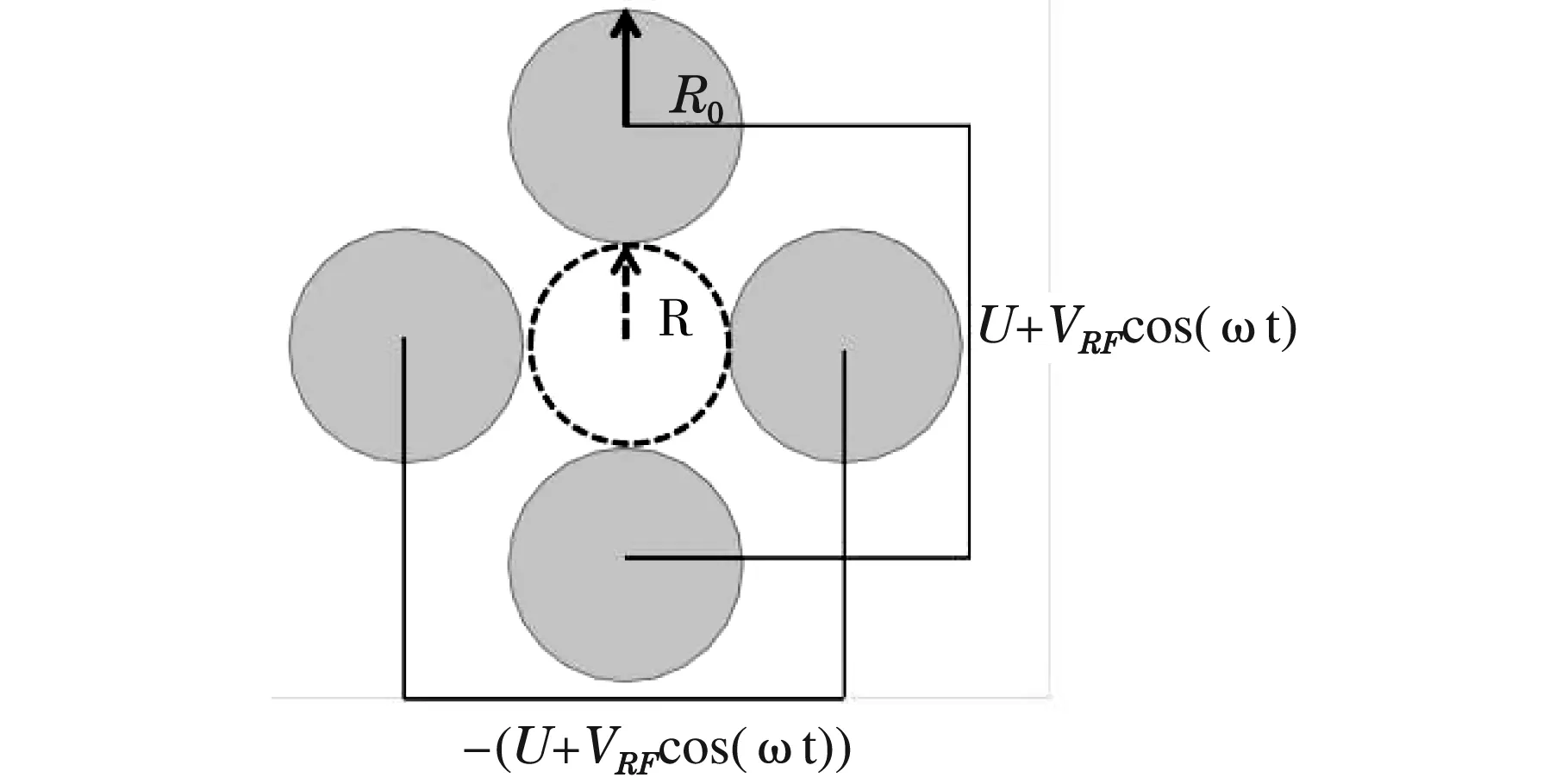
四极杆质谱一般采用四根半径相等的圆柱形极杆构建四极电场，其结构示意图如图1(a)所示，两两相对的电极杆为一组，分别在两组杆上施加大小相等，极性相反的直流C和频率为ω的射频电压VRF，即Φ=±(U+VRFcos(ωt))，以此构建四极电场。在四极杆质谱中，我们称四根极杆的半径为杆半径R，四根杆中间的相切圆的半径称为场半径R0，其三维图如图1b图所示。

a

研究已经证实，在杆半径R为场半径R0的1.130～1.148倍时，四根极杆构成电场最接近“理想”的四极电场[7,8]，误差在1%左右，目前大部分四极杆质谱仪器在制造过程中遵循该原则。在“理想”的四极电场中，沿着杆的Z方向上电势相等，四根杆的横截面上，任意一点(x,y)的电势可以写作为[9]：

(1)

四极杆内任意一点r(x,y,z)的电场为电势的梯度，可写作为E(Ex,Ey,Ez)：

(2)

在已知离子的电荷量和质量的情况下，可根据上述电场得到离子在四极杆中的运动方程：

(3)

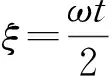
(4)

定义：

(5)

将定义的au和qu代入方程组(4)，可将离子在X和Y方向的运动统一为：

(6)

其中，u代表x或y。该方程称为Mathieu方程，方程解即为离子在四极杆中的运动轨迹。

Mathieu方程在数学中已经得到完整的解析解，通过对该解析解的分析可以得到离子在四极杆运动中稳定运动对应的约化参量au，qu值，这些值在构成了四极杆的稳定区。四极杆一般通过调节直流电压U和交流电压VRF，使选定的荷质比的离子落在四极杆的稳定区，其他荷质比的离子落在稳定区外。落在稳定区的离子在合适的初始条件下通过四极杆；落在稳定区外的离子将在运动过程中与杆发生碰撞并被杆吸收，因此稳定区外的离子将不能通过四极杆。根据离子能否通过四极杆，四极杆质谱实现了对不同荷质比离子的分离。

2 模拟方法介绍

为了直观模拟离子在四极杆中的运动，我们基于Python语言编写了一套模拟离子在四极电场中运动的数值模拟程序。

程序首先利用有限差分法计算了在给定四极杆结构参数(杆半径为R，场半径为R0，四极杆的长度为L)和电压参数下(直流电压U，射频电压VRF)空间内离散点的电场分布。带有电荷量为q的离子进入四极杆的初始位置为r0(x0,y0,z0)，初始速度为v0(vx,vy,vz)，初始时刻为t0。当离子进入四极杆后，我们根据离子位置和进入时刻，利用已知离散点电场插值计算离子在t0时刻和r0位置的电场，进而计算离子的受力和加速度a0，同时假定离子进入四级杆前的加速度a-1与a0相等，然后根据Beeman方法[10]计算离子在t0+Δt时刻的位置r1(x1,y1,z1)和离子在该位置的加速度a1，进而计算离子在该位置的速度v1，然后通过迭代计算r2，v2，r3，v3…，最终通过不断迭代得到离子在四极杆中的运动轨迹。其中Beeman方法的计算公式如式(7)所示。

(7)

当离子位置大于四极杆的场半径或由四极杆的末端射出后，离子轨迹模拟结束。得到离子轨迹后，程序可以以图像或动画的形式将离子的运动过程展现出来。

影响离子在四极杆中运动方程的因素有很多，包括直流电压U，射频电压VRF，射频频率ω，离子的荷质比q/m，以及离子的场半径R0，本工作模拟了不同参数下离子的运动轨迹。

由于离子在理想四极电场中的运动方程最终可以化简为Mathieu方程，因此上述参量可通过(5)式简化为两个参量au和qu，即在相同au和qu条件下，离子的运动方程是相同的。本工作采用蒙特卡罗模拟方法，随机选取了20 000组不同的(au,qu)值，其中au的选取范围为[0,0.35]，qu的选取范围为[0,1.0]。在每组选定的(au,qu)条件下，基于本工作编写的Python程序模拟离子在四极杆中的运动轨迹，根据离子能否稳定在四级电场中运动构建了四极杆质谱的第一稳定区。

离子进入四极杆时的初始条件也会影响其运动轨迹，为了在教学过程中直观的展示初始条件对离子运动轨迹的影响，本工作还模拟了不同初始条件下离子的运动轨迹。

3 结果及讨论

3.1 离子运动轨迹的模拟

本工作构建的模拟程序可对四极杆的直流电压U，射频电压VRF，射频频率ω，离子的荷质比q/m，以及离子的场半径R0等参数进行独立调节。此处，为了展示模拟结果，我们给出了在部分参数下离子在四极杆中的运动轨迹，其中图2为可稳定通过四极杆的离子在其中的运动轨迹，其参数见表1所示，同时表1中给出了不同参数下对应的au和qu值。图2中红色虚线代表离子在X轴方向的运动轨迹，蓝色虚线代表离子在Y轴方向的运动轨迹。从图中可以看出，对于可通过四极杆的离子，离子在四极杆内出现周期性运动，其运动被“束缚”在四极电场之中。图2仅给出了离子通过四极杆的两个示例，不同条件下离子通过四极杆的轨迹可能有较大差异。图3是离子不能通过四极杆的两种运动轨迹图，其对应的参数以及au、qu值见表1。从图3(a)中可以看出，离子在Y轴方向的运动呈“发散”状态，随着离子在四极杆中的前进，离子由于与Y轴方向的杆碰撞而被杆吸收；而对于图3(b)，离子在运动过程中由于与X轴方向的杆碰撞而停止运动。图2和图3所展示的离子运动轨迹模拟均在相同的初始条件下开展的，离子在XY平面内坐标为(1 mm，1 mm)处以沿Z轴4 600 m/s的速度进入四极杆，进入四极杆的时刻为0时刻。

a

a

通过对不同参数条件下的离子运动的模拟，我们发现只要具有相同au、qu值以及相同初始条件的离子在四极杆中的运动轨迹几乎完全一致。根据四极杆的原理，离子的运动轨迹可最终简化为Mathieu方程，该方程的解同样仅与au、qu以及离子运动的初始条件有关。因此本工作模拟结果符合四极杆的基本原理。

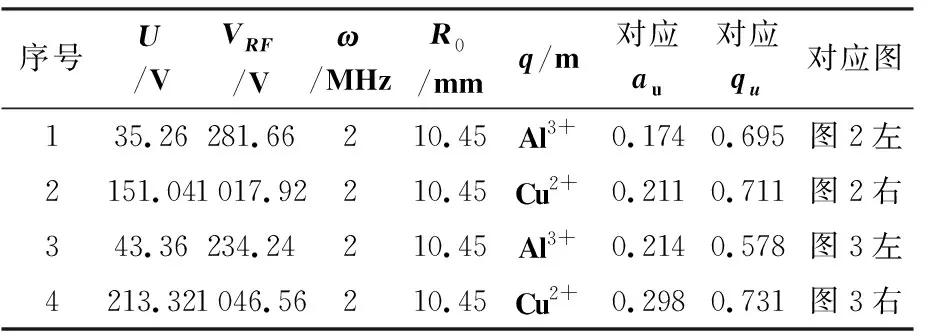
表1 离子轨迹模拟参数表

3.2 四极杆第一稳定区的模拟

从图2可以看出，可通过四极杆的离子的运动轨迹必须是“稳定”的，即运动轨迹在X轴和Y轴均不发散。稳定是离子通过四极杆的重要条件，Mathieu方程的数学解析解可以给出离子稳定运动对应的au、qu值域，图4中的红色虚线为Mathieu方程给出的第一稳定区边界。

本工作模拟了20 000组不同(au,qu)值下在临近四极杆中心位置入射时离子的运动轨迹，根据模拟结果我们将离子的运动分为两类：一类为离子运动轨迹为稳定的，即离子在四极杆运动过程中，其最大振动幅度为有限值；另一类为非稳定运动，即离子的振动幅度趋向于发散。模拟结果如图4所示，图中蓝色点代表在对应的au和qu值下离子运动轨迹为发散的，绿色点代表在相应的au和qu值下离子的运动轨迹为稳定的，从图中结果可以看出本工作的模拟结果与Mathieu方程给出的稳定区的边界近乎完全一致。

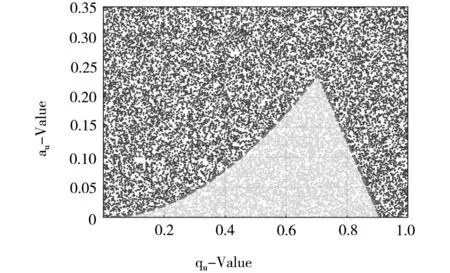
图4 不能通过四极杆的离子在质谱中的运动轨迹

3.3 不同初始条件对运动轨迹的影响

稳定是离子通过四极杆的必要条件，然而离子的运动轨迹同样会受到离子进入四极杆时初始条件的影响。为了研究初始条件对离子运动轨迹的影响，我们在离子稳定运动的au和qu值条件下，改变离子进入四极杆的初始位置、初始速度以及初始时刻，并对离子的运动轨迹进行了模拟。为了直观观察初始条件是否对离子运动的稳定性产生影响，在模拟中当离子的运动轨迹超出四极杆的场半径R0后，我们未停止离子运动轨迹的模拟，并假定其依旧在式(2)给出的理想四极电场中继续运动。

图5给出了在au=0.2，qu=0.7条件下，离子分别从XY平面的(1.102mm,3.90mm)(a)和(9.31mm,3.68mm)(b)处在0时刻以沿杆方向4 600m/s的速度进入四极杆后的运动轨迹。四极杆的场半径为10.45mm，图中以黑色实线标识。从图4中看出au=0.2，qu=0.7对应了离子在四极杆中稳定运动区域。从图5(a)中可以看出，当离子由XY平面内坐标为(1.102mm,3.9mm)处进入四极杆时，该离子可以通过四极杆。对于(b)中从坐标为(9.31mm,3.68mm)处进入四极杆的离子，尽管其运动轨迹仍然是稳定的，但是在真实情况下，由于其在X方向的振动幅度超过四极杆的场半径，该离子将不能通过四极杆。

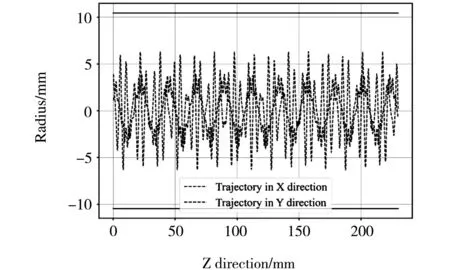
a 在au=0.2，qu=0.7条件下，离子分别从XY平面的(1.10 mm,3.90 mm)

当离子在稳定区条件下，如果不考虑四极杆的边界，由不同位置入射的离子，其运动都是稳定的。然而，靠近离子中心位置入射的离子在运动中其振动幅度较小，远离中心位置入射时，其振动幅度将逐渐增大，当离子振动的幅度超过四极杆的场半径后，离子将不能稳定通过四极杆。

4 总结及展望

由于四极杆中影响离子运动的因素众多，因此四极杆质谱元素分离的原理和特点是学生理解的难点之一。本工作基于Python语言编写了一套模拟离子在四极杆中运动轨迹的数值程序。该程序可直观地展示离子在四极杆中的运动过程。在实验教学过程中，学生可通过调节四极杆的结构参数、电压参数以及初始条件等参数对离子的运动轨迹进行模拟，通过观察不同参数下的离子运动轨迹可加深学生对四极杆原理和分离特点的理解。此外，本工作开发的程序为在高校开展四极杆质谱模拟仿真实验奠定了基础，可解决高校四极杆质谱实验的教学条件的限制。