抽象矩阵的可逆性探讨
2022-07-06薛维顺李秀兰
薛维顺,李秀兰
(1.山西晋中理工学院,山西晋中 030600;2.山西大同大学数学与统计学院,山西大同 037009)
关键字:抽象矩阵;可逆;特征值;特征多项式
矩阵的逆是高等代数和线性代数中的一个重要概念[1-2]。抽象矩阵的运算一直是广大学者关注的一个重点[3-7]。而抽象矩阵的逆矩阵求法是教学中的难点问题。通过对抽象实矩阵可逆性的探讨,总结出一些求抽象矩阵逆矩阵的方法。有助于教师的教学和学生的学习。
1 定义法
设A为n阶方阵,若存在n阶方阵B,使得AB=BA=E成立,则称矩阵A可逆,矩阵B是A的逆矩阵,记作A-1=B。
抽象矩阵的逆矩阵求法,对逆矩阵的灵活应用有较高的要求。特别对学生而言,这类题目相对较难,较难入手。
例1已知A,B,A+B均为n阶可逆方阵,证明A-1+B-1也可逆。

证明由于因此A-1+B-1可逆。
上述的证明利用了(AB)C=A(BC)的矩阵性质,并利用逆矩阵的定义进行了证明。在实际解题中可将结论作为一般的结果进行应用,来解决这一类逆矩阵的求解。
2 利用可逆矩阵的性质
在抽象矩阵的逆矩阵求解过程中经常会利用可逆矩阵的性质来进行运算,经常用到的公式为

例2A为n阶可逆方阵,且 |A|=λ1。证 明(λ2A)-1-λ3A*也可逆,其中λ2≠0,
证明因为A为n阶可逆方阵,所以AA*=|A|E。等号两端同时左乘A-1得,A*=|A|A-1=λ1A-1。
由此可得

这类逆矩阵的求解经常会结合行列式的性质|kA|=kn|A|来考查。在运算过程当中一定不能将|kA|与k|A|混淆。
3 利用“凑因式”
这种方法相对简单,处理的核心思想就是“凑”。将要求解的逆矩阵作为“核心”来凑出题设所给的条件,从而求解出抽象矩阵的逆矩阵。
例3设B为n阶方阵,满 足B=B2。若A=B+E,求当k≠1,2 时,A-kE可逆,并确定AkE的逆矩阵。
解由B=B2可得,

要使A-kE可逆,则必须有(k2-3k+2)E≠O,即k2-3k+2≠0,
所以,当k≠1,2时,A-kE可逆。
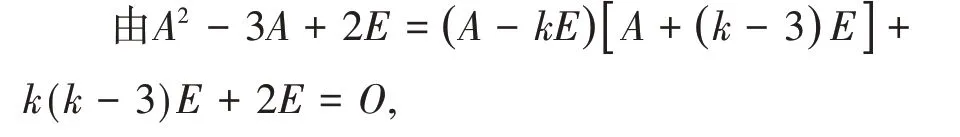
可得
(A-kE)[A+(k-3)E]=-(k2-3k+2)E,同时也确定了A-kE的逆矩阵为
在上述的证明过程中主要将A-kE看作主体,通过拼凑来实现题设所给的主要条件,即A2-3A。事实上,可以得到更一般的这类抽象矩阵的逆矩阵判定。能快速的判定这类矩阵的逆矩阵是否存在。在逆矩阵存在的前提下,再通过上述的方法来求逆矩阵。
例4设A为n阶方阵,满足A2+k1A+k2E=O,则有下列结论成立:
(1)若-4k2<0,则A-kE都可逆,对任意的k都成立;
(2)若-4k2=0,则A-kE都可逆,对任意的都成立;
(3)若-4k2>0,则A-kE都可逆,对任意的都成立。
证明
A2+k1A+k2E=(A-kE)[A+(k+k1)E]+k(k+k1)E+k2E=(A-kE)[A+(k+k1)E]+()k2+k1k+k2E,要使A-kE可逆,只需满足k2+k1k+k2≠0即可。
当-4k2<0时,k2+k1k+k2≠0恒成立;
当-4k2=0 时,只 要就能满足k2+k1k+k2≠0成立;
当-4k2>0时,只要就能满足k2+k1k+k2≠0成立。
在上述的证明方法中主要利用了一元二次方程的求解公式。这个方法虽然简单,但是在求解此类抽象矩阵的逆矩阵过程中却是非常有效的。此结论也可以作为这类抽象矩阵逆矩阵求解的一般判定方法来进行应用。
4 利用分块矩阵的运算
例5A,B为n阶方阵,若A+B与A-B可逆,证明可逆。
证明解法1:
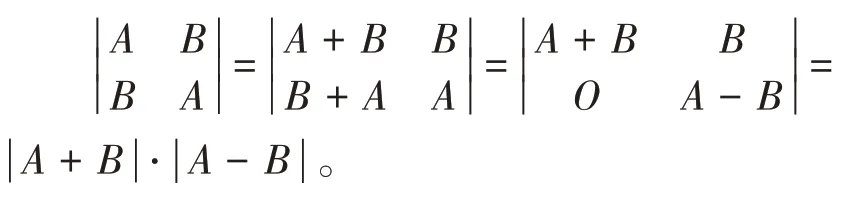
由A+B与A-B可逆,可得可逆。
解法2:

由⑤,⑥可知C1,C3是存在的;类似地可以验证C2,C4也是存在的。证毕。
在利用分块矩阵运算过程中一定要注意矩阵的左乘和右乘是不一样的,一般情况下AB≠BA。在计算过程中,当遇到,其中A,C分别为r阶和n阶方阵时,经常利用拉普拉斯定理求D的行列式来判定矩阵是否可逆,即 |D|=|A||C|。
5 利用矩阵的特征值
若矩阵A的特征值为λ1,λ2,…,λn,则 |A|=λ1λ2…λn[2];当A的特征值全不等于零时,矩阵A是可逆的。f(x)=xm+a1xm-1+…+am-1x+am是多项式,f(λi)(i=1,2,…,n)是f(A)的特征值。经常利用上述矩阵多项式的特征值来确定矩阵是否可逆。
例6A是n阶可逆方阵,是A的特征值,其中i1+i2+…+is=n。证明矩阵f(A)=Am+a1Am-1+…+am-1A+amE可逆的充分必要条件是λ1,λ2,…,λs不是多项式f(x)=xm+a1xm-1+…+am-1x+am的根。
证明因为A是n阶可逆方阵,故λi≠0(i=1,2,…,s)是矩阵A的特征值,则
f(λi)=+…+am-1λi+am(i=1,2,…,s) 是f(A)=Am+a1Am-1+…+am-1A+amE的特征值。要满足f(λi)≠0(i=1,2,…,s),只要λ1,λ2,…,λs不是多项式f(x)=xm+a1xm-1+…+am-1x+am的根即可。反之亦然。证毕。
6 结语
判定抽象矩阵是否可逆比判定具体矩阵可逆要复杂的多,而且办法也少。判定这类矩阵可逆的题目相对较难,对学生综合掌握知识的要求较高。在求抽象矩阵逆矩阵的过程中,同学们要善于思考并对遇到的问题进行归类,从而达到事半功倍的效果。
