二元指数型整函数的Carlson定理

陈 佳，康淑瑰

（山西大同大学数学与统计学院,山西大同 037009）

指数型整函数是纯数学理论中的一个主要课题，它在带有限函数的逼近问题中具有重要作用[1-4]。单变量的指数型整函数的Carlson 定理被广泛应用在函数的逼近问题中[5-7]，它表明如果指数型小于π 的整函数在所有整数点处的函数值为零，那么该函数恒为零[8-12]。单变量指数型整函数的Carlson 定理可以推广到高阶导数的情形:如果在复数域上的指数型小于kπ(k∈ℕ+)的整函数在所有整数点处的函数值及直到k-1 阶导数值都为零，那么该函数恒为零[8]。1978 年Gervais 和Rahman将单变量Carlson 定理做了如下的扩展：

定理A设f(z)，z∈ℂ 为指数型整函数。如果对所有n∈ℤ，都有f(n)=0，那么存在指数型整函数φ(z)，使得f(z)=φ(z)sin(πz)[13]。

定理B设f(z)，z∈ℂ 为指数型σ＜2π 整函数。如果对所有n∈ℤ，都有f(n)=f″(n)=0，那么存在常数A，使得f(z)=Asin(πz)[13]。

如果单变量指数型整函数f(z)，z∈ℂ 在整数点处具有高阶导数，那么f(z)的Carlson 定理有如下形式:

定理C设f(z)，z∈ℂ 为指数型整函数。如果对任意n∈ℤ，都有

f(n)=f′(n)=…=f(k-1)(n)=0，k∈ℕ+，那么存在指数型整函数φ(z)，使得

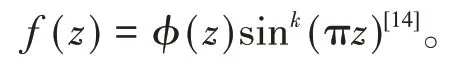
定理D设f(z)，z∈ℂ 为指数型kπ(k∈ℕ+)整函数且对任意n∈ℤ，都有f(n)=f′(n)=…=f(k-1)(n)=0。如果f(z)在ℝ 上有界，那么存在常数A，使得f(z)=Asink(πz)。

特别地，如果f(z) ∈Lp(ℝ)，1 ≤p＜∞，那么f(z) ≡0[14]。

定理A和定理C表明:如果复数域上的单变量指数型整函数f(z)在所有整数点处的函数值以及直到k-1(k∈ℕ+)阶导数值都为零，那么该函数f(z)等于sink(πz)与一个指数型整函数的乘积。定理B和定理D表明：如果复数域上的单变量指数型整函数f(z)在ℝ 上有界且在所有整数点处的函数值及直到k-1(k∈ℕ+)阶导数值都为零，那么f(z)可以由三角函数sink(πz)完全确定。

与一元情形类似，多元指数型整函数的Carlson定理在多元函数的逼近问题中也具有十分重要的作用。用多元复分析的方法研究二元指数型整函数的Carlson定理。

1 二元函数的Carlson定理

主要研究复数域上的二元指数型整函数的Carlson 定理。给出二元指数型整函数的定义和主要结论。

定理1设δ=(δ1,δ2)∈。称函数f(z1,z2)，(z1,z2)∈ℂ2为二维复数域上的指数型δ整函数，如果存在常数A＞ 0，使得对任意ε＞ 0，都有

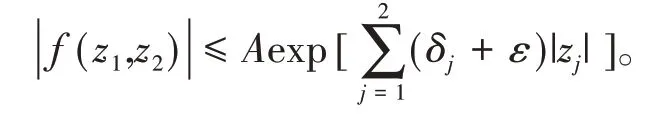
给出如下记号：

Eδ(ℝ2)表示限制在ℝ2上的指数型δ 整函数的全体。Bδ,p(ℝ2):=Eδ(ℝ2)⋂Lp(ℝ2)。二元函数f(z1,z2)，(z1,z2)∈ℂ2的整数r阶偏导数

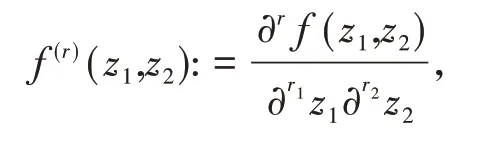
其中r=r1+r2，r1,r2∈ℕ。特别地，记一阶、二阶、三阶偏导数分别为f′(z1,z2)、f″(z1,z2)、f‴(z1,z2)[15]。

定理2设f(z1,z2)，(z1,z2)∈ℂ2为指数型整函数，且对任意(k1,k2)∈ℤ2，都有

f(k1,k2)=0,f′(k1,k2)=0,f″(k1,k2)=0,f‴(k1,k2)=0。则存在指数型整函数φ(z1,z2)，使得f(z1,z2)=φ(z1,z2)sin4(πz1+πz2)。

定理3设f(z1,z2)，zj=xj+iyj，xj,yj∈ℝ，j=1,2为指数型σ=(4π,4π)整函数，且对任意(k1,k2)∈ℤ2，都有f(k1,k2)=0,f′(k1,k2)=0,f″(k1,k2)=0,f‴(k1,k2)=0。

(1)若f(x1,x2)∈Bσ,∞(ℝ2)，则存在常数C，使得f(z1,z2)=Csin4(πz1+πz2)；

(2)若f(x1,x2)∈Bσ,p(ℝ2)，1 ≤p＜∞，则f(z1,z2)≡0。

2 定理的证明

用多元复分析的方法证明文中的定理，首先给出如下引理。

引理1设g(z1,z2)，zj=xj+iyj，xj,yj∈ℝ，j=1,2为指数型δ=(δ1,δ2)∈ℝ2+整函数[4]。

(1)若g(x1,x2)∈Bδ,∞(ℝ2),1 ≤p＜∞，则

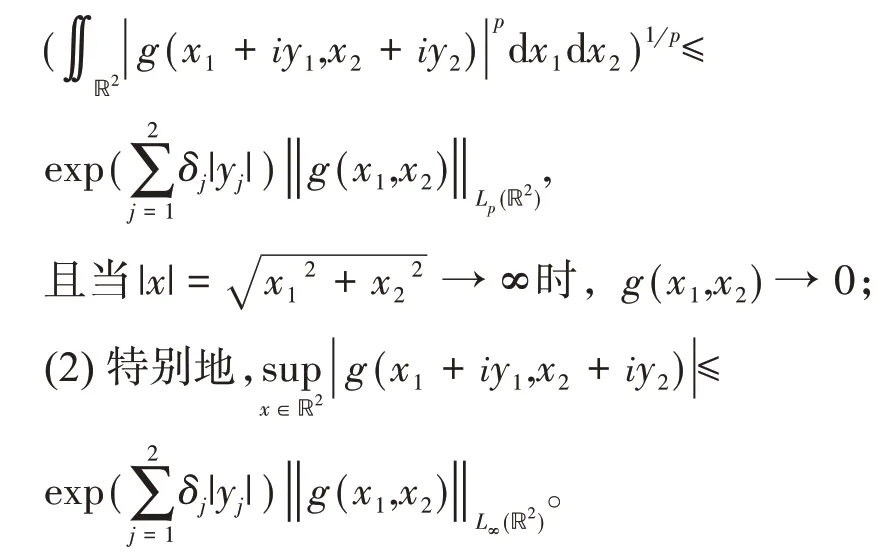
引理2设f(z1,z2)，(z1,z2)∈ℂ2为指数型整函数，且对任意(k1,k2)∈ℤ2，都有f(k1,k2)=0。则存在指数型整函数φ(z1,z2)，使得

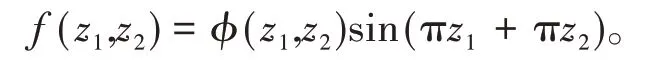
证明设f(z1,z2)为指数型δ=(δ1,δ2)整函数。那么对任意ε＞0，存在常数A＞0，使得对所有(z1,z2)∈ℂ2，都有

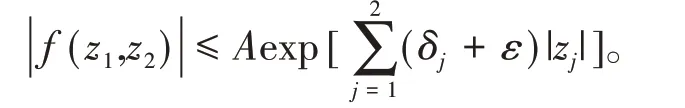
设zj=xj+iyj，xj,yj∈ℝ，j=1,2。不妨取m∈ℤ+。记Cm是以|xj|=m+1/2，|yj|=m+1/2，j=1,2 为边界的方体面。于是在Cm及其内部有

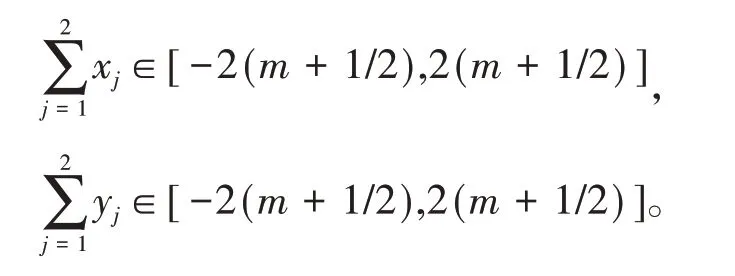
当(z1,z2)属于Cm时，有|sin(πz1+πz2)|≥1，从而

由极大模原理，当(z1,z2)属于Cm的内部时，有

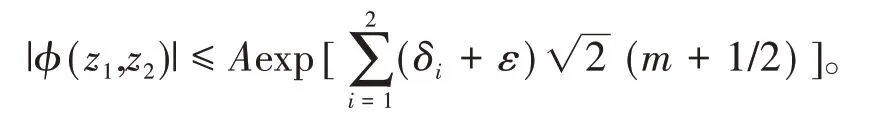
特别地，当|zj|≤m+1/2，j=1,2时，有

证毕。

由于f(z1,z2)为指数型整函数且f(k1,k2)=0，所以由引理2，存在指数型整函数φ1(z1,z2)，使得

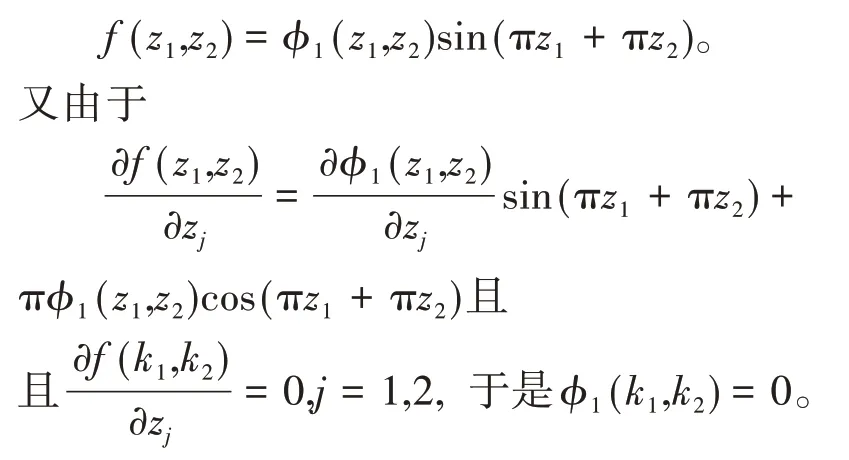
由引理2知，存在指数型整函数φ2(z1,z2)，使得

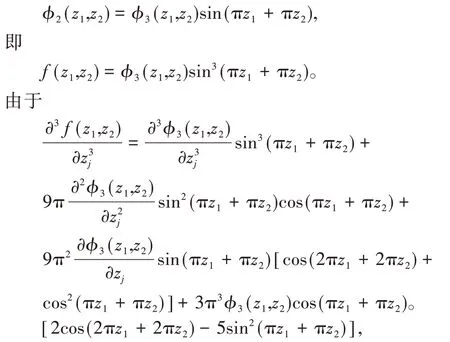
令φ(z1,z2)=φ4(z1,z2)，定理得证。证毕。

设(z1,z2)∈ℂ2。由定理2，存在指数型整函数φ(z1,z2)，使得

(1)若f(x1,x2)∈Bσ,∞(ℝ2)。因为f(z1,z2)为指数型σ=(4π,4π)整函数，所以由引理1(2)，有

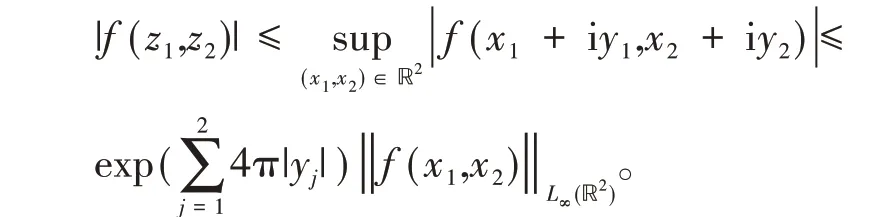
由于当(z1,z2)属于Cm时，存在常数A＞0，使得

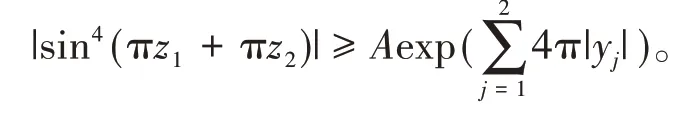
因此当(z1,z2)属于Cm时，

由极大模原理，当(z1,z2)属于Cm的内部，有

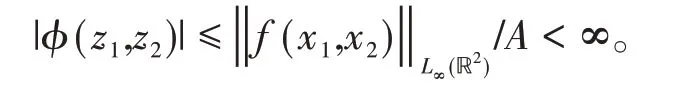
从而由m的任意性，对任意(z1,z2) ∈ℂ2，φ(z1,z2)有界。由刘维尔定理，存在常数C，使得φ(z1,z2)=C，即

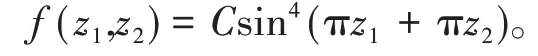
(2) 若f(x1,x2)∈Bσ,p(ℝ2)，1 ≤p＜∞。由 于Lp(ℝ2)⊂L∞(ℝ2)，所以上面的等式成立。由引理1(1)，当时，f(x1,x2) →0，从而C≡0，即f(x1,x2)≡0。

证毕。

3 结语

利用多元复分析的方法，得到了二元指数型整函数的Carlson定理。该定理在二元函数的逼近问题中具有非常重要的作用，特别地对在所有整数点处的函数值、一阶偏导数值、二阶偏导数值及三阶偏导数值为零的二元指数型整函数的逼近问题具有重要作用。